Похожие презентации:
Методы классификации и регрессии
1.
oobasov@mail.ru-
1
2.
,.
2
3.
1):
https://docs.google.com/spreadsheets/d/1I595ZXYJJRRbGFpuLN0XGn7DzljadTXXvbFIiRfpW8/edit?usp=sharing
:
https://docs.google.com/spreadsheets/d/1df7pT164xMzcvrCfX3iC7kVFRaz1J3i
qzD2OK468Nrs/edit#gid=2109442725
1)
1)
:
:
https://docs.google.com/document/d/1LeOOz9jsPRm2fuYQEtjc_8gxIxOrCoEcDSlvlPqZYY/edit?usp=sharing
3
4.
Jonathan T. Barron (2019). A General and Adaptive Robust Loss Function. // https://arxiv.org/pdf/1701.03077.pdf.
Jaderberg, M. et. al (2016). Decoupled Neural Interfaces using Synthetic Gradients. // Arxiv.org
Diederik P. Kingma and Jimmy Ba (2014). Adam: A Method for Stochastic Optimization. // https://arxiv.org/abs/1412.6980.
Davis J., Goadrich M. (2006). The Relationship Between Precision-Recall and ROC Curves. // Proceedings of the 23rd
International Conference on Machine Learning, Pittsburgh, PA.
Mohri, M., Rostamizadeh, A., Talwalkar, A. Foundations of Machine Learning. // MIT Press, 2012
.
.
.
.
//
http://www.
recognition.mccme.ru/pub/RecognitionLab.html/slbook.pdf
Tai, Farbound and Lin, Hsuan-Tien. Multilabel Classification with Principal Label Space Transformation. // Neural
Comput., 24-9, 2012.
. .
. //
.
. .
. 2014.
Hastie T., Tibshirani R., Friedman J. (2009). The Elements of Statistical Learning.
Hastie, T., Tibshirani, R., Friedman, J. (2001). The Elements of Statistical Learning. // Springer, New York.
Domingos, Pedro (2000). A Unified Bias-Variance Decomposition and its Applications. // In Proc. 17th International Conf.
on Machine Learning.
Breiman, Leo (2001). Random Forests. // Machine Learning, 45(1), 5 32.
Friedman, Jerome H. (2001). Greedy Function Approximation: A Gradient Boosting Machine. // Annals of Statistics, 29(5),
p. 1189 1232.
Gulin,
A.,
Karpovich,
P.
(2009).
Greedy
function
optimization
in
learning
to
rank.
http://romip.ru/russir2009/slides/yandex/lecture.pdf
Tianqi Chen, Carlos Guestrin (2016). XGBoost: A Scalable Tree Boosting System. // http://arxiv.org/abs/1603.02754
4
5.
I.II.
III.
IV.
V.
VI.
VII.
5
6.
.:
,
.
.
:
,
.
.
6
7.
x,.
X.
,
. .
Y.
: Y = R.
y.
7
8.
.X = {(x1, y1), . . . , (x , y )},
,
x1, . . . , x
.
,
y1, . . . , y .
8
9.
.x
-
.
:
(set-valued,
.
9
10.
:1. Y = {0, 1}
.
.
2. Y = {1, . . . , K}
(multi-class)
.
3. Y = {0, 1}K
classification).
4.
. .).
(multi-label
.
(semi-supervised learning)
.
.
10
11.
:1.
.
.
2.
.
.
11
12.
:3.
.
4.
.
.
.
12
13.
-X ∈ R ×d (
a:X
Y,
,
d
.
.
.
.
.
.
(mean
squared error, MSE):
L(y, z) = (y-z)2).
L : Y×Y
R+
.
13
14.
A,.
a(x).
,
w0):
xi
i-
x.
14
15.
MSE:xij
a(x)
.
j-
i-
.
w,
.
;
.
15
16.
.:
.
.
-
-
.
-
.
.
,
.
,
.
16
17.
(overfitting):
: A = {a : X
Y}.
:
.
контроля сложности семейства алгоритмов
.
17
18.
:1.
;
2.
;
3.
;
4.
;
5.
6.
;
;
7.
18
19.
1920.
:(bias).
wj .
w
:
w = (w1, . . . , wd)
.
(d+1)-
:
.
w0
20
21.
2122.
-.
1.
.
.
m
fj(x)
b1(x), . . . , bm(x),
:
one-hot
.
C = {c1, . . . , cm}.
.
22
23.
b1(x), . . . , bm(x)f(x)),
:
:
c1
w1),
one-hot
.
23
24.
2.(bag of words).
bj(x)
m
b1(x), . . . , bm(x),
cj
cj
: {c1, . . . , cm}.
.
:
wj .
24
25.
3.xj
{t1, . . . , tm}.
t0 = -
tm+1 = + .
.
.
25
26.
2627.
.1.
MSE
y
,
L(y, a)
a
.
.
R2
:
MSE):
(mean squared error,
27
28.
.(root mean squared error,
RMSE):
.
R2):
y¯ = 1 P i=1 yi
.
.
28
29.
2. MAE:
(mean absolute error,
MAE):
.
.
29
30.
a2(x)a1(x)
MAE
MSE.
30
31.
y1, . . . , yMSE
:
.
31
32.
MAE::
.
32
33.
:.
.
33
34.
3. Huber loss.
δ
:
,
.
(a - y)
δ,
,
.
δ
δ
0
.
.
,
34
35.
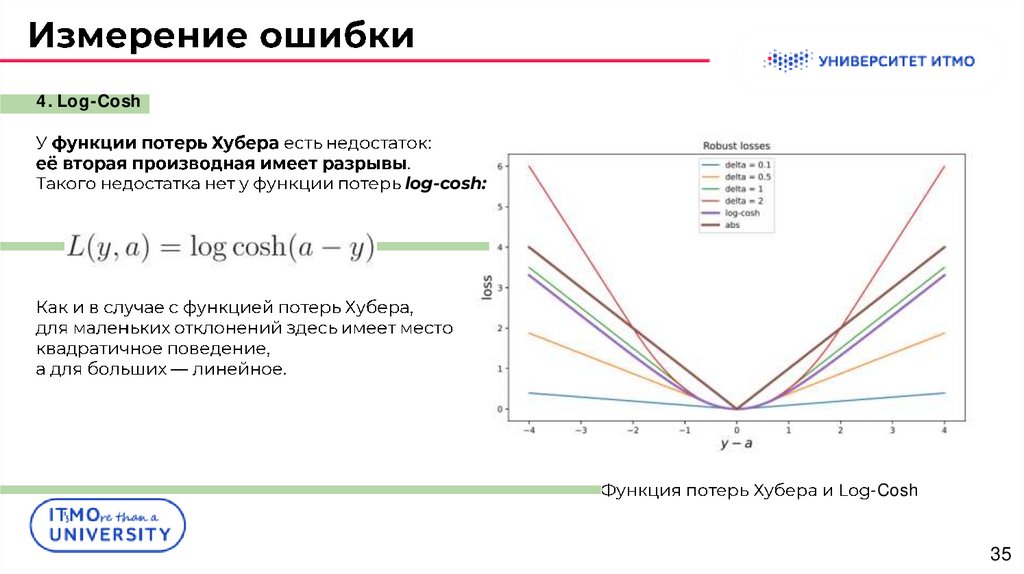
4. Log-Cosh:
.
log-cosh:
.
-Cosh
35
36.
5. MSLE:
(mean
squared logarithmic error, MSLE).
.
.
,
36
37.
6. MAPESMAPE
:
1.
2.
:
-
-
.
.
:
absolute percentage error, MAPE).
(mean
37
38.
MAPE.
:
y = 1
(a < y)
,
,
(a > y)
(symmetric mean absolute percentage error, SMAPE)
37 38
39.
7.:
-
,
.
.
:
[0, 1]
τ
.
τ,
.
39
40.
p(y | x)x∈X
.
:
может возникать в задаче предсказания кликов по рекламным баннерам: один и тот же
пользователь может много раз заходить на один и тот же сайт и видеть данный баннер. При этом
некоторые посещения закончатся кликом, а некоторые — нет.
1)
2)
: a(x)
: a(x)
median[p(y | x)].
a(x)
E[y | x];
,
40
41.
1.2.
x
q,
1.
p(y | x).
:
:
1.
:
q
τ-
τρτ(z)
p(y | x).
.
a(x)
41
42.
4243.
..
:
Существует некоторая одномерная выборка, значения единственного признака x в которой
генерируются равномерно на отрезке [0, 1], а значения целевой переменной выбираются по
формуле y = cos(1.5πx) + N (0, 0.01),
где N (µ, σ2) — нормальное распределение со средним µ и дисперсией σ2.
Возможно восстановить зависимость с помощью линейных моделей над тремя наборами
признаков: {x}, {x, x2, x3, x4} и {x, x2, . . . , x15}.
43
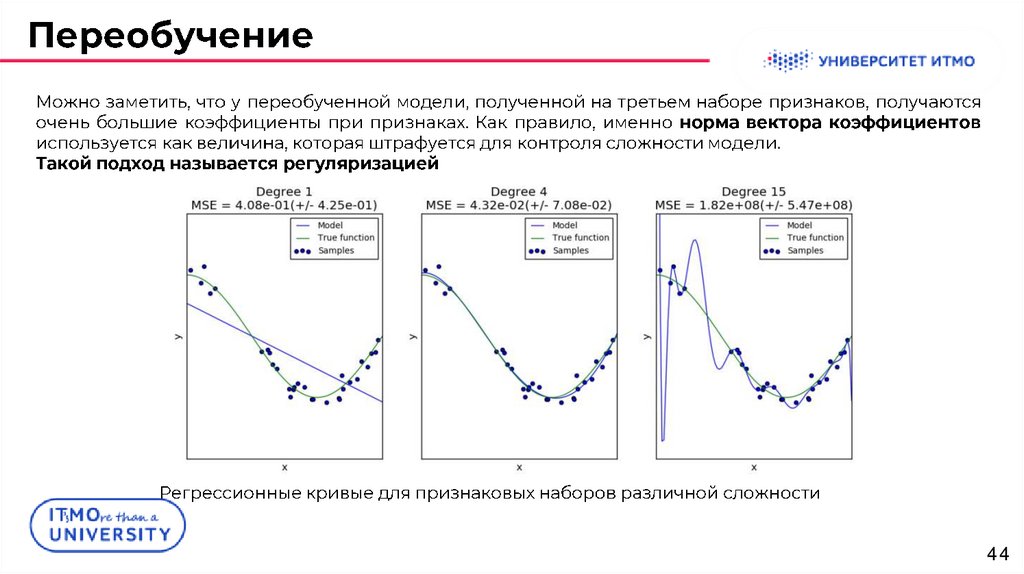
44.
..
44
45.
4546.
.1)
2)
!!!
-
-
.
;
:
.
. .
.
.
46
47.
:.
:
1)
2)
3)
k
i;
k
a1(x), . . . , ak(x),
X1, . . . , Xk
i-
;
:
47
48.
Как получить финальную модель для дальнейшего использования?1.
;
1.
a1(x), . . . , ak(x),
-
.
.
48
49.
4950.
.:
X
-
L2-
y
.
.
w
,
:
w,
50
51.
:1)
;
1)
XT X
.
:
.
MSE
.
.
.
51
52.
51 5253.
.f : Rd
R
:
:
Известно, что градиент является направлением наискорейшего роста функции, а антиградиент
(т.е. -∇f) — направлением наискорейшего убывания.
,
.
53
54.
v ∈ Rdx0 ∈ Rd
:
: ||v|| = 1.
.
x0
v
:
54
55.
::
v.
ϕ
,
,
180
,
.
.
55
56.
:У градиента есть ещё одно свойство - он ортогонален линиям уровня.
x0
S(x0) = {x ∈ Rd | f(x) = f(x0)}
1.
.
x0:
x0 + ε ∈ S(x0).
f(x0 + ε) = f(x0)
-
:
||ε||:
1.
||ε||
1.
x 0.
.
ε/||ε||
.
56
57.
:Основное свойство антиградиента — он указывает в сторону наискорейшего убывания функции в
данной точке.
w(0)
:
Q(w)
ηk
w.
.
: ηk = c.
:
57
58.
1)2)
(||∇Q(w(k-1)|| < ε);
:
(||w(k) - w(k-1)|| < ε).
:
следить за ошибкой модели на отложенной выборке и останавливаться, если эта ошибка
перестала убывать.
-
:
если функция выпуклая и дифференцируемая, для её первой производной выполнено
условие Липшица, длина шага выбрана правильно, то градиентный спуск сойдётся к
минимуму функции;
также имеет место следующая оценка сходимости для градиентного спуска:
.
58
59.
Q(w):
:
.
.
59
60.
1.:
ik
.
(stochastic gradient descent,
SGD).
.
,
:
.
60
61.
SGD.
SGD
.
1),
-
:
:
61
62.
.,
n
ikj
:
(j
1
n),
.
.
mini-batch gradient descent,
62
63.
2.SAG
(stochastic average gradient)
.
1)
1)
w 0,
zi0,
k-
:
:
ik
63
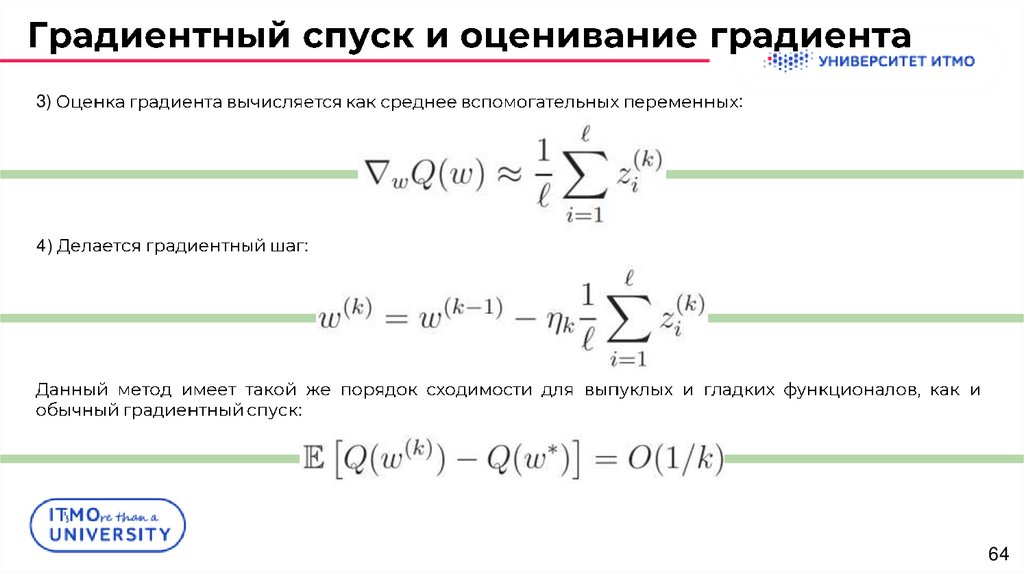
64.
3):
4)
:
:
64
65.
SAG.
.
:
i-
.
qi (〈w, xi〉)
65
66.
3.-
-
-
u
:
∇wqi(w)
.
66
67.
6768.
v,w +αv
w
x
〈v, x〉 = 0.
.
точно такие же ответы
68
69.
,:
.
αw0 L2
L1-
:
69
70.
L2-.
:
.
:
L2
XTX
.
70
71.
7172.
.-
-
.
.
:
введение регуляризации мешает модели подгоняться под обучающие данные, и с точки
зрения среднеквадратичной ошибки выгодно всегда брать α = 0.
выборку, на которой настраиваются гиперпараметры, называют валидационной, и при этом
выделяют третий, тестовый набор данных, на которых оценивается качество итоговой
модели.
72
73.
7374.
:Модели, в которых некоторые веса равны нулю, называют разреженными, поскольку прогноз в них
зависит лишь от части признаков.
Пример:
1. Может быть заведомо известно, что релевантными являются не все признаки. Очевидно, что
признаки, которые не имеют отношения к задаче, надо исключать из данных, то есть
производить отбор признаков (L1-регуляризация);
1.
К модели могут выдвигаться ограничения по скорости построения предсказаний (L1регуляризация);
1.
В обучающей выборке объектов может быть существенно меньше, чем признаков (так
называемая «проблема N ≪ p») (L1-регуляризация).
74
75.
1.Q(w) + α||w||1
Q(w)
C:
Q(w) -
||w||1
-
-
75
76.
2.w = (1, ε),
.
L1-
ε
δ < ε:
L2-
:
2-
76
77.
3..
L1-
F(w) = ||Xw - y||2
:
η
,α
Sηα(w)
77
78.
7879.
1.:
:
:
-
log xj
-
exp(||x -
-
sin(xj/T )
2/σ)
79
80.
2.-
.
1
f1(x) = ½*x21+ ½*x22
x(0) = (1, 1)
1)
2)
3)
η=1
:
2
1)
:
f2(x) = 50x21 + ½*x22
x(0) = (1, 1)
1)
:
(-100, -1)
.
80
81.
1)1)
:
[0, 1]:
81
82.
8283.
X = RdY = {-1, +1}
X = {(xi, yi)} i=1
.
:
w ∈ Rd
w0 ∈ R
(bias)
xd+1 = 1.
w 0,
〈 w, x〉-
83
84.
1.(accuracy):
:
-
⇒
84
85.
1..
Mi = yi 〈w, xi 〉,
:
〈w,
;
xi
(margin)
〉
85
86.
1..
L(M) = [M < 0],
x
M = y〈w, xi 〉.
1)
1)
.
.
86
87.
1..
1)
2)
= log (1 + e-M )
= (1 - M)+ = max(0, 1 - M)
1)
= (-M)+ = max(0, -M)
1)
2)
= e-M
= 2/(1 + eM)
-
.
87
88.
8889.
.a(x) = sign(b(x)-t) = 2[b(x) > t] - 1.
b(x) = 〈w, x 〉
t = 0.
1.
Пример: если в выборке 950 отрицательных и 50 положительных объектов, то при тривиальном
пороге t = maxi b(xi) мы получим долю правильных ответов 0.95.
Это означает, что доля положительных ответов сама по себе не несет никакой информации о
качестве работы алгоритма a(x), и вместе с ней следует анализировать соотношение классов в
выборке.
Важно: также полезно вместе с долей правильных ответов вычислять базовую долю — долю
правильных ответов алгоритма, всегда выдающего наиболее мощный класс.
89
90.
.1.
a1
r1.
-
a2
a2
20%
50%
90%.
10%,
25%,
0.1%
.
0.01%,
r1
r2
:
r2 >
50%.
50%,
90
91.
.2.
-
91
92.
.2.
:
y=1
y = -1
.
.⇒
a(x) = sign(b(x) - t) = 2[b(x) > t] - 1.
a(x)
1.
t
:
92
93.
.2.
F-
precision ≪ 1,
:
1/2,
.
recall = 1
93
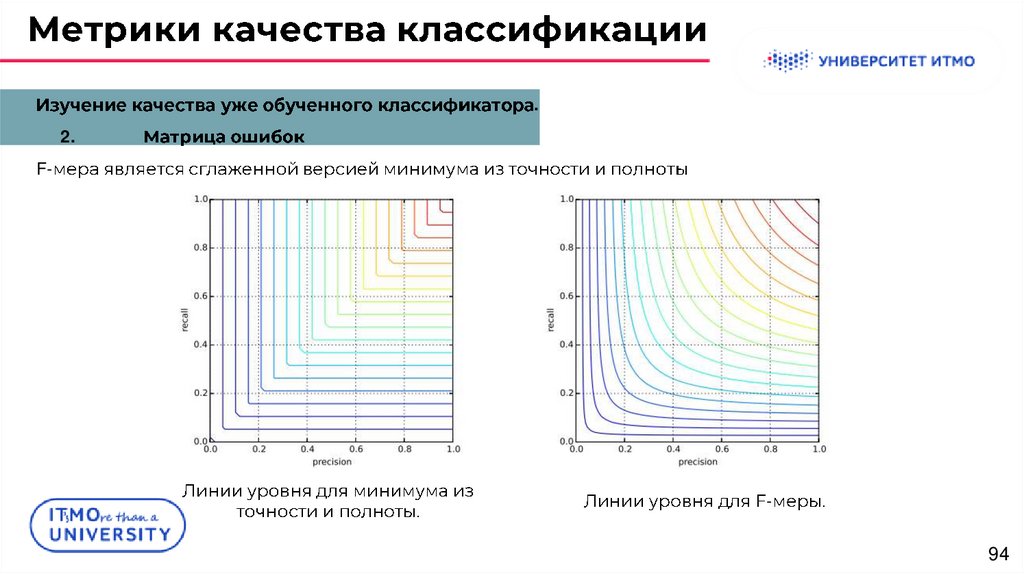
94.
.2.
F-
-
94
95.
.2.
R-
(breakeven point).
:
t,
R.
95
96.
.2.
b(x),
b(x).
t,
precision, AP):
y(k)
(average
k-
+
precision@k
k
.
96
97.
.2.
:
1% ( + = 10.000).
10.000
9.000
1000.
( = 1.000.000),
TP = 9000, FN = 1000.
.
90%
90%,
FP =
(1 - 2.000/1.000.000) = 99.8%!
97
98.
.2.
Lift -
:
.
98
99.
.3.
Area Under Curve
.
{a(x) = sign(b(x) - t)
| t ∈ R}.
ROC-
Under ROC Curve, AUC-ROC):
FPR
TPR
b(x),
(Area
(False Positive Rate),
(True Positive Rate).
99
100.
.3.
Area Under Curve
-
TPR = 0, FPR = 0.
ROC-
+ 1.
tmax = maxi b(xi)
tmin = mini b(xi) - ε
TPR = 1
(0, 0)
FPR = 1.
(1, 1),
b(x(1))- ε, b(x(1)), b(x(2)), . . . , b(x( )).
-
- AUC-ROC,
t
AUC-ROC
b(x)
0
1.
AUC-ROC
0.5.
a(x)
;
,
100
101.
.3.
Area Under Curve
(Gini index) -
.
AUC-ROC
Gini = 2AUC - 1.
-
ROC:
(0, 0)
(1, 1).
AUC
101
102.
.3.
Area Under Curve
.
1)
:
.
1.000.100
a(x),
1)
0.95
FPR = 0.05,
100
.
.
TPR
95
.
FPR
50.000
TPR =
:
если положительный класс существенно меньше по размеру, то AUC-ROC может давать
неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых
объектов относительно общего числа отрицательных.
102
103.
.3.
Area Under Curve
Precison-recall
FPR TPR,
-
ROC-
.
PR-
:
1.
2.
k
k
1.
PR-
(0, 1)
-1
1
k
precision@k
1/ +
:
ROC-
PR-
(AUC-PR).
.
ROC-
103
104.
104105.
.x∈X
+1.
p(y = +1 | x)
x
x
p(y = +1 | x).
b(x)
p(y = +1 | x).
x
[0, 1].
n
x
{y1, . . . , yn},
:
105
106.
n:
L(y, z) = (y - z)2,
y = 1,
L(y, x) = |y - z|.
y = 0.
,
1000
b:
1/10:
106
107.
.b(x) = 0,
: (1 - 0)2 = 1.
.
b(x) ∈ [0, 1]
b(xi)[yi=+1](1-b(xi))[yi=-1].
:
.
:
xi
yi,
(log-loss)
107
108.
.1.
2.
3.
.
x:
b:
:
:
108
109.
.1.
b(x) = σ(hw, xi),
σ
[0, 1]
1.
1.
〈w, x〉
1.
1.
-odds):
109
110.
.:
.
.
110
111.
111112.
:.1.
w∗
a(x) = sign(〈w, x〉 + b)
b∗,
.
a(x)
.
:
x0 ∈ Rd
112
113.
1.(margin).
2/||w||.
113
114.
1..
(hard margin support vector machine):
yi(〈w, xi〉 + b) > 0.
xi
yi(〈w, xi〉 + b) > 1.
114
115.
2.:
w
:
ξi > 0
:
ξ > 0.
(0
b
:
yi (ㄑw, xi〉 + b) < 1),
.
115
116.
2.1/||w||
(soft margin).
,
C
i=1 ξi.
-
.
:
.
(soft margin support vector machine).
116
117.
3.1)
1)
:
:
ξi
1)
.115):
L(y, z) = max(0, 1 - yz)
117
118.
118119.
K: Y = {1, . . . , K}.
1.
(one-versus-all)
1)
K
1, . . . , K
.
k-
k
b1(x), . . . , bK(x),
.
(xi, 2[yi = k] - 1) i=1;
:
119
120.
K: Y = {1, . . . , K}.
1.
(one-versus-all)
.
b1(x), . . . , bK(x)
-
120
121.
K: Y = {1, . . . , K}.
1.
1)
1)
CK2
(all-versus-all)
aij(x), i, j = = 1, . . . , K, i
aij(x)
aij(x)
j.
:
Xij ⊂ X,
i
i,
j:
j.
1)
121
122.
K: Y = {1, . . . , K}.
2.
.
1)
K
1)
1)
SoftMax(z1, . . . , zK),
bk(x) = 〈wk, xi 〉 + w0k,
.
:
k-
122
123.
K: Y = {1, . . . , K}.
2.
:
123
124.
b.3.
1)
K
w1, . . . , wK,
1)
:
:
k = y(x),
〈wk, xi〉
k = y(x);
〈wk, xi〉 + 1.
.
124
125.
3.k-
wk:
W,
125
126.
3..
1)
:
:
SVMmulticlass
:
.
126
127.
4.1)
2)
:
-
.
1)
2)
kTPk, FPk, FNk, TNk)
yik = [yi = k].
(TP, FP,
. .)
F-
ak(x) = [a(x) = k]
.
TP
127
128.
4.1)
2)
:
-
.
.
:
.
-
,
,
TP, FP, FN
TN
.
128
129.
129130.
Kx
;
yik
.
.
y ∈ {0, 1}K,
X
xi
Y ∈ {0, 1} ×K,
k (multi-label classification).
130
131.
1.(Binary relevance)
-
K
(xi, yik) i=1.
:
x
a1(x), . . . , aK(x),
bk(x)
(a1(x), . . . , aK(x))
.
:
-
.
131
132.
2.-
1)
2)
3)
X
K
:
2
1)
X1
xi ∈ X2
X2.
b1(x), . . . , bK(x)
a1(x ), . . . , aK(x ),
b1(x), . . . , bK(x).
.
132
133.
2.:
bk(x) ak(x)
bk(x)
x ik = bk(xi),
X1;
.
:
b(x)
5%,
10%
-
.
a(x)
5%,
.
133
134.
3.-
.
Y:
-
1)
Σ
m.
VM
.
2)
1)
2)
3)
m
Y
M
Y:
Y
A
V,
:
a1(x), . . . , aM(x)
A ∈ R ×M.
134
135.
4.Zi
Yi
xi
a(x).
:
135
136.
4.:
.
136
137.
137138.
f(x).U = {u1, . . . , un}.
1.
x
(one-hot encoding)
1)
n
2)
.
n
:
g1(x), . . . , gn(x),
.
138
139.
f(x).U = {u1, . . . , un}.
x
2.
1)
2)
1)
2)
-
1
h : U
B
{1, 2, . . . , B},
-
:
.
B < |U|)
.
139
140.
f(x).U = {u1, . . . , un}.
x
3.
:
.
1)
ui
u
uj
(K + 1)
:
140
141.
3.2)
-
f(x)
ck -
gk(x)
K
g1(x), . . . , gK(x):
p(y = k | f(x))
X
.
: gk(x)
.
m
X1, . . . , Xm,
:
Xi
.
141
142.
3.-
1)
2)
3)
successes(u, X)
.
gk(x),
fi(x)
fj(x)
counts(f(x), X)
. .
fij(x) = = (fi(x), fj(x)).
h(u).
4)
5)
counts(u, X),
successesk(f(x), X).
u ∈ U,
c1, . . . , cK.
.
:
142
143.
143144.
:1.
2.
3.
4.
.
:
10
:
:
18,
50
.
3,
.
.
4.
.
.
144
145.
.-
:
v,
v
cv ∈ Y
:
a(x),
-
βv : X
{0, 1}
v0
βv0:
.
.
.
145
146.
.βv,
:
-
βv(x) = [〈w, x〉 < t];
βv(x) = [ρ(x, xv) < t],
.
:
xv
:)
-
146
147.
147148.
.1)
2)
X
R1(j, t) = {x | xj < t}
Q(X, j, t).
3)
j
R2(j, t) = {x | xj > t}
t,
[xj < t].
.
1)
2)
3)
4)
.
(pruning)
.
:
148
149.
.:
1.
;
2.
Q(X, j, t);
3.
;
4.
5.
;
.
149
150.
150151.
:.
:
- Rm .
R
Rr
H(R)
(impurity criterion)
L(y, c)
151
152.
1.:
:
:
.
152
153.
2.pk
k∗
k (k ∈ {1, . . . , K}),
R:
: k∗ = arg max k pk
153
154.
2..
:
-
:
.
k∗
:
pk∗
154
155.
2..
:
c = (c1, . . . , cK),
K
k=1 ck = 1.
(Brier score):
pk:
155
156.
2..
:
- ck
.
:
:
ck = pk/λ.
k,
156
157.
2..
ck = pk
:
:
:
:
157
158.
158159.
:.
.
.
.
s
:
-
.
.
159
160.
160161.
,.
-
.
161
162.
Cost-complexity pruning.T0
Rα(T) -
|T|
-
:
R(T)
R(T)
T,
α>0
,
.
.
:
TK
T0
Ti
α
0 = α0 < α
α ∈ [αi, αi+1),
αK <
162
163.
163164.
.1.
:
β(x) = [xj < t],
R
j
j V
1)
1)
2)
3)
Vj
|R |/|R|
.
|Rr|/|R|
.
.
[yi = k]
164
165.
.k
:
2.
-
Rm
amk(x),
.
-
:
.
165
166.
166167.
:xj
Q = {u1, . . . , uq}, |Q| = q
1)
2)
: Q = Q1⊔Q2
: β(x) = [xj ∈ Q1]
:
.
1)
2)
3)
2q-1 - 1
Rm(u)
Nm(u)
u;
,
m
j-
.
+1:
167
168.
:4)
xj
Q = {u1, . . . , uq}, |Q| = q
u(i)
MSE-
i,
:
168
169.
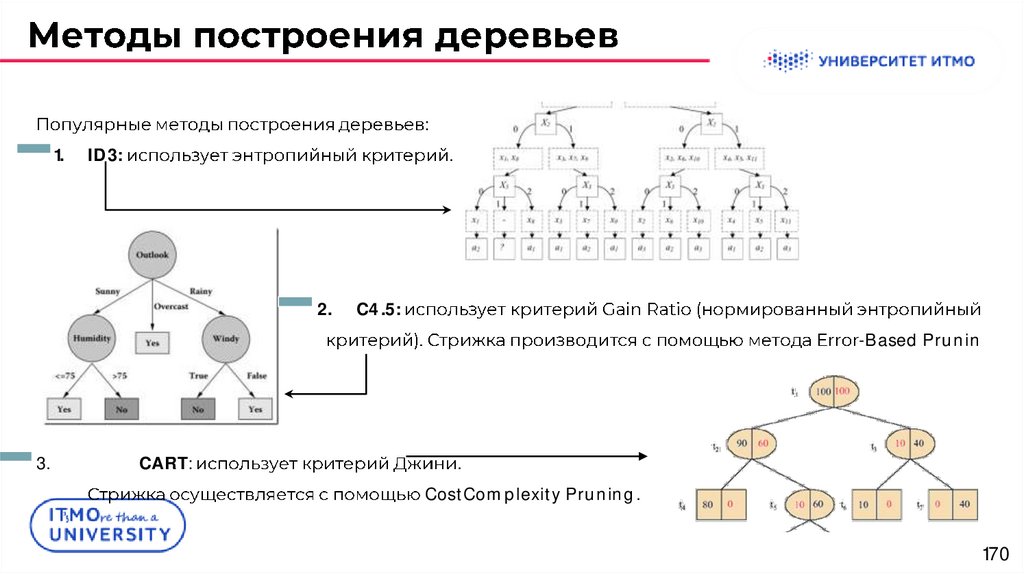
169170.
:1.
ID3:
.
2.
C4.5:
-Based Prunin
3.
CART:
.
CostComplexity Pruning.
170
171.
171172.
a(x)wj .
{J1, . . . , Jn},
Jj
([x ∈ Jj])nj=1
:
:
.
172
173.
Bias-Variance decomposition-
,
173
174.
:1)
2)
3)
4)
5)
6)
X = (xi, yi)
.
N
N
.
X1.
.
X1, . . . , XN.
b1(x), . . . ,
bN(x)
p(x),
:
:
y(x),
174
175.
7)8)
175
176.
9):
N
176
177.
Bias-Variance decomposition177
178.
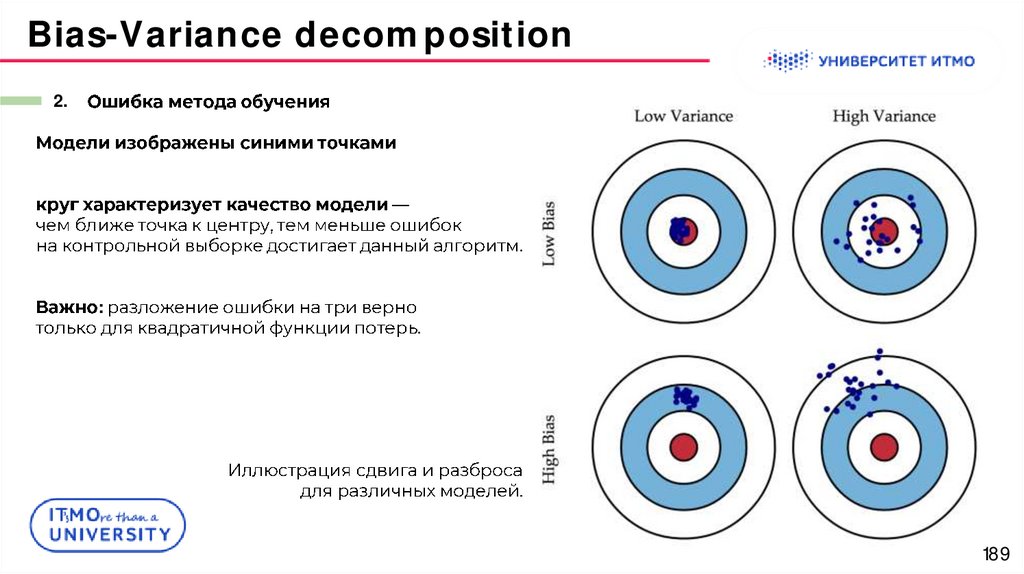
Bias-Variance decomposition:
1.
2.
3.
,
,
.
.
:
X = (xi, yi) i=1
:
yi ∈ R
X
.
X × Y
p(x, y),
178
179.
Bias-Variance decomposition:
p(x, y).
y,
(x, y),
x
179
180.
Bias-Variance decomposition1.
:
1)
:
180
181.
Bias-Variance decomposition1.
2)
:
:)
3)
Ex,y[f(x, y)]
:
181
182.
Bias-Variance decomposition1.
4)
5)
y:
E(y | x)-a(x)
y,
:
182
183.
Bias-Variance decomposition1.
a(x)
a(x) = E(y | x).
:
Ex,y(E(y | x) - a(x))2,
.
183
184.
Bias-Variance decomposition2.
:
:
p(x, y).
: (X ×Y)
A,
A.
:
i=1 p(xi, yi)
EX
{(x1, y1), . . . , (x , y )}
184
185.
Bias-Variance decomposition2.
:
.
X
,
X
:
185
186.
Bias-Variance decomposition2.
:
186
187.
Bias-Variance decomposition2.
::
187
188.
Bias-Variance decomposition2.
:
(bias)
.
.
.
(variance),
188
189.
Bias-Variance decomposition2.
.
:
.
189
190.
Bias-Variance decomposition190
191.
:.
:
:
,
=
.
(bagging, bootstrap aggregation)
,
Alarm!
bn(x)
:
.
,
.
X,
191
192.
:>
>
192
193.
.:
:
193
194.
.X:
N
.
.
194
195.
1.-
.
:
1)
2)
.
-
.
d
.
m=⌊
⌋,
.
m = ⌊d/3⌋,
195
196.
1.. Out-of-Bag
:
Xn
xi
xi
out-of-bag-
L(y, z)
bn
:
.
N
.
leave-one-out-
,
196
197.
1..
.
Tn(x)
Tn(x).
n-
x.
x
197
198.
1..
:
.
k
:
.
Tn(x),
.
.
198
199.
Extreme Gradient Boosting (XGBoost)199
200.
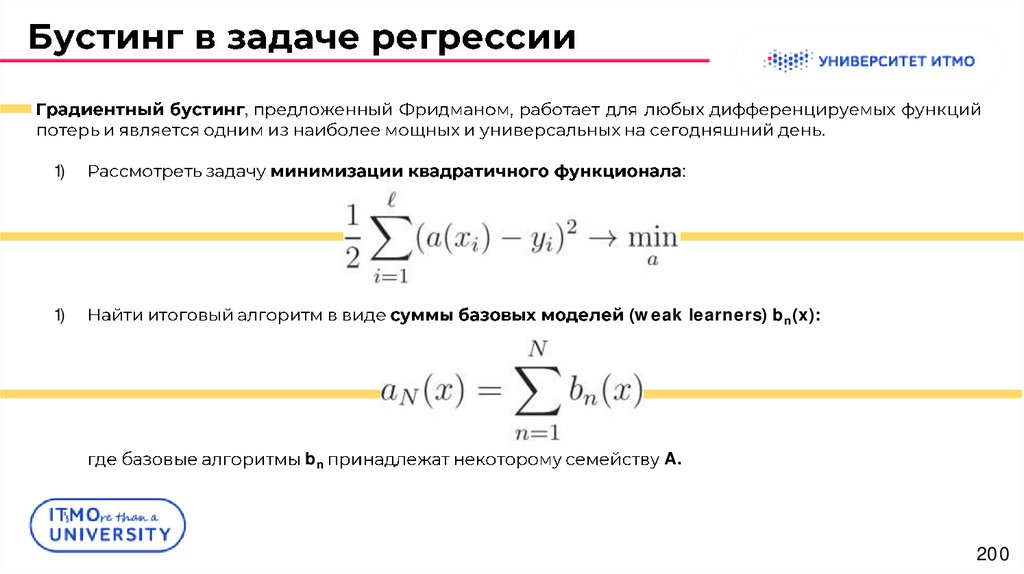
,.
1)
:
1)
(weak learners) bn(x):
bn
A.
200
201.
3)4)
5)
:
:
:
201
202.
6):
:
.
202
203.
Extreme Gradient Boosting (XGBoost)203
204.
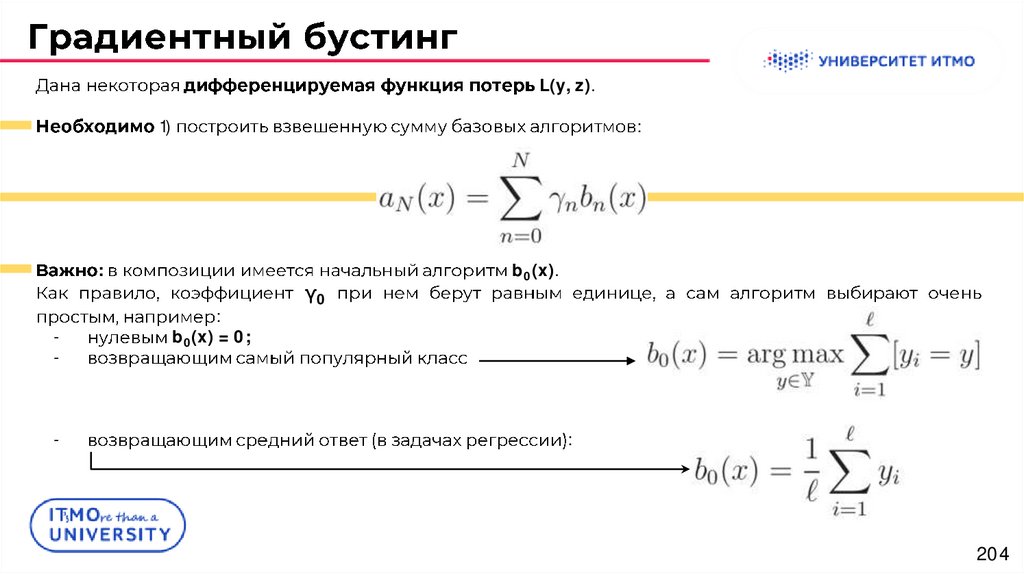
L(y, z).1)
:
:
-
-
:
b0(x) = 0;
γ0
b0(x).
:
204
205.
2)3)
*
bN (x)
s1 , . . . , sl
si = yi
aN
:
1(xi ),
z = aN 1 (xi ):
si
205
206.
:s = (s1 , . . . , sl )
.
:
si(N) ,
.
4)
.
:
206
207.
-5)
:
l
.
(si)i );
.
:
207
208.
Extreme Gradient Boosting (XGBoost)208
209.
.-
η ∈ (0, 1]
Xk ⊂ X.
:
bN
X,
209
210.
Extreme Gradient Boosting (XGBoost)210
211.
1.1.
:
211
212.
2.N-
yiaN
:
1 (xi )
i-
.
:
xi
N-
.
212
213.
Extreme Gradient Boosting (XGBoost)213
214.
.:
j = 1, . . . , Jn
Rj
bnj
N-
:
.
:
214
215.
JN-
γN
:
. .
Rj
JN
[x ∈ Rj ].
γN j
.
γN j
JN
bN j
:
215
216.
.:
:
-
γN j = 0.
:
216
217.
Extreme Gradient Boosting (XGBoost)217
218.
AdaBoostL(y, z) = e
)
:
(N
1)-
:
.
(yi)li=1.
218
219.
::
.
219
220.
Extreme Gradient Boosting (XGBoost)220
221.
:-
:
.
:
.
221
222.
,:
1.
1.
-
(N
;
1)-
:
1/2.
222
223.
Extreme Gradient Boosting (XGBoost)223
224.
.Q(w)
H(w)
,
.
si):
:
224
225.
:si
:
s:
:
.
LogitBoost
225
226.
Extreme Gradient Boosting (XGBoost)226
227.
Extreme Gradient Boosting (XGBoost)1.
1)
1)
s:
s:
227
228.
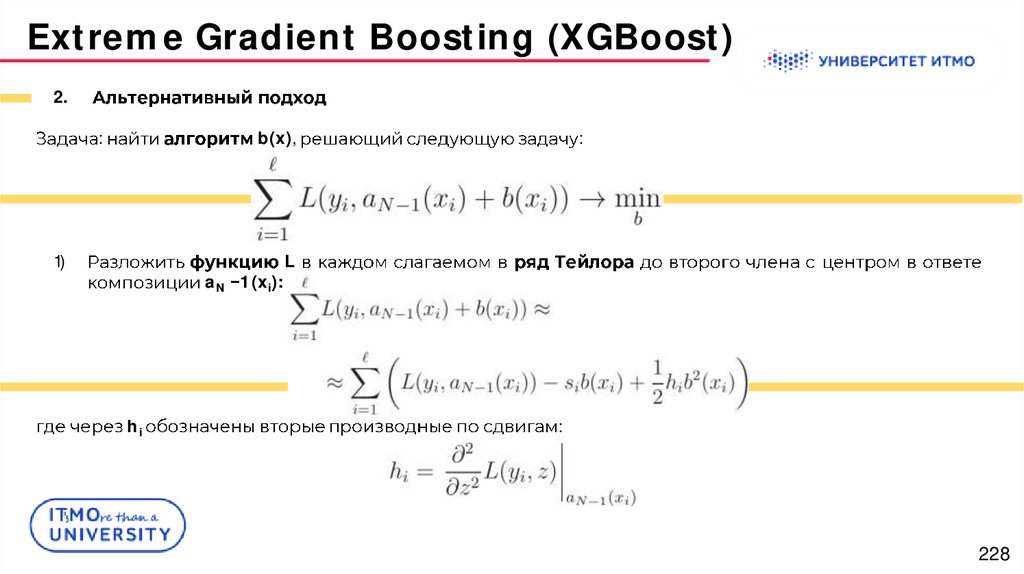
Extreme Gradient Boosting (XGBoost)2.
:
b(x),
1)
aN 1 (xi):
hi
:
L
:
228
229.
Extreme Gradient Boosting (XGBoost)2.
:
b(x),
2)
3)
:
:
:
s.
229
230.
Extreme Gradient Boosting (XGBoost)3.
:
b(x)
:
:
1.
2.
J.
.
||b||22 =
J
j=1
b2j.
.
230
231.
Extreme Gradient Boosting (XGBoost)3.
:
:
:
:
bj ,
231
232.
Extreme Gradient Boosting (XGBoost)4.
[xj < t]
:
.
R
:
Q.
232
233.
Extreme Gradient Boosting (XGBoost)XGBoost
:
1.
.
2.
.
3.
.
4.
.
233
234.
Extreme Gradient Boosting (XGBoost)234
235.
:-
N
a(x).
.
b1(x), . . . , bN(x)
X,
:
-
.
.
-
235
236.
K:
k-
-
X1 , . . . , XK ,
.
.
b
-
j (x)
bj(x),
xi
236
237.
1..
-
:
.
.
w1 =
= wN = 1/N)
237
238.
2..
.
:
-
TF-IDF
-
a(x),
.
238
239.
Jonathan T. Barron (2019). A General and Adaptive Robust Loss Function. // https://arxiv.org/pdf/1701.03077.pdf.
Jaderberg, M. et. al (2016). Decoupled Neural Interfaces using Synthetic Gradients. // Arxiv.org
Diederik P. Kingma and Jimmy Ba (2014). Adam: A Method for Stochastic Optimization. // https://arxiv.org/abs/1412.6980.
Davis J., Goadrich M. (2006). The Relationship Between Precision-Recall and ROC Curves. // Proceedings of the 23rd
International Conference on Machine Learning, Pittsburgh, PA.
Mohri, M., Rostamizadeh, A., Talwalkar, A. Foundations of Machine Learning. // MIT Press, 2012
.
.
.
.
//
http://www.
recognition.mccme.ru/pub/RecognitionLab.html/slbook.pdf
Tai, Farbound and Lin, Hsuan-Tien. Multilabel Classification with Principal Label Space Transformation. // Neural
Comput., 24-9, 2012.
. .
. //
.
. .
. 2014.
Hastie T., Tibshirani R., Friedman J. (2009). The Elements of Statistical Learning.
Hastie, T., Tibshirani, R., Friedman, J. (2001). The Elements of Statistical Learning. // Springer, New York.
Domingos, Pedro (2000). A Unified Bias-Variance Decomposition and its Applications. // In Proc. 17th International Conf.
on Machine Learning.
Breiman, Leo (2001). Random Forests. // Machine Learning, 45(1), 5 32.
Friedman, Jerome H. (2001). Greedy Function Approximation: A Gradient Boosting Machine. // Annals of Statistics, 29(5),
p. 1189 1232.
Gulin,
A.,
Karpovich,
P.
(2009).
Greedy
function
optimization
in
learning
to
rank.
http://romip.ru/russir2009/slides/yandex/lecture.pdf
Tianqi Chen, Carlos Guestrin (2016). XGBoost: A Scalable Tree Boosting System. // http://arxiv.org/abs/1603.02754
239
240.
Спасибо за внимание!www.ifmo.ru
240






































































































































































































































 Математика
Математика








