Похожие презентации:
Сфера, шар и их элементы
1.
2.
РАЗДЕЛ: 11.3А: ТЕЛА ВРАЩЕНИЯ И ИХЭЛЕМЕНТЫ
ТЕМА УРОКА: СФЕРА, ШАР И ИХ ЭЛЕМЕНТЫ
3.
Цели обучения11.1.10 - знать определение сферы, шара;
уметь изображать их на плоскости;
11.3.5 - решать задачи на нахождение
элементов тел вращения (цилиндра, конуса,
усеченного конуса, шара);
4.
В конспект!•сформулируйте определение сферы и ее
элементов;
•сформулируйте определение шара и его
элементов;
5.
Проверь себя (устно)Заполните пропуски
Шар с …….. O и …….. r – это тело, которое является
совокупностью всех …… пространства, находящихся от
центра O на ……….. меньшем или равном r. Шаровой, или
………….. поверхностью (иногда просто сферой) называется
…………………. точек пространства, ………………… от
одной точки – центра шара.
6.
11.3.8 - решать задачи на нахождениеплощади поверхности сферы;
7.
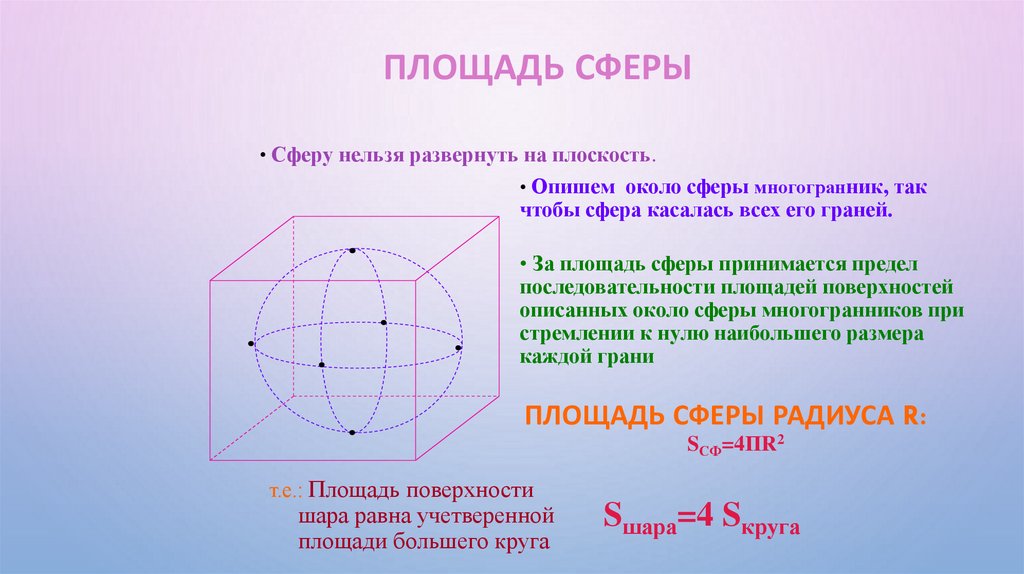
ПЛОЩАДЬ СФЕРЫ• Сферу нельзя развернуть на плоскость.
• Опишем около сферы многогранник, так
чтобы сфера касалась всех его граней.
• За площадь сферы принимается предел
последовательности площадей поверхностей
описанных около сферы многогранников при
стремлении к нулю наибольшего размера
каждой грани
ПЛОЩАДЬ СФЕРЫ РАДИУСА R:
SСФ=4ΠR2
т.е.: Площадь поверхности
шара равна учетверенной
площади большего круга
Sшара=4 Sкруга
8.
УПРАЖНЕНИЕ 1Найдите площадь поверхности шара, вписанного в куб с ребром, равным единице.
Ответ:
.
9.
УПРАЖНЕНИЕ 2Найдите площадь поверхности шара, описанного около куба с ребром, равным
единице.
Ответ:
3 .
10.
УПРАЖНЕНИЕ 4Сечения сферы двумя параллельными плоскостями
имеют длины 36π см и 48π см. Найди площадь
сферы, если расстояние между плоскостями
равно 6 см и центры сечений лежат на одном
радиусе.
Дескриптор: Обучающийся
- верно выполняет чертеж;
- вычисляет радиусы сечений;
- составляет систему уравнений для вычисления
радиуса сферы;
-вычисляет радиус сферы;
-вычисляет площадь поверхности сферы.
11.
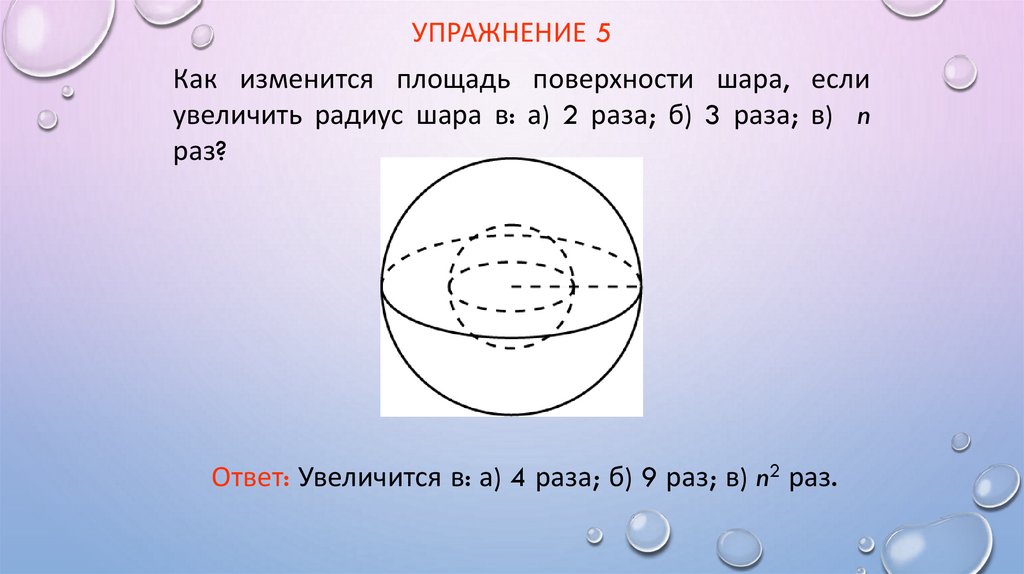
УПРАЖНЕНИЕ 5Как изменится площадь поверхности шара, если
увеличить радиус шара в: а) 2 раза; б) 3 раза; в) n
раз?
Ответ: Увеличится в: а) 4 раза; б) 9 раз; в) n2 раз.
12.
УПРАЖНЕНИЕ 6Радиусы двух параллельных сечений сферы равны 9
см и 12 см. Расстояние между секущими
плоскостями равно 3 см. Найдите площадь сферы.
13.
ОТПРАВИТЬ РЕШЕНИЯ ЗАДАЧ №4,5,6 ДО 13.00НА ПОЧТУ










 Математика
Математика








