Расчет электрических цепей переменного тока (лекция 4)

1. БГТУ «ВОЕНМЕХ» им. Д.Ф. Устинова Кафедра электротехники, О8

Лекция 4
Расчет электрических цепей
переменного тока
1

2.

Представление синусоидальной функции в векторной форме
Рассмотрим вектор длиной Um, который вращается в декартовой системе
координат x-y, против часовой стрелки с угловой скоростью .
y
Um
Um
x
Um
- амплитуда напряжения;
u
- начальная фаза напряжения;
2
2 f
T
- циклическая частота или угловая скорость вращения
вектора напряжения.
2

3.

Имеем узел, где встречаются 3 тока:
i1
i3
Мгновенные значения токов:
i1 (t ) I1m sin( t i1 )
i2 (t ) I 2 m sin( t i 2 )
i2
Для заданного узла составим уравнение на основании первого закона Кирхгофа
i3 (t ) i1 (t ) i3 (t )
В уравнение подставим мгновенные значения токов i1(t) и i2(t) :
i3 (t ) I1m sin( t i1 ) I 2 m sin( t i 2 ) I 3m sin( t i 3 )
Определение амплитуды I3m и 3 начальной фазы этого тока путем
соответствующих тригонометрических преобразований получается
довольно громоздким и мало наглядным.
3

4.

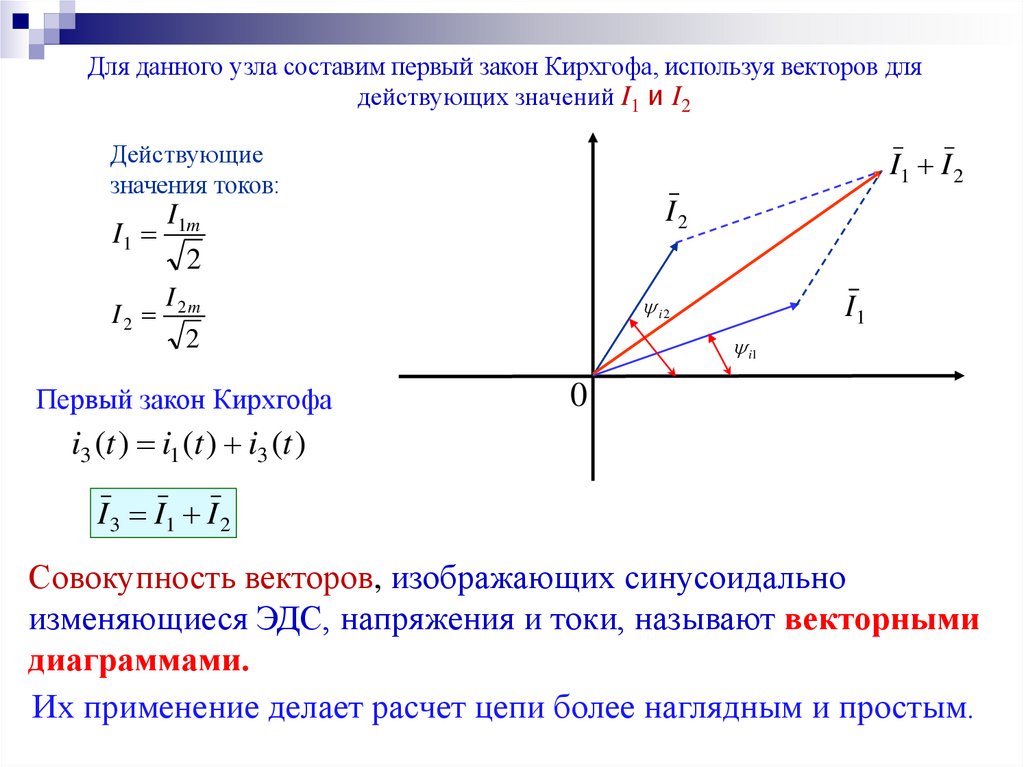
Для данного узла составим первый закон Кирхгофа, используя векторов для
действующих значений I1 и I2
Действующие
значения токов:
I1
I1m
I2
I 2m
I1 I 2
I2
2
i2
2
Первый закон Кирхгофа
I1
i1
0
i3 (t ) i1 (t ) i3 (t )
I 3 I1 I 2
Совокупность векторов, изображающих синусоидально
изменяющиеся ЭДС, напряжения и токи, называют векторными
диаграммами.
Их применение делает расчет цепи более наглядным и простым.

5.

Примеры:
i
Активный элемент
i (t ) I m sin( t i )
I r ( I rm )
ur (t ) i r I m r sin( t i )
U rm sin( t i )
Фазовый сдвиг
ir ur 0
r
ur
U r (U rm )
Ir
Ur
Напряжение на активном элементе совпадает по фазе с током = 0°
Закон Ома
Закон Джоуля -Ленца
U Ir
P I 2 r Вт
5

6.

Примеры:
i
Индуктивный элемент
u
I L ( I Lm )
i (t ) I m sin( t i )
di(t )
u L (t ) L
I m L sin( t i 90 )
dt
UL
I m xL sin( t i 90 )
L
U L (U Lm )
U Lm sin( t i 90 )
Фазовый сдвиг
iL uL 90
2
IL
Напряжение на индуктивном элементе опережает ток по фазе на 90°
Закон Ома
Закон Джоуля -Ленца
U IxL
Q I 2 xL ВАр
6

7.

Примеры:
Ёмкостной элемент
i (t ) I m sin( t i )
I С ( I Сm )
С
i
u
С
U С (U Сm )
IC
1
1
uС (t )
I m sin( t i ) I m
sin( t i 90 )
С
C
I m xC sin( t i 90 )
U Cm sin( t i 90 )
Фазовый сдвиг
2
UC
iL uL 90
Напряжение на ёмкостном элементе отстаёт от тока по фазе на 90°
Закон Ома
Закон Джоуля -Ленца
U С IxС
Q I 2 xС ВАр
7

8.

Последовательное соединение rLC в цепи синусоидального переменного тока
i 2 I sin t
u 2U sin( t )
Второй закон Кирхгофа для мгновенных напряжений
u u r u L uC
UL
Составим второй закон Кирхгофа для векторов напряжений
U U r U L UC
Фазовый сдвиг между
током I и напряжением U
Ux
U L UC
arctg
arctg
Ur
Ur
U
UC
Ux= UL- UC
Ur
I
Векторная диаграмма для последовательного
соединения rLC
8

9.

Треугольники напряжений, сопротивлений и мощностей
U
Ux= UL- UC
Ur
полное
Если все стороны треугольника напряжений поделим на I
z
x=xL- xC
реактивное
активное
полная S
активная P
Треугольник напряжений
U 2 U r2 U x2 U r2 (U L U C ) 2
Треугольник сопротивлений
z 2 r 2 x 2 r 2 ( xL xC ) 2
r
Если все стороны треугольника напряжений умножим на I
реактивная
Треугольник мощностей
Q=QL- QC
S 2 P 2 Q 2 P 2 (QL QC ) 2
P S cos UI cos
9

10.

Схемы замещения реальных элементов
1. Реальная катушка индуктивности
Реальная катушка индуктивности замещается последовательно соединенными
идеальными элементами:
• rk активное сопротивление катушки, учитывающие потери;
• xL (L) реактивное сопротивление индуктивности (индуктивность)
zk - полное сопротивление катушки
zк2 rк2 xL2 rк2 ( L) 2
2-й закон Кирхгофа
(в векторной форме)
U к U rк U L
Uк
Определение параметров схемы замещения реальной катушки
Uк
zк
I
rк
P
I2
xL
zк2 rк2
L
xL
Ur
UL
I

11.

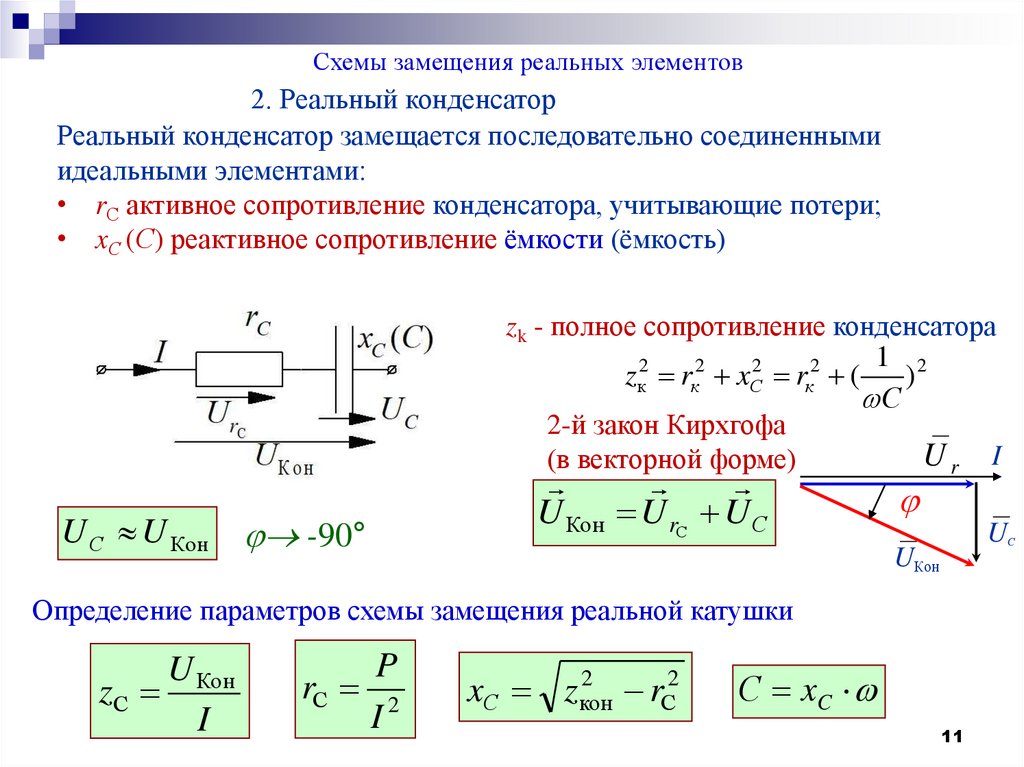
Схемы замещения реальных элементов
2. Реальный конденсатор
Реальный конденсатор замещается последовательно соединенными
идеальными элементами:
• rС активное сопротивление конденсатора, учитывающие потери;
• xС (С) реактивное сопротивление ёмкости (ёмкость)
zk - полное сопротивление конденсатора
1 2
zк2 rк2 xС2 rк2 (
)
С
2-й закон Кирхгофа
Ur I
(в векторной форме)
U С U Кон -90°
U Кон U rС U С
UС
UКон
Определение параметров схемы замещения реальной катушки
U Кон
zС
I
P
rС 2
I
2
xС zкон
rС2
С xC
11

12.

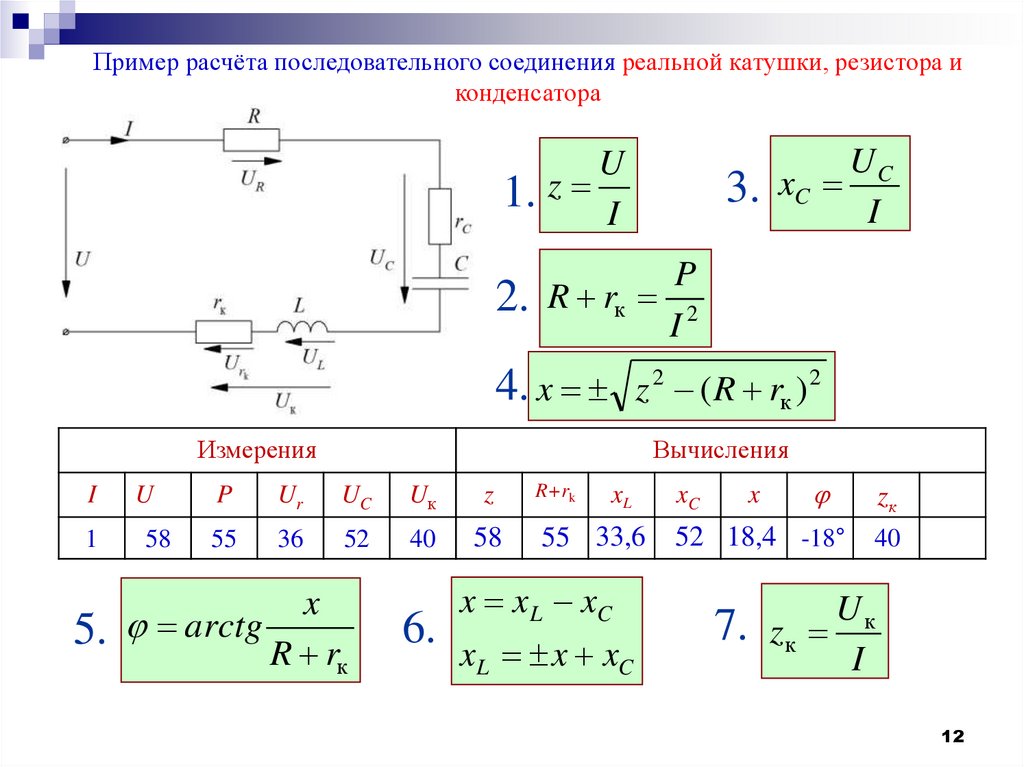
Пример расчёта последовательного соединения реальной катушки, резистора и
конденсатора
UC
3. xC I
U
1. z I
P
2. R rк 2
I
4. x z 2 ( R rк ) 2
Измерения
Вычисления
I
U
P
Ur
UC
Uк
z
R+rk
1
58
55
36
52
40
58
55 33,6
x
5. arctg R r
к
6.
xL
x x L xC
x L x xC
zк
52 18,4 -18°
40
xC
x
Uк
7. zк
I
12

13.

Построение векторной диаграммы
Измерения
Вычисления
I
U
P
UR
UC
Uк
z
R+rk
1
58
55
36
52
40
58
55 33,6
U U R U C U rк U L
Uк U к U rк U L
UL
xL
zк
52 18,4 -18°
40
xC
x
Треугольник сопротивлений
R+rk=55 Ом
z=58 Ом
Urк
UR
I
Треугольник мощностей
U
P=55 Вт
UC
x=xL-xC=18,4 Ом
UС U R
Q=18,5 BAp
S=58 BA
13

14.

14