Похожие презентации:
Расчет электрических цепей переменного тока (лекция 3)
1. БГТУ «ВОЕНМЕХ» им. Д.Ф. Устинова Кафедра электротехники, О8
Лекция 3Расчет электрических цепей
переменного тока
1
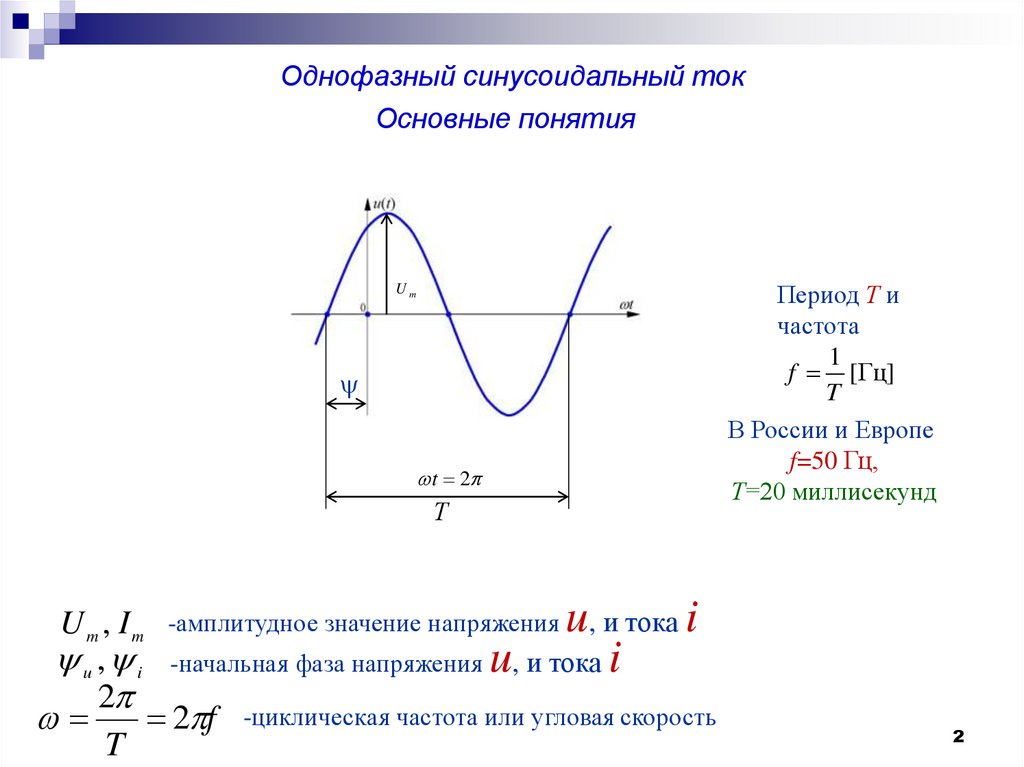
2. Однофазный синусоидальный ток
Основные понятияUm
t 2
Т
U m , I m -амплитудное значение напряжения u, и тока i
u , i -начальная фаза напряжения u, и тока i
2
2 f -циклическая частота или угловая скорость
T
Период Т и
частота
1
f [Гц]
T
В России и Европе
f=50 Гц,
Т=20 миллисекунд
2
3. Мгновенные значения напряжения u(t), тока i(t) и фазовый сдвиг
Мгновенные значения напряжения u(t), тока i(t) и фазовый сдвигi (t ) I m sin( t i )
u (t ) U m sin( t u )
i,u
u
Um
u 0
t
Im
0
i
i 0
Фазовый сдвиг:
i u
3
4.
Однофазный синусоидальный токСредние и действующие значения величин
Среднее значение переменной величины за период Т:
T
1
U ср
udt
T 0
Аналогично вычисляются
Еср и Iср
Среднее значение для мощности за период времени Т:
T
1
P
pdt
T 0
Для оценки периодически изменяющегося напряжения (также ЭДС и
тока) используется и понятие «действующее значение»
Действующим значением переменного периодического сигнала (i(t)) называется
значение такого постоянного сигнала (I), который за один период совершает ту же
работу, что и рассматриваемый переменный.
4
5.
Действующее значение переменной величиныВеличина
Мгновенное значение
Действующее значение
Напряжение
u(t)=Umsin( t+ u)
U
Ток
i(t)=Imsin( t+ i)
I
ЭДС
e(t)=Emsin( t+ e)
E
Работа, совершаемая при приложении напряжения на резистор с сопротивлением r
Постоянное напряжение
Переменное напряжение
T
u2
A
dt
r
0
2
U
A
T
r
Если мгновенное напряжение
u U M sin t
То постоянное напряжение вычислим из равенства работ
1
1 1 cos 2 t
1
U
U M2 sin 2 tdt U M
dt
UM
T0
T0
2
2
T
T
I
1
IM
2
E
1
EM
2
5
6.
Мощность в сети переменного тока1T
1T
P uidt U M sin t I M sin( t )dt
T0
T0
1T
UI (1 cos 2 t ) cos UI sin 2 t sin dt.
T0
UI (1 cos 2 t ) cos 0
Мощность отбирается от сети и совершает полезную работу
P UI cos
UI sin 2 t sin
Активная мощность. Единица измерения - Вт
Q UI sin
Реактивная мощность. Единица измерения - ВАр
Знакопеременная величина. Средняя значения за период =0!
Наибольшее значение активной мощности, возможное при данных значениях
напряжения и тока, называется полной мощностью и обозначается S:
S=UI
[ВА]
S P2 Q2
6
7.
Соотношение действующих значений напряжения и тока и сдвиг по фазе в цеписинусоидального переменного тока
Мгновенные значения тока i(t) и
напряжения u(t) на зажимах двухполюсника:
i 2 I sin t
u 2U sin( t )
Составим уравнение на основании второго закона Кирхгофа для замкнутого контура:
di 1
idt
dt C
Закон Ома:
Для резистора:
u r 2 Ir sin t
U r Ir
Для индуктивности:
u L 2 I L cos t 2 Ix L cos t
u ur u L uC ir L
u L 2 Ix L sin( t
Для емкости:
uC 2 I
2
)
U L Ix L
1
cos t 2 IxC cos t
C
uC 2 Ix C sin( t
2
)
U C IxC
7
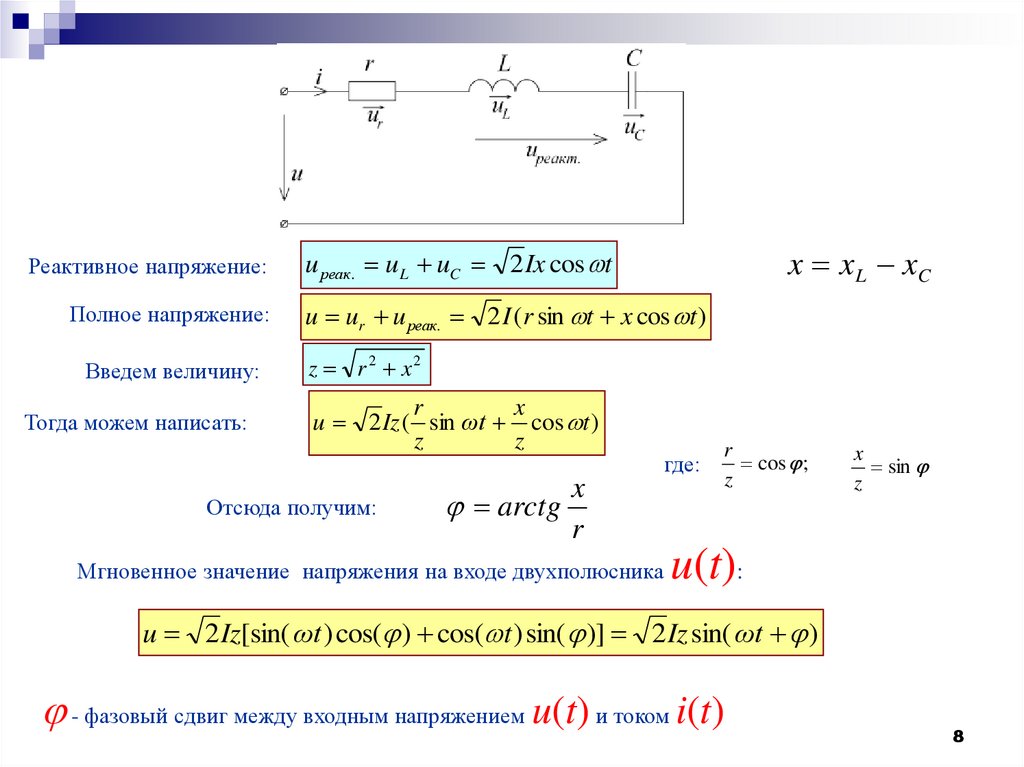
8.
Реактивное напряжение:Полное напряжение:
Введем величину:
Тогда можем написать:
x x L xC
u реак. uL uC 2 Ix cos t
u ur u реак. 2 I ( r sin t x cos t )
z r 2 x2
r
x
u 2 Iz ( sin ωt cos t )
z
z
Отсюда получим:
arctg
x
r
Мгновенное значение напряжения на входе двухполюсника
где:
r
cos ;
z
x
sin
z
u(t):
u 2 Iz[sin( ωt ) cos( ) cos( t ) sin( )] 2 Iz sin( ωt )
- фазовый сдвиг между входным напряжением u(t) и током i(t)
8
9.
введённые выше величины:xL , xC , x, z - имеют размерность сопротивления (Ом).
Поэтому в соответствии с их физическим смыслом – они называются:
x
xL
xC
- реактивное сопротивление;
- индуктивное сопротивление;
- ёмкостное сопротивление;
U r Ir
U L Ix L
z – полное сопротивление
U C IxC
Подставляя данные величины в формулы мощности:
U Iz
P I r;
2
Q I 2 x;
Закон Ома:
S I 2z
Реактивную мощность можем представить в виде:
Q I 2 ( x L xC ) I 2 x L I 2 xC QL QC
9
10.
Параллельное соединение элементов:Приложенное напряжение:
u 2U sin t
Входящий ток можем найти в виде:
i 2 I sin( t )
bL
индуктивная проводимость;
ёмкостная проводимость;
реактивная проводимость;
b
полная проводимость;
y
Единица измерения – (Сим) Сименс
bС
Закон Ома:
Для данной схемы:
1
bL
;
L
bC C ;
b bL bC ;
y
g 2 b2
I r Ug
-для активной проводимости (g);
I L UbL
-для индуктивной проводимости (bL);
I C UbC
-для ёмкостной проводимости (bС);
I реак. Ub -для реактивной проводимости(b);
I Uy
-для полной проводимости (y);
10








 Физика
Физика Электроника
Электроника








