Координаты и векторы

1. Координаты и векторы

2. Студент должен знать:

• Прямоугольная (декартова) система координат в
пространстве.
• Формула расстояния между двумя точками.
• Понятие вектора. Модуль вектора. Равенство
векторов.
• Сложение векторов.
• Умножение вектора на число. Разложение вектора по
направлениям. Угол между двумя векторами.
• Проекция вектора на ось. Координаты вектора.
Скалярное произведение векторов.
• Использование координат и векторов при решении
математических и прикладных задач.

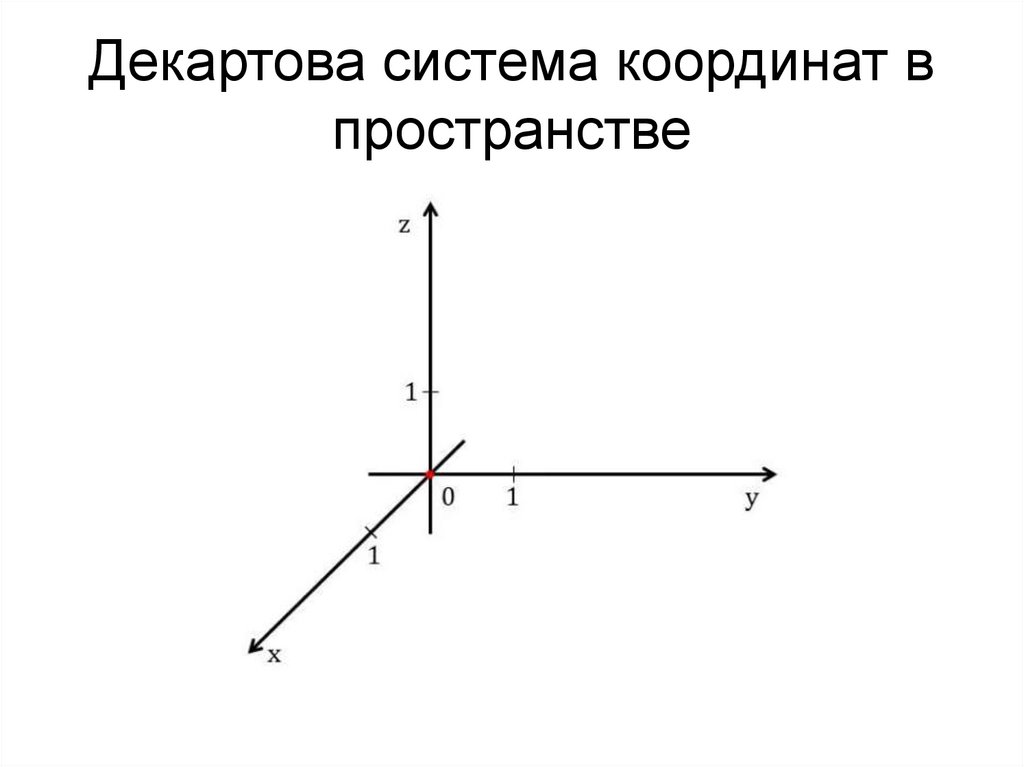
3. Декартова система координат в пространстве

Прямоугольная система координат в
пространстве образуется тремя
взаимно перпендикулярными осями
координат OX, OY и OZ.
Ох - ось абсцисс,
Оу - ось ординат
Оz - ось аппликат

4. Декартова система координат в пространстве

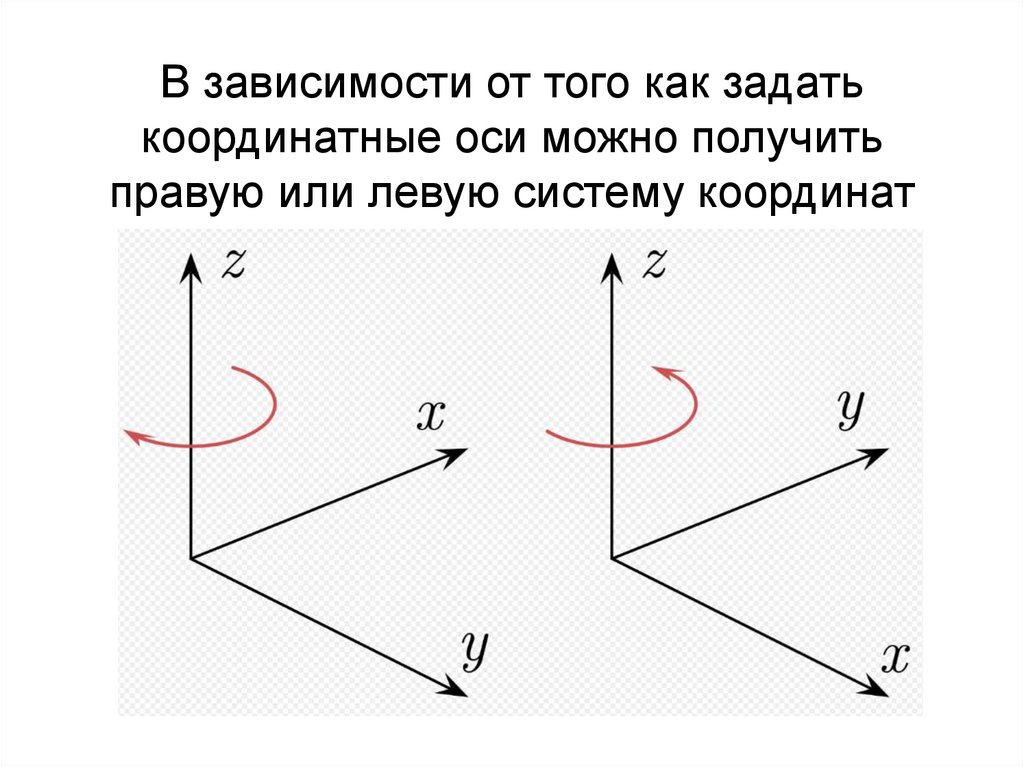
5. В зависимости от того как задать координатные оси можно получить правую или левую систему координат

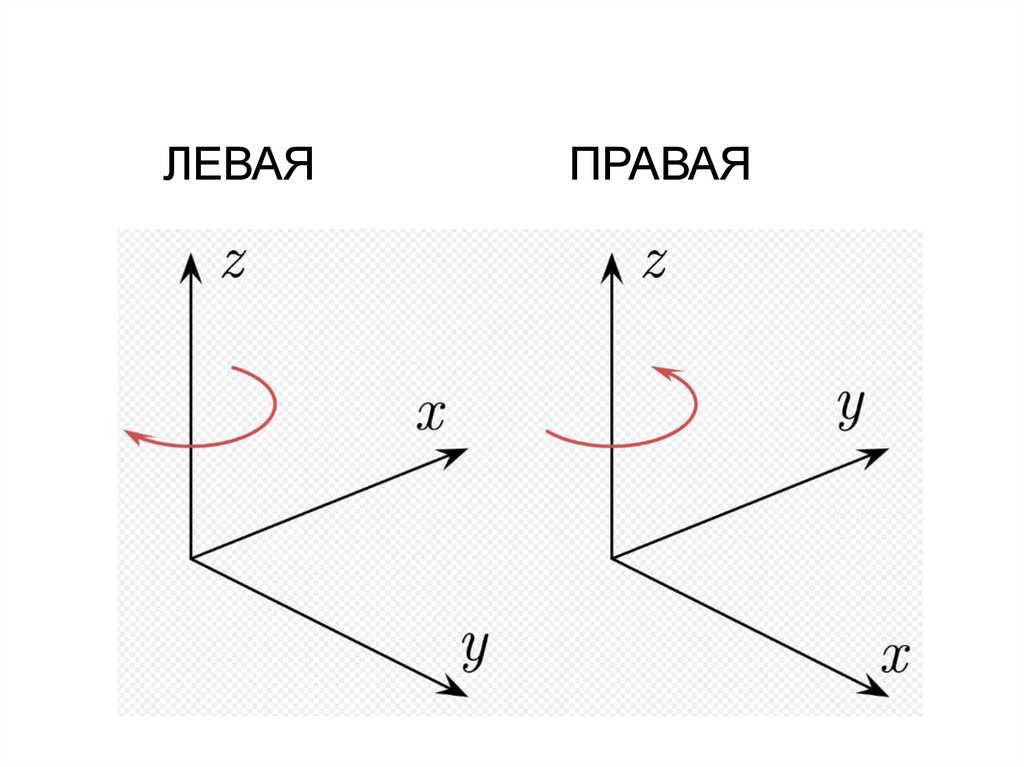
6. Общепринятая – правая система координат

Положительное направление осей
выбирают так, чтобы при повороте оси
OX против часовой стрелки на 90° её
положительное направление совпало с
положительным направлением оси OY,
если этот поворот наблюдать со
стороны положительного направления
оси OZ.

7. ЛЕВАЯ ПРАВАЯ

8. Декартова система координат в пространстве

Точка М задается тремя координатами (х,у,z)

9. Формула вычисления расстояния между двумя точками:

Даны две координаты в пространстве:
точка А( ха , yа , zа ) и В( хb , yb , zb )
Длина отрезка АВ находится по формуле:
АВ ( хb хa )2 ( уb уa )2 ( zb za )2

10. Задания

1. Найти расстояние между точками:
а) А (1,2,3)
и А ( 1,1,1)
1
б)
В1 (3,4,0)
2
и
В2 (3, 1,2)

11. Координаты середины отрезка

Пусть дана точка А( х1, y1, z1 ) и
точка B( х2 , y2 , z2 ) . Точка С – середина
отрезка АВ, тогда
у1 у2
х1 х2
;
х
; у
2
2
z1 z2
z
2

12. Задания

2. Найти координаты середины отрезка
а) GH, если
G (2, 3,5)
H (4,1, 3)
б) АВ, если
A(3, 2,4)
B (5,2, 6)

13. Домашнее задание

Даны точки М (1, 2, 3)
N ( 2,3,1)
K (3,1, 2)
Найти периметр треугольника MNK

14. Понятие вектора

Какие понятия характеризуют вектор?
• Форма
• Объем
• Направление
• Величина
Какие физические величины можно
задать с помощью вектора?
Что такое вектор?

15. Определение

Вектор – направленный отрезок,
который имеет начало и конец.
Обозначение:
или
а
где: А – начало вектора
В – конец вектора
АВ

16.

Любая точка пространства
рассматривается как нулевой вектор.
Обозначается:
0
Длина вектора (модуль вектора)
обозначается:
|a|
или
| АВ |

17. Коллинеарные векторы

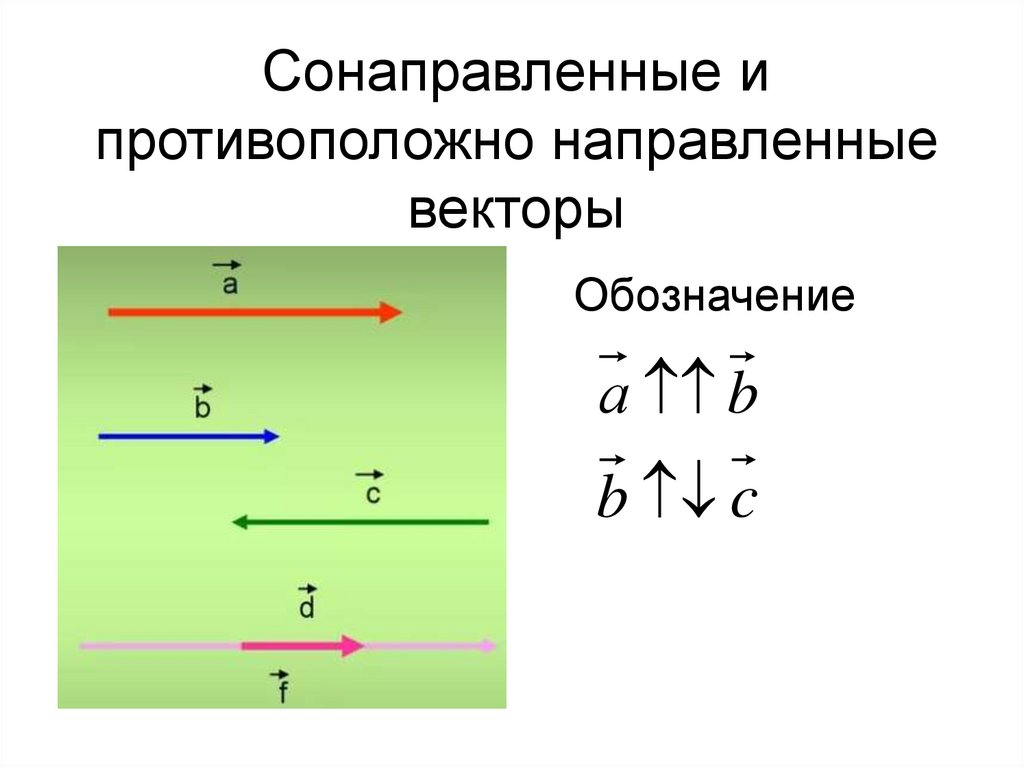
18. Сонаправленные и противоположно направленные векторы

Обозначение
а b
b c

19.

Нулевой вектор
считается
сонаправленным
с любым вектором.
0

20. Определение

Векторы называются равными, если
они сонаправлены и их длины равны.
От любой точки можно отложить вектор,
равный данному, и притом только один.

21. Действия над векторами

22. Действия над векторами

1. Сложение
2. Вычитание
3. Умножение на число

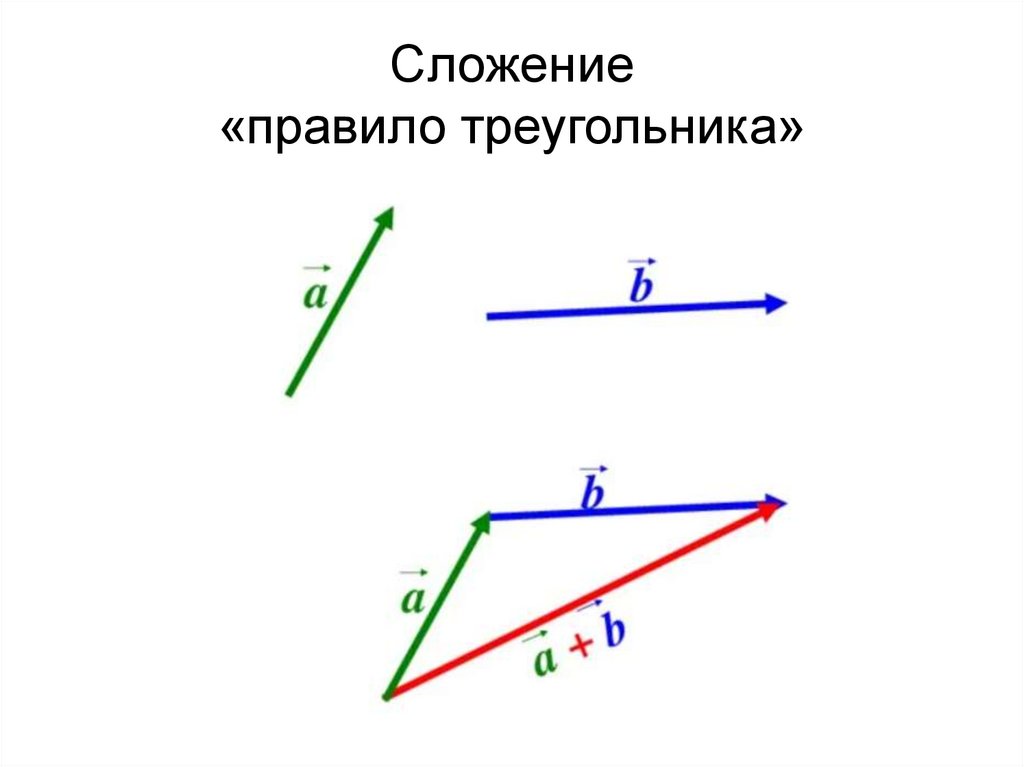
23. Сложение «правило треугольника»

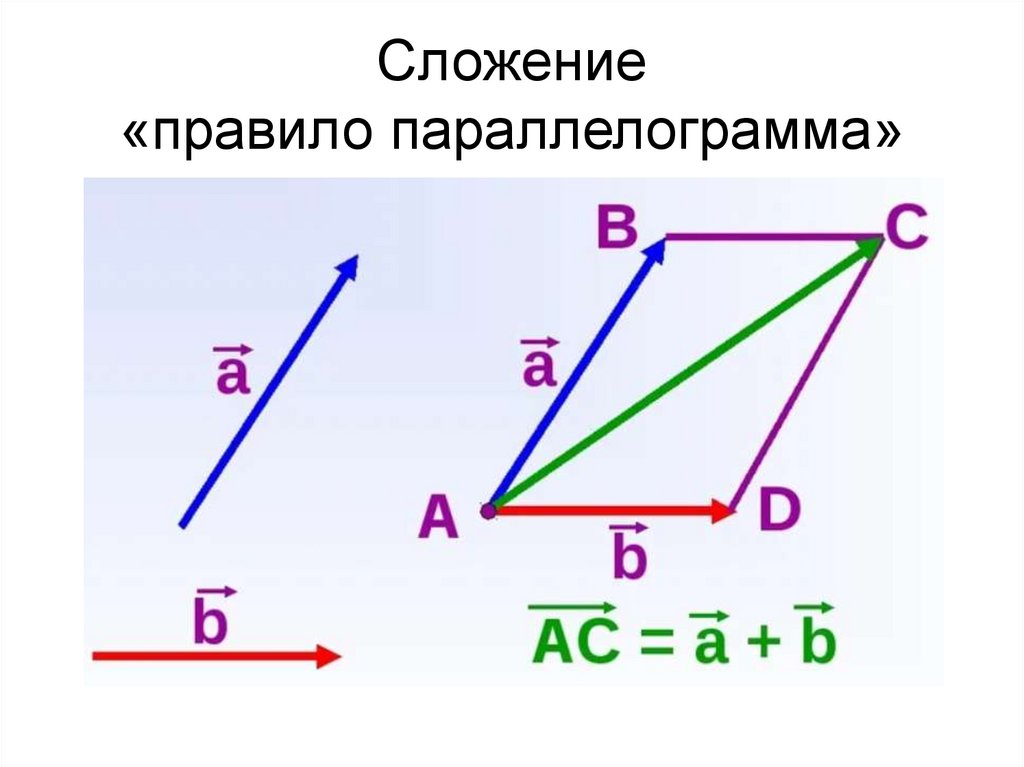
24. Сложение «правило параллелограмма»

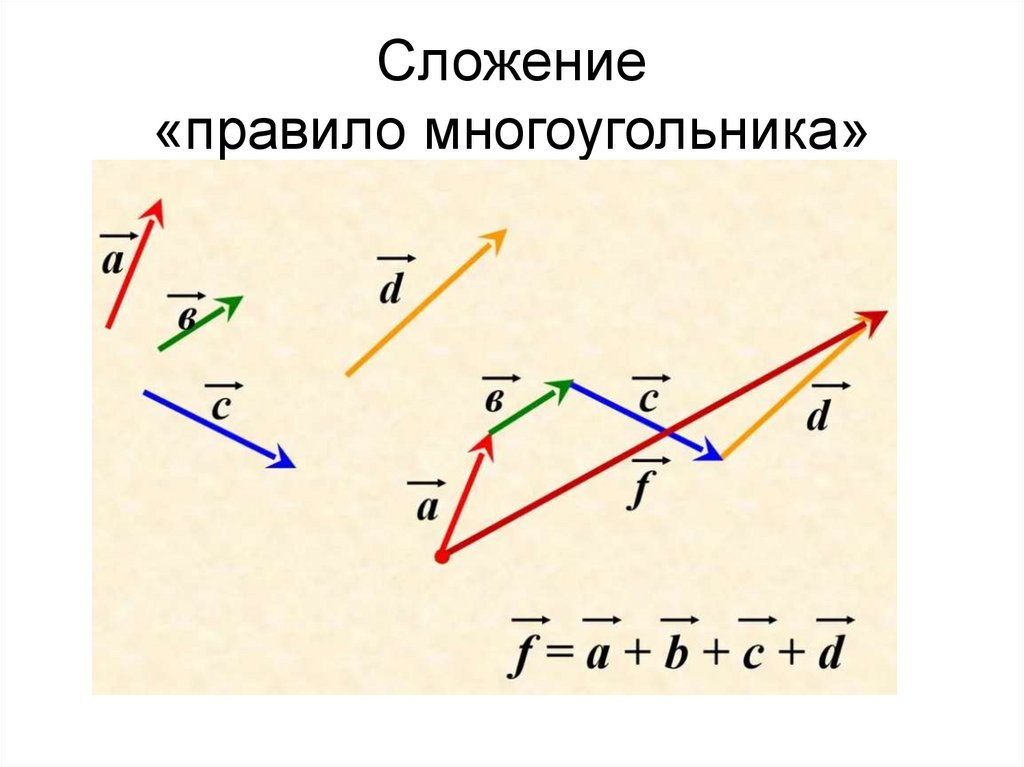
25. Сложение «правило многоугольника»

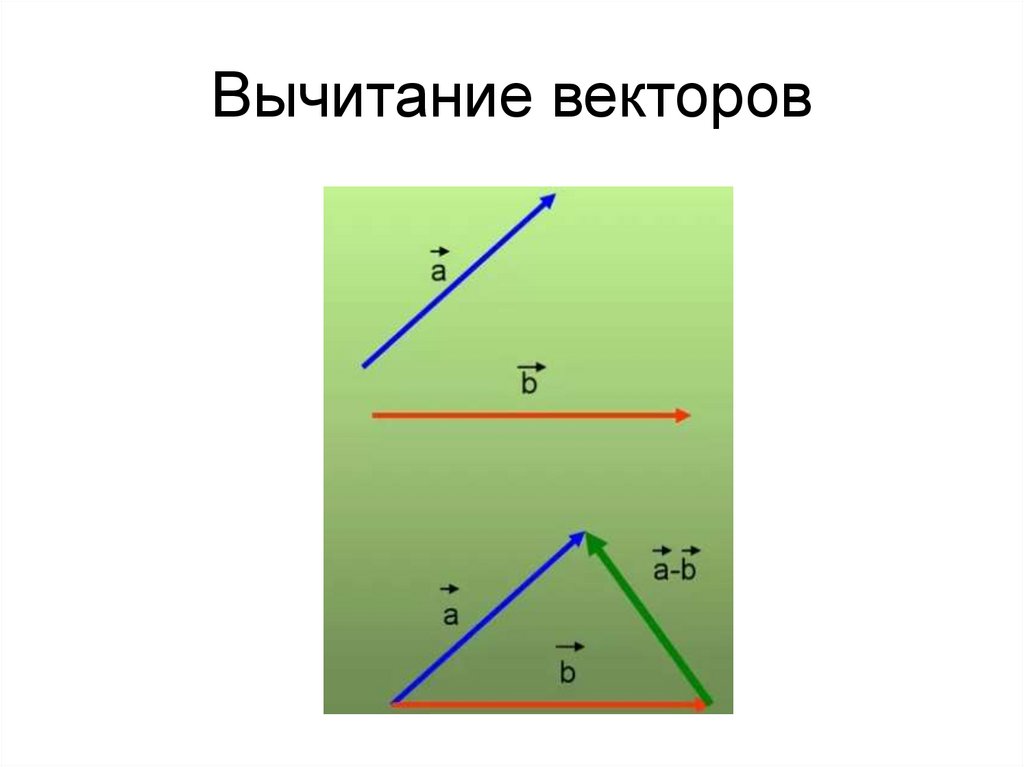
26. Вычитание векторов

27. Вопросы

• Что такое вектор?
• Как изображается в пространстве
нулевой вектор?
• Что такое коллинеарные векторы?

28. Умножение вектора на число

Определение.
Вектор k a (ka1, ka2 , ka3 ) называется
умножением вектора a (a , a , a )
1 2
3
на число k.

29. Векторы

a
и
k a
К>0 сонаправлены
a k a
K<0 противоположно направлены
a k a

30. Умножение вектора на число

Произведением нулевого вектора на
произвольное число считается нулевой
вектор.
0 k 0
0 a 0

31. Свойства операции умножения вектора на число

Для любых векторов a ,
k и m
a) k (а b) k a k b ;
b) (k m)a k a ma ;
c) | k a | | k | | a |
b
и чисел

32. Длина вектора

А( ха , уа , zа )
В( хb , уb , zb )
| АВ | ( хb хa ) ( уb уa ) ( zb za )
2
2
2

33. Длина вектора

Если вектор задан координатами
a х, y, z
| а | x y z
2
2
2

34. Задание 1

Даны координаты четырех вершин
куба ABCDA1B1C1D1:
А (0; 0; 0), В (0; 0; 1),
D (0; 1; 0), А1 (1; 0; 0).
Найдите координаты остальных
вершин куба.

35. Задание 2

Задан параллелепипед
ABCDA1B1C1D1. Запишите вектор,
начало и конец которого являются
вершинами параллелепипеда, равный
сумме векторов:
а) AB + A1D1; г) DD1+DB;
б) AB + AD1; д) DB1+ ВС.
в) DA + B1B;

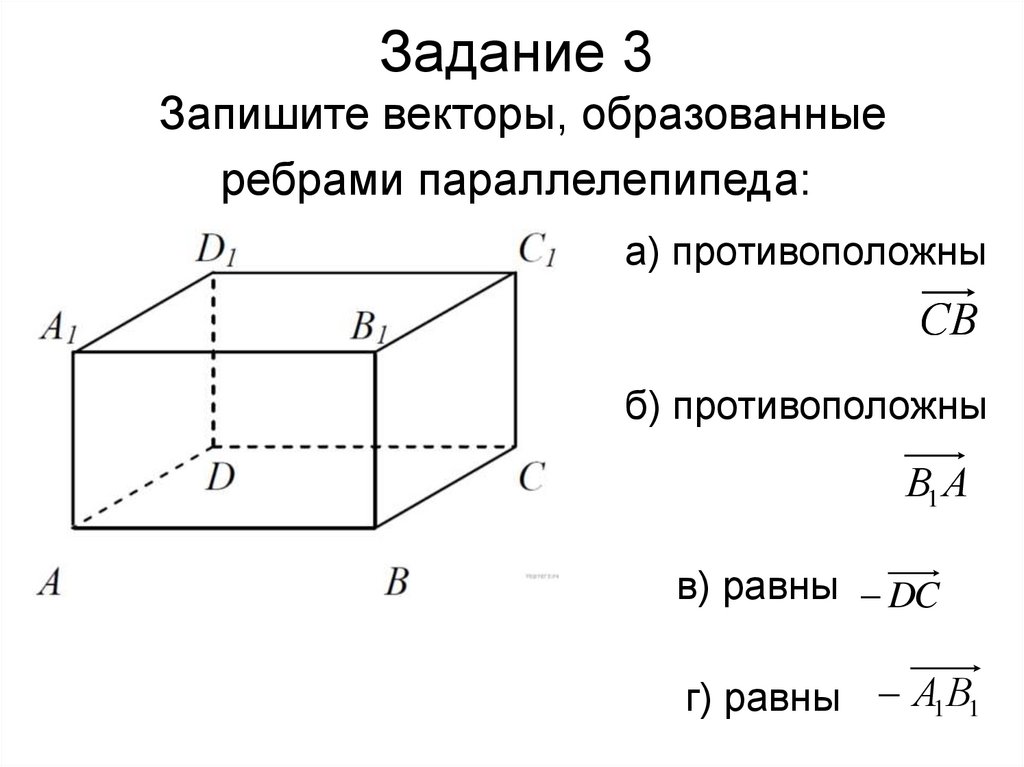
36. Задание 3 Запишите векторы, образованные ребрами параллелепипеда:

а) противоположны
СВ
б) противоположны
В1 А
в) равны DC
г) равны А1В1

37. Разложение вектора по базису

38. Скалярное произведение векторов

а b | a | | b | cos
φ - угол между векторами
а
и
b

39. Скалярное произведение векторов

Если векторы заданы координатами,
а хa , уa , za
b хb , уb , zb
то формула скалярного произведения
имеет вид
а b хa хb уa уb za z b

40. Условие перпендикулярности векторов

а b 0
(Скалярное произведение векторов равно нулю)

41. Условие коллинеарности векторов

Даны векторы
а хa , уa , za
b хb , уb , zb
если они коллинеарны, то:
хa уa za
хb уb zb

42. Формула центра тяжести треугольника, вершины которого заданы координатами

х1 х2 х3 у1 у2 у3 z1 z 2 z3
( хс , ус , zс )
,
,
3
3
3

43. Формулы

Длина вектора:
| а | x y z
Угол между векторами:
2
2
2
a b
cos
| a | |b |
Координаты середины сторон:
у1 у2
х1 х2
;
х
; у
2
2
z1 z2
z
2