Теоремы об углах, образованных двумя параллельными

1.

2.

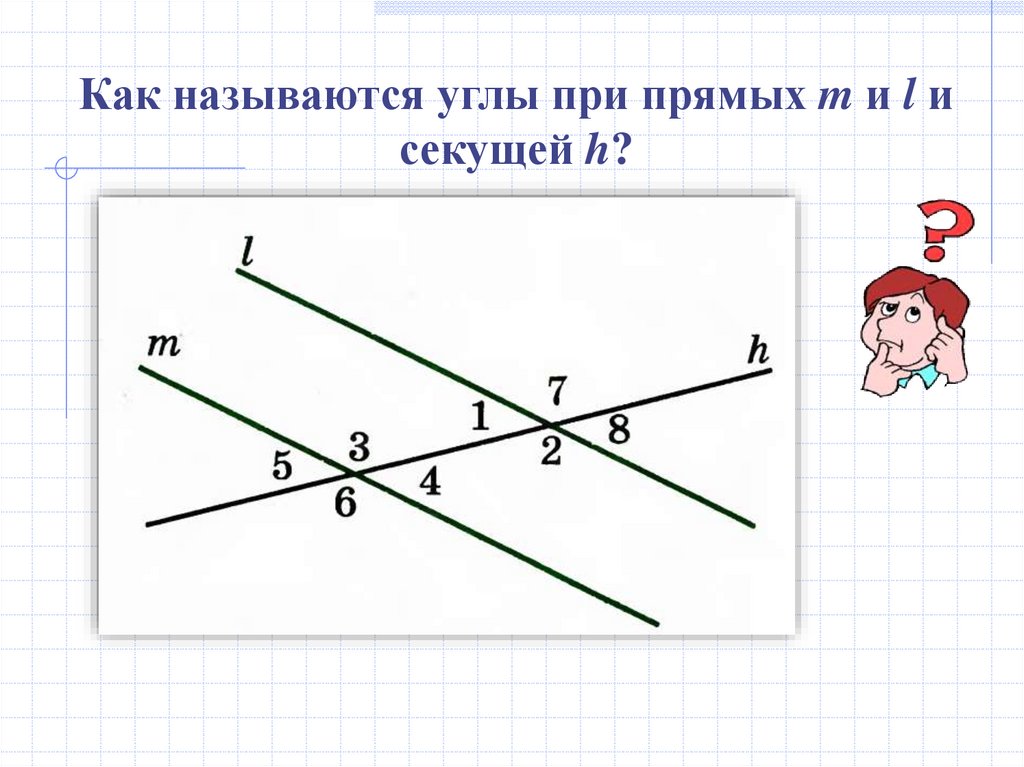
Как называются углы при прямых m и l и
секущей h?

3.

Признаки параллельности прямых
c
Если при пересечении двух прямых
секущей накрест лежащие углы равны,
то прямые параллельны.
Если при пересечении двух прямых
секущей соответственные углы равны,
то прямые параллельны.
Если при пересечении двух прямых секущей
сумма односторонних углов равна 1800, то
прямые параллельны.
а
1
2
b
c
1
а
2
b
c
а
1
2
b

4.

5.

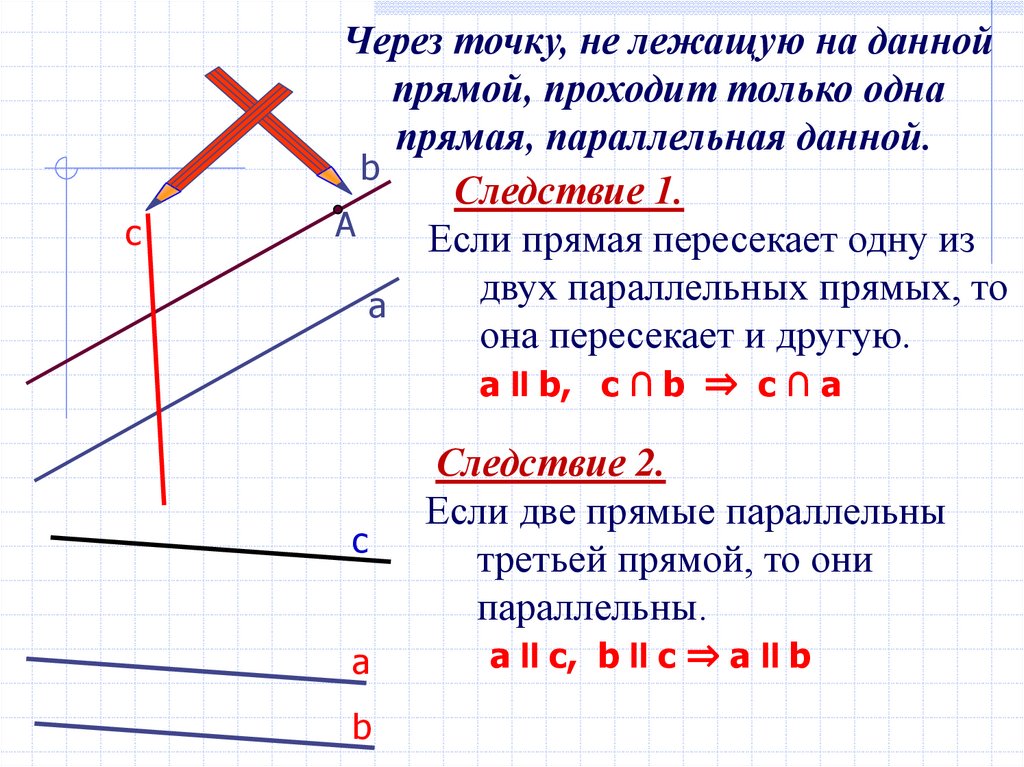
c
Через точку, не лежащую на данной
прямой, проходит только одна
прямая, параллельная данной.
b
Следствие 1.
А
Если прямая пересекает одну из
двух параллельных прямых, то
а
она пересекает и другую.
a II b, c ∩ b ⇒ c ∩ a
с
а
b
Следствие 2.
Если две прямые параллельны
третьей прямой, то они
параллельны.
a II с, b II с ⇒ a II b

6.

7.

Если две параллельные прямые пересечены
секущей, то накрест лежащие углы равны.
Р
1
N
2
M
а
b
Дано: a II b, MN- секущая.
Доказать: 1= 2 (НЛУ)
Доказательство:
способ от противного.
Допустим, что 1 2.
Отложим от луча МN угол NМР, равный углу 2.
По построению накрест лежащие углы ∠NМР= ∠ 2 =>
РМ II b.
Получили, что через точку М проходит две прямые (а и МР),
параллельные прямой b !!! Это противоречит аксиоме
параллельных прямых. Значит наше допущение неверно!!!
1= 2.
Теорема доказана.

8.

Если две параллельные прямые пересечены
секущей, то сумма односторонних углов равна 1800.
c
а
3
1
2
b
Дано: а II b, c- секущая.
Доказать: OУ 1+ 2=1800.
Доказательство:
3+ 2 =1800, т. к. они смежные.
11= 3, т. к. это НЛУ при а II b
3 + 2 =1800
Теорема доказана.

9.

Если две параллельные прямые пересечены
секущей, соответственные углы равны.
c
2
а
3
1
b
Дано: а II b, c- секущая.
Доказать: СУ 1 = 2.
Доказательство:
2 = 3, т. к. они вертикальные.
3 = 1, т. к. это НЛУ при а II b
22
11 = 3 =
Теорема доказана.

10.

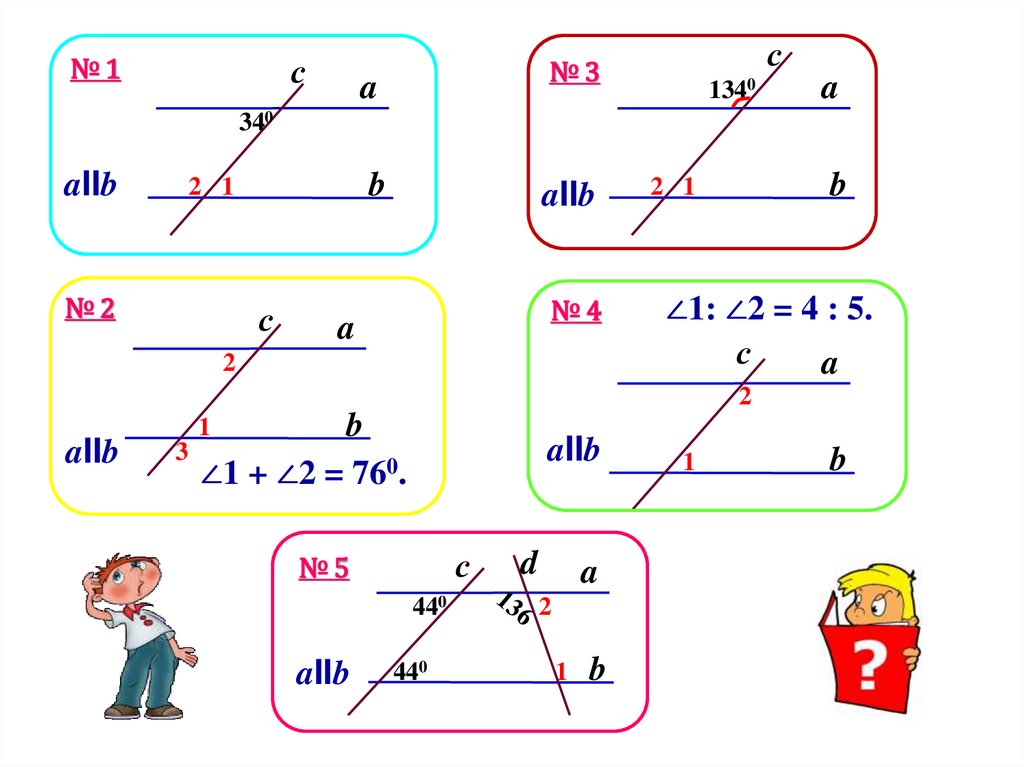
с
№1
с
№3
a
1340
a
340
aIIb
b
2 1
№2
с
a
b
aIIb
2 1
№4
∠1: ∠2 = 4 : 5.
с
a
2
2
aIIb
b
3
∠1 + ∠2 = 760.
1
aIIb
с
№5
440
aIIb
440
d
a
2
1
b
1
b

11.

стр. 58 – 63, учить аксиомы,
теоремы и их доказательства

12.

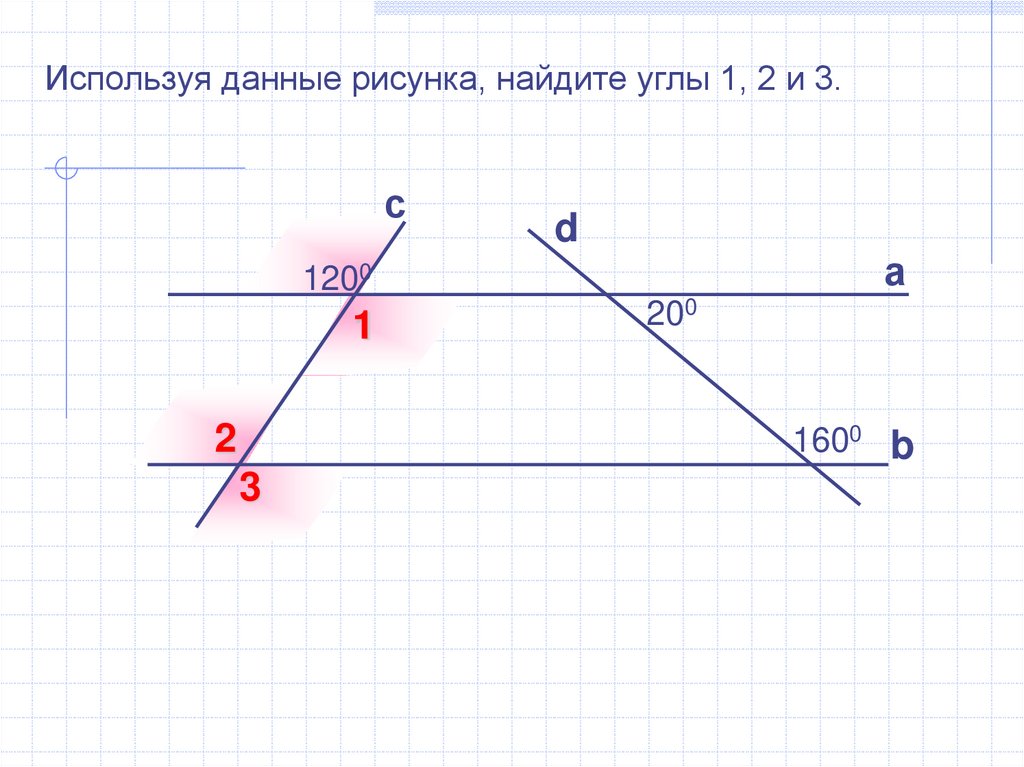
Используя данные рисунка, найдите углы 1, 2 и 3.
с
d
а
1200
1
2
200
1600 b
3

13.

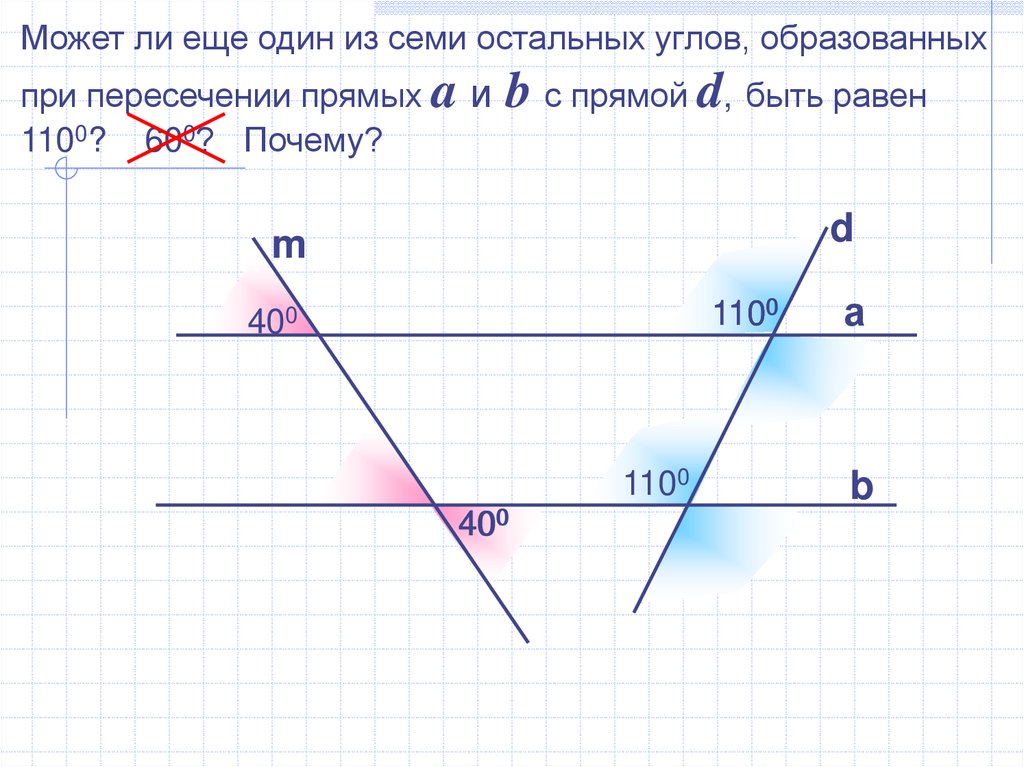
Может ли еще один из семи остальных углов, образованных
при пересечении прямых a и b с прямой d, быть равен
1100? 600? Почему?
d
m
1100
400
1100
400
а
b

14.

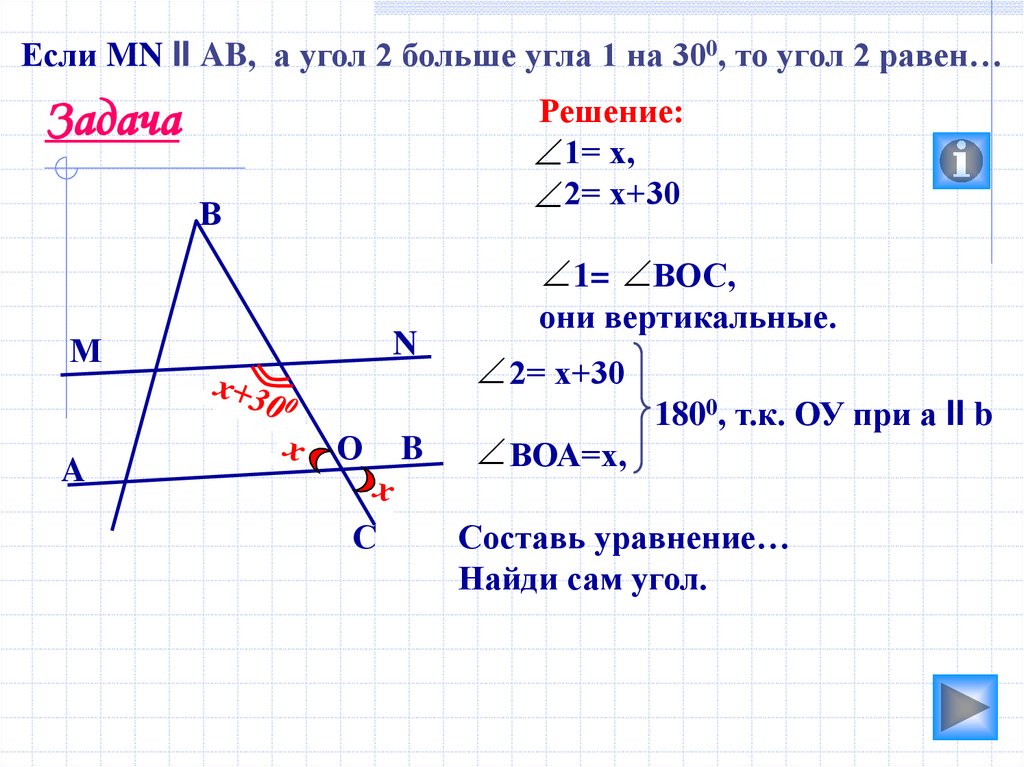
Если MN II AB, а угол 2 больше угла 1 на 300, то угол 2 равен…
Решение:
1= х,
2= х+30
Задача
В
1= ВОС,
N
М
2
A
О
1
С
B
они вертикальные.
2= х+30
ВОА=х,
1800, т.к. ОУ при а II b
Составь уравнение…
Найди сам угол.

15.

Тренировочные упражнения
Дано: а II b, с – секущая
1 = 4 2
Найдите:
1 и 2
c
а
Угол 1 в 4 раза больше
угла 2
1
4х
2х
b

16.

Тренировочные упражнения
Угол 1 на 300 больше
угла 2
Дано: а II b, с – секущая
1 – 2 = 300
Найдите:
1 и 2
c
а
1
х+30
2х
b

17.

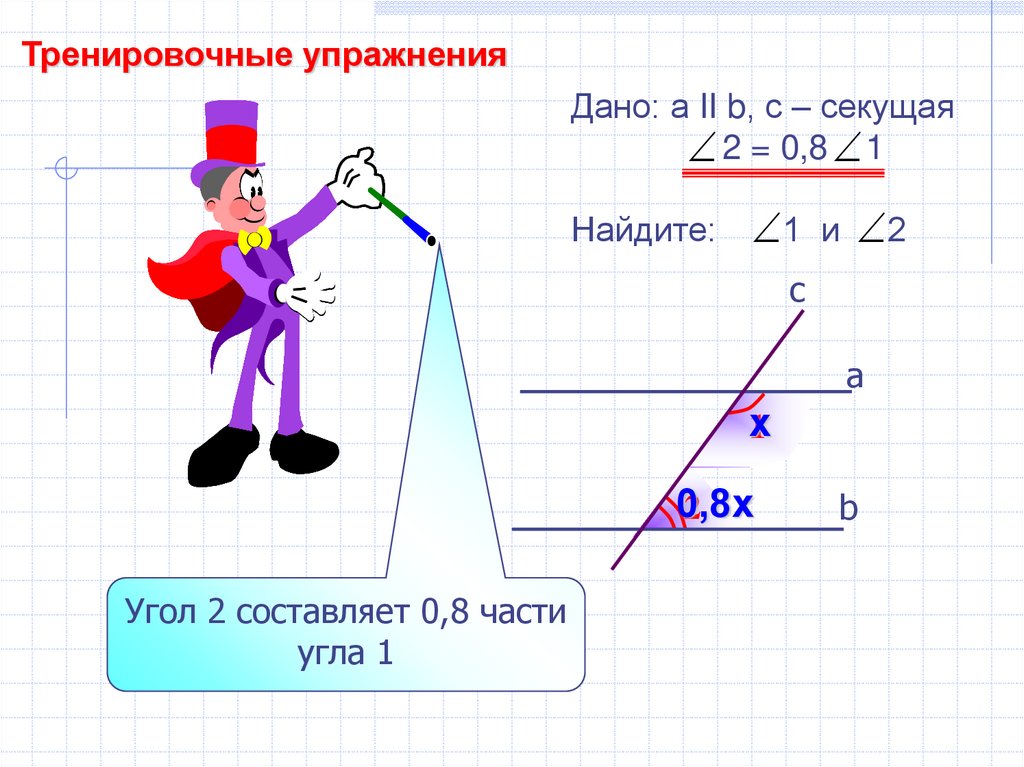
Тренировочные упражнения
Дано: а II b, с – секущая
2 = 0,8 1
Найдите:
1 и 2
c
а
1х
0,8х
2
Угол 2 составляет 0,8 части
угла 1
b

18.

Тренировочные упражнения
Пусть х – 1 часть
Дано: а II b, с – секущая
1 : 2 = 5 : 4
Найдите:
1 и 2
c
а
5х
1
5:4
4х
2
b

19.

Тренировочные упражнения
Дано: а II b, с – секущая
2 составляет 80% от 1
Найдите:
1 и 2
c
%
а
х
1
0,8х
2
b

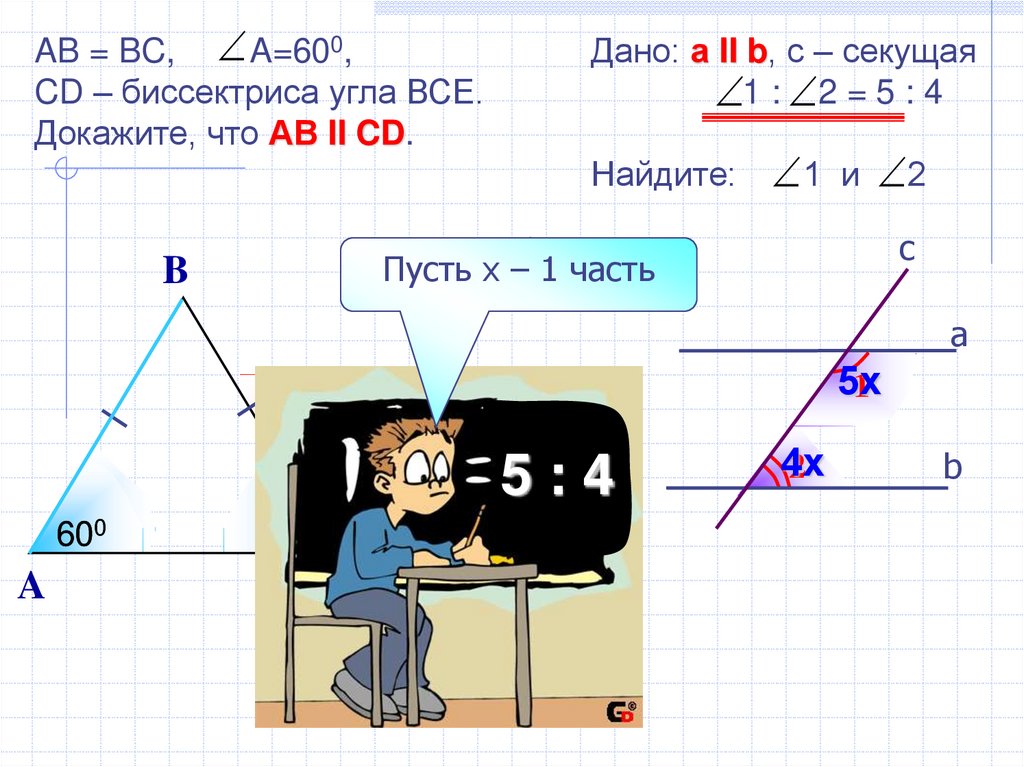
20.

AB = BC, A=600,
CD – биссектриса угла ВСЕ.
Докажите, что АВ II CD.
Дано: а II b, с – секущая
1 : 2 = 5 : 4
Найдите:
1 и 2
c
Пусть х – 1 часть
B
D
а
5х
1
1200
5:4
С
E
600
600
A
600
4х
2
b

21.

На рисунке АС II ВD и
Найдите СВD.
A
АС = АВ,
МАС = 400.
M
С
400
2
3
B
1
D

22.

На рисунке АВ II ЕD.
Докажите, что ВСD = B + D
B
Подсказка
A
1
N
2
3
C
Построим CN II AB
4
D
E

23.

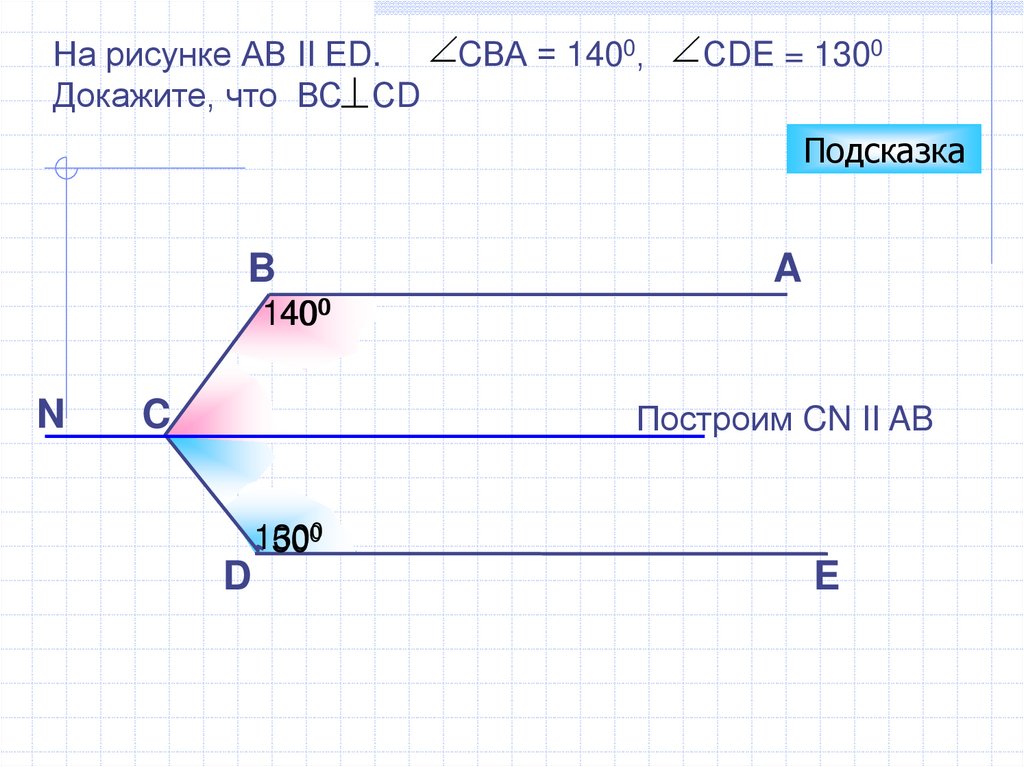
На рисунке АВ II ЕD. CВА = 1400, СDE = 1300
Докажите, что ВС СD
Подсказка
B
A
140
400
N
C
Построим CN II AB
130
50 0
D
E

24.

a II b, c – секущая, DM и DN – биссектрисы
смежных углов, образованных прямыми a и c. DE = 5,8 см
На рисунке
Найдите MN.
с
а
400 D
2
3 6
5
1
M
4
E
?
b
N

25.

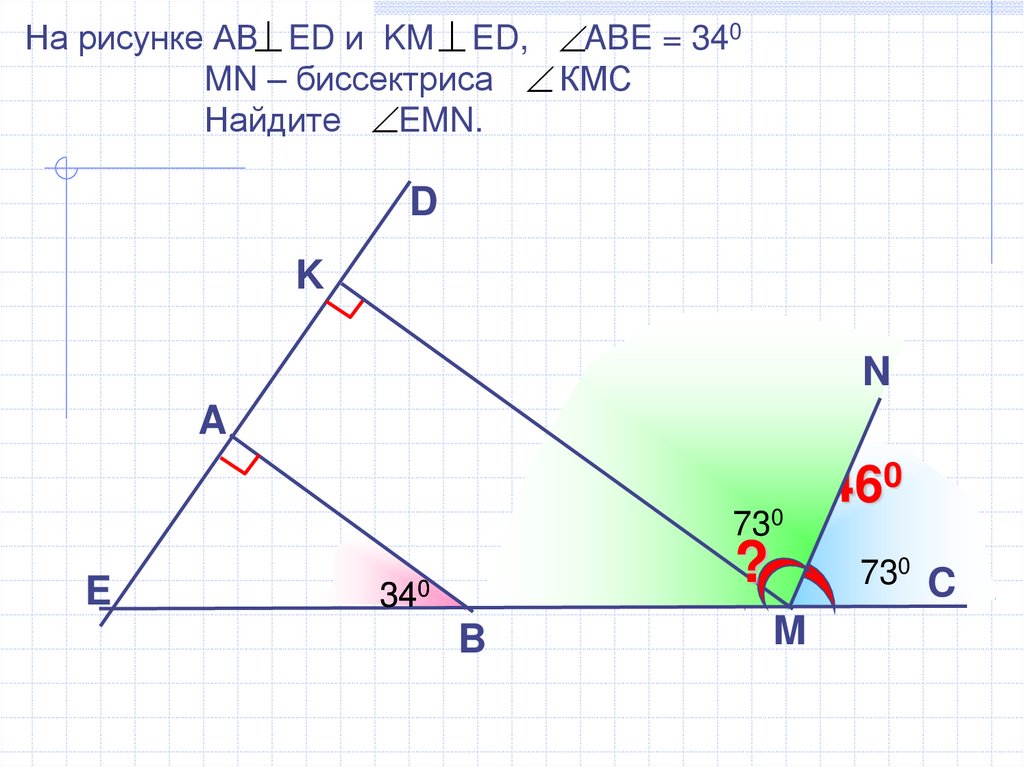
На рисунке АВ ED и KM ED, ABE = 340
MN – биссектриса КМС
Найдите EMN.
D
K
N
A
0
146
0
73
E
?
340
B
730 C
M

26.

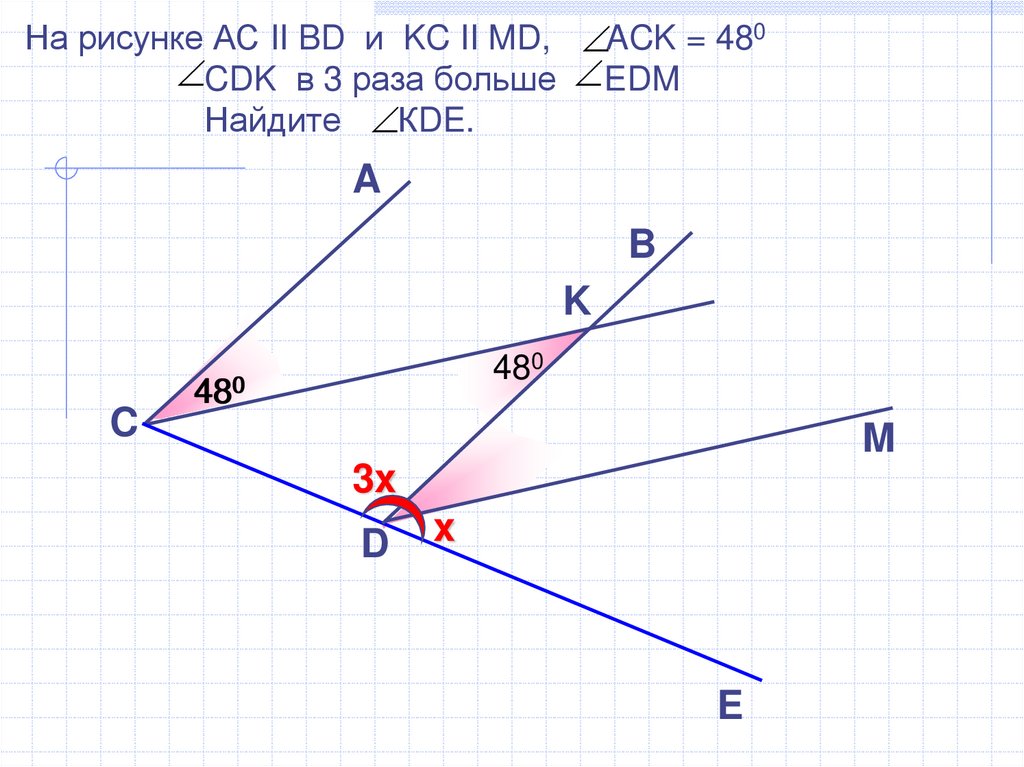
На рисунке АС II BD и KC II MD, ACK = 480
CDK в 3 раза больше EDM
Найдите КDE.
A
B
K
C
480
480
M
3x
D
x
E