Похожие презентации:
Теорема об углах, образованных двумя параллельными прямыми и секущей
1.
«Учиться - это открывать двери в мир возможностей.»Фрэнк Шерман
06.02.2024
2.
Теоремой обратной данной называется такая теорема, гдеусловием является заключение исходной теоремы, а заключением
ее условие
Пример
Условие Если при пересечении двух прямых секущей накрест лежащие
Заключение
углы равны,
То прямые параллельны.
Обратная теорема
Условие
Если прямые параллельны при пересечении двух прямых
секущей,
Заключение То накрест лежащие углы равны,
3.
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫСЕКУЩЕЙ,
ТО НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ.
4.
PЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ
СЕКУЩЕЙ, ТО НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ.
M
а
1
2
в
N
1)
2)
3)
d
Дано: прямые a ∥ b, секущая MN;
1 и 2 – накрест лежащие;
Доказать: 1 = 2;
Доказательство.
Предположим, что 1 ≠ 2;
Отложим от луча MN ∠PMN = 2, так чтобы ∠PMN и 2 были накрест лежащими углами при
пересечении прямых MP и b секущей MN;
По построению эти накрест лежащие углы равны, поэтому MP ∥ b. (по признаку
параллельности двух прямых)
4)
5)
Мы получили, что через точку М проходят 2 прямые параллельные прямой b. Что противоречит
аксиоме параллельных прямых.
Значит, наше допущение неверно и 1 = 2;
Q.E.D
5.
са
b
M
1
2
N
Если прямая перпендикулярна к одной из двух
параллельных прямых,
то она перпендикулярна и к другой.
Дано: прямые a ∥ b, c a
Доказать: c b
Доказательство.
Прямая c пересекает прямую a , при этом a ∥ b , значит b пересекает и прямую (следствие 20 из
аксиомы параллельных прямых). При пересечении
параллельных прямых a и b секущей c образуются равные накрест лежащие углы:
1 = 2 (по теореме о накрест лежащих углах). По условию c a, т.е. 1 = 900, значит и 2 = 900 ,
т.е. c b
Q.E.D
6.
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫСЕКУЩЕЙ,
ТО СООТВЕТСТВЕННЫЕ УГЛЫ РАВНЫ.
7.
сM
3
а
b
1
N
2
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ, ТО СООТВЕТСТВЕННЫЕ
УГЛЫ РАВНЫ.
Дано: прямые a ∥ b, секущая MN;
1 и 2 – соответственные;
Доказать: 1 = 2;
Доказательство.
По условию a ∥ b , следовательно накрест лежащие углы 1 и 3 равны, т.е. 1 = 3 (по теореме о
накрест лежащих углах). При этом 2 = 3 как вертикальные углы.
Из равенств 1 = 3 и 2 = 3 следует, что 1 = 2.
Q.E.D
8.
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫСЕКУЩЕЙ, ТО СУММА ОДНОСТОРОННИХ УГЛОВ РАВНА
180⁰.
9.
сM
а
в
3
2
N
1
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ
СЕКУЩЕЙ, ТО СУММА ОДНОСТОРОННИХ УГЛОВ
РАВНА 180⁰.
Дано: прямые a ∥ b, секущая MN;
1 и 2 –односторонние;
Доказать: 1 + 2 = 180⁰;
Доказательство.
По условию a ∥ b, значит соответственные углы 2 и 3 равны, т.е. 2 + 3 (по теореме о
соответственных углах). При этом 1 и 3 - смежные, следовательно, их сумма равна 1800, т.е.
1 + 3 = 1800.
Из равенств 2 + 3 и 1 + 3 = 1800 следует, что 1 + 2 = 1800
Q.E.D
10.
са
в
4 3
5 1
6
2
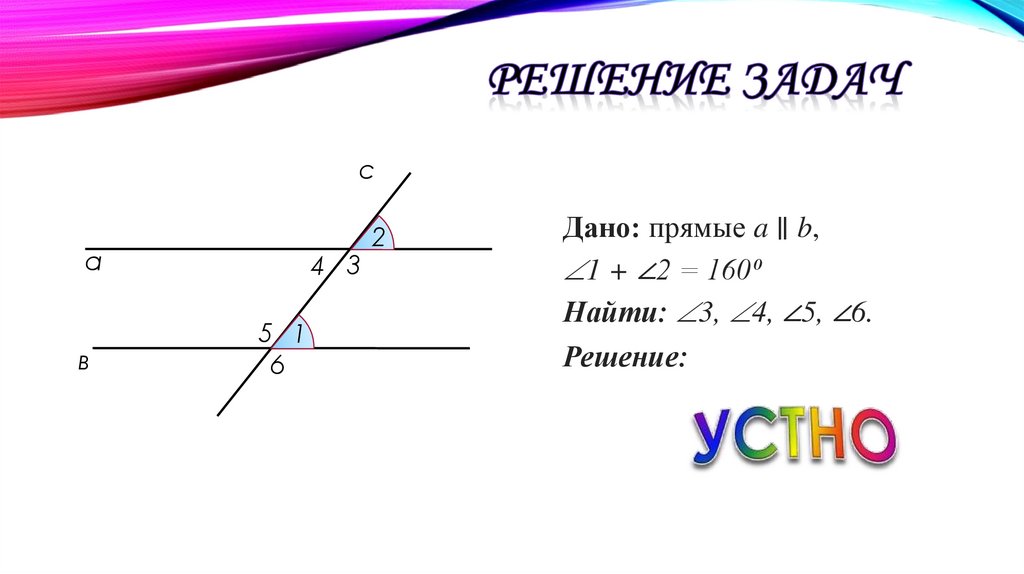
Дано: прямые a ∥ b,
1 + ∠2 = 160⁰
Найти: 3, 4, ∠5, ∠6.
Решение:
11.
Откройте учебник на странице 66, Выполняем номера 210, 21312.
§ 29, § 30 Выучить Теоремы и их следствия№ 211, № 212
13.
Чем лично для вас был интересен этот урок?Какие формы работы вам понравились?
На каком этапе урока вы испытывали затруднения?
Где вы видите практическое применение изученных теорем?
Оцените полезность донного урока для вас.
0
1
2
3
4
5
14.
14Среди наук из всех главнейших
Важнейшая всего одна.
Учите геометрию, она глава наукам,
Для жизни очень всем нужна.
Спасибо за урок!













 Математика
Математика








