Движение в пространстве

1. Движение в пространстве

2. 1. Центральная симметрия

3. Движение пространства – это отображение пространства на себя, сохраняющее расстояние между точками.

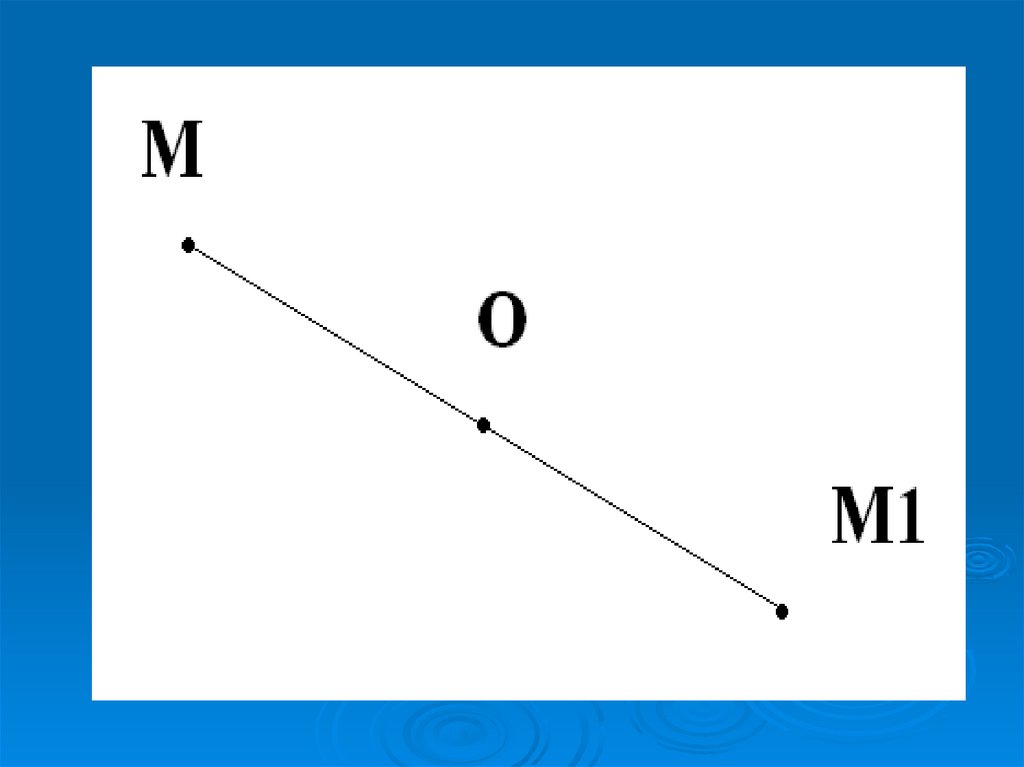
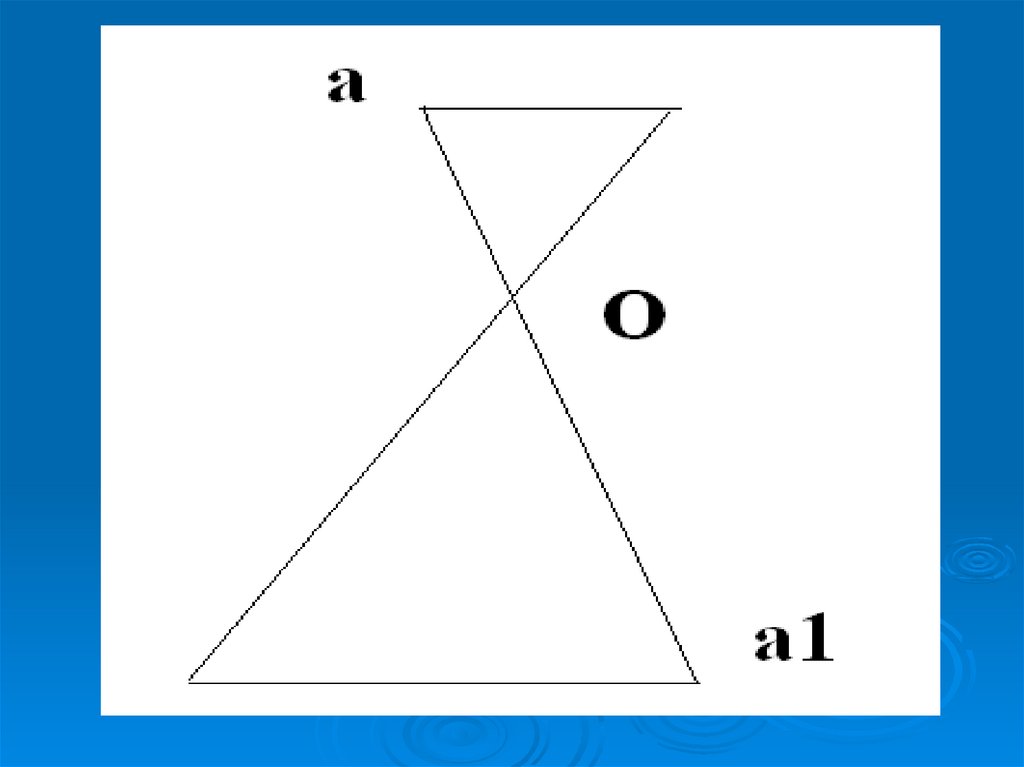
4. Центральная симметрия – отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1

относительно
данного центра О.

5.

6. 2. Осевая симметрия

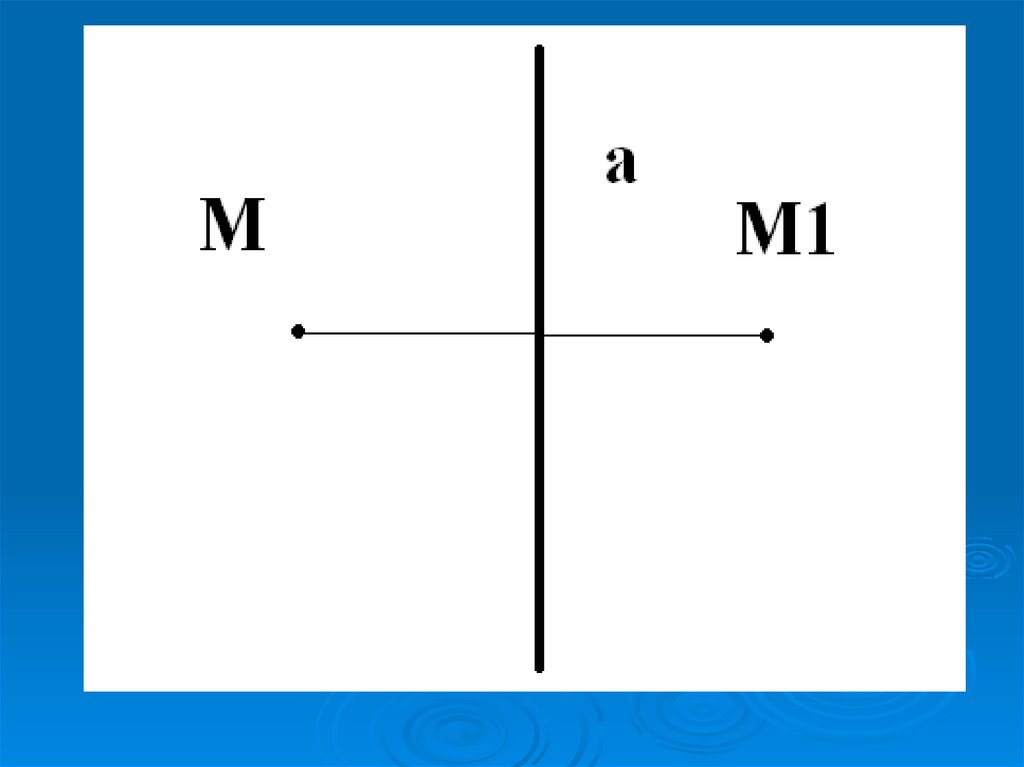
7. Осевой симметрией с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в

симметричную ей
точку М1 относительно оси а.

8.

9. 3. Зеркальная симметрия

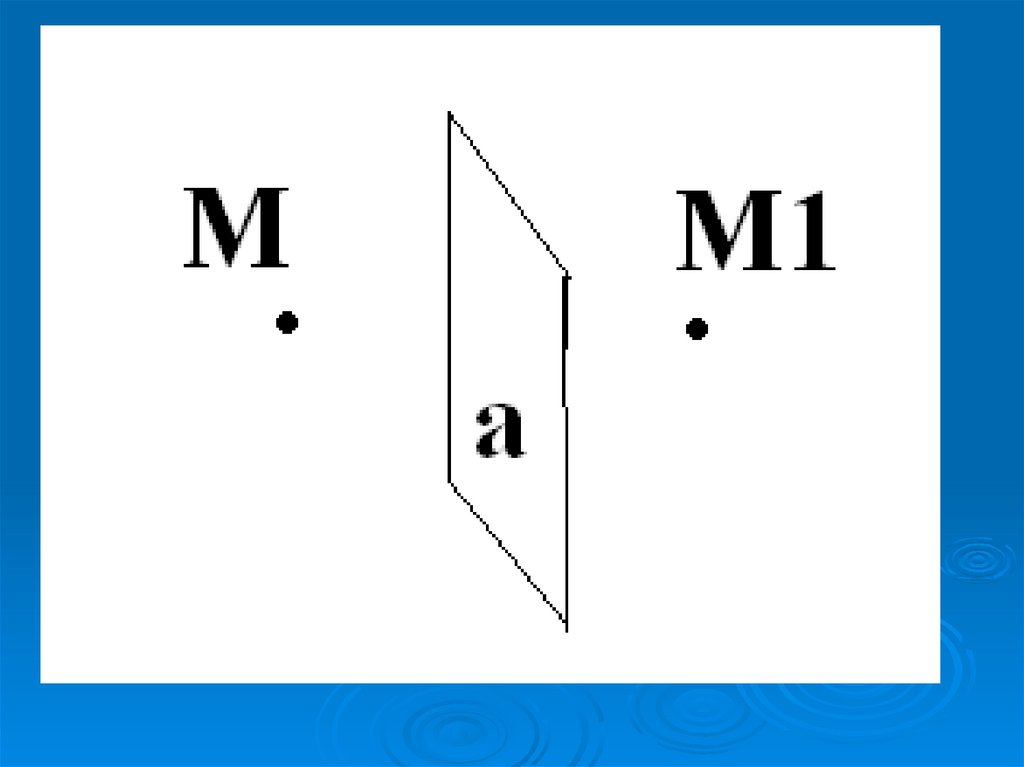
10. Зеркальной симметрией (симметрией относительно плоскости α) называется такое отображение пространства на себя, при котором

любая точка
М переходит в симметричную
ей относительно плоскости α
точку М1

11.

12. 4. Параллельный перенос

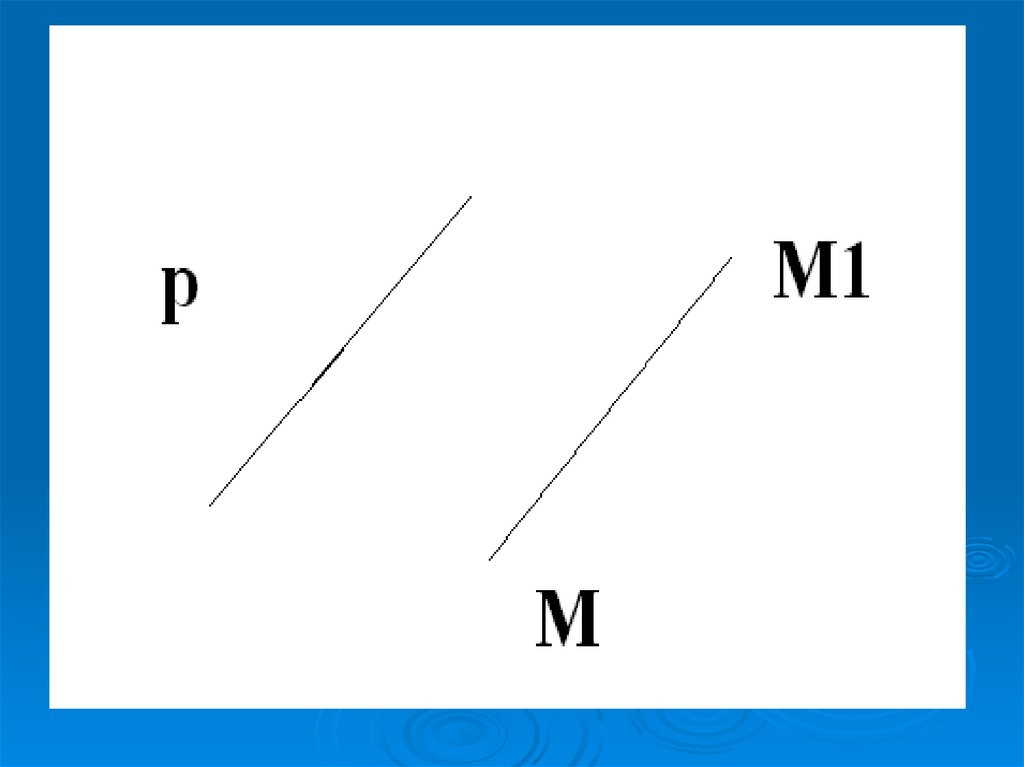
13. Параллельным переносом на вектор р называется отображение пространства на себя, при котором любая точка М переходит в такую

точку М1,
что ММ1= р

14.

15. 5. Преобразование подобия

16. Центральным подобием с центром О и коэффициентом k≠0 называется отображение пространства на себя, при котором каждая точка М

переходит в такую точку М1,
что ОМ1=kОМ