Похожие презентации:
Погрешности вычислений и алгоритмов
1.
ПОГРЕШНОСТИ ВЫЧИСЛЕНИЙ ИАЛГОРИТМОВ
Погрешности вычислений.
Устойчивость и сложность алгоритма.
Классификация погрешностей.
Абсолютная и относительная
погрешности числа и функции.
Прямая и обратная задачи теории
погрешностей.
Неустойчивые алгоритмы.
Особенности цифровой математики.
1
2.
ЗАДАЧИ КЛАССИЧЕСКОЙМАТЕМАТИКИ
Установить существование и
единственность решения.
Недостатки:
Невозможность решения поставленной
задачи;
Невозможность практического
использования полученного решения
(полученное решение громоздко).
2
3.
ЗАДАЧИ ВЫЧИСЛИТЕЛЬНОЙМАТЕМАТИКИ
Найти решение с требуемой
точностью.
Достоинства:
Возможность получить решения с
разными точностями до получения
требуемого результата.
3
4.
ТРЕБОВАНИЯ К ВЫЧИСЛИТЕЛЬНЫМ(ЧИСЛЕННЫМ) МЕТОДАМ
Адекватность дискретной модели исходной
математической задаче:
устойчивость,
сходимость,
корректность.
Возможность реализации данной дискретной
модели на компьютере.
4
5.
ПОНЯТИЕ УСТОЙЧИВОСТИЧИСЛЕННОГО МЕТОДА
Определение 1:
Слова «устойчивый алгоритм» означают, что
чем точнее задаются числа для обработки, тем
точнее получается результат.
Определение 2:
Устойчивость алгоритма означает, что малым
отклонениям в исходных данных соответствуют
малые отклонения в результате (решении).
5
6.
ПОНЯТИЕ СХОДИМОСТИЧИСЛЕННОГО МЕТОДА
Определение 1:
Сходимость означает близость получаемого
численного решения задачи к истинному решению.
Определение 2:
Под сходимостью численного метода (алгоритма)
понимают способность метода приводить к
точному решению за конечное число шагов, с
любой заданной точностью при любых начальных
6
приближениях.
7.
ПОНЯТИЕ КОРРЕКТНОСТИЧИСЛЕННОГО МЕТОДА
Определение 1:
Задача называется поставленной корректно, если
для любых значений исходных данных из
некоторого класса ее решение существует,
единственно и устойчиво по исходным данным.
Иногда при решении корректно
поставленной задачи может оказаться
неустойчивым метод ее решения.
7
8.
ПОНЯТИЕ КОРРЕКТНОСТИЧИСЛЕННОГО МЕТОДА
Определение 2:
Численный алгоритм (метод) называется
корректным в случае существования и
единственности численного решения при любых
значениях исходных данных, а также в случае
устойчивости этого решения относительно
погрешностей исходных данных.
8
9.
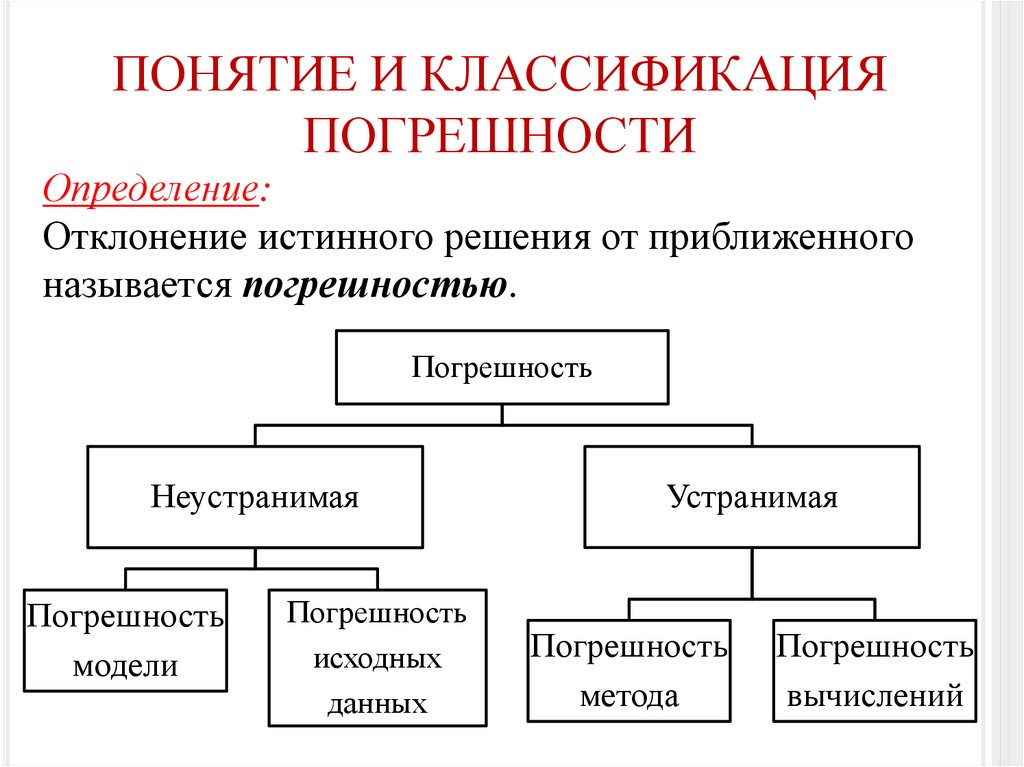
ПОНЯТИЕ И КЛАССИФИКАЦИЯПОГРЕШНОСТИ
Определение:
Отклонение истинного решения от приближенного
называется погрешностью.
Погрешность
Неустранимая
Погрешность
модели
Погрешность
исходных
данных
Устранимая
Погрешность
метода
Погрешность
9
вычислений
10.
ПОЛНАЯ ПОГРЕШНОСТЬПолная погрешность численного решения
включает:
Неустранимая погрешность:
погрешность постановки задачи,
неточность исходных данных;
Устранимая погрешность:
погрешность метода решения задачи,
погрешность вычислений.
10
11.
ПОЛНАЯ ПОГРЕШНОСТЬУстранимая погрешность может быть
уменьшена выбором более совершенного
(точного) метода и увеличением разрядности
вычислений.
11
12.
АБСОЛЮТНАЯ ПОГРЕШНОСТЬПриближенным числом Х* называется число,
незначительно отличающееся от точного Х и
заменяющее его в вычислениях.
Определение:
Пусть Х – точное решение задачи,
Х* – приближенное решение.
Тогда абсолютной погрешностью
приближенного числа Х* – называют величину
, которая является ограничением разности
|Х - Х*| ≤
12
13.
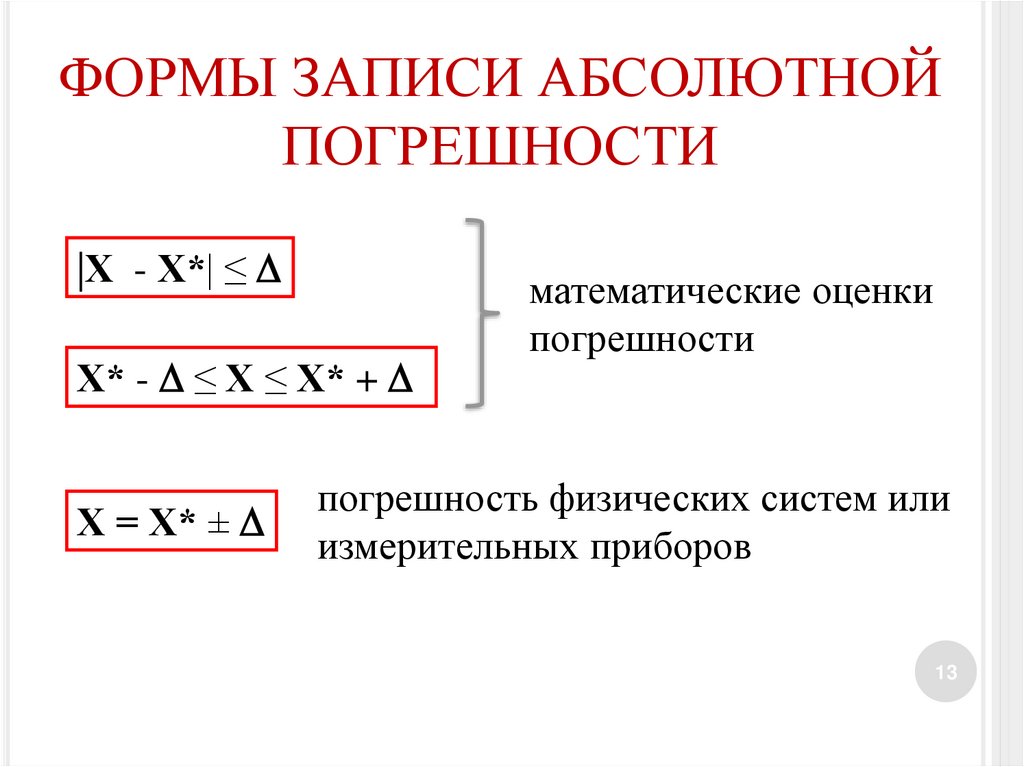
ФОРМЫ ЗАПИСИ АБСОЛЮТНОЙПОГРЕШНОСТИ
|Х - Х*| ≤
Х* - ≤ Х ≤ Х* +
Х = Х* ±
математические оценки
погрешности
погрешность физических систем или
измерительных приборов
13
14.
АБСОЛЮТНАЯ ПОГРЕШНОСТЬПример 1.1.
Пусть длина отрезка L = 100 см измерена с
точностью до 0.5 см.
Тогда пишут L = 100 см ± 0.5 см.
Здесь абсолютная погрешность = 0.5 см, а точная
величина длины L отрезка заключена в границах
99.5 см < L< 100.5 см.
В записи числа, полученного в результате
измерения, обычно указывают его
абсолютную погрешность.
14
15.
АБСОЛЮТНАЯ ПОГРЕШНОСТЬПример 1.2.
Определить абсолютную погрешность приближенного
числа Х* =3.14, заменяющего число .
Решение:
Так как 3.14 < < 3.15, то | Х*– Х | < 0.01;
Следовательно, можно принять = 0.01.
Однако, если учесть другое представление числа
3.14 < < 3.142,
то будем иметь лучшую оценку: = 0.002.
15
16.
АБСОЛЮТНАЯ ПОГРЕШНОСТЬВыводы:
Возможно существование несколько значений
абсолютной погрешности, каждое из которых
определяется границами приближенного
числа;
Абсолютная погрешность не является
достаточной характеристикой точности
измерения или вычисления.
16
17.
ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬОпределение:
Относительной погрешностью
приближенного числа Х* – называют величину
, определяемую выражением
Другая форма записи: X*(1 – δ) ≤ X ≤ X*(1 + δ)
17
18.
ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬБолее популярно в инженерных и
технических приложениях выражение
относительной погрешности в процентах.
Считается допустимой погрешность 3–5 % (в
отдельных задачах до 10%)
18
19.
ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ19
20.
ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬПример 1.4.
Найти относительные погрешности длин
измеренных отрезков а) L1 = 50.8 см ± 0.5 см
б) L2 = 3.6 см ± 0.5 см
Решение:
а)
б)
Х*
50.8
3.6
0.5
0.5
0,5
100% 0,984%
50,8
0,5
3,6
100% 13,888%
При одинаковой абсолютной погрешности =0.5,
относительные погрешности измерения отрезков
L1 и L2 существенно отличаются.
20
21.
СПОСОБЫ ПРЕДСТАВЛЕНИЯВЕЩЕСТВЕННЫХ ЧИСЕЛ
Представление в форме с фиксированной запятой:
1 – первая значащая цифра;
– основание системы счисления (2,8,10,16) или
основание позиционной системы;
0 i – числа из базисного набора.
21
22.
СПОСОБЫ ПРЕДСТАВЛЕНИЯВЕЩЕСТВЕННЫХ ЧИСЕЛ
В ЭВМ чаще всего используют представление
чисел в форме с плавающей запятой:
– основание системы счисления;
р – порядок числа (целое число,
положительное, отрицательное или нуль);
М – мантисса числа, –1<М<1
22
23.
СПОСОБЫ ПРЕДСТАВЛЕНИЯВЕЩЕСТВЕННЫХ ЧИСЕЛ
Пример 1.5.
Провести разложение числа 2.718 в форме с
фиксированной и плавающей запятой.
С фиксированной запятой:
2.718 = 2 100 + 7 10–1 + 1 10–2 + 8 10–3
=10; 1=2; 2=7; 3=1; 4=8;n=0.
С плавающей запятой:
2,718 = 0,2718 101
М=0.2718; р=1.
23
24.
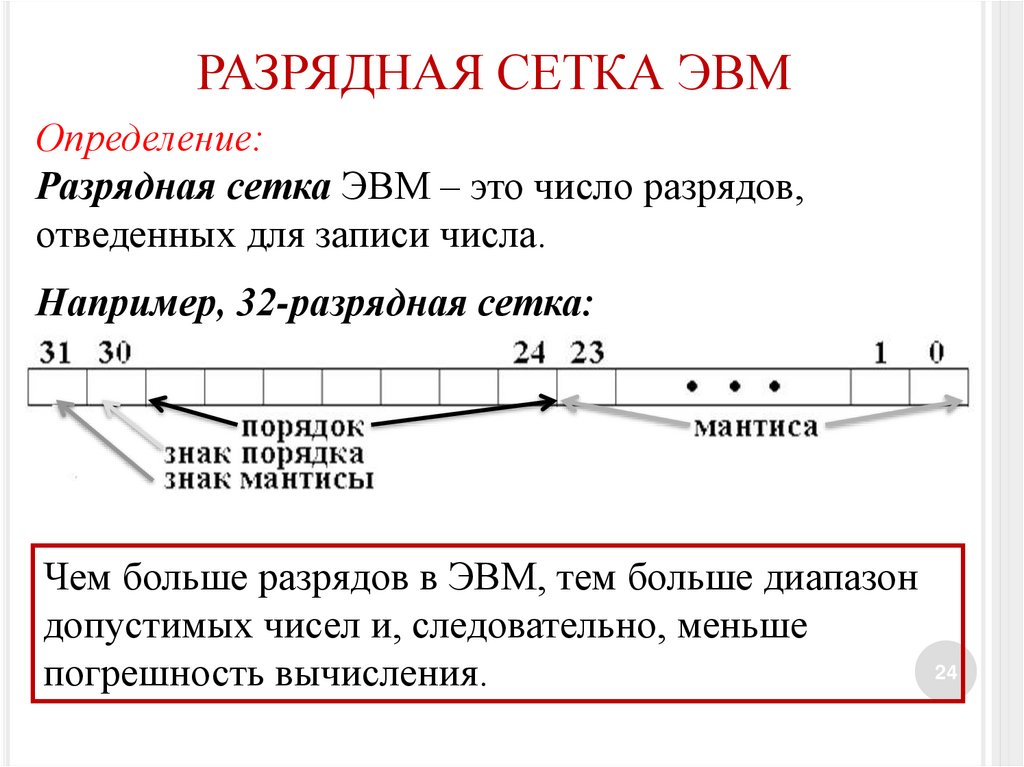
РАЗРЯДНАЯ СЕТКА ЭВМОпределение:
Разрядная сетка ЭВМ – это число разрядов,
отведенных для записи числа.
Например, 32-разрядная сетка:
Чем больше разрядов в ЭВМ, тем больше диапазон
допустимых чисел и, следовательно, меньше
24
погрешность вычисления.
25.
ТОЧНОСТЬ ВЫЧИСЛЕНИЙТочность вычислений определяется
количеством цифр результата, заслуживающих
доверия.
Характеристиками доверия к цифрам
результата являются:
значащие,
верные,
сомнительные цифры.
25
26.
ЗНАЧАЩИЕ, ВЕРНЫЕ,СОМНИТЕЛЬНЫЕ ЦИФРЫ
Определение:
Значащими цифрами числа Х* называют все
цифры в его записи, начиная с первой ненулевой
слева.
Определение:
Значащая цифра к считается верной, если
выполняется неравенство:
0.5 <1 (чаще всего в расчетах = 0.75)
26
в противном случае – к – сомнительная цифра.
27.
ЗНАЧАЩИЕ, ВЕРНЫЕ,СОМНИТЕЛЬНЫЕ ЦИФРЫ
Пример 1.6.
Определить число верных знаков в записи числа
x =2,718 0,001.
n k 1
Решение.
Х*=2,718;
Представим погрешность
=0,001= 0,1 10–2 (в форме с плавающей запятой)
2.718 = 2 100 + 7 10–1 + 1 10–2 + 8 10–3
n=0 .
Выберем =0,75.
27
28.
ЗНАЧАЩИЕ, ВЕРНЫЕ,СОМНИТЕЛЬНЫЕ ЦИФРЫ
Получим
n k 1
0,1 10–2 0,75 10 0–k+1
где k - неизвестное.
Равенство оснований (10) и числа мантиссы
(0,1<0,75) позволяют перейти к неравенству
относительно показателей:
–2 < 1–k Отсюда k 3
Таким образом:
Верными цифрами числа являются три первые
28
значащие цифры, т.е. 2,71;
Цифра 8 – сомнительная.
29.
ОБЩАЯ ФОРМУЛА ПОГРЕШНОСТИОбщая погрешность результата определяется:
величинами отдельных погрешностей,
видом математического выражения.
Правила трансформации погрешностей:
Абсолютная погрешность суммы конечного
числа приближенных чисел не превышает суммы
абсолютных погрешностей этих чисел.
Относительная погрешность произведения
конечного числа приближенных чисел не
превышает суммы относительных погрешностей 29
этих чисел.
30.
.,
ОБЩАЯ ФОРМУЛА ПОГРЕШНОСТИ
Пусть задана функция Z=f(x1, х2, …, хn)
Известны абсолютные (или относительные)
погрешности аргументов х1, х2,…, хn ( х1, х2,…,
хn).
Z
Абсолютная погрешность функции: Z
xi
i 1 xi
n
Относительная погрешность: Z x i
ln Z x i
x i
30
i 1
n
31.
ОБЩАЯ ФОРМУЛА ПОГРЕШНОСТИЕсли сложная функция Z зависит только от двух
аргументов, т.е. Z=f(x, y), то:
Абсолютная
погрешность
Относительная
погрешность
x y x y
x x y y
x y
x y
x y x y y x
x y x y
x y x x y
y
y2
x
x y
y
x m m x m 1 x
x m m x
31
32.
ОБЩАЯ ФОРМУЛА ПОГРЕШНОСТИПример 1.7.
Вычислить абсолютную и относительную
погрешности сложной функции
при заданных значениях
a = 0.643 ± 0.005
b = 2.17 ± 0.02
c = 5.843 ± 0.01
a* = 0.643
b* = 2.17
c* = 5.843
a b3
Z
c
а =0,005
b =0,02
c =0,01
Относительные погрешности найдем как:
а =0,777;
b =0,922;
100
x*
c =0,171.
32
33.
ОБЩАЯ ФОРМУЛА ПОГРЕШНОСТИРешение.
Вычислим значение приближенного числа Z*, подставив
значения входящих в него аргументов a*, b*, c*.
a b
Z
c
3
0,643 2,173
Z
2,71814
5,843
*
u
3
Z u v (a b ) ( c )
v
1
(a) 3 (b) (c)
2
33
34.
ОБЩАЯ ФОРМУЛА ПОГРЕШНОСТИПодставим значения относительных погрешностей
аргументов
1
Z (a ) 3 (b) (c)
2
1
0.777 3 0.921 0.171 3.628 (%)
2
Z Z * 3.628 2.718
Z
0.986
100
100
34
35.
ОБЩАЯ ФОРМУЛА ПОГРЕШНОСТИПример 1.8.
Вычислить значение аналитического выражения и
оценить абсолютную и относительную погрешности
сложной функции
при заданных значениях
a = 0.643 ± 0.0005
b = 2.17 ± 0.002
c = 5.843 ± 0.001
35
36.
ОБЩАЯ ФОРМУЛА ПОГРЕШНОСТИРешение.
Вычислим значение приближенного числа Z*,
подставив значения входящих в него аргументов a, b, h.
Z * 0,8307
Абсолютные погрешности из условия задачи равны
а =0,04; b =0,02; h =0,01.
Относительные погрешности найдем как:
а =3,5057 %;
b =0,6337 %;
h =0,8772 %.
36
37.
ОБЩАЯ ФОРМУЛА ПОГРЕШНОСТИВ данной сложной функции Z* основная
математическая операция сложение.
Воспользуемся формулой для вычисления абсолютной
погрешности, предварительно упростив первое
слагаемое функции:
a b
2
Z
(a b )
h
2 a ( a b)
Z
2 h h
2
(a b )
Подставив численные значения абсолютных
погрешностей, получим:
Относительную погрешность функции пересчитаем
37
по формуле


































 Математика
Математика








