Цифровая обработка изображений. Лекция 3. Фильтрация шумов

1. Цифровая обработка изображений

Лекция 3
Фильтрация шумов

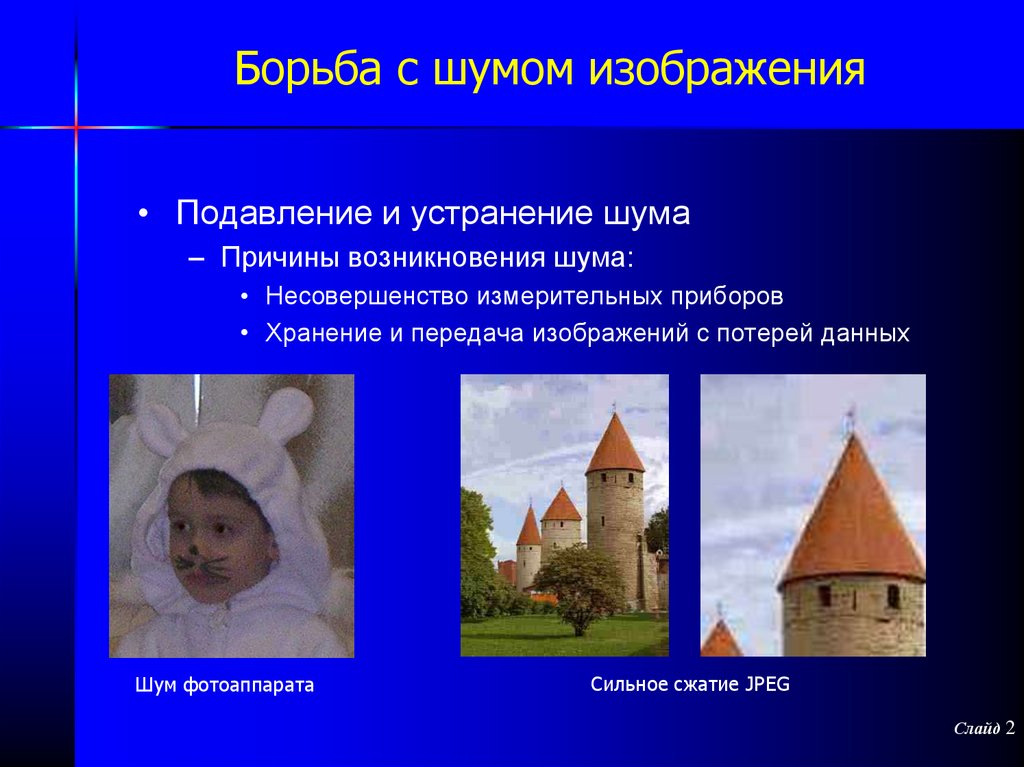
2. Борьба с шумом изображения

• Подавление и устранение шума
– Причины возникновения шума:
• Несовершенство измерительных приборов
• Хранение и передача изображений с потерей данных
Шум фотоаппарата
Сильное сжатие JPEG
Слайд 2

3. Подавление и устранение шума

– Усреднение (box filter)
– Медианный фильтр
– Математическая морфология
– Фильтр Гаусса (gaussian blurring)
– Адаптивные фильтры
– И другие методы
Слайд 3

4. Шум в бинарных изображениях

Пример бинарного изображению с сильным шумом
Слайд 4

5. Подавление и устранение шума

Устранение шума в бинарных изображениях
Бинарное изображение – изображение, пиксели
которого принимают всего два значения (0 и 1).
Широко известный способ - устранение шума с
помощью операций математической морфологии:
Сужение (erosion)
Расширение (dilation)
Закрытие (closing)
Раскрытие (opening)
Слайд 5

6. Reducing Noise in Binary Images

Noise can appear in several forms
- isolated pixels of the opposite value salt-and-pepper noise
(a)
- small holes in objects/small spots on background areas (b)
- distinct lines merging and single lines splitting (a,b)
- contour protrusions and intrusions (c)
Слайд №6

7. Reducing Noise in Binary Images

Logical masks
- simplest form of noise reduction
- tuned by hand to specific situations
- logical tests are performed on the neighbourhood of pixel
aij, the value of aij may be changed as a result
- e.g. change aij if the number of black/white pixels in the 8
pixels surrounding aij (its 8-neighbourhood) is above some
threshold
Слайд №7

8. Reducing Noise in Binary Images

Many (more principled) techniques are based upon the Distance Transform
and/or Mathematical Morphology
Distance transforms estimate the gap between each pixel in one set, e.g. B
(black pixels) and the nearest pixel in another set, e.g. W (white)
The resulting grey level image is known as a distance map
The distance map can be computed for both B and W, W pixels are
usually assigned negative distance values
Any distance measure can be
chosen, Euclidean distance is
ideal but expensive so digital
approximations (e.g. city block)
distance are commonly used
-3
-2
-2
-2
-2
-2
-2
-3
-3
-2
-2
-1
-1
-1
-1
-2
-2
-3
-2
-1
-1
1
1
-1
-1
-2
-2
-2
-1
1
1
1
1
-1
-1
-2
-2
-1
1
2
2
1
1
-1
-2
-2
-1
1
1
2
1
1
-1
-2
-2
-1
-1
1
1
1
-1
-1
-2
-2
-2
-1
-1
1
-1
-1
-2
-2
-3
-2
-2
-1
-1
-1
-2
-2
-3
-3
-3
-2
-2
-2
-2
-2
-3
-3
Слайд №8

9. Reducing Noise in Binary Images

Simultaneous application of DTs to black and white pixels allows
object protrusions and intrusions can be removed at the same time
- compute distance map for both object (+ve) and background (-ve)
- apply (separate) thresholds to the object and background regions
of the distance map: set sub-threshold pixels to 0. This will create a
channel of 0s between +ve and –ve regions
- apply a reverse distance transform, propagating distance
information into the zero channel
Слайд №9

10. Reducing Noise in Binary Images of Line Drawings

Distance Transforms (or morphology) can be used both to smooth
boundaries and remove salt-and-pepper noise (a, b below)
Distance transforms (or morphology) can also remove small holes,
though the amount of smoothing needed to remove the blob and hole
in b (below) may distort other areas of the image
Logical masks can be targeted, avoiding widespread effects (b,c)
Given medium-sized noise regions, logical tests may be applied to a
contour description
Слайд №10

11. Усреднение (усредняющий фильтр)

Операция усреднения значения каждого пикселя –
cвертка по константной функции:
n
m
1
I (i, j ) I (i l )( j k )
4nm
l n k m
Результат применения:
Слайд 11

12. Медианный фильтр

Устранение шума в полутоновых, цветных и бинарных
изображениях с помощью медианного фильтра - выбор
медианы среди значений яркости пикселей в некоторой
окрестности.
Определение медианы:
Ai , i 1,n; - отсортированный набор чисел,
A n / 2 медиана набора.
Медианный фильтр радиусом r – выбор медианы среди
пикселей в окрестности [-r,r].
Слайд 12

13. Медианный фильтр

Результат применения медианного фильтра с радиусом 5 пикселей.
Результат применения медианного фильтра с радиусом в 7 пикселей
к изображению с шумом и артефактами в виде тонких светлых
окружностей.
Слайд 13

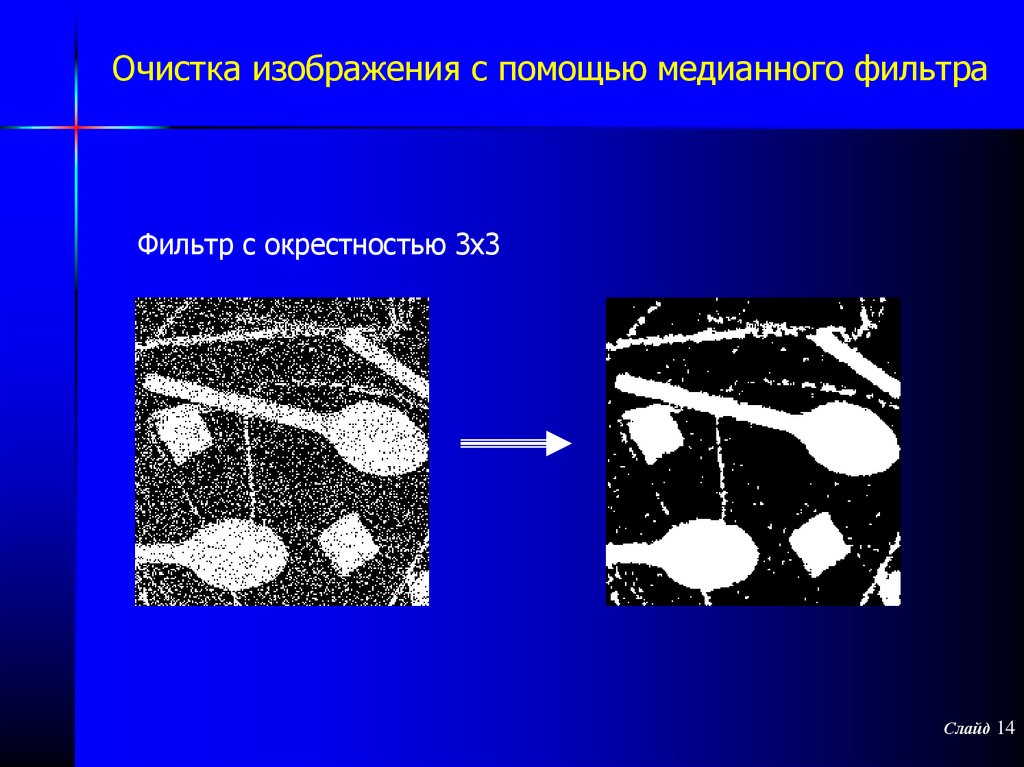
14. Очистка изображения с помощью медианного фильтра

Фильтр с окрестностью 3x3
Слайд 14

15. Быстрая реализация медианного фильтра

Медианный фильтр считается дольше, чем операция
свертки, поскольку требует частичной сортировки
массива яркостей окрестных пикселей.
Возможности ускорения:
• Использовать алгоритмы быстрой сортировки
• Конкретная реализация для каждого радиуса (3x3,
5x5)
• Не использовать сортировку вообще – считать
через гистограмму окрестности точки
Слайд 15

16. Как бороться с шумом аппаратуры?

Предположим, камера, которой производится съемка
заметно «шумит». Обычно шум измерительной
аппаратуры моделируется как случайная нормально
распределенная случайная величина с нулевым
средним - Err(i,j) ;
I (i, j ) g r (i, j ) Err (i, j );
1 N
I (i, j ) I k (i, j );
N k 1
E ( I (i, j )) g r (i, j );
Слайд 16

17. Примеры шумоподавления

Зашумленные изображения
Усреднение по 10
изображениям
Слайд 17

18. Примеры шумоподавления

Исходное изображение
Испорченное
изображение
Слайд 18

19. Примеры шумоподавления

Усреднение по 9
пикселям (3x3)
Медианный фильтр
(3x3)
Слайд 19

20. Устранение шума в полутоновых и цветных изображениях

Пример: изображение с равномерным шумом.
I (i, j ) gr (i, j ) Err (i, j )
Err(i,j) – нормально распределенная случайная
величина.
Слайд 20