Похожие презентации:
Геометрические основы теории построения линейной перспективы. Проецирующий аппарат и его элементы. Лекция №6
1.
ЛЕКЦИЯ №6Геометрические основы теории
построения линейной перспективы.
Проецирующий аппарат и его элементы.
Перспектива точки
2.
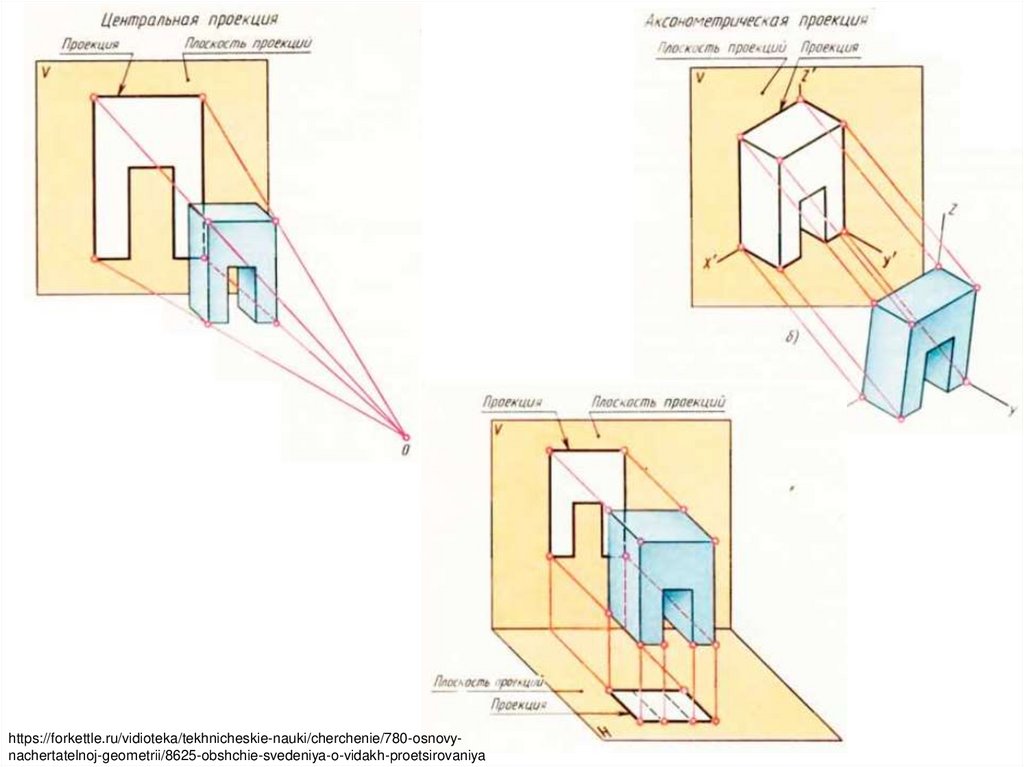
https://forkettle.ru/vidioteka/tekhnicheskie-nauki/cherchenie/780-osnovynachertatelnoj-geometrii/8625-obshchie-svedeniya-o-vidakh-proetsirovaniya3.
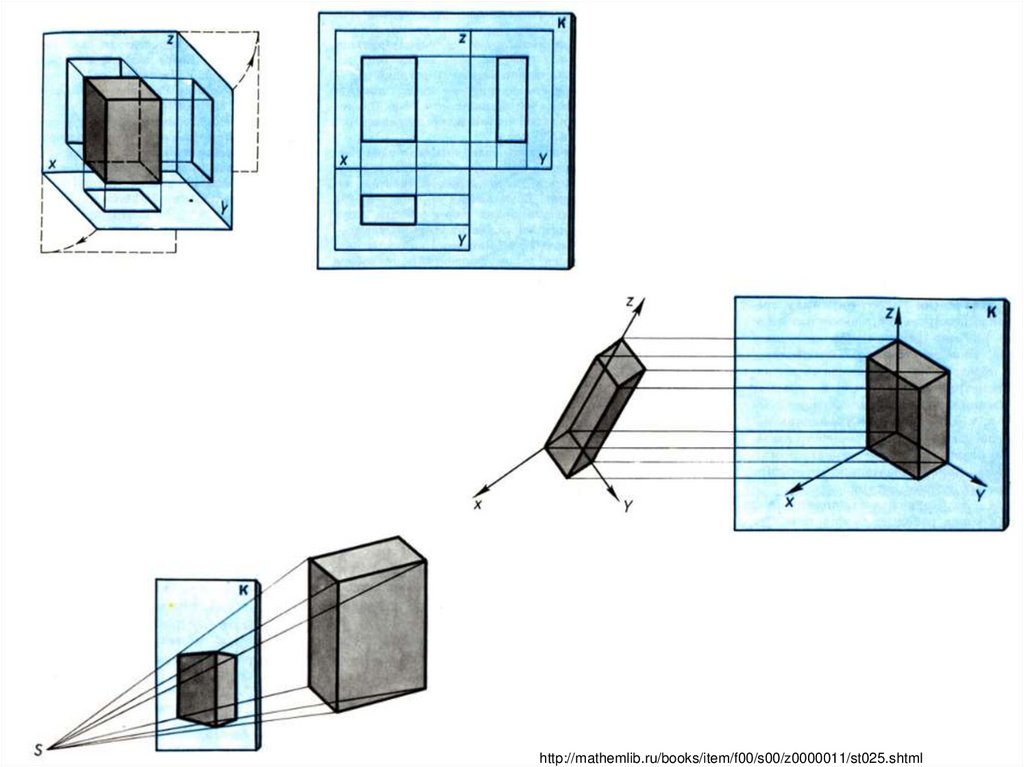
http://mathemlib.ru/books/item/f00/s00/z0000011/st025.shtml4.
Перспектива как наука возникла в глубокой древности в связи с необходимостьюизображать на плоскости предметы в трехмерном пространстве и развивалась в двух
направлениях: в области науки (строительстве, технике) и в живописи.
История свидетельствует, что величайшие сооружения Древней Греции и Рима были
построены по изображениям – прототипам современных чертежей. Начала геометрии, в
частности перспективы, можно встретить в трудах древнегреческих и римских ученых:
Эсхила (525-456 гг. до н.э.); Демокрита (около 460-370 гг. до н.э.); древнегреческого
ученого и математика Эвклида (300 лет до н.э.). Закономерностями построения
изображений окружающей действительности, близкой к зрительному восприятию,
занимались художники.
Основоположником перспективы как науки считают итальянского теоретика
искусства, архитектора и художника эпохи возрождения Филиппо Брунеллески (13771446), который применил правила перспективы
в изображении архитектурных
сооружений.
Большой вклад в теорию перспективы внес гениальный итальянский художник и
ученый Леонардо да Винчи (1452-1519). В «трактате живописи» он изложил также
правила перспективы. Леонардо да Винчи считал, что перспектива относится к
«механическим наукам», которыми не должен пренебрегать ни один художник.
Способ построения в перспективе предметов с помощью координат был предложен
французским архитектором, инженером и математиком Жираром Дезаргом (1593-1662),
который тем самым положил начало методу аксонометрических проекций.
5.
Альберти Леон Баттиста (1404-1472) – итальянский философи архитектор, сформулировал основы теоретической перспективы.
Леонардо да Винчи (1452-1519) – итальянский художник и ученый,
дополнил линейную перспективу учением «об уменьшении
цветов и отчетливости очертаний», что позволило ему получать
удивительно рельефные реалистичные изображения.
Альбрехт Дюрер (1471-1528) – немецкий математик, художник
и гравер, высказывал идеи об ортогональном проецировании
пространственных
фигур на плоскость, разработал метод
ортогонального изображения конических сечений и способ
построения
перспективы по двум ортогональным проекциям
предмета.
Гвидо Убальди (1545-1607) – итальянский ученый, считается
основателем теоретической перспективы. В его работах содержится
решение почти всех основных задач перспективы.
Жирар
Дезарг
(1593-1662) – французский
архитектор и
математик, применил для построения перспективы метод
координат, обосновал теорию аксонометрических проекций.
6.
7.
Перспективой (перспективной проекцией) называетсяцентральная проекция предмета на специально
выбранную поверхность. Перспектива происходит от
латинского глагола "perspicere" − видеть насквозь.
Перспектива является одним из методов построения
наглядных изображений пространственных предметов,
которые широко используются в инженерной графике и
особенно в архитектурно-строительном черчении.
8.
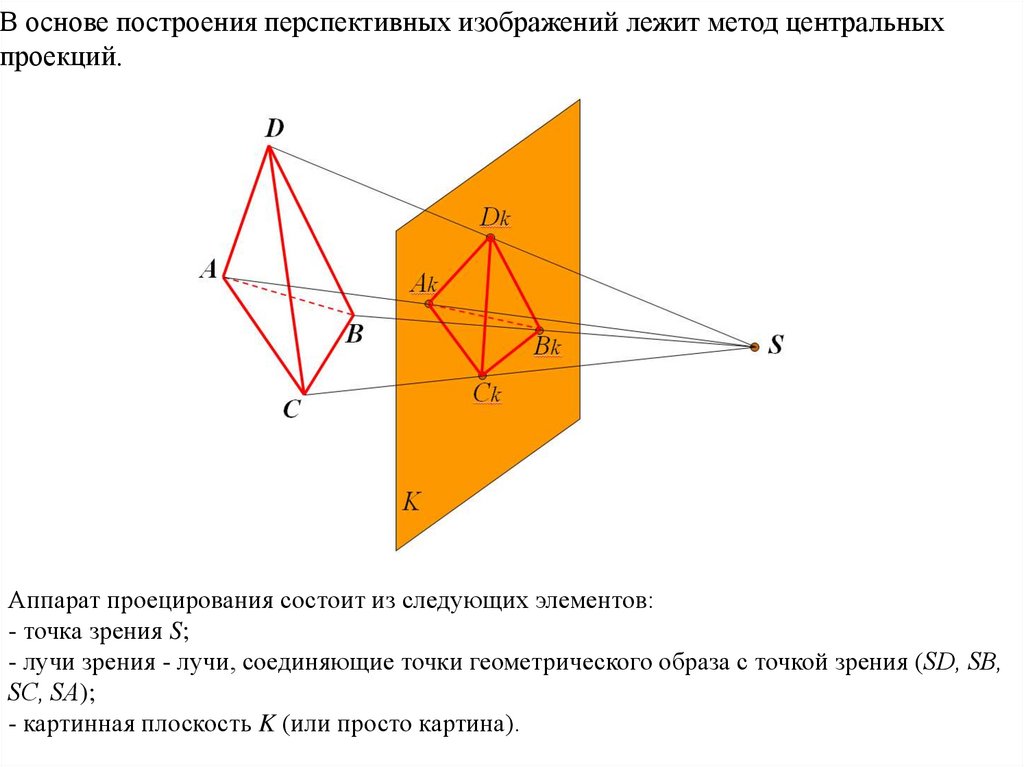
В основе построения перспективных изображений лежит метод центральныхпроекций.
Аппарат проецирования состоит из следующих элементов:
- точка зрения S;
- лучи зрения - лучи, соединяющие точки геометрического образа с точкой зрения (SD, SВ,
SС, SА);
- картинная плоскость K (или просто картина).
9.
10.
Перспектива может быть построена различнымиспособами и на различных поверхностях (на плоскости,
на поверхностях цилиндра, шара и т.д.).
Основные виды перспективных изображений:
1) линейная перспектива - перспектива предмета,
построенная на вертикальной плоскости. Это один из
самых простых и наиболее распространенных видов
перспективных изображений;
2) плафонная перспектива − перспектива предмета,
построенная на горизонтальной плоскости;
3) панорамная перспектива – перспектива предмета,
построенная на внутренней поверхности цилиндра;
4) купольная перспектива - перспектива предмета,
построенная на внутренней поверхности сферы.
11.
Линейная перспектива. Аппарат линейной перспективыПредставить себе перспективные изображения несложно. Если смотреть на предмет
через стеклянное окно и обвести тушью на стекле всё увиденное, получим перспективу,
причем глаз человека здесь является центром проекции S, а стекло – картинной
плоскостью К (рис. 2.1). Это – так называемая линейная перспектива (построение
изображений на вертикальной плоскости).
https://studme.org/228266/informatika/osnovnye_svoystva_perspektivnoy_proektsii
12.
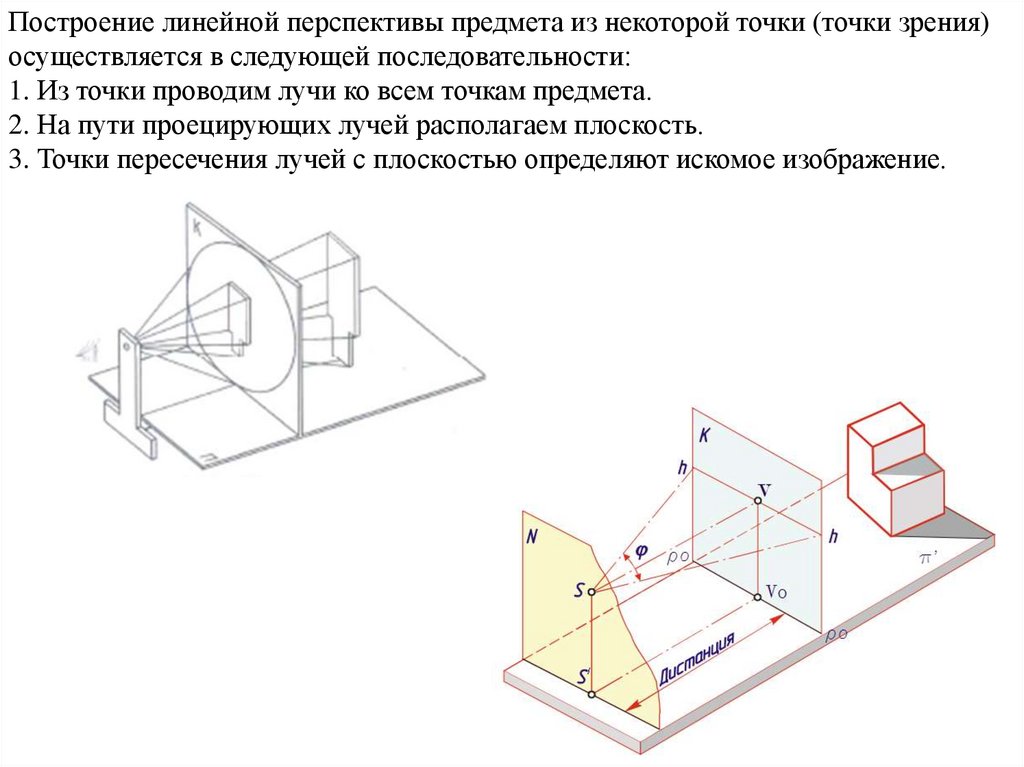
Построение линейной перспективы предмета из некоторой точки (точки зрения)осуществляется в следующей последовательности:
1. Из точки проводим лучи ко всем точкам предмета.
2. На пути проецирующих лучей располагаем плоскость.
3. Точки пересечения лучей с плоскостью определяют искомое изображение.
13.
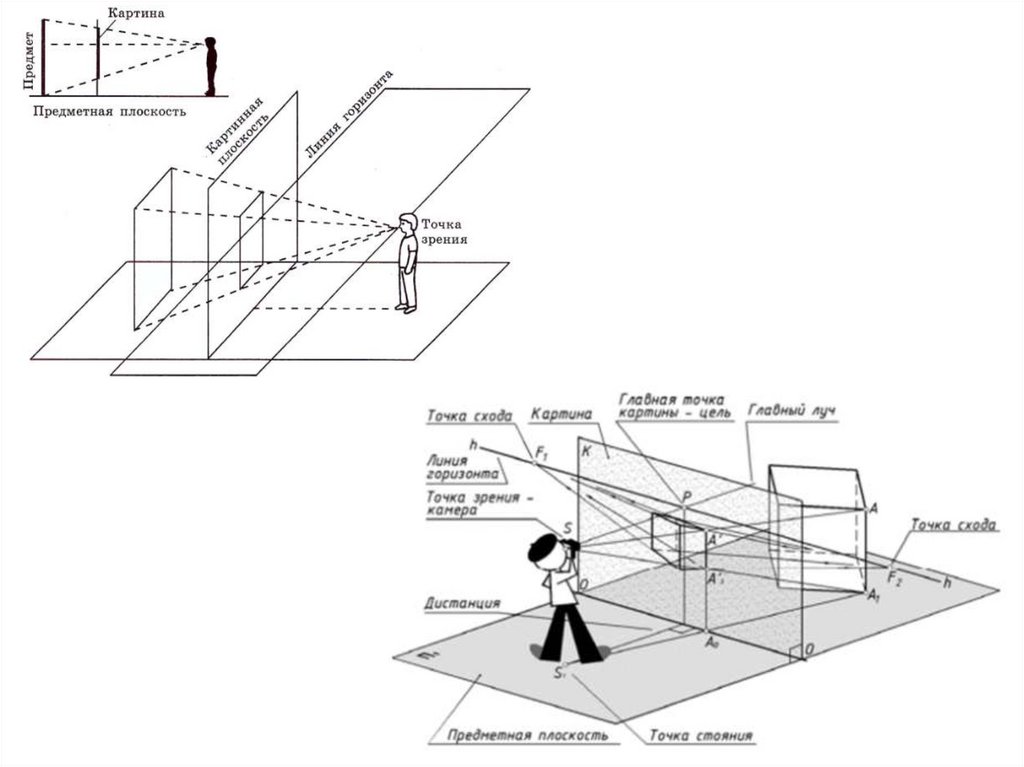
Основные элементы перспективы:π' - предметная плоскость – горизонтальная плоскость, на которой располагается
изображаемый предмет;
К - картинная плоскость (картина) – вертикальная плоскость, на которой строится
перспективная проекция предмета. Она располагается перпендикулярно к предметной
плоскости π'. Линия ρо – линия пересечения картины с предметной плоскостью называется
основанием картины;
S – точка зрения – точка пространства, через которую проходят проецирующие лучи,
определяет положение глаз зрителя. Ортогональная проекция S' точки зрения на
предметную плоскость называется точкой стояния;
V - главная точка картины – основание перпендикуляра SV, опущенного из точки зрения
S на картину К, где SV – главный луч картины, V’ - основание главной точки;
h - линия горизонта - линия пересечения горизонтальной плоскости, проходящей через
точку зрения S с картиной К;
φ – угол зрения;
плоскость N - нейтральная плоскость, проходящая через точку зрения параллельно
картине.
ρо – основание картины – линия пересечения предметной и картинной плоскостей
14.
Картинная и нейтральная плоскости делят все пространство на три части:мнимое, промежуточное и предметное пространство.
15.
ПЕРСПЕКТИВА ТОЧКИЧтобы построить перспективу точки А, расположенной в
предметном пространстве, необходимо из точки S провести
проецирующий луч через точку А. Точка пересечения этого
проецирующего луча SA с картинной плоскостью К определит
перспективу точки А − А'.
Аналогично можно найти перспективу основания точки А − A'.
Точка A' называется перспективой основания точки А или
вторичной перспективной проекцией точки А (первичной
проекцией считается ортогональная проекция точки А).
16.
Точка является основным и простейшим геометрическим элементом пространства. Онаможет занимать по отношению к проецирующему аппарату как общее положение, т. е.
располагаться в предметном (мнимом, промежуточном) пространстве, так и частное
положение, т.е. лежать либо в предметной плоскости, либо в плоскости картины. На
рисунке задана точка А, расположенная в предметном пространстве двумя проекциями - Аn,
A'n.
Точка в пространстве задается, как правило, самой точкой Аn и ее проекцией на
предметную плоскость π' - A'n (основание точки А).
17.
Положение. Перспектива точки (А) и перспектива ее основания (А ) всегда лежатна одном перпендикуляре к основанию картины ρо.
Точка Аn расположена в предметном пространстве выше линии горизонта,
следовательно, ее перспектива А лежит выше линии h.
A
V
h
A'
Vo
ρo
18.
AA'
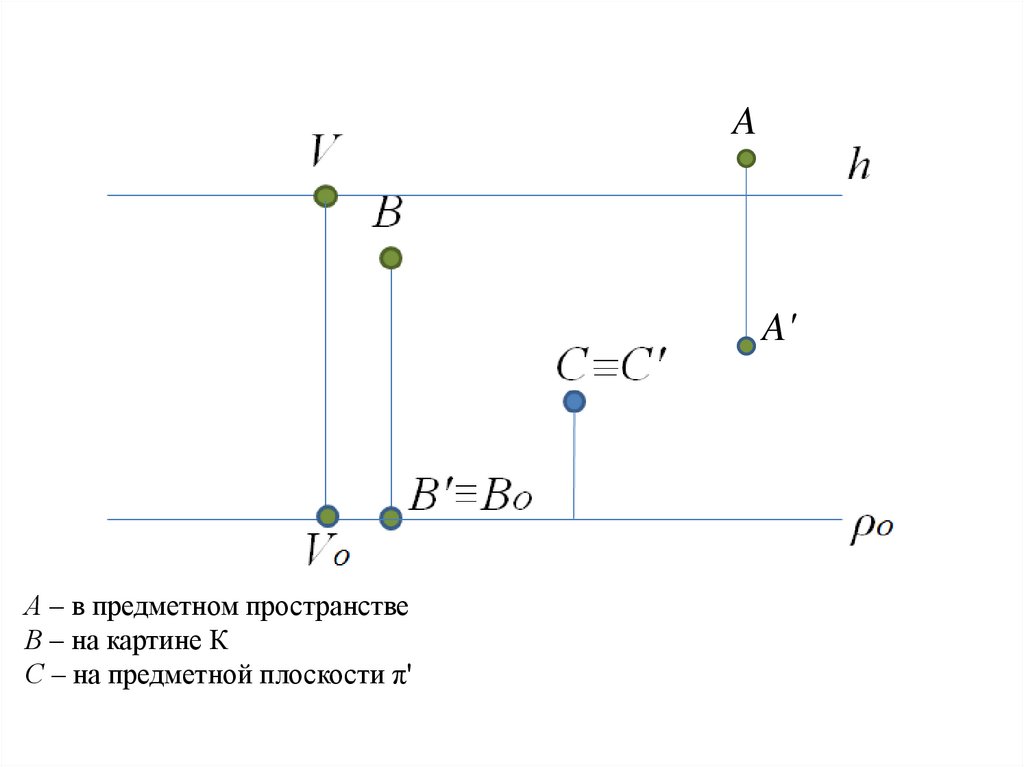
А – в предметном пространстве
В – на картине К
С – на предметной плоскости π'
19.
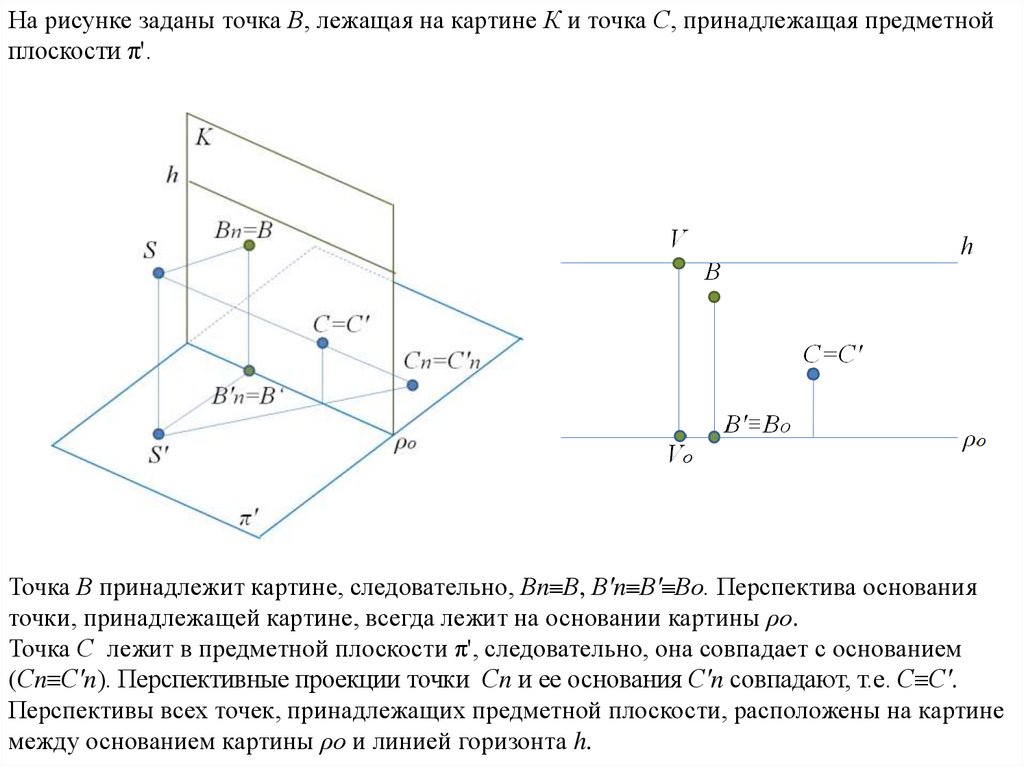
На рисунке заданы точка В, лежащая на картине К и точка С, принадлежащая предметнойплоскости π'.
Точка В принадлежит картине, следовательно, Вn В, В'n В' Во. Перспектива основания
точки, принадлежащей картине, всегда лежит на основании картины ρо.
Точка С лежит в предметной плоскости π', следовательно, она совпадает с основанием
(Сn С'n). Перспективные проекции точки Сn и ее основания С'n совпадают, т.е. С С'.
Перспективы всех точек, принадлежащих предметной плоскости, расположены на картине
между основанием картины ρо и линией горизонта h.












 Инженерная графика
Инженерная графика








