Геометрические основы теории теней

1. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

Направления обучения
«Архитектура»
«Реконструкция и реставрация архитектурного наследия»
«Дизайн архитектурной среды»
«Градостроительство»

2. Лекция 3

Солодухин Е.А., 2017

3.

Геометрические
основы теории теней

4.

• Освещение разделяют на естественное
(солнечное) и искусственное (факельное).
• При естественном освещении солнце
рассматривается как точечный источник
света, удаленный в бесконечность, и
поэтому световые лучи принимаются как
параллельные друг другу прямые.
• Естественное (солнечное) освещение
следует рассматривать как параллельное
косоугольное проецирование, у которого
центром проецирования является солнце
(для
нас
бесконечно
удаленная
несобственная точка).

5.

Основной геометрической задачей при построении
теней является определение границ собственных и
построение контуров падающих теней.

6.

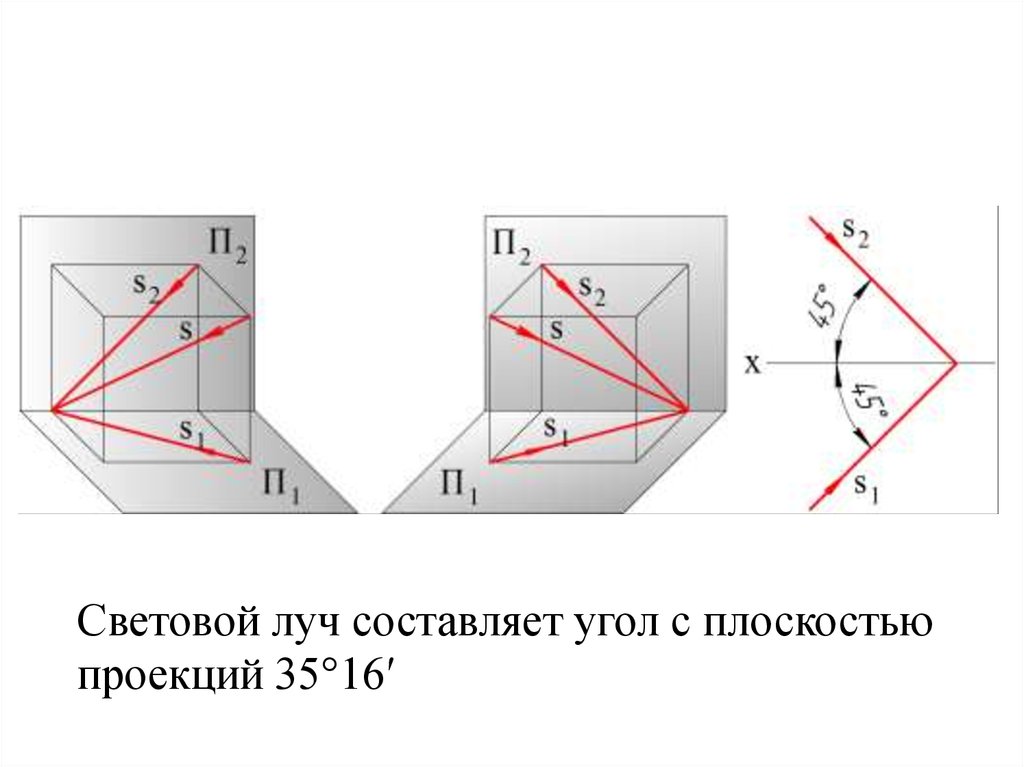
Световой луч составляет угол с плоскостью
проекций 35°16′

7. Тень от точки на плоскости проекций

8.

Тень от точки – точка пересечения светового луча,
проходящего через заданную точку, с поверхностью
(плоскостью проекций).
Рассматривается действительная (реальная) и условная (мнимая) тень.
Действительной тенью от точки является точка пересечения светового
луча, проходящего через заданную точку, с той поверхностью, которая
встречается на пути светового луча первой.

9.

По соотношению величин расстояний от горизонтальной и
фронтальной проекции точки до оси х12 , что соответствует
глубине и высоте точки, можно точно сказать на какой из
плоскостей проекций окажется действительная тень точки.

10.

Тень от прямой на
плоскости проекций

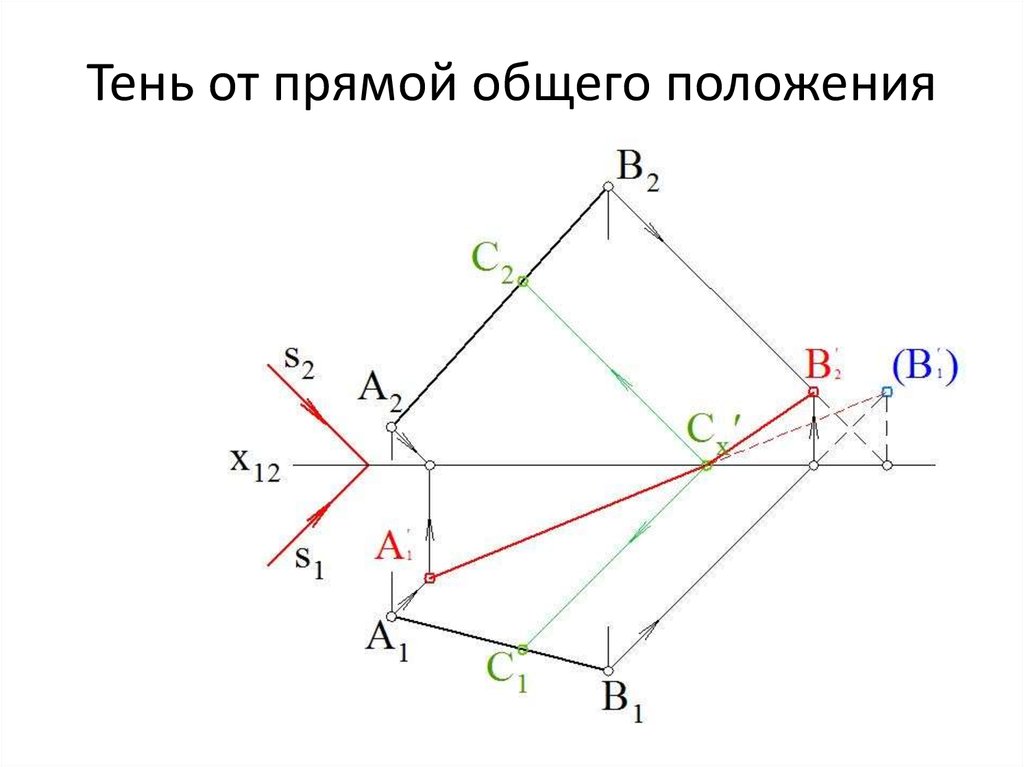
11. Тень от прямой общего положения

ТЕНЬ ОТ ПРЯМОЙ
ОБЩЕГО ПОЛОЖЕНИЯ

12.

Тень от прямой, в общем случае, – прямая

13. Тень от прямой общего положения

14. Тень от прямой частного положения

ТЕНЬ ОТ ПРЯМОЙ
ЧАСТНОГО ПОЛОЖЕНИЯ

15. Тень от прямой уровня

Если прямая параллельна плоскости (в т. ч. плоскости
проекций), то тень от нее на этой плоскости параллельна
самой прямой или ее ортогональной проекции на эту же
плоскость
m ‖ П1 (m′1 ‖ m) ˄ (m′1 ‖ m1) или m ‖ П2 (m′2 ‖ m) ˄ (m′2 ‖ m2)

16.

17. Тень от проецирующей прямой

Если прямая перпендикулярна плоскости (в т. ч. плоскости
проекций), то тень от нее на этой плоскости параллельна
ортогональной проекции светового луча на эту плоскость
m П1 m′1 ‖ s1 или m П2 m′2 ‖ s2

18.

19. Тень от плоской фигуры

ТЕНЬ ОТ ПЛОСКОЙ ФИГУРЫ