Случайные события. Вероятность события

1.

2.

Теория вероятностей –
это математическая
наука, которая изучает
закономерности в случайных
событиях.
Основные понятия: испытания
и события.

3.

В современном мире автоматизации
производства теория вероятности(Т.В)
необходима специалистам для
решения задач, связанных с
выявлением возможного хода
процессов, на которые влияют
случайные факторы(например, ОТК:
сколько бракованных изделий будет
изготовлено).

4.

Возникла теория
вероятностей в 17 веке в
переписке Б. Паскаля и
П.Ферма, где они
производили анализ
азартных игр.

5.

Советские и русские ученые
также принимали участие в
развитии этого раздела
математики: П.Л. Чебышев, А.А.
Марков, А.М. Ляпунов, А.Н.
Колмогоров

6.

Испытания(опыт)реализация данного комплекса
условий, в результате которого
непременно произойдет какоелибо событие.
Например, бросание монетыиспытание; появление герба
или цифры- события.

7.

Случайным событием
называется событие, связанное
с данным испытанием, которое
при осуществлении испытания
может произойти, а может и не
произойти.

8.

Вы выиграли в лотерею —
случайное событие. Пригласили
друзей отпраздновать выигрыш,
а они по дороге к вам застряли
в лифте — тоже случайное
событие. Правда, мастер оказался
поблизости и освободил всю
компанию через десять минут —
и это тоже можно считать
счастливой случайностью…

9.

Наша жизнь полна случайных
событий. О каждом из них можно
сказать, что оно произойдет
с некоторой вероятностью. Скорее
всего, вы интуитивно знакомы с этим
понятием. Теперь мы дадим
математическое определение
вероятности.

10.

Начнем с самого простого примера.
Вы бросаете монетку. Орел или
решка?
Такое действие, которое может
привести к одному из нескольких
результатов, в теории вероятностей
называют испытанием.
Орел и решка — два
возможных исхода испытания.
Орел выпадет в одном случае из двух
возможных. Говорят,
что вероятность того, что монетка
упадет орлом, равна 1/2.

11.

Бросим игральную кость. У кубика шесть граней,
поэтому возможных исходов тоже шесть.
Например, вы загадали, что выпадет три очка. Это
один исход из шести возможных. В теории
вероятностей он будет называться благоприятным
исходом.
Вероятность выпадения тройки равна 1/6 (один
благоприятный исход из шести возможных).
Вероятность четверки — тоже 1/6
А вот вероятность появления семерки равна нулю.
Ведь грани с семью точками на кубике нет.
Вероятность события равна отношению
числа благоприятных исходов к общему
числу исходов.
Вероятность не может быть больше единицы.

12.

Вероятностью события А называется
отношение числа m элементарных
исходов, благоприятствующих этому
событию, к общему числу элементарных
исходов испытания n.
m
p P(a)
n

13.

Примеры:
1)Из ящика с разноцветными
шарами наугад вынимают
черный шар.
2)При бросании игральной
кости выпала цифра 7.
3)При телефонном вызове
абонент оказался занят.
4)Вы вытащили черный шар.

14.

Достоверным назовем событие
которое обязательно произойдет при
выполнении определенного количества
условий(4 пример).
Событие которое не происходит при
выполнении определенного количества
условий(2 пример).
Случайные события обозначаются большими
латинскими буквами A, B, C,…

15.

Два события называются
несовместными, если появление
одного из них исключает
появление другого.
В противном случае события
называются совместными.

16.

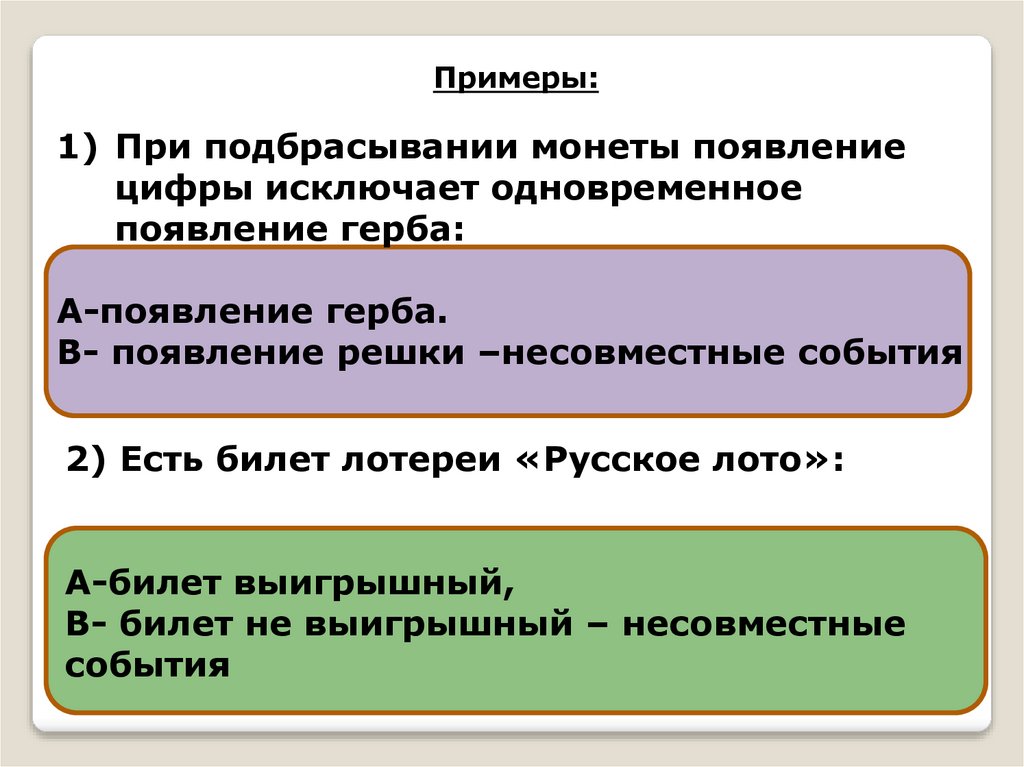
Примеры:
1) При подбрасывании монеты появление
цифры исключает одновременное
появление герба:
А-появление герба.
В- появление решки –несовместные события
2) Есть билет лотереи «Русское лото»:
А-билет выигрышный,
В- билет не выигрышный – несовместные
события

17.

Если возможные исходы (результаты)
опыта являются событиями
несовместными, достоверными, то
каждый из результатов испытания
назовем элементарным исходом.
Те элементарные исходы, при которых
интересующее нас событие наступает,
назовем благоприятствующими этому
событию исходами.

18.

Примеры решения задач
1.В случайном эксперименте бросают две
игральные кости. Найдите вероятность
того, что в сумме выпадет 7 очков.
Результат округлите до сотых
.

19.

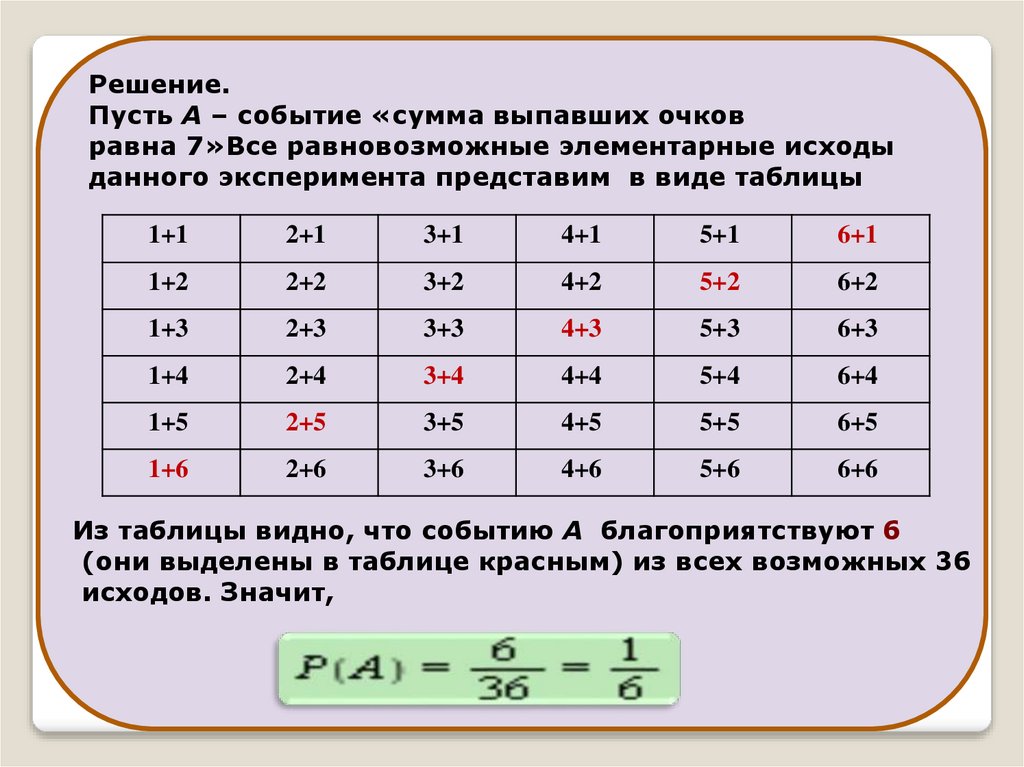
Решение.
Пусть А – событие «сумма выпавших очков
равна 7»Все равновозможные элементарные исходы
данного эксперимента представим в виде таблицы
1+1
2+1
3+1
4+1
5+1
6+1
1+2
2+2
3+2
4+2
5+2
6+2
1+3
2+3
3+3
4+3
5+3
6+3
1+4
2+4
3+4
4+4
5+4
6+4
1+5
2+5
3+5
4+5
5+5
6+5
1+6
2+6
3+6
4+6
5+6
6+6
Из таблицы видно, что событию А благоприятствуют 6
(они выделены в таблице красным) из всех возможных 36
исходов. Значит,

20.

2. В сборнике билетов по биологии
всего 25 билетов, в двух из них
встречается вопрос о грибах. На экзамене
школьнику достаётся один случайно
выбранный билет. Найдите вероятность
того, что в этом билете не будет вопроса
о грибах.
Решение.
Очевидно, вероятность вытащить
билет без вопроса о грибах равна
23/25, то есть 0,92.

21.

3. В чемпионате по гимнастике
участвуют 20 спортсменок: 8 из России,
7 из США, остальные — из Китая.
Порядок, в котором выступают
гимнастки, определяется жребием.
Найдите вероятность того, что
спортсменка, выступающая последней,
окажется из Китая.

22.

Решение.
Давайте представим,
что все спортсменки
одновременно
подошли к шляпе
и вытянули из нее
бумажки с номерами.
Кому-то из них
достанется двадцатый
номер. Вероятность
того, что его вытянет
китайская
спортсменка,
равен 5/20 (поскольку
из Китая —
5 спортсменок).
Ответ: 0,25.

23.

4. Монета брошена 2 раза. Какова вероятность события: Авыпадет одновременно два герба?
Решение:
Сколько всего возможно результатов опыта?
ГГ, ГР, РР, РГ
Таким образом, всего возможно результатов n=4, нас
интересующий результат
возможен только один раз
m=1, поэтому
m
1
P ( A)
.
n
4
Ответ: 0,25

24.

5. В коробке имеется 3 кубика: чёрный, красный и белый.
Вытаскивая кубики наугад, мы ставим их
последовательно друг за другом. Какова вероятность того,
что в результате получится последовательность: красный,
чёрный, белый?
Решение.
Сколько всего возможно результатов опыта?
Пусть Ч – черный кубик, К – красный кубик, Б – белый
кубик, тогда
ЧКБ, ЧБК, БЧК, БКЧ,
КЧБ, КБЧ.
Ответ:
1
6

25.

Домашнее задание:
Выучить теоретический
материал