Похожие презентации:
Постоянный электрический ток. (Лекция 6)
1. Постоянный электрический ток
Лекция 6CEE
2. План
Электрический ток и его характеристики.Электродвижущая сила источника тока.
Напряжение.
Закон Ома для однородного участка цепи.
Закон Ома в дифференциальной форме.
Закон Ома для неоднородного участка
цепи.
CEE
3. Электрический ток и его характеристики
CEE4.
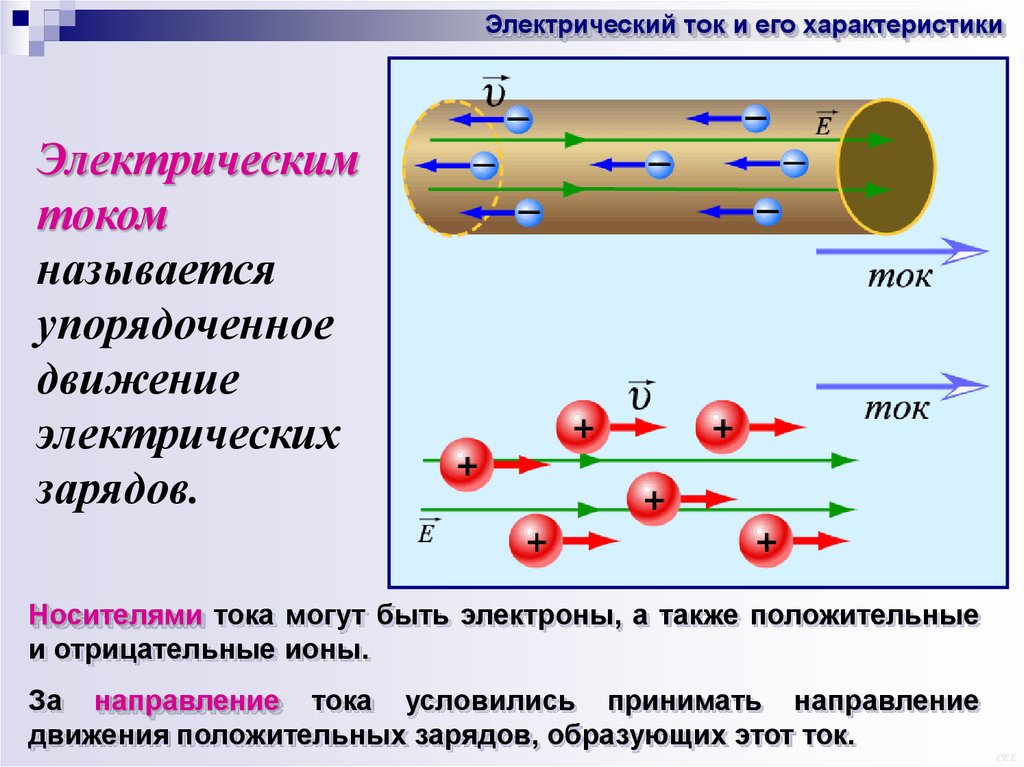
Электрический ток и его характеристикиЭлектрическим
током
называется
упорядоченное
движение
электрических
зарядов.
Носителями тока могут быть электроны, а также положительные
и отрицательные ионы.
За направление тока условились принимать направление
движения положительных зарядов, образующих этот ток.
CEE
5.
Электрический ток и его характеристикиЕсли за время dt через поперечное сечение
проводника переносится заряд dq, то сила
тока
dq
i
dt
(1)
Ток, не изменяющийся со временем, называется постоянным.
Для постоянного тока
q
I
t
(2)
CEE
6.
Электрический ток и его характеристикиq
I
t
Единицей силы тока в СИ
является А − ампер.
Кл
i A
c
Ампер (Ampere) Андре-Мари (22.I.1775–10.VI.1836)
CEE
7.
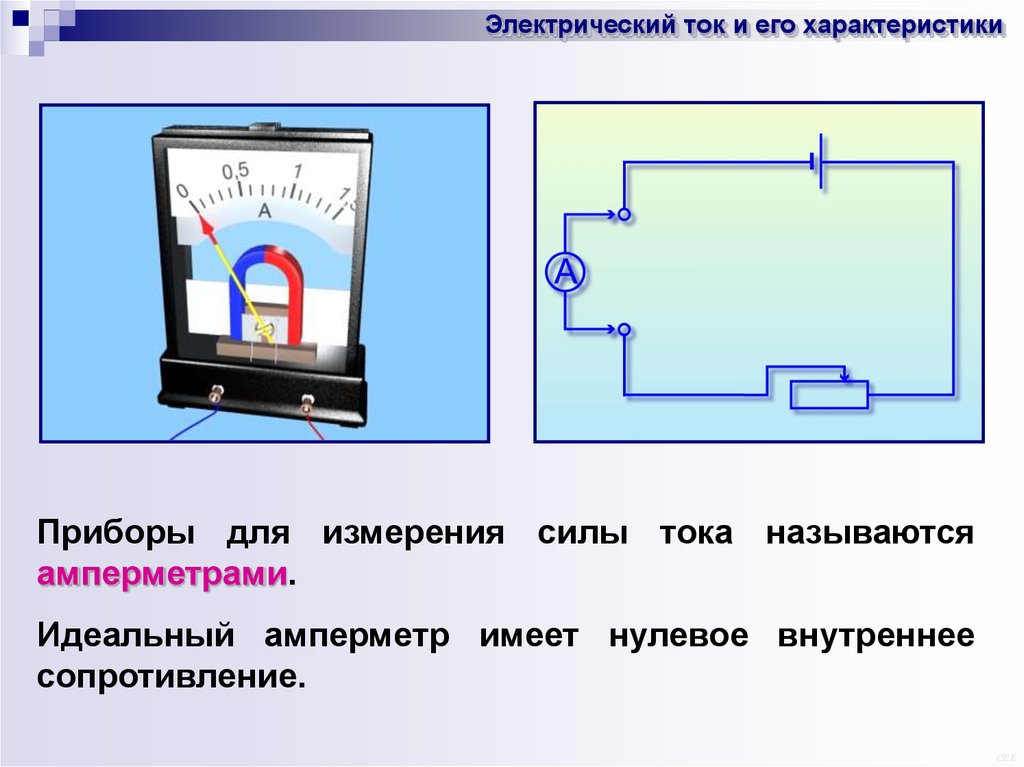
Электрический ток и его характеристикиПриборы для измерения силы тока называются
амперметрами.
Идеальный амперметр имеет нулевое внутреннее
сопротивление.
CEE
8.
Электрический ток и его характеристикиЕсли ток в проводнике создается как положительными, так и
отрицательными носителями зарядов одновременно, то
dq
dq
I
dt
dt
(3)
Электрический ток может быть неравномерно распределен по
поверхности, через которую он течет.
Более
детально
электрический
ток
можно
характеризовать с помощью вектора плотности
тока. Он численно равен отношению силы тока dI
через
расположенную
перпендикулярно
направлению тока площадку dS┴ к величине этой
площадки, т. е.
A
j 2
м
dI
j
dS
(4)
По направлению вектор плотности тока совпадает
с
направлением
скорости
упорядоченного
движения положительных зарядов.
CEE
9.
Электрический ток и его характеристикиdS
n
Зная j в каждой точке сечения
проводника, можно найти силу тока I
через любую поверхность S :
j
I j dS jn dS
S
где
(5)
S
dS dSn; j dS jdS cos jn dS ,
jn
проекция
j наn
CEE
10. Электродвижущая сила источника тока. Напряжение
CEE11.
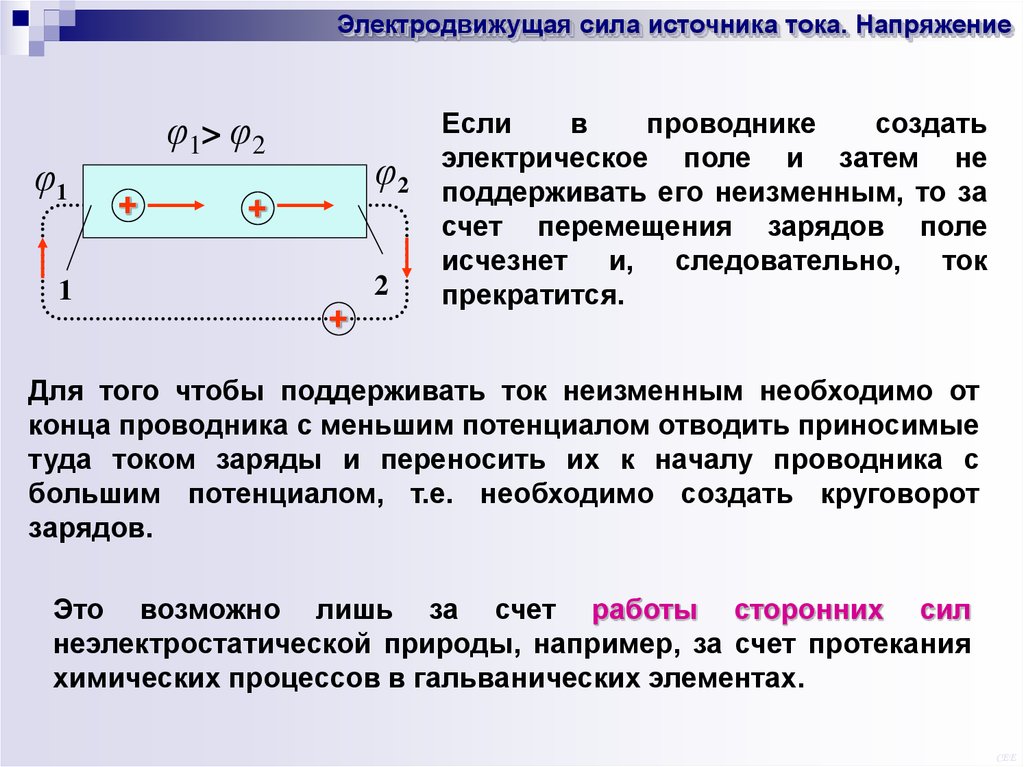
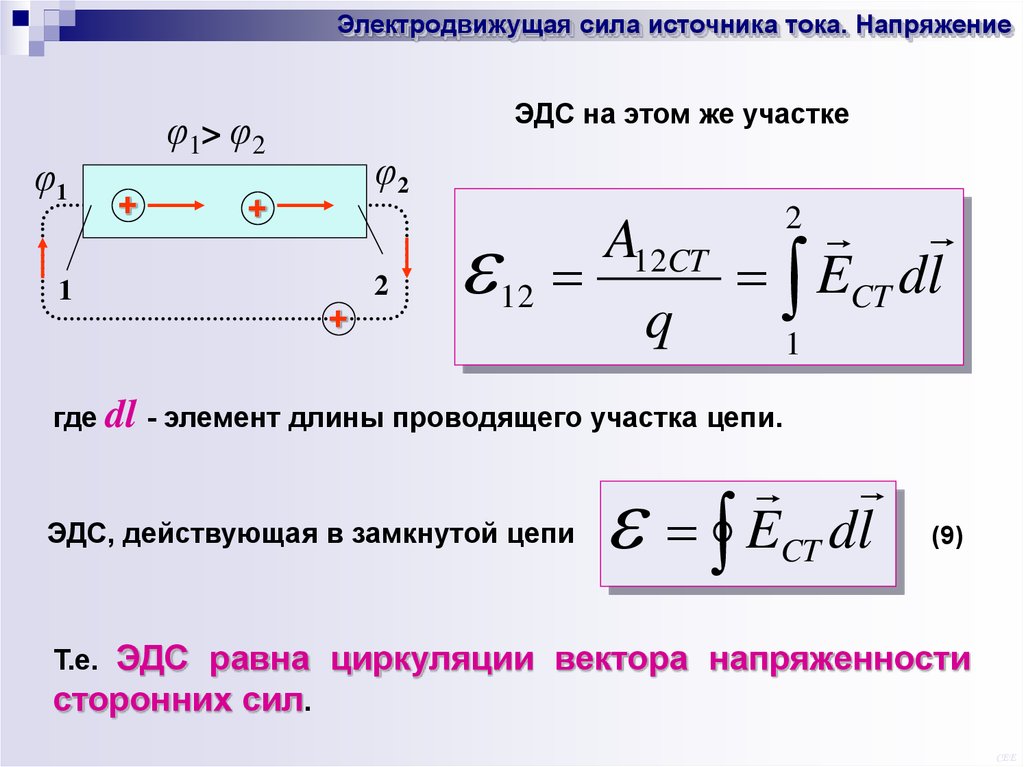
Электродвижущая сила источника тока. Напряжениеφ1
φ1> φ2
+
φ2
+
2
1
+
Если
в
проводнике
создать
электрическое поле и затем не
поддерживать его неизменным, то за
счет перемещения зарядов поле
исчезнет и, следовательно, ток
прекратится.
Для того чтобы поддерживать ток неизменным необходимо от
конца проводника с меньшим потенциалом отводить приносимые
туда током заряды и переносить их к началу проводника с
большим потенциалом, т.е. необходимо создать круговорот
зарядов.
Это возможно лишь за счет работы сторонних сил
неэлектростатической природы, например, за счет протекания
химических процессов в гальванических элементах.
CEE
12.
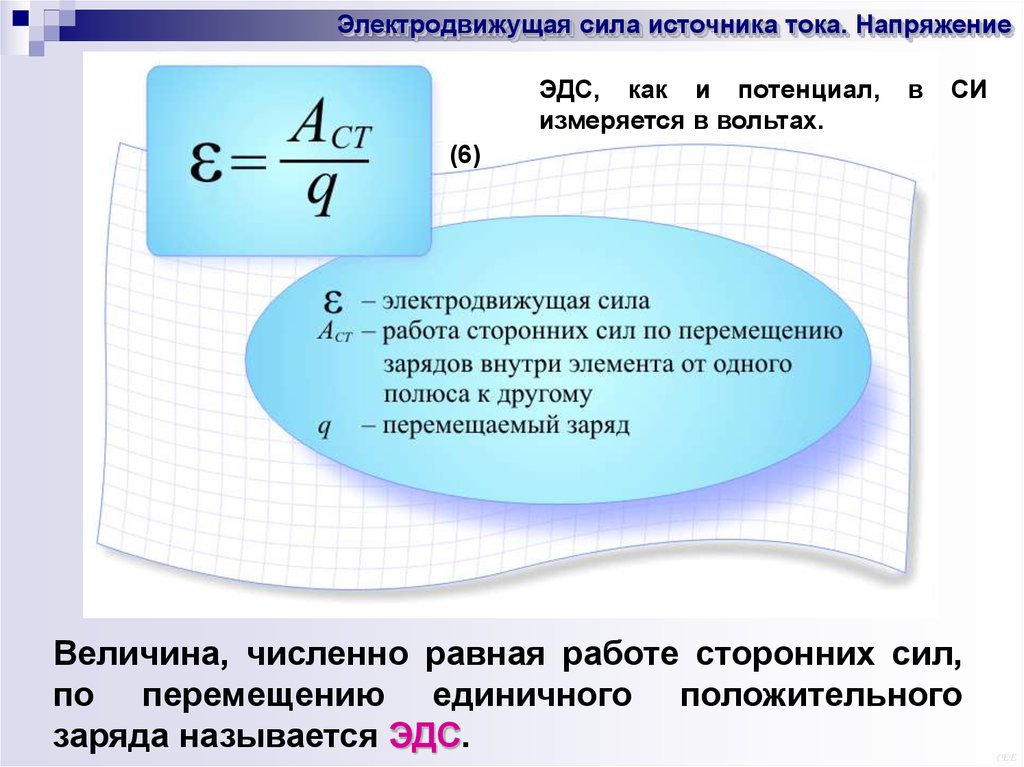
Электродвижущая сила источника тока. НапряжениеЭДС, как и потенциал,
измеряется в вольтах.
в
СИ
(6)
Величина, численно равная работе сторонних сил,
по перемещению единичного положительного
заряда называется ЭДС.
CEE
13.
Электродвижущая сила источника тока. Напряжениеφ1
Представим стороннюю силу как
φ1> φ2
+
φ2
+
2
1
FCT qECT
(7)
+
Тогда работа сторонних сил на участке 1-2 цепи будет равна
2
FCT dl q ECT dl
2
A12CT
1
(8)
1
CEE
14.
Электродвижущая сила источника тока. Напряжениеφ1
ЭДС на этом же участке
φ1> φ2
+
φ2
+
2
1
+
A12CT
ECT dl
q
1
2
12
где dl - элемент длины проводящего участка цепи.
ЭДС, действующая в замкнутой цепи
ECT dl
(9)
Т.е. ЭДС равна циркуляции вектора напряженности
сторонних сил.
CEE
15.
Электродвижущая сила источника тока. Напряжениеφ1
φ1> φ2
+
φ2
+
2
1
+
Работа, совершаемая этой
силой над зарядом q на
участке 1-2 цепи,
Однако, кроме сторонних сил, на
носители тока действуют силы
электростатического поля qE.
Следовательно,
результирующая
сила, действующая в каждой точке
цепи на заряд
F q( E ECT )
(10)
2
A12 Fdl q ( E ECT )dl q( 1 2 ) q 12
2
1
1
(11)
CEE
16.
Электродвижущая сила источника тока. Напряжениеφ1
φ1> φ2
+
φ2
+
2
1
+
Величина, численно равная работе,
совершаемой
электрическими
и
сторонними силами над единичным
положительным зарядом, называется падением напряжения или
просто напряжением U на данном
участке, т. е.
A12
U12
1 2 12 .
q
Участок цепи, на котором не
действуют
сторонние
силы,
называется однородным. Для него
Участок цепи, на котором
называется неоднородным.
(12)
U12 1 2
действуют
сторонние
(13)
силы,
Для замкнутой цепи ( 1 2) = 0 и поэтому U = ε.
CEE
17. Закон Ома для однородного участка цепи (не содержащего источника тока)
CEE18.
Закон Ома для однородного участка цепи (несодержащего источника тока)
Ом в 1826 г. экспериментально установил
закон, который называется законом Ома
для однородного участка цепи:
(14)
B
R 1 1Ом
A
СИЛА ТОКА, ТЕКУЩЕГО ПО ОДНОРОДНОМУ МЕТАЛЛИЧЕСКОМУ
ПРОВОДНИКУ, ПРЯМО ПРОПОРЦИОНАЛЬНА ПАДЕНИЮ НАПРЯЖЕНИЯ
НА ПРОВОДНИКЕ И ОБРАТНО ПРОПОРЦИОНАЛЬНА СОПРОТИВЛЕНИЮ
ПРОВОДНИКА.
CEE
19.
CEE20.
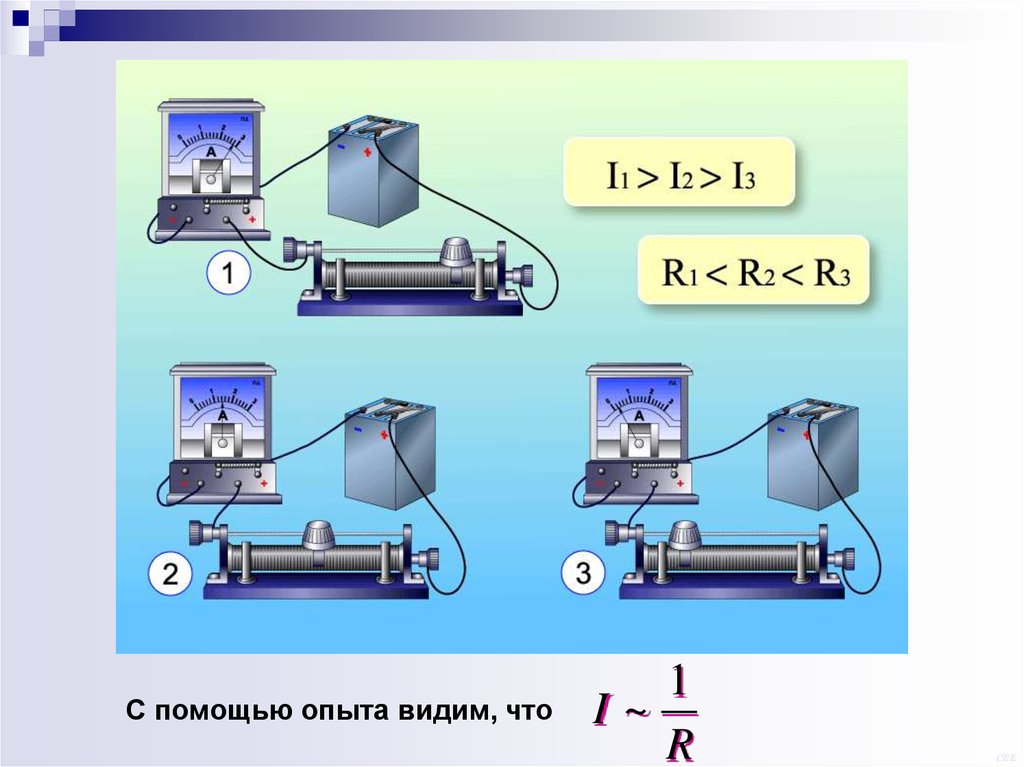
С помощью опыта видим, что1
I~
R
CEE
21.
Сопротивление проводника(15)
1Ом м
CEE
22.
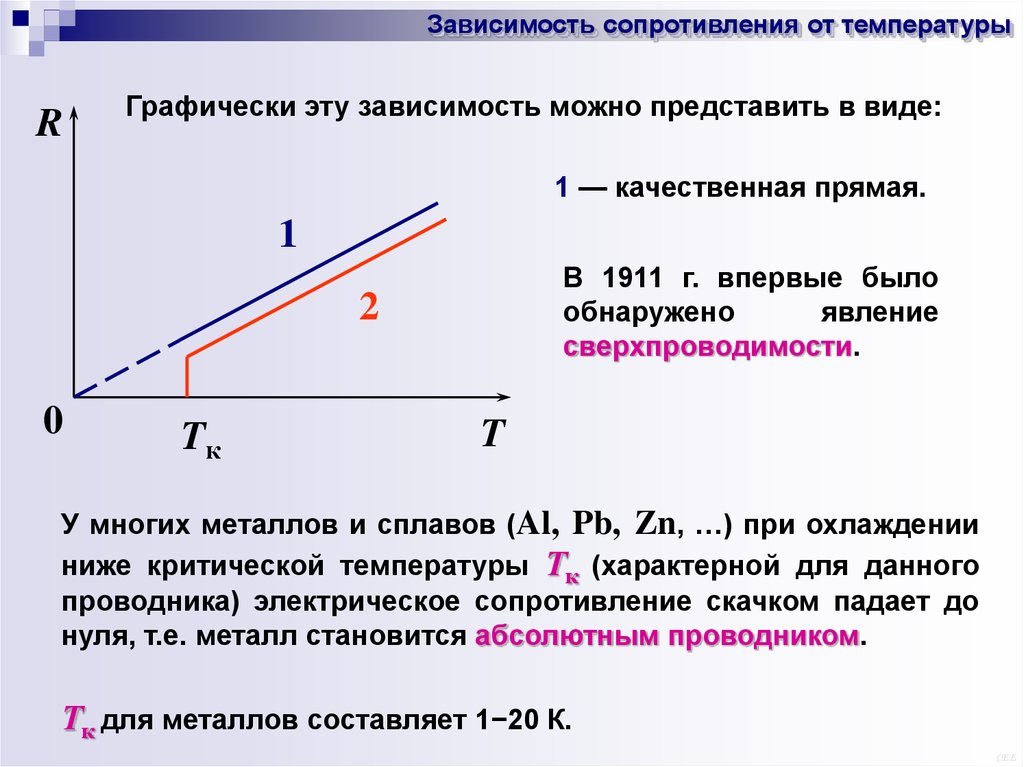
Зависимость сопротивления от температурыС
ростом
температуры
сопротивление
металлических проводников увеличивается.
R R0 T
R R0 (1 t )
0 T
0 (1 t )
(16)
(17)
ρ0 — удельное сопротивление при температуре t = 0°C;
— температурный коэффициент сопротивления, для
большинства металлов близкий к 1/273 К-1 при не очень низких
температурах;
T — термодинамическая температура.
CEE
23.
Зависимость сопротивления от температурыR
Графически эту зависимость можно представить в виде:
1 — качественная прямая.
1
В 1911 г. впервые было
обнаружено
явление
сверхпроводимости.
2
0
Tк
T
У многих металлов и сплавов (Al, Pb, Zn, …) при охлаждении
ниже критической температуры Тк (характерной для данного
проводника) электрическое сопротивление скачком падает до
нуля, т.е. металл становится абсолютным проводником.
Тк для металлов составляет 1−20 К.
CEE
24. Закон Ома для однородного участка цепи в дифференциальной форме
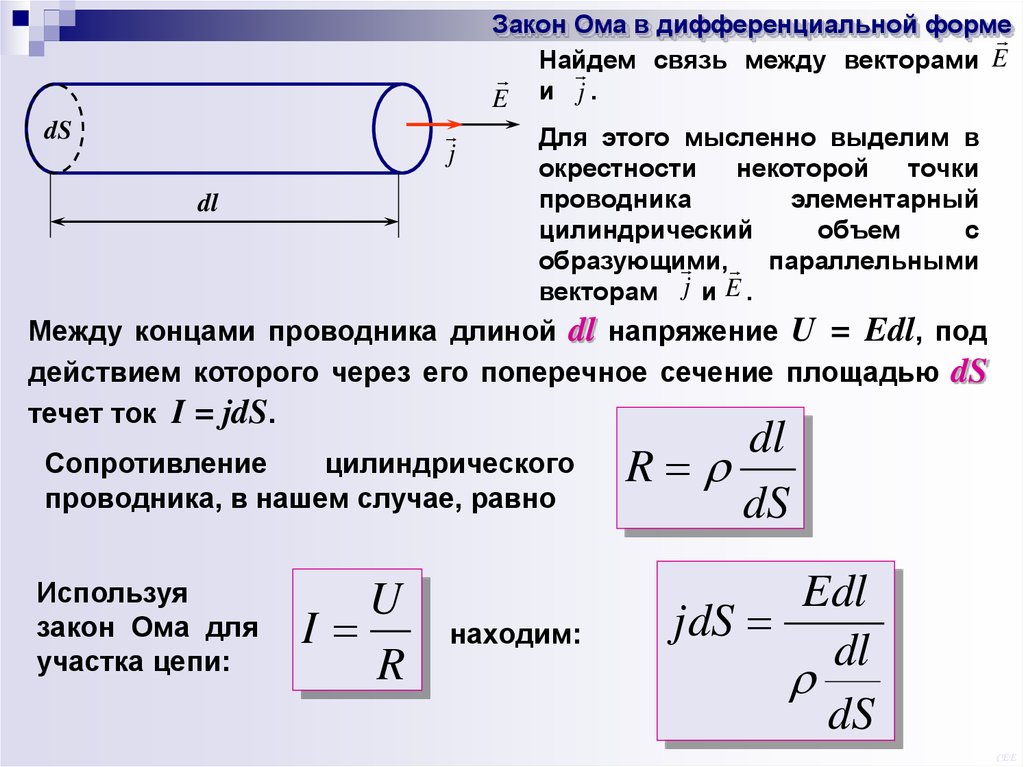
CEE25.
Закон Ома в дифференциальной формеНайдем
связь между векторами E
E и j.
j
dS
dl
Для этого мысленно выделим в
окрестности
некоторой
точки
проводника
элементарный
цилиндрический
объем
с
образующими,
параллельными
векторам j и E .
Между концами проводника длиной dl напряжение U = Edl, под
действием которого через его поперечное сечение площадью dS
течет ток I = jdS.
Сопротивление
цилиндрического
проводника, в нашем случае, равно
Используя
закон Ома для
участка цепи:
U
I
R
находим:
dl
R
dS
Edl
jdS
dl
dS
CEE
26.
Закон Ома в дифференциальной формеEdl
jdS
dl
dS
=>
1
j E γE
(18)
Закон Ома для
однородного участка
цепи в
дифференциальной
форме
γ
1
— удельная электрическая проводимость.
1 / (Ом · м) = 1 См / м, где 1 См = 1 / Ом - это единица
измерения электропроводности в СИ, называемая
сименс (См).
CEE
27. Закон Ома для неоднородного участка цепи
CEE28.
Закон Ома для неоднородного участка цепиНа
неоднородном
участке
цепи
плотность
тока
пропорциональна сумме напряженностей электростатического
поля и поля сторонних сил, т.е.
j γ( E ECT )
(19)
Рассмотрим цилиндрический проводник длиной
поперечного сечения
dl
перемещение
S.
l
с площадью
Умножим обе части равенства (19) на
вдоль оси проводника и проинтегрируем
получившееся соотношение по длине проводника от 0 до l:
l
l
j dl γ( Edl ECT dl ),
l
0
0
откуда
0
j l γ( 1 2 ε12 )
(20)
CEE
29.
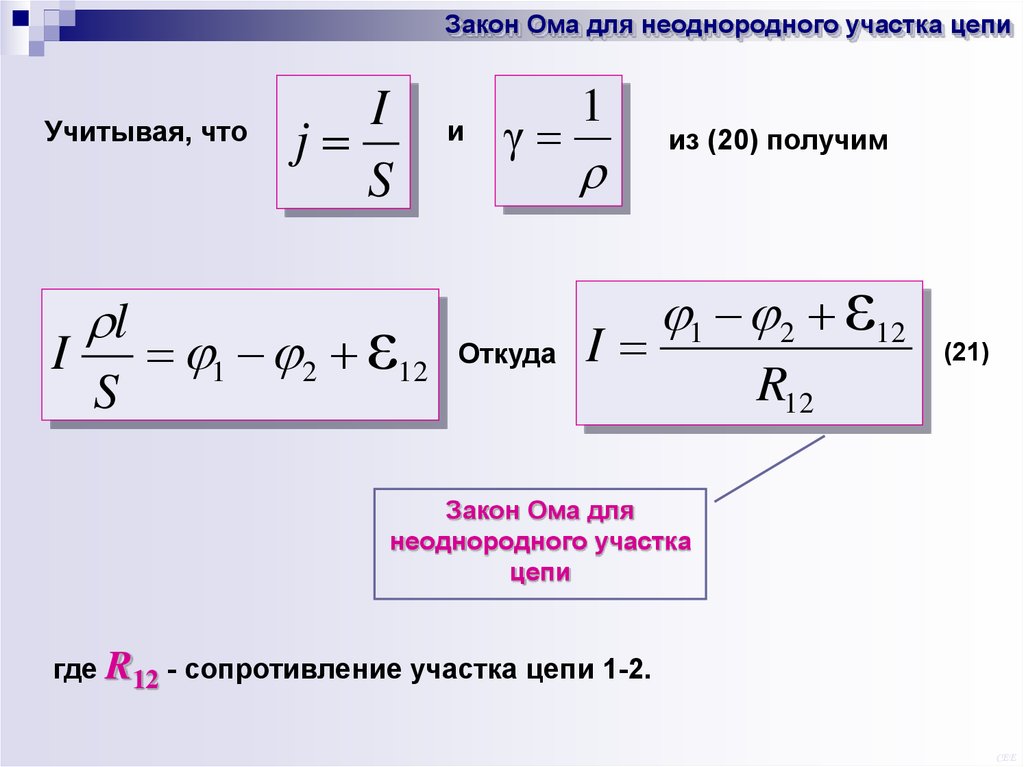
Закон Ома для неоднородного участка цепиУчитывая, что
I
l
S
I
j
S
1 2 ε12
и
γ
Откуда
1
I
из (20) получим
1 2 ε12
(21)
R12
Закон Ома для
неоднородного участка
цепи
где R12 - сопротивление участка цепи 1-2.
CEE
30.
Закон Ома для замкнутой цепиДля замкнутой цепи ( 1
и
поэтому
формула
запишется в виде:
2) = 0
(21)
I
RΣ — суммарное сопротивление всей цепи; ε
I
ε
(22)
R
— ЭДС источника.
Пусть замкнутая цепь состоит из источника
электрической энергии с ЭДС и внутренним
сопротивлением r, а также внешней цепи
потребителя, имеющей сопротивление R.
Согласно (22)
I
ε
R r
(23)
CEE
31.
Закон Ома для замкнутой цепиI
Разность потенциалов на электродах
источника равна напряжению на внешнем
участке цепи:
U = φ1- φ2 = IR = ε
- Ir
(24)
Если цепь разомкнуть, то ток в ней прекратится и напряжение
на зажимах источника станет равным его ЭДС, т.е. U = ε.
Таким образом, напряжение на внешнем участке цепи будет
равно
U = IR = ε R / (R + r)
(25)
CEE
32.
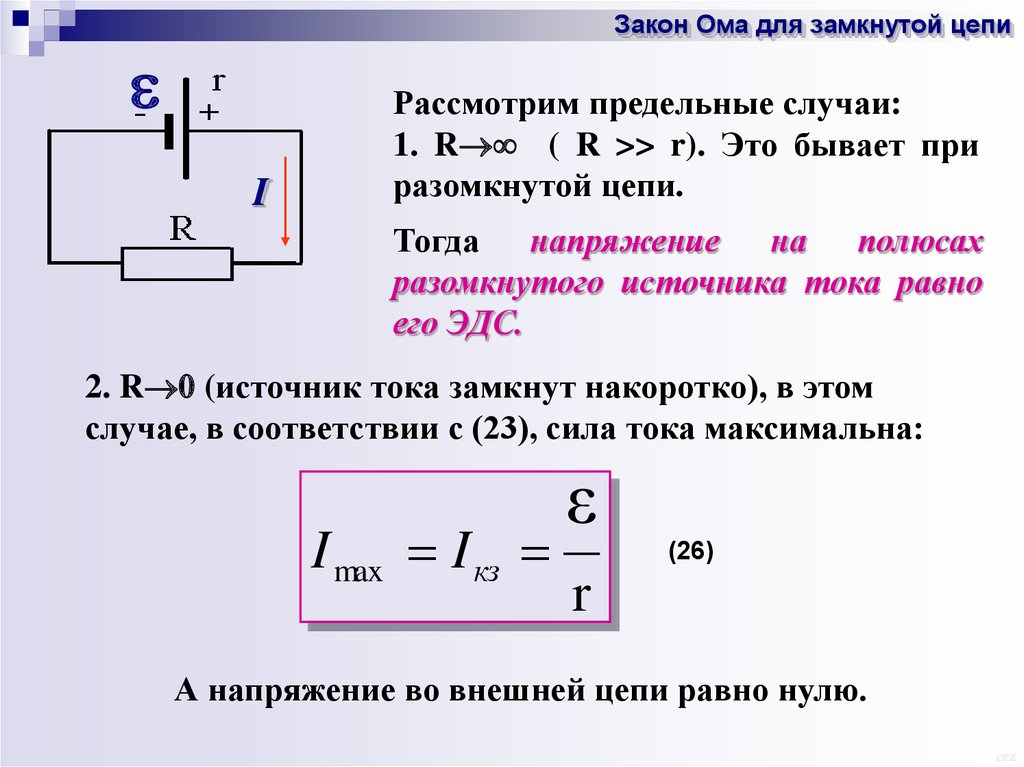
Закон Ома для замкнутой цепиI
Рассмотрим предельные случаи:
1. R ( R >> r). Это бывает при
разомкнутой цепи.
Тогда напряжение на полюсах
разомкнутого источника тока равно
его ЭДС.
2. R (источник тока замкнут накоротко), в этом
случае, в соответствии с (23), сила тока максимальна:
I max I кз
ε
(26)
r
А напряжение во внешней цепи равно нулю.
CEE
33.
Лекцию подготовила к.п.н.доцент Симдянкина Е.Е.
CEE





















 Физика
Физика








