Кинематика

1.

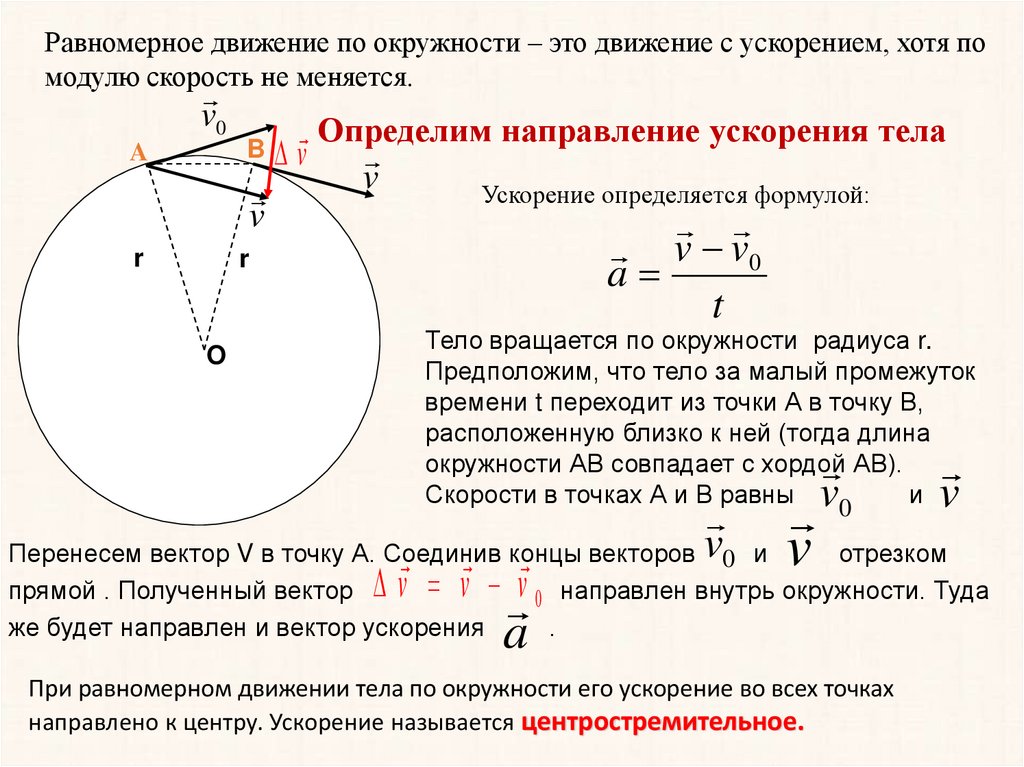
Равномерное движение по окружности – это движение с ускорением, хотя по
модулю скорость не меняется.
v0
Определим направление ускорения тела
v
Ускорение определяется формулой:
v
A
B v
r
r
O
v v0
a
t
Тело вращается по окружности радиуса r.
Предположим, что тело за малый промежуток
времени t переходит из точки А в точку В,
расположенную близко к ней (тогда длина
окружности АВ совпадает с хордой АВ).
Скорости в точках А и В равны
и
0
v
v
Перенесем вектор V в точку А. Соединив
концы
векторов v0 и v отрезком
прямой . Полученный вектор v v v 0 направлен внутрь окружности. Туда
же будет направлен и вектор ускорения
a .
При равномерном движении тела по окружности его ускорение во всех точках
направлено к центру. Ускорение называется центростремительное.

2.

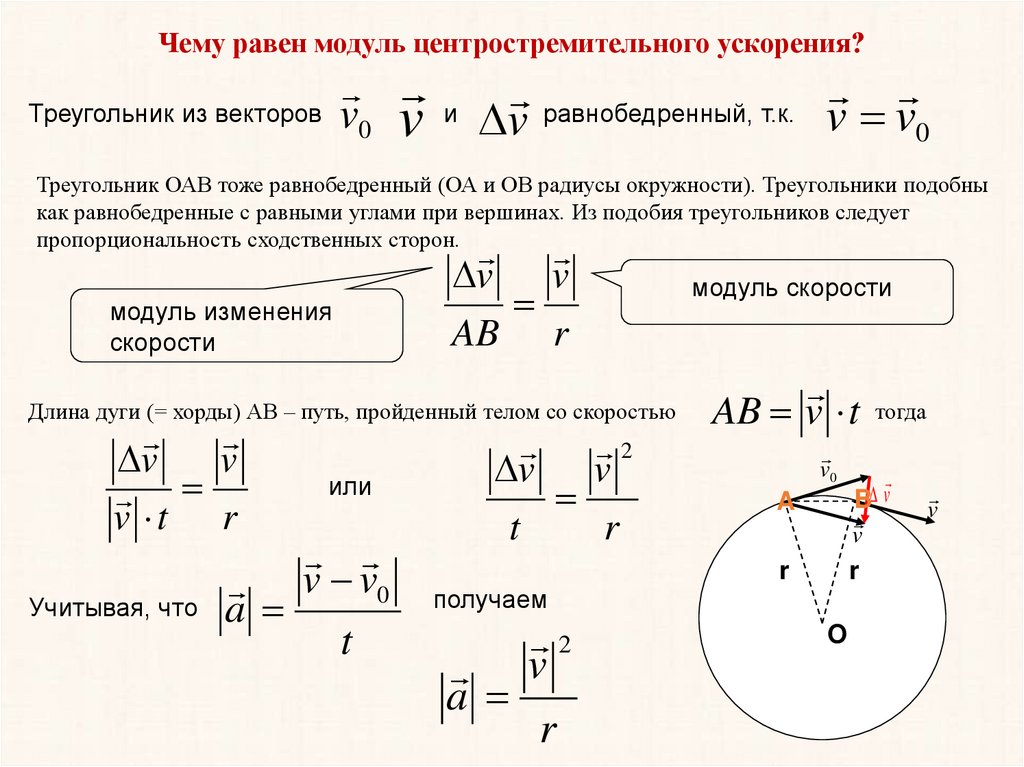
Чему равен модуль центростремительного ускорения?
Треугольник из векторов v
и v равнобедренный, т.к. v v
0 v
0
Треугольник ОАВ тоже равнобедренный (ОА и ОВ радиусы окружности). Треугольники подобны
как равнобедренные с равными углами при вершинах. Из подобия треугольников следует
пропорциональность сходственных сторон.
v
модуль изменения
скорости
v
AB
модуль скорости
r
Длина дуги (= хорды) АВ – путь, пройденный телом со скоростью
v
v
v t r
Учитывая, что a
или
v v0
t
v
t
2
v
r
AB v t тогда
v0
A
v
B
v
r
r
получаем
a
2
v
r
O
v

3.

ΔS
Δφ
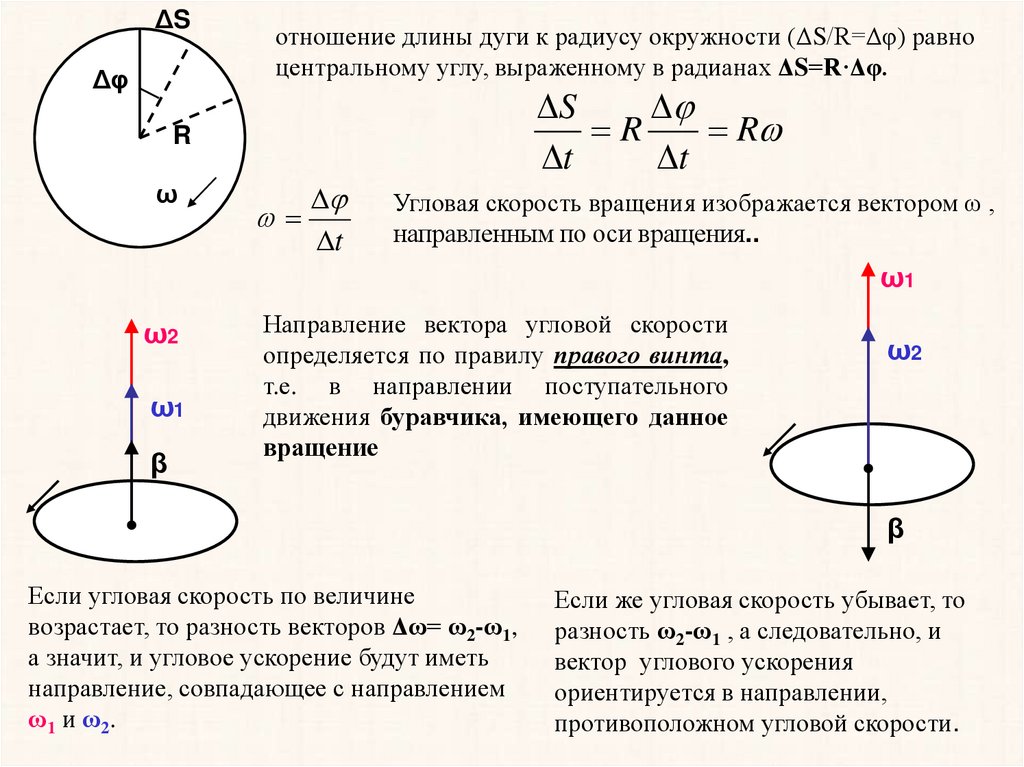
отношение длины дуги к радиусу окружности (ΔS/R=Δφ) равно
центральному углу, выраженному в радианах ΔS=R·Δφ.
S
R
R
t
t
R
ω
t
Угловая скорость вращения изображается вектором ω ,
направленным по оси вращения..
ω1
ω2
ω1
β
Направление вектора угловой скорости
определяется по правилу правого винта,
т.е. в направлении поступательного
движения буравчика, имеющего данное
вращение
ω2
β
Если угловая скорость по величине
возрастает, то разность векторов Δω= ω2-ω1,
а значит, и угловое ускорение будут иметь
направление, совпадающее с направлением
ω1 и ω2.
Если же угловая скорость убывает, то
разность ω2-ω1 , а следовательно, и
вектор углового ускорения
ориентируется в направлении,
противоположном угловой скорости.

4.

Уменьшая промежуток времени Δt, можно найти предел отношения
lim
t 0 t
Угловая скорость вращения в данный
момент времени. Размерность рад/с или с-1
ω2
Изменение вектора угловой скорости со временем характеризуется
угловым ускорением
d
lim
t 0 t
dt
ω1
β
Размерность рад/с2 или с-2
Угловое ускорение тоже векторная величина. Если угловая
скорость по величине возрастает, то разность векторов
Δω= ω2-ω1,
а следовательно, и угловое ускорение будут иметь
направление, совпадающее с направлением ω1 и ω2.
Если же угловая скорость убывает, то разность векторов
Δω= ω2-ω1 , а следовательно, и вектор углового ускорения
ориентируется в направлении, противоположном угловой
скорости.
ω1
ω2
β

5.

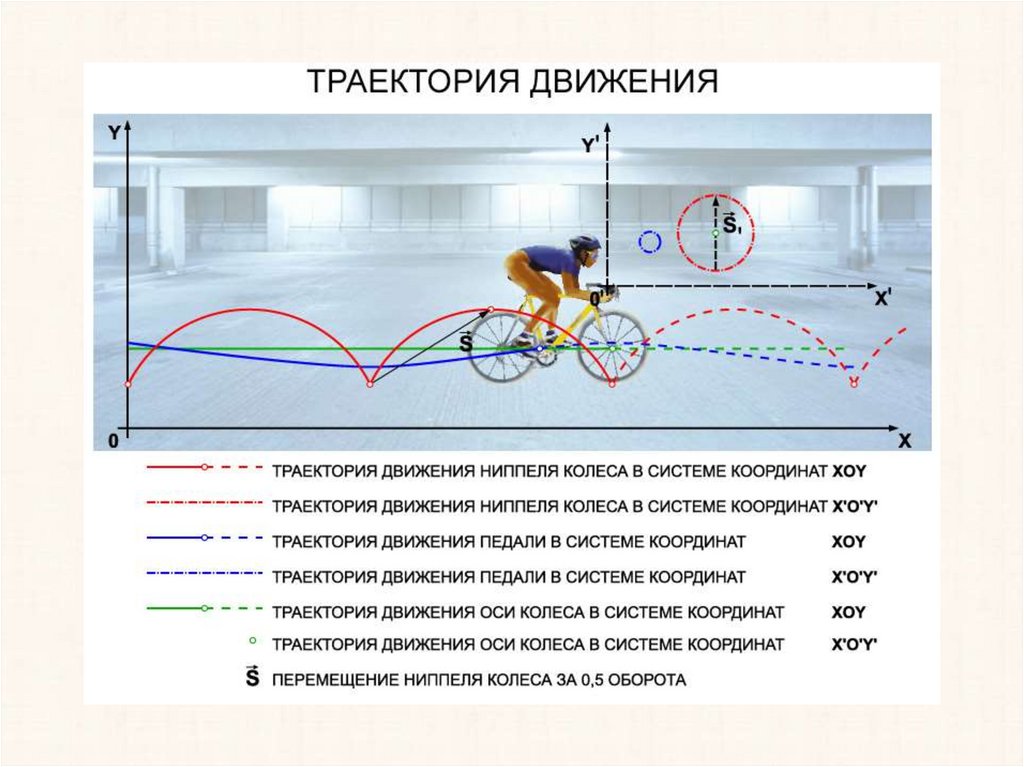
Период обращения
Движение тела по окружности часто характеризуют не скоростью v , а
промежутком времени, за который тело совершает один полный оборот.
Эта величина называется периодом обращения Т.
Единица измерения – 1с (секунда)
Если известен период обращения Т, то легко найти и скорость v
движения тела по окружности.
За время, равное периоду Т, тело проходит путь, равный длине окружности
2πr. Тогда
2 r
v
T
радиус окружности
Подставив это выражение в формулу ускорения, получаем еще одно
выражение для центростремительного ускорения
4 r
a 2
T
2

6.

Частота обращения
Движение точки по окружности можно характеризовать числом
оборотов по окружности в единицу времени
Эта величина называется частота обращения n
С периодом обращения она связана обратной зависимостью.
1
n
T
Единица измерения
1/с , или с-1
Скорость движения тела по окружности можно выразить и через
частоту n. При одном обороте тело проходит путь 2πr. Тогда при n
оборотах тело за 1с пройдет путь 2πrn.
v 2 r n
Подставим это выражение в формулу для ускорения
a 4 n r
2
2

7.

В зависимости от тангенциальных и нормальных
составляющих ускорения виды движений делятся на :
1) an =0; at = 0
– прямолинейное равномерное движение
2) an =0; at =±const – прямолинейное равноускоренное (+) или
равнозамедленное (-) движение
3) an =0; at = f(t)
– прямолинейное движение с переменным
ускорением
4) an = f(t); at = 0
– равномерное криволинейное движение.
Если an = const, то движение происходит
по окружности.
5) an ≠ 0; at ≠ 0
– криволинейное движение с переменным (at
= f(t)) или постоянным (at =±const)
ускорением.

8.

Поступательное движение
Вращательное движение
Равномерное
S=υ·t
φ=ω·t
υ=const
ω=const
a=0
β=0
Равнопеременное
S=υ0·t+at2/2
φ= ω0+ βt2/2
υ= υ0+ at
ω= ω0+ βt
a=const
β= const
Неравномерное
S=f(t)
φ=f(t)
υ=dS/dt
ω=dφ/dt
a= dυ/dt= d2S/dt2
β=dω/dt= d2φ/dt2

9.

10. Относительность движения

р
л
л р
л
S Sл S р
р
л р
л р
S Sл S р
S Sл S р
2
2
2
2

11.

12.

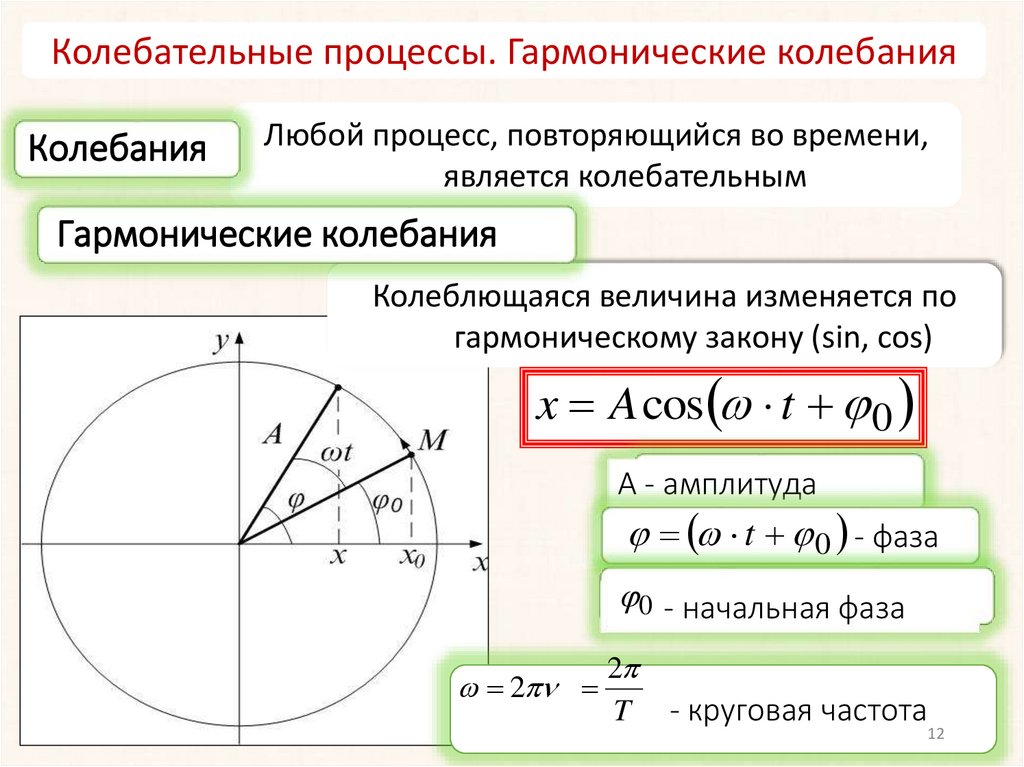
Колебательные процессы. Гармонические колебания
Колебания
Любой процесс, повторяющийся во времени,
является колебательным
Гармонические колебания
Колеблющаяся величина изменяется по
гармоническому закону (sin, cos)
x A cos t 0
А - амплитуда
t 0 - фаза
0 - начальная фаза
2
2
T
- круговая частота
12

13.

Представление гармонических
колебаний:
x A cos t 0
1) по методу векторных диаграмм :
2) как комплексное число:
S Ae
i t 0
По формуле Эйлера:
S Aei t 0 A cos t 0 i sin t 0
x Re S A cos t 0 y Im S A sin t 0
13

14.

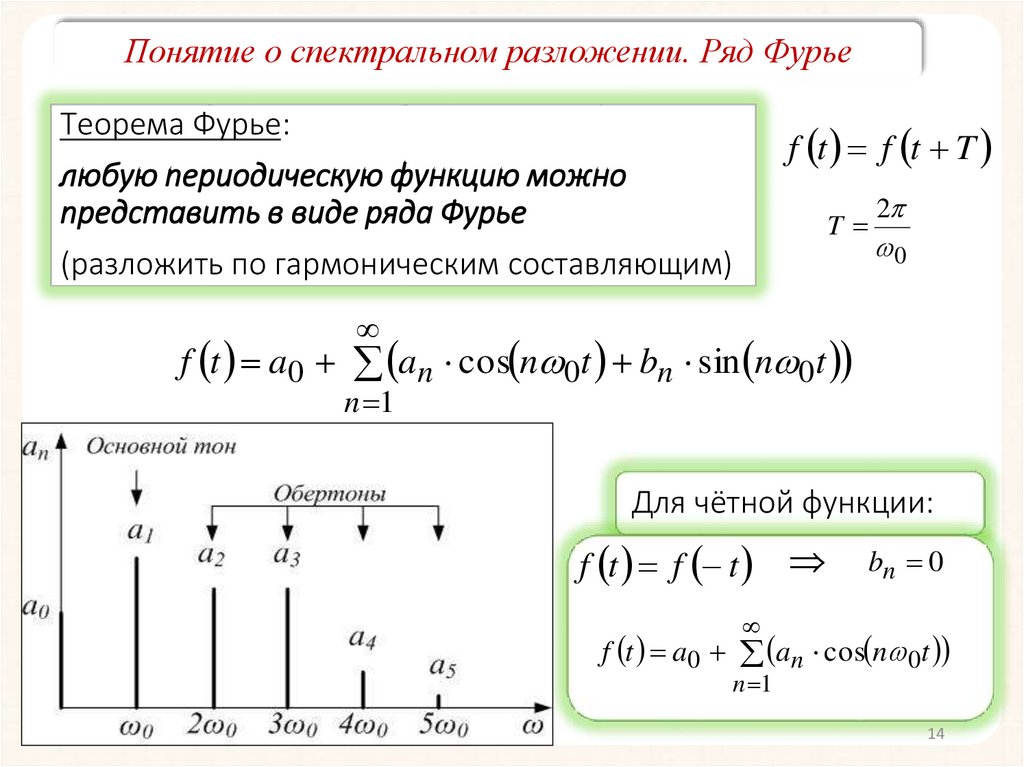
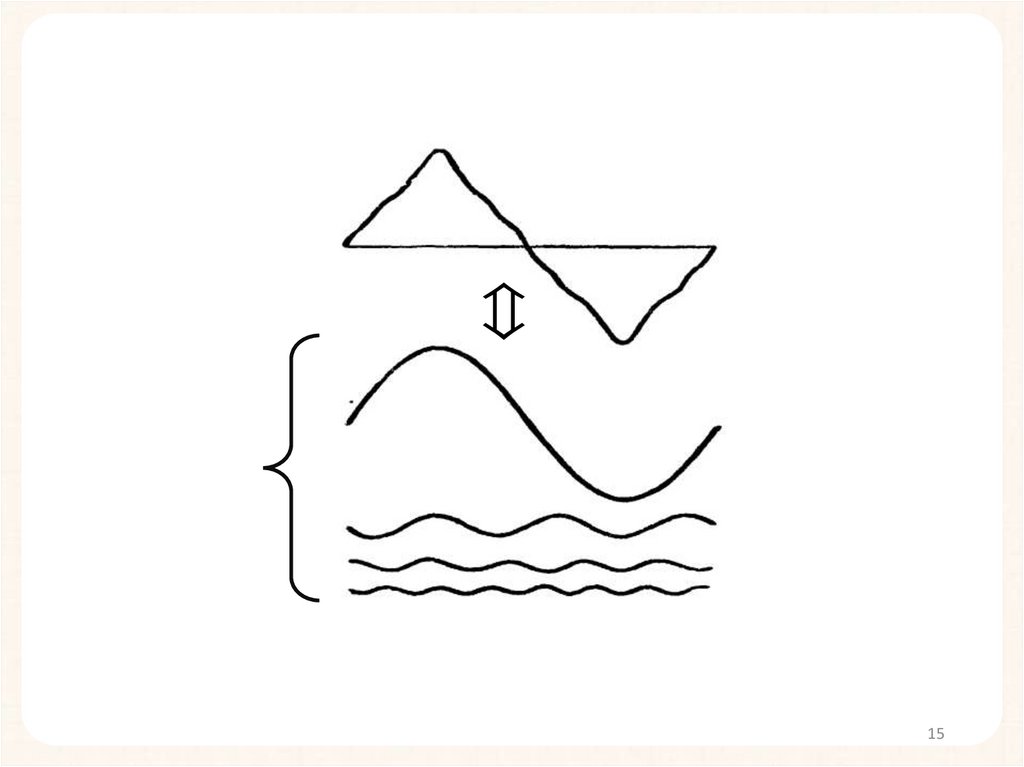
Понятие о спектральном разложении. Ряд Фурье
Теорема Фурье:
любую периодическую функцию можно
представить в виде ряда Фурье
(разложить по гармоническим составляющим)
f t f t T
T
2
0
f t a0 an cos n 0t bn sin n 0t
n 1
Для чётной функции:
f t f t
bn 0
f t a0 an cos n 0t
n 1
14

15.

15

16.

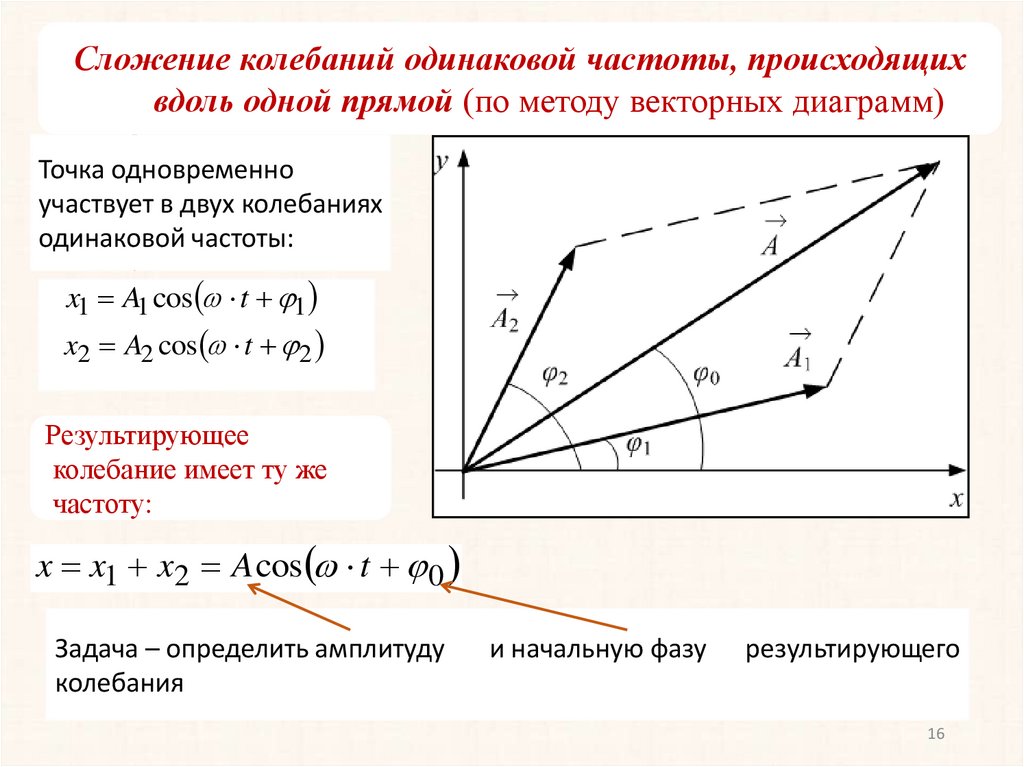
Сложение колебаний одинаковой частоты, происходящих
вдоль одной прямой (по методу векторных диаграмм)
Точка одновременно
участвует в двух колебаниях
одинаковой частоты:
x1 A1 cos t 1
x2 A2 cos t 2
Результирующее
колебание имеет ту же
частоту:
x x1 x2 A cos t 0
Задача – определить амплитуду
колебания
и начальную фазу
результирующего
16

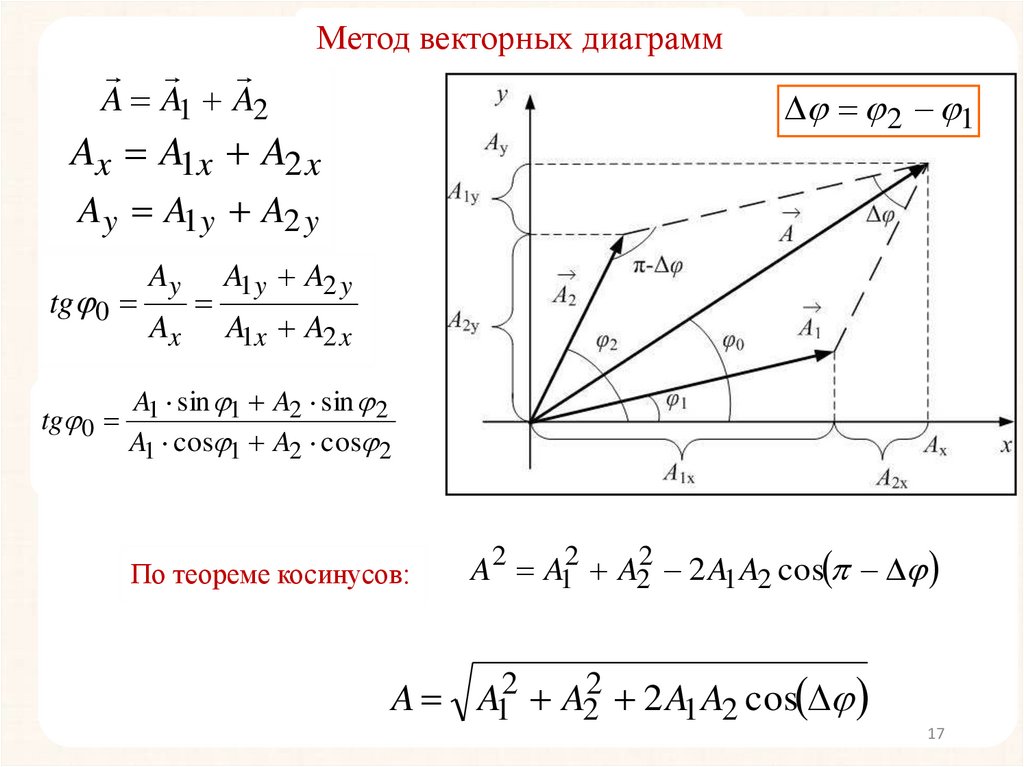
17.

A A1 A2
Метод векторных диаграмм
2 1
Ax A1x A2 x
Ay A1 y A2 y
tg 0
Ay
Ax
A1 y A2 y
A1x A2 x
A sin 1 A2 sin 2
tg 0 1
A1 cos 1 A2 cos 2
По теореме косинусов:
A2 A12 A22 2 A1 A2 cos
A A12 A22 2 A1 A2 cos
17

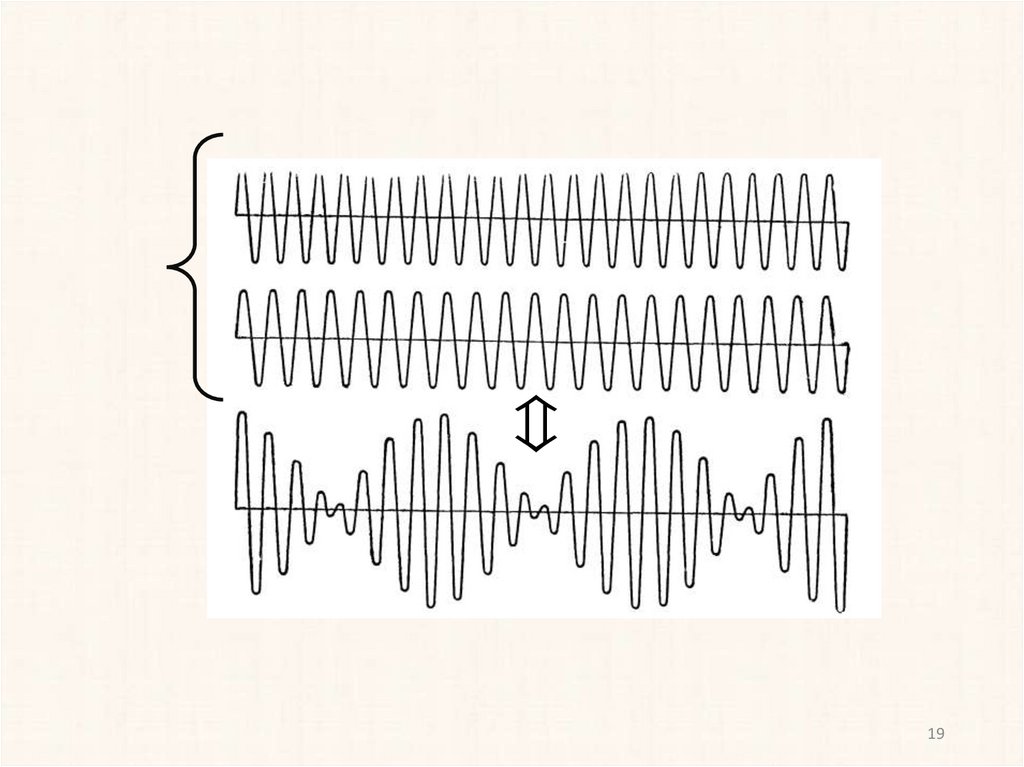
18.

Биения
Если амплитуды двух гармонических колебаний, направленных вдоль
одной прямой, одинаковы А1 = А2 = А, а их частоты мало отличаются
друг от друга Δω = ω2 – ω1 << ω1, то результирующее сложение этих
колебаний получается с периодически изменяющейся амплитудой Аб.
Периодические изменения амплитуды от минимального значения до
максимального называются биениями.
x1 Acos t ,
Уравнения колебаний имеют
x2 Acos( )t.
вид :
Уравнение результирующего колебания:

19.

19

20.

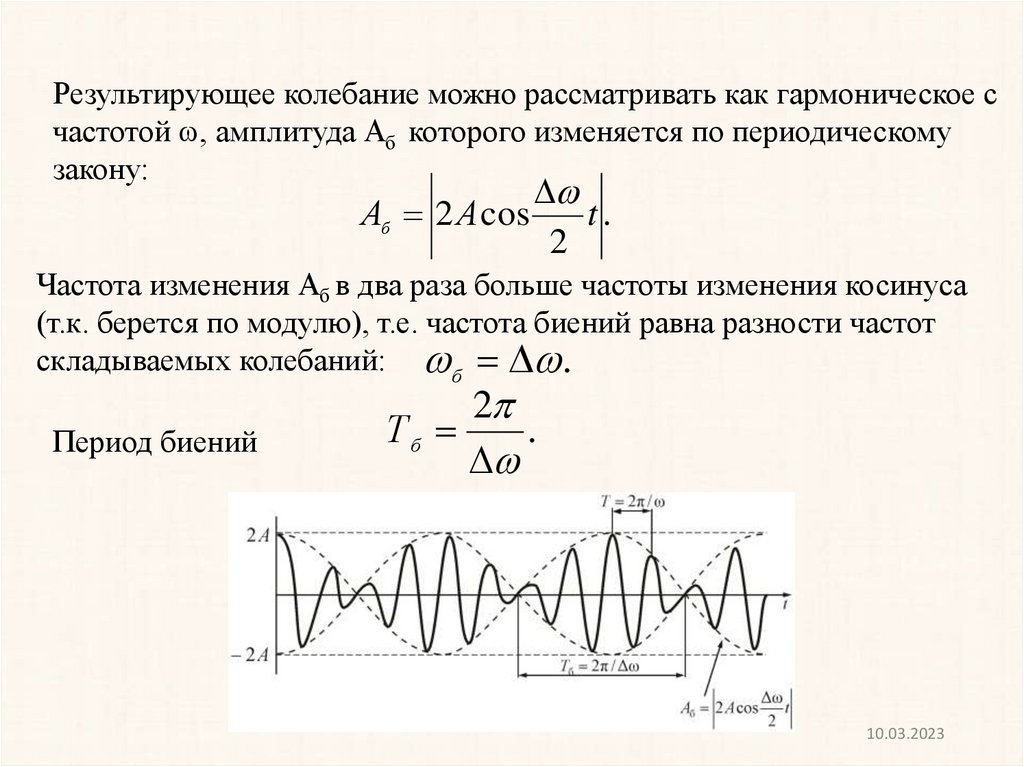
Результирующее колебание можно рассматривать как гармоническое с
частотой , амплитуда Аб которого изменяется по периодическому
закону:
Аб 2 А cos
t.
2
Частота изменения Аб в два раза больше частоты изменения косинуса
(т.к. берется по модулю), т.е. частота биений равна разности частот
складываемых колебаний: б .
Период биений
2
Тб
.
10.03.2023

21.

Сложение взаимно перпендикулярных колебаний одинаковой
частоты
x A1 cos t
y A2 cos t
x
cos t A
1
y cos t cos sin t sin
A2
y
x
cos 1 cos2 t sin
A2 A1
y
x
cos
A2 A1
2
2
x
1 sin
A1
2
2
2
x 2
y
x
2 xy
cos cos 2 1 sin 2
A1 A2
A1
A2
A1
2
2
2
y
x
x
2 xy
cos2 sin 2
cos sin 2
A1 A2
A2
A1
A1
x2
A12
y2
A22
2 xy
cos sin 2
A1 A2
21

22.

Сложение взаимно перпендикулярных
колебаний одинаковой частоты
x A1 cos t
y A2 cos t
x2
y2
2 xy
cos sin 2
A12 A22 A1 A2
В общем случае это уравнение эллипса:
22

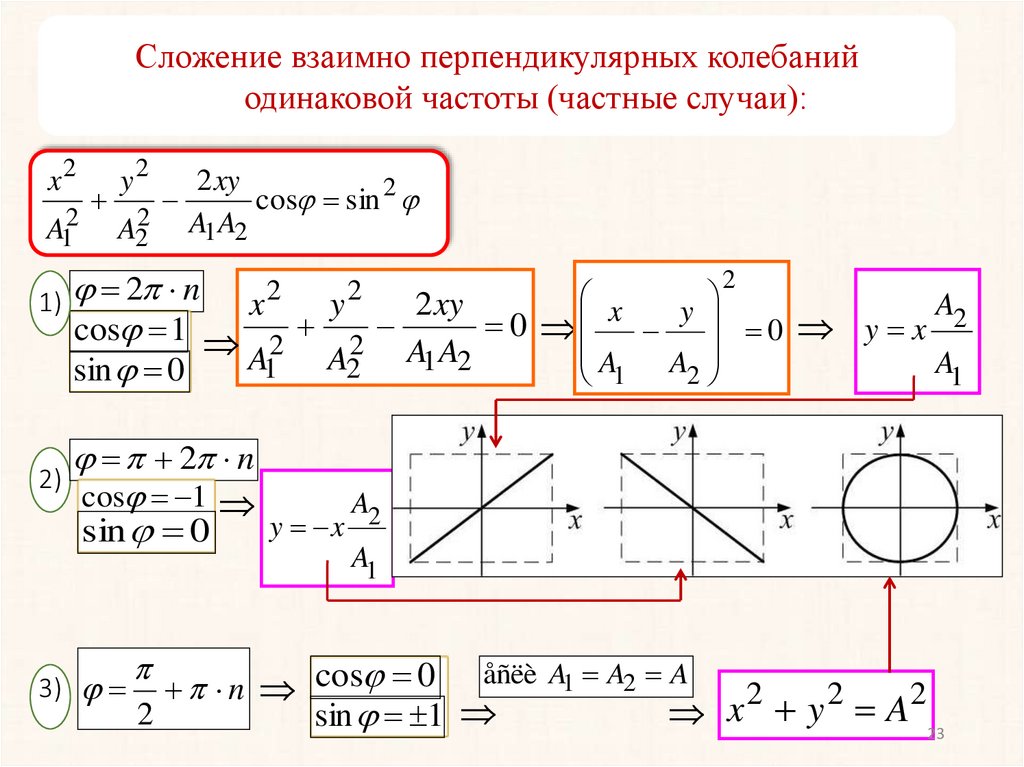
23.

Сложение взаимно перпендикулярных колебаний
одинаковой частоты (частные случаи):
x2
A12
y2
A22
2 xy
cos sin 2
A1 A2
2
2
n
2
2
x
1)
A2
x
y
2 xy
y
0
0 y x
cos 1 2 2
A1 A2 A1 A2
A1
sin 0
A1 A2
2)
2 n
cos 1
sin 0
3)
y x
A2
A1
n cos 0 åñëè A1 A2 A
2
2
2
x
y
A
2
sin 1
23

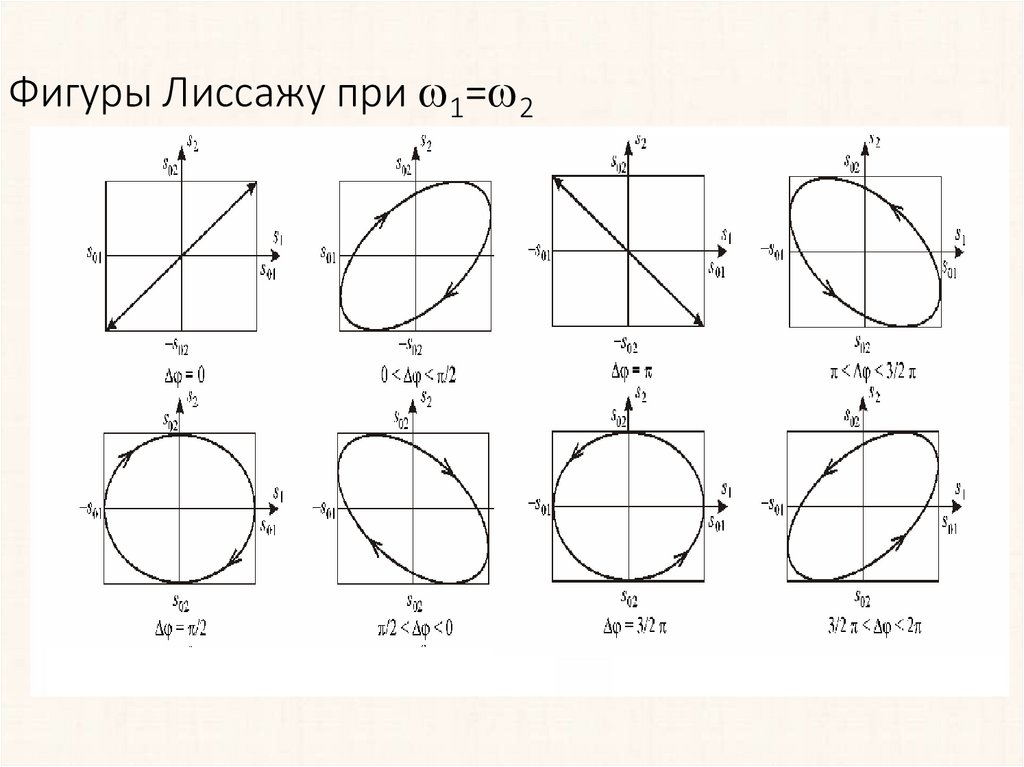
24. Фигуры Лиссажу при 1=2

Фигуры Лиссажу при 1= 2

25.

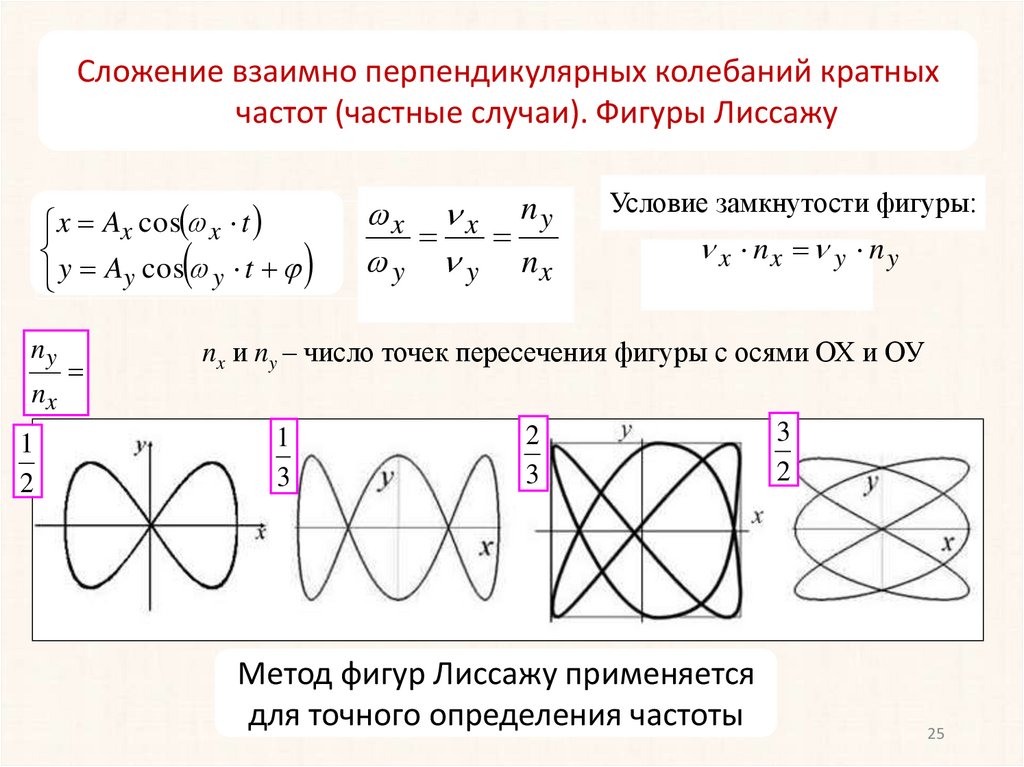
Сложение взаимно перпендикулярных колебаний кратных
частот (частные случаи). Фигуры Лиссажу
x Ax cos x t
y Ay cos y t
ny
nx
1
2
x x ny
y y nx
Условие замкнутости фигуры:
x nx y n y
nx и ny – число точек пересечения фигуры с осями ОХ и ОУ
1
3
2
3
Метод фигур Лиссажу применяется
для точного определения частоты
3
2
25

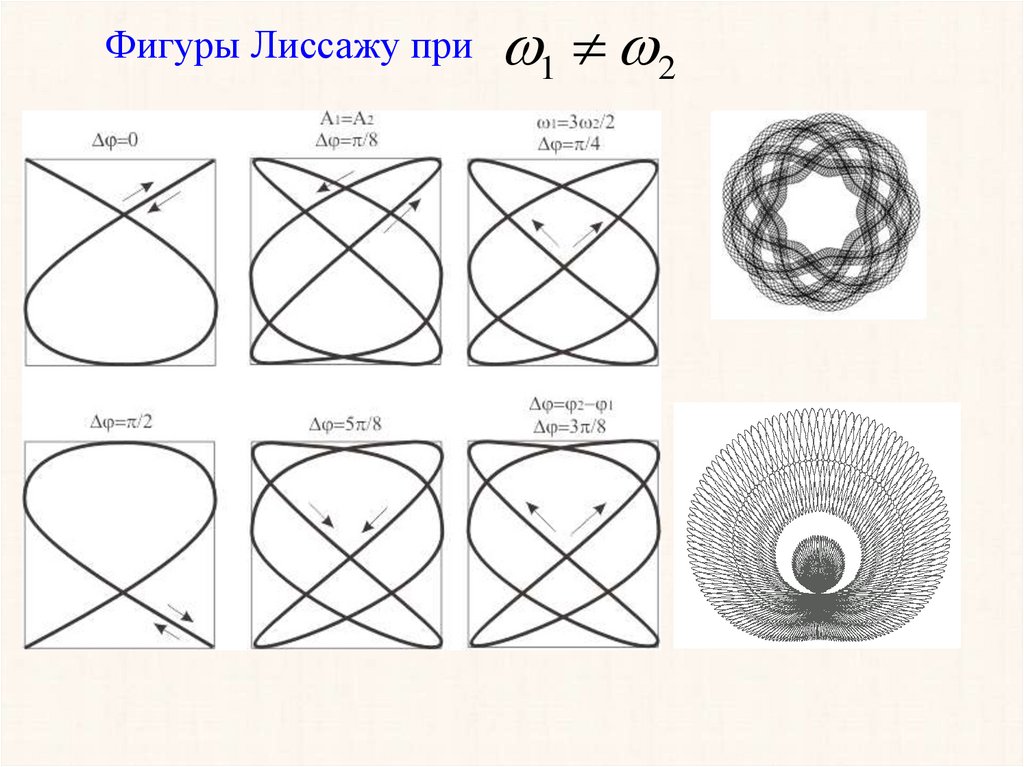
26.

Фигуры Лиссажу при
1
2