Колебания и волны. Гармонические колебания

1. ЛЕКЦИЯ №6 КОЛЕБАНИЯ И ВОЛНЫ

2. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

1. Виды и признаки колебаний
• В физике особенно выделяют колебания двух видов
– механические и электромагнитные и их электромеханические комбинации, поскольку они чрезвычайно
актуальны для жизнедеятельности человека.
• Колебательным движением называются процес-сы,
отличающиеся той или иной степенью повторяемости во времени.
Для колебаний характерно превращение одного вида
энергии в другой – кинетической в потенциальную,
магнитной в электрическую и т.д.
Простейшим примером периодического движения
служат колебания груза на конце пружины.
Будем считать, что массой пружины можно
пренебречь и что пружина установлена горизонтально.

3. о

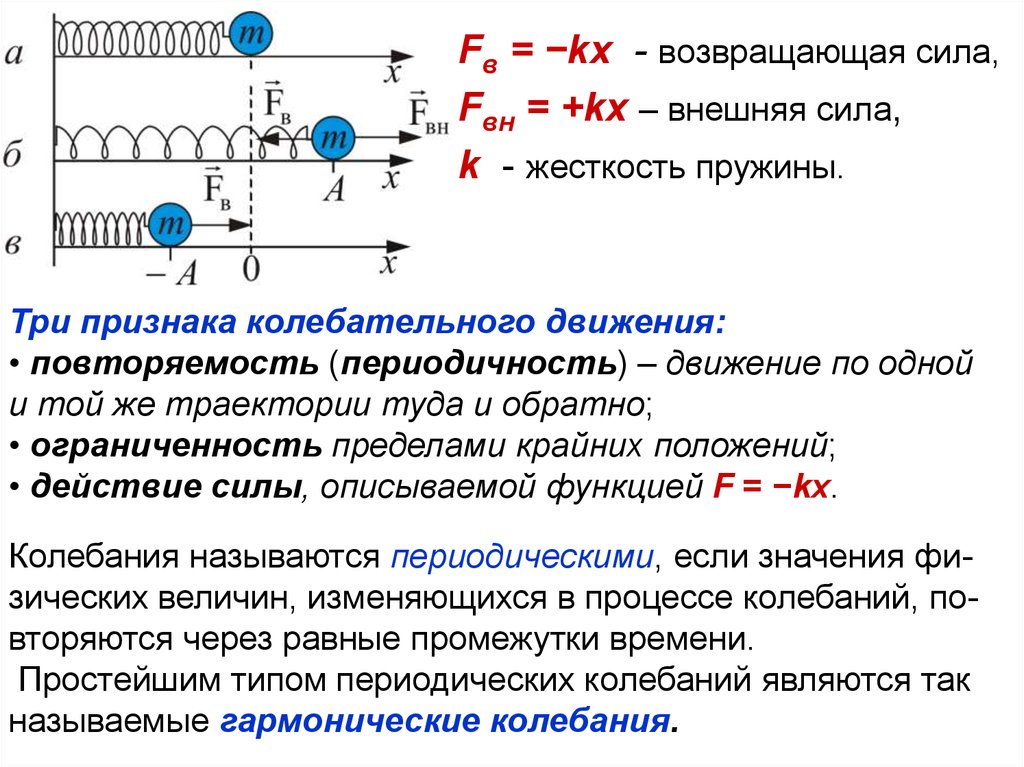
Fв = −kx - возвращающая сила,
Fвн = +kx – внешняя сила,
k - жесткость пружины.
Три признака колебательного движения:
• повторяемость (периодичность) – движение по одной
и той же траектории туда и обратно;
• ограниченность пределами крайних положений;
• действие силы, описываемой функцией F = −kx.
Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
Простейшим типом периодических колебаний являются так
называемые гармонические колебания.

4.

Любая колебательная система, в которой возвращающая сила прямо пропорциональна смещению, взятому
с противоположным знаком (например, F = −kx ), совершает гармонические колебания.
Саму такую систему часто называют гармоническим
осциллятором.
1) Колебания, встречающиеся в природе и технике,
часто имеют характер, близкий к гармоническому;
2)Различные периодические процессы можно представить как наложение гармонических колебаний.
Периодический процесс можно описать уравнением:
f(t) = f (t + nT) .
По определению, колебания называются гармоническими, если зависимость некоторой величины x = f (t)
имеет вид
x = Asin φ или x = Acosφ
(6.1)
Здесь синус или косинус используются в зависимости
от условия задачи, А и φ – параметры колебаний.

5.

2. Параметры гармонических колебаний
• Расстояние груза от положения равновесия до точки, в
которой находится груз, называют смещением x.
• Максимальное смещение – наибольшее расстояние от
положения равновесия – называется амплитудой и обозначается буквой A.
• Выражение, стоящее под знаком синуса или косинуса в
формуле (6.1) φ = ωt + φ0 , определяет смещение x в данный момент времени t и называется фазой колебания.
• При t =0 φ = φ0, поэтому φ0 называется начальной фазой
колебания. Фаза измеряется в радианах и определяет значение колеблющейся величины в данный момент времени.
• Движение от некоторой начальной точки до возвращения в
ту же точку, например от x = A к x = −A и обратно в x = A,
называется полным колебанием.
• Частота колебаний ν определяется как число полных
колебаний в 1 секунду. Частоту, как правило, измеряют в
герцах (Гц): 1 Гц равен 1 полному колебанию в секунду.

6.

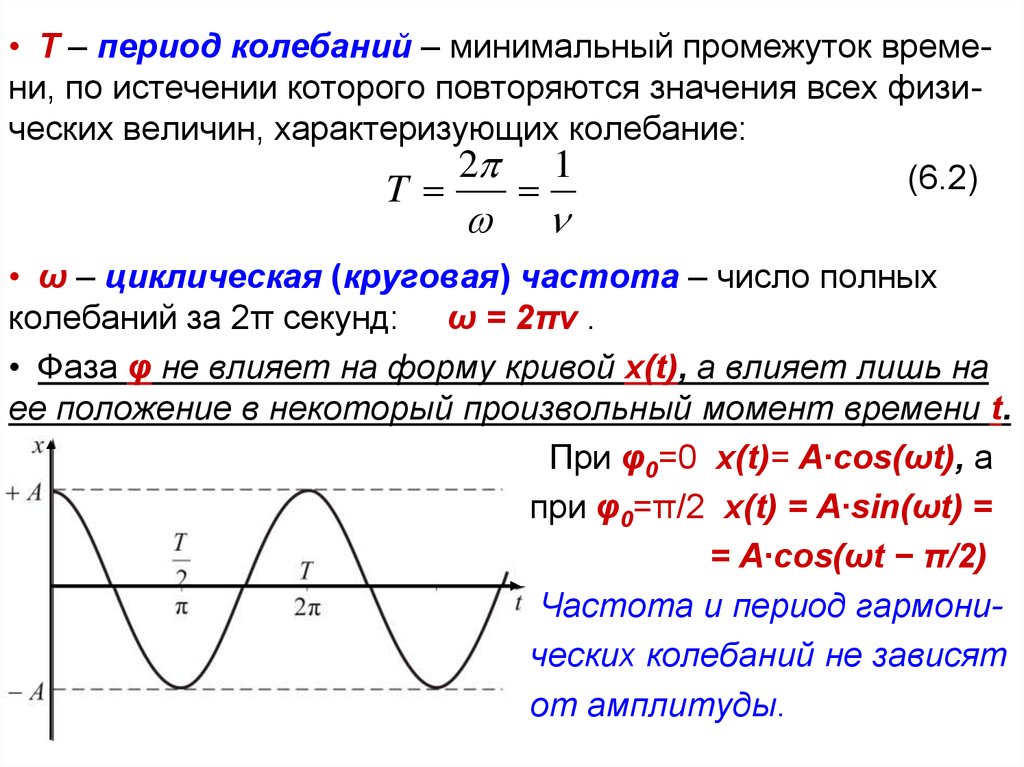
• Т – период колебаний – минимальный промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание:
2 1
(6.2)
T
• ω – циклическая (круговая) частота – число полных
колебаний за 2π секунд: ω = 2πν .
• Фаза φ не влияет на форму кривой х(t), а влияет лишь на
ее положение в некоторый произвольный момент времени t.
При φ0=0 x(t)= A∙cos(ωt), а
при φ0=π/2 x(t) = A∙sin(ωt) =
= A∙cos(ωt − π/2)
Частота и период гармони
ческих колебаний не зависят
от амплитуды.

7.

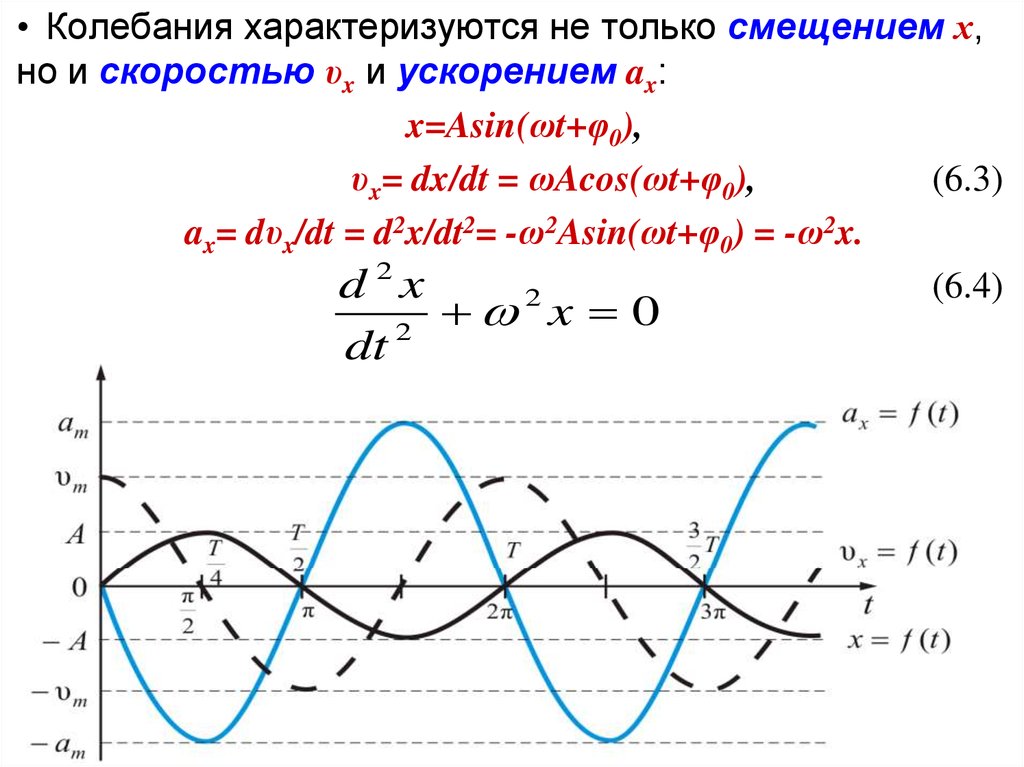
• Колебания характеризуются не только смещением х,
но и скоростью υx и ускорением ax:
x=Asin(ωt+φ0),
υx= dx/dt = ωAcos(ωt+φ0),
(6.3)
ax= dυx/dt = d2x/dt2= -ω2Asin(ωt+φ0) = -ω2x.
(6.4)
d 2x
2
dt
2
x 0

8. 3. Механические гармонические колебания (на примере маятников)

Если физическую систему, обладающую состоянием устойчивого
равновесия, вывести из этого состояния каким-либо внешним воздействием и затем предоставить самой себе, то возникающие в
системе колебания вблизи устойчивого равновесия называют
собственными или свободными.
Способную совершать собственные колебания систему называют
осциллятором. Примером линейных (одномерный случай) осцилляторов могут служить маятники (рис.): а) пружинный (груз
на пружине); б) крутильный (диск на проволоке); в) математический (материальная точка на нерастяжимой нити); г) физический
(С – центр масс твердого тела, О – точка прохождения оси колебаний, перпендикулярной плоскости чертежа).

9.

Рассмотрим случай а)– пружинный маятник.
Второй закон Ньютона для колеблющегося тела для одномерного
случая можно записать в виде: m∙ax = Fx = -k∙x или
d 2x
d 2x
2
k
d
x
2
m 2 k x 0
x 2 x 0
2
dt
m
dt
dt
x = Xmax∙cos(ω0t +φ0)
2
k
m
T
2
0
k
0
m
Система, совершающая колебания под действием квазиупругой силы , называется линейным гармоническим осциллятором (ЛГО).
Кинетическая энергия материальной точки (колеблющегося тела):
m 2 mA2 02 cos2 ( 0t 0 )
Wê
2
2

10.

Потенциальная энергия ( пружинный маятник):
x
x
x
2 2
m
0x
Wï U Fx dx max dx m( 02 x)dx
2
0
Полная механическая
энергия:0
0
mA2 02 sin 2 ( 0t 0 ) mA2 02 cos2 ( 0t 0 ) mA2 02
W Wê Wï
2
2
2
Классическая колеблющаяся точка не может выйти за границы отрезка
[−xmax;+xmax], т.е. находится в потенциальной яме параболической формы.
Колебания Wk и Wn совершаются со сдвигом по фазе на π и, следовательно, полная механическая энергия материальной точки при
свободных незатухающих гармонических колебаниях не изменяется
со временем (const).

11.

г) физический маятник
Физический маятник – твердое тело, которое может совершать
колебания под действием собственной силы тяжести mg вокруг
неподвижной горизонтальной оси, не проходящей через центр
масс тела и называемой осью качания. Центр тяжести маятника
совпадает с его центром масс. Как правило, силой трения в подвесе маятника пренебрегают и момент относительно оси качания
маятника создает только его сила тяжести mg.
При отклонении маятника на угол α момент,
создаваемый силой тяжести равен:
M = mgd sinα .
Согласно основному уравнению динамики
вращательного движения (для тела с моментом инерции I, вращающегося вокруг неподвижной оси в отсутствие трения):
M J J
2
t
2
mgd sin .
При малых α → sinα ≈ α
→
2
t 2
mgd
0
J

12.

Сравнивая с уравнением свободных незатухающих гармонических
колебаний: d2x/dt2 + ω2x = 0 , имеем для физического маятника:
mgd
,
J
J
T 2
.
mgd
Предельным случаем физического маятника является математический маятник - материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести. Вся масса сосредоточена в
центре масс тела. При этом d=l – длина маятника и момент инерции J = ml2. Тогда
mgl
ml
2
g
,
l
l
T 2
g
Длина математического маятника, имеющего такой же период колебаний, что и данный физический маятник, называется приведенной длиной физического маятника. Точка О1, находящаяся на
расстоянии lпр от точки подвеса О маятника, называется центром
качания физического маятника. Точки O и О1 обладают свойством
взаимности, т.е. при перемене их ролей длина и период маятника
останутся прежними.

13.

Свободные гармонические колебания в электрическом
колебательном контуре
Простейшим колебательным контуром является замкнутая цепь,
состоящая из емкости C и катушки индуктивности L.
По закону Ома для замкнутой цепи: сумма падений
напряжений на проводниках сопротивлением R и на
конденсаторе Uс равна ЭДС самоиндукции в контуре
IR + Uc = IR + Q/C = εsi = -L(dI/dt).
I = dQ/dt → dI/dt = d2Q/dt2,
d 2Q
dt
2
R dQ
1
Q 0
L dt
LC
1
LC
,
(R→0) → d2Q/dt2 + ω2Q =0
T 2 / 2 LC.
Q =Qmsin(ωt + φ0) и I = dQ/dt = ωQmcos(ωt + φ0) = Imcos(ωt + φ0)
W = Wэл + Wмагн = (1/2)∙(LI2 + CU2)

14.

4. Способы представления гармонических
колебаний
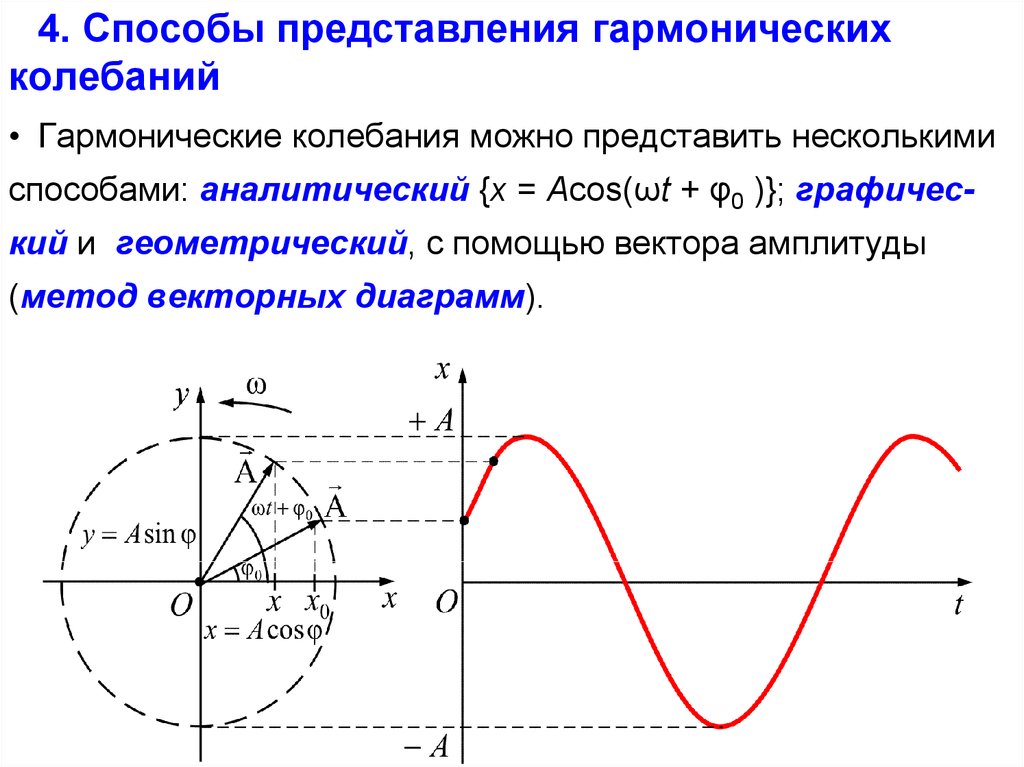
• Гармонические колебания можно представить несколькими
способами: аналитический {x = Acos(ωt + φ0 )}; графический и геометрический, с помощью вектора амплитуды
(метод векторных диаграмм).

15.

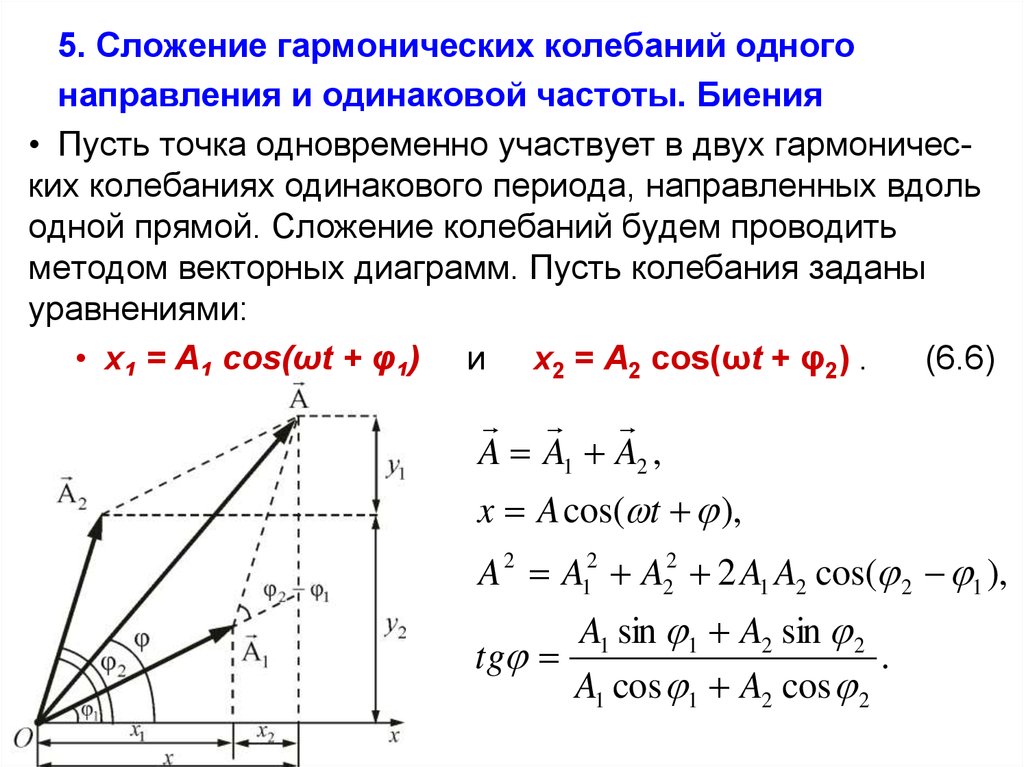
5. Сложение гармонических колебаний одного
направления и одинаковой частоты. Биения
• Пусть точка одновременно участвует в двух гармонических колебаниях одинакового периода, направленных вдоль
одной прямой. Сложение колебаний будем проводить
методом векторных диаграмм. Пусть колебания заданы
уравнениями:
• x1 = A1 cos(ωt + φ1) и x2 = A2 cos(ωt + φ2) .
(6.6)
A A1 A2 ,
x A cos( t ),
A 2 A12 A22 2 A1 A2 cos( 2 1 ),
A1 sin 1 A2 sin 2
tg
.
A1 cos 1 A2 cos 2

16.

1) Разность фаз равна нулю или четному числу π, то есть
φ2 − φ1 = 2πm, где m = 0, ±1, ± 2, ± 3, .... Тогда cos(φ2 − φ1)
=1 и A = A1 + A2 (колебания синфазны).
2) Разность фаз равна нечетному числу π, то есть φ2 − φ1=
= π(2m +1) , где m = 0, ±1, ± 2, ± 3, .... Тогда cos(φ2 − φ1) = −1.
Отсюда A =|A2 − A1| (колебания в противофазе).

17.

Когерентными называются колебания, разность фаз которых во
времени постоянна; т.к. ∆Ф(t) = (ω2 − ω1)t + (ϕ2 − ϕ1 ) = const , то
это выполняется при ω2= ω1= ω, тогда x = x1+ x2= Asin(ωt+ϕ), где
А амплитуда и Ф=(ωt+ϕ) фаза результирующего колебания. Тогда
в зависимости от значения (ϕ2 −ϕ1) результирующая амплитуда А
изменяется в пределах от A = |A1 − A2| при ϕ2 -ϕ1 = ±(2m +1)π, до A
= |A1 + A2| при ϕ2 -ϕ1 = ±2 π m (m → целые числа).
При ϕ2 -ϕ1 = ±2 π m колебания называются синфазными (в одной
фазе), а при ϕ2 -ϕ1 = ±(2m +1)π – противофазными.
При ω1 ≠ ω2 результирующий вектор A будет изменяться по длине
и вращаться с переменной скоростью. При сложении колебаний с
близкими частотами (Δω=|ω2 −ω1|<<ω) возникают, так называемые, биения, тогда x1 = Acosωt,
x2 = Acos(ωt + Δωt).
x(t ) x1 x 2 2 A cos
t t t
cos
t t t
2
t
2 A cos t cos
Aá cos t
2
2

18.

[2ωt >>Δω; cos(-Δωt)=cos(Δωt)]
t
Aá 2 A cos
2
x(t ) Aá cos t
Косинус берется по модулю, так как функция четная и поэтому
частота биений ωб = Δω, а не Δω/2. Период биений равен половине периода модуляции:
Тб = Тмод /2 = 2π/(Δω)

19.

Вообще, колебания вида x = A(t)cos[ωt + φ(t)] называются
модулированными. Частные случаи: амплитудная модуляция и модулирование по фазе или частоте. Биение –
простейший вид модулированных колебаний.
Любые сложные периодические колебания S=f (t) можно
представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами,
начальными фазами, а также частотами, кратными циклической частоте ω:
S (t ) f (t )
A0
A1 cos( t 1 ) A2 cos(2 t 2 ) An cos(n t n )
2
Представление периодической функции в таком виде
связывают с понятием гармонического анализа сложного
периодического колебания, или разложения Фурье (то есть
представление сложных модулированных колебаний в виде
ряда (суммы) простых гармонических колебаний). Слагаемые
ряда Фурье, определяющие гармонические колебания с частотами ω, 2ω, 3ω, ..., называются первой (или основной),
второй, третьей и т.д. гармониками сложного
периодического колебания.

20.

6. Сложение взаимно перпендикулярных колебаний
Пусть некоторое тело колеблется и вдоль оси x, и вдоль оси
y, т.е. участвует в двух взаимноперпендикулярных колебаниях: x = A1 cos(ω1t + φ1) ; y = A2 cos(ω2t + φ2 ) .
Найдем уравнение результирующего колебания. Для простоты примем ω1 = ω2 = ω. Разность фаз между обоими колебаниями равна: Δφ = φ2 − φ1 . Чтобы получить уравнение
траектории, надо исключить из этих уравнений время t.
Упростим выражения, выбрав начало отсчета так, чтобы
φ1 = 0 , т.е.
x = A1 cosωt ; y = A2 cos(ωt + Δφ) .
2
x
x
cos t или
A1
sin t 1
A12
y
x
x2
cos t cos sin t sin 2 cos sin 1 2 .
A2
A1
A1

21.

2
y
x
x
cos
sin
1
2
A1
A1
A2
Возведем обе части в квадрат, сгруппируем и получим
окончательное уравнение:
2
2
2
2
y
x
2 xy
2
cos(
)
sin
( 2 1 ).
2
1
2
2
(6.7)
A2 A1 A1 A2
В результате мы получили уравнение эллипса, оси которого
ориентированы относительно x и y произвольно.

22.

Рассмотрим частные случаи решения уравнения (6.7)
1. Начальные фазы колебаний одинаковы: φ1 = φ2 , т.е.
φ2 − φ1 = 0. Тогда уравнение (6.7) примет вид:
2
2
y
x
2 xy
2
0
2
A1 A2
A2
A1
2
x
A2
y
x.
0 y
A1
A1 A2
Получили уравнение прямой, проходящей через начало координат. Следовательно, в результате сложения двух взаимно перпендикулярных колебаний с
одинаковыми начальными
фазами будут происходить
колебания вдоль прямой,
проходящей через начало
координат.

23.

7. Свободные затухающие механические колебания
Все реальные колебания являются затухающими. Энергия
механических колебаний постепенно расходуется на работу
против сил трения и амплитуда колебаний постепенно уменьшается (затухает). Во многих случаях в первом приближении
можно считать, что при небольших скоростях силы, вызывающие затухание колебаний, пропорциональны величине скорости (например маятник). Тогда сила трения (или сопротивления):
Fтр = -r∙v,
где r – коэффициент сопротивления, v – скорость движения.
d 2x
dx
ma x kx rv x m 2 kx r ,
dt
dt
d 2 x r dx k
x 0,
2
m dt m
dt
r
k
; 02 .
2m
m

24.

Однородное дифференциальное уравнение второго порядка, описывающее затухающее колебательное движение, запишется в виде:
d 2x
dx
2
dt
2
2
dt
0 x 0.
Решение этого уравнения имеет вид:
x A0 e t cos( t 0 )
• Здесь А0 и φ0 определяются из краевых условий задачи
(начальных и граничных), а β и ω – из самого уравнения.
2
0
2
0
T
2
2
02 2
.
• где ω0 – круговая частота собственных колебаний (без
затухания); ω – круговая частота свободных затухающих
колебаний.
k
r
k r
0
;
;
m
2m
m 2m
2

25.

t
t
A0 e
A(t )
e
T
e
.
( t T )
t
T
A(t T ) A0 e
e e
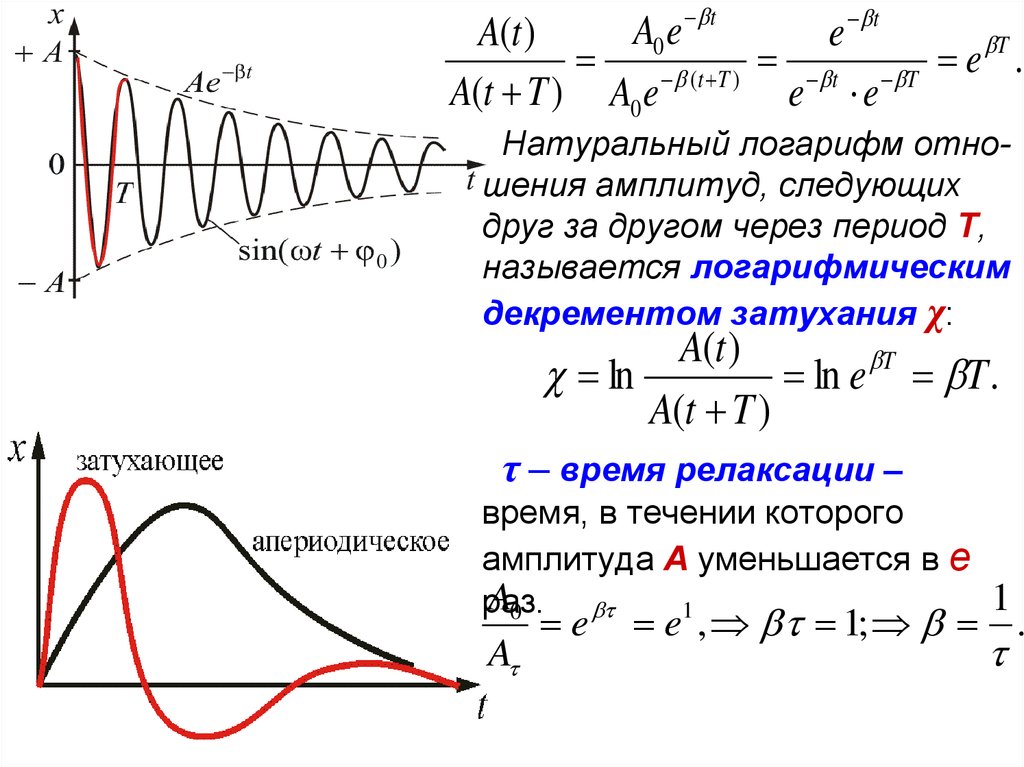
Натуральный логарифм отношения амплитуд, следующих
друг за другом через период Т,
называется логарифмическим
декрементом затухания χ:
A(t )
T
ln
ln e T .
A(t T )
τ – время релаксации –
время, в течении которого
амплитуда А уменьшается в е
A0
1
раз.
1
A
e
e , 1; .

26.

Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого
амплитуда уменьшается в е раз.
Пусть N число колебаний, после которых амплитуда уменьшается в e раз. Тогда:
τ = NТ;
→ T = τ/N; →β = 1/τ
1
T
N N .
Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e
раз.