Похожие презентации:
Движение тел с переменной массой
1. Движение тел с переменной массой
Импульс системы:P MVС
Полный импульс системы частиц равен произведению
полной массы системы М на скорость её центра масс VС .
Рассмотрим движение тел с переменной массой на примере
движения ракеты, которая движется вперед за счет
выбрасывания назад сгоревших газов.
Ракета ускоряется силой, действующей на нее со стороны газов.
Масса М ракеты все время уменьшается, т.е.
dM / dt 0
U
v
2.
Реактивное движение основано на принципе отдачи. Вракете при сгорании топлива газы, нагретые до высокой
температуры, выбрасываются из сопла с большой скоростью
относительно ракеты u
Пусть M(t), υ(t), Mυ(t) – масса, скорость и импульс ракеты в
момент времени t.
Спустя время dt масса ракеты уменьшится на dM, скорость
увеличится на dυ, а изменение импульс системы станет равным
M dM d udm Г M Fdt ,
где udmГ – импульс газов, образовавшихся за время dt.
3.
Воспользуемся законом сохранения массы:dmГ dM
Получим:
d dM
M
u
F
dt
dt
dM
, добавляемая к силе F
Величина u
dt
– реактивная сила, т.е. сила, с которой действуют на ракету
вытекающие из нее газы.
Уравнение
d dM
M
u
F
dt
dt
впервые получено русским механиком Мещерским И.В. и носит
название уравнение Мещерского.
4.
При отсутствии внешних сил, действующих наракету, уравнение приобретает вид:
d dM
M
u
dt
dt
Решение этого уравнения дает конечную скорость
ракеты:
M0
u ln
,
M
5.
М0 и М – начальная и конечная массы ракеты.Соотношение
M0
р u ln
M
называют формулой Циолковского.
Из нее следует, что для достижения скорости υ, в 4
раза превышающей по модулю относительную скорость
выбрасываемых газов, стартовая масса одноступенчатой
ракеты должна, примерно в 50 раз, превышать ее
конечную массу.
6.
7.
Из словаря В.Даля:Работа - труд, занятие, дело, упражнение, т.е. всякое
полезное действие человека или устройства. Все, что
требует усилий, старанья, напряжения телесных или
умственных сил.
8.
Что такое механическая работа?В физике этот термин имеет более узкое значение. Им обозначается
физическая величина, связанная с действием сил.
Термин «механическая работа» был
введен в физику в 1826 г. французским
ученым Ж. Понселе: «Механическая
работа — это постоянное преодоление
сопротивлений силой, действующей
вдоль пути»
Жан Виктор Понселе
01.07.1788 г. 22.12.1867г.
9. Джеймс Прескотт Джоуль (24 декабря 1818— 11 октября 1889)
Джоуль изучал природу тепла иобнаружил её связь с
механической работой. Это
привело к теории сохранения
энергии.
В честь Джоуля названа единица
измерения механической
работы и энергии — джоуль.
10.
Механическая работаМеханическая работа – скалярная физическая величина,
характеризующая движение тела под действием силы и равная
скалярному произведению вектора силы на вектор перемещения.
Элементарная работа:
dA F dr ,
А 1Н м 1 Дж
Знак работы:
π
0 α , dA 0
2
, dA 0
dA Fdr cos FS ds
dA Fx dx Fy dy Fz dz
dA F dt dp mvdv
2
π
α , dA 0
2
Работа при перемещении 1-2 :
2
2
2
1
1
1
A dA FS ds FS υdt
Работа численно равна площади под графиком
проекции силы на направление перемещения:
На основе III закона Ньютона работа
силы и работа против силы противоположны по
знаку:
F F
dA dA
1, 2
2 ,1
1
2
11.
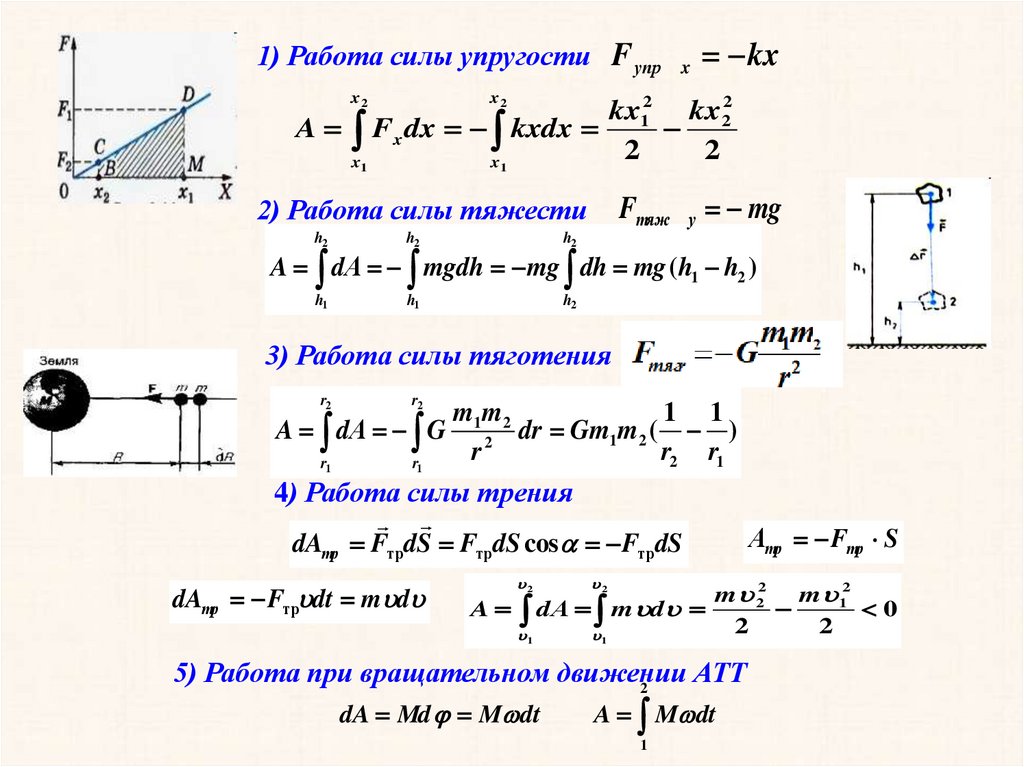
1) Работа силы упругости F упрx2
x
kx
x2
kx12 kx 22
A Fx dx kxdx
2
2
x1
x1
Fтяж у mg
2) Работа силы тяжести
h2
h2
h2
h1
h1
h2
A dΑ mgdh mg dh mg ( h1 h2 )
3) Работа силы тяготения
r2
r2
r1
r1
A dΑ G
m1 m 2
1 1
dr
Gm
m
(
)
1 2
r2
r2 r1
4) Работа силы трения
dAтр FтрdS FтрdS cos FтрdS
dAтр Fтр dt m d
2
2
Атр Fтр S
m 22 m 12
A dΑ m d
0
2
2
1
1
5) Работа при вращательном движении
АТТ
2
dA Md M dt
A M dt
1
12. Мощность
Мощность - скалярная физическая величина,характеризующая быстроту совершения работы и равная
работе, совершаемой за единицу времени.
Средняя мощность определяется отношением работы ко времени, за
которое она была совершена:
N cp
A
F Vср ,
t
N 1 Дж 1Вт
1с
Мгновенная мощность равна производной от величины работы по времени:
dA d ( F r ) F dr
N
F V F V cos α ,
dt
dt
dt
F const
При известной мощности работа определяется выражениями:
A N ср t , dA N dt ,
A Ndt
s
13. Энергия
Энергия – скалярная физическая величина, являющаяся единой мерой различныхформ движения материи и характеризующая их способность к взаимному
превращению.
Энергия – конечная, однозначная, непрерывная, аддитивная
функция параметров состояния системы.
Формам движения материи соответствуют виды энергии:
Механическая
Внутренняя (тепловая)
Электромагнитная
Ядерная….
Закон сохранения энергии: в замкнутой системе тел энергия может
переходить от одних тел к другим, превращаться из одних видов в другие,
но её суммарное значение остаётся неизменным.
14. Механическая энергия
Механическая энергия – скалярная физическая величина,мера механического движения тела, изменение которой
определяется работой действующих на тело сил.
Механическая энергия (W) - функция параметров
механического состояния: r ,V или r , p
W f ( r ,V ) f ( r , р )
W f ( x , y , z , p x , p y , pz )
Различают: кинетическую, обусловленную движением, и
потенциальную, связанную с взаимодействием,
составляющие механической энергии.
W Wкин Wпот
15. Кинетическая энергия
Кинетическая энергия, Wкин (V),- часть механической энергии,обусловленная движением тела и зависящая от его
скорости (импульса).
Особенности кинетической энергии:
положительность, аддитивность, относительность.
Теорема об изменении кинетической энергии:
Изменение кинетической энергии тела равно работе
равнодействующей всех сил, приложенных к телу.
2
dv
m 22 m 12
Aр всех сил F p dr m v dt m d
Wкин 2 Wкин 1 Wкин
dt
2
2
1
Поступательное движение
m 2
p2
Wкин
2
2m
Вращательное движение
J 2
L2
Wкин
2
2J
16. Потенциальная энергия
Потенциальная энергия, Wпот (r), – часть механическойэнергии, обусловленная взаимодействием тел или их частей
и зависящая от положения тела в пространстве.
Особенности потенциальной энергии:
-может быть как положительна, так и отрицательна,
-её численное значение зависит от выбора нулевого уровня,
- расчётная формула определяется характером
взаимодействия.
17. Потенциальная энергия тела
1.Потенциальная энергия при действии силы упругостиkx12 kx22
Aупр
Wпот1 Wпот 2 Wпот
2
2
kx 2
Wпот
, W 0 при х 0
2
18.
2. Потенциальная энергия тела в поле силы тяжестиAтяж mgh1 mgh2 W пот1 Wпот 2 ΔWпот
Wпот mgh,
Wпот 0 при h 0
19.
3.Потенциальная энергия тела в поле гравитации (силытяготения)
Mm
Mm
Aтяг G
G
Wпот 1 Wпот 2 Wпот
r2
r1
Wпот G
Mm
, Wпот 0
r
при r
20. Изменение потенциальной энергии
Потенциальную энергию тела обуславливает потенциальное поле сил, зависящихот положения в нём тела : гравитационное поле, электростатическое поле, поле
упругих сил, поле сил тяжести…
С потенциальным
полем связаны консервативные силы, зависящие от положения
тел, F( x , y , z ) F( r ) , работа которых не зависит от формы траектории, а определяется
лишь начальным и конечным положением тела в потенциальном поле.
Работа консервативной силы при перемещения тела по замкнутой траектории
равна нулю.
A12
конс
2
2
2
1a
1b
1c
dAконс dAконс dAконс
Aконс dAконс 0
1 2 1
Консервативные силы: тяжести, тяготения, упругости, электростатические силы...
Работа консервативной силы равна убыли потенциальной энергии.
r2
dAконс dWпот
Aконс Fdr Wпот(r 1 ) Wпот(r 2 ) Wпот 1 Wпот 2 Wпот
r1
21. Связь консервативной силы с потенциальной энергией
Выразим работу потенциальной силы через убыль потенциальной энергии:dA Fx dx Fy dy Fz dz dWпот
Полный дифференциал функции трёх переменных dWx,y,z :
dWпот
( x , y ,z )
Wпот
W пот
Wпот
dx
dy
dz
x
y
z
Видим, что проекции вектора силы на координатные оси равны соответствующим
частным производным от потенциальной энергии тела с противоположным знаком:
dWпот
Wпот
Wпот
Fz
Fy
dz
x
y
Wпот Wпот Wпот
F (
i
j
k)
F Wпот
x
y
z
Fx
Вектор силы
i
j
k
x
y
z
оператор
градиента
Градиент функции– вектор, характеризующий быстроту изменения функции в
пространстве. Он направлен в сторону наиболее быстрого возрастания функции.
Действующая на тело в потенциальном поле сила равна по модулю и
противоположна по направлению градиенту потенциальной энергии тела.
22. Закон сохранения энергии в механике
Изменение механической энергии системы тел определяется работойвнутренних и внешних сил (консервативных, неконсервативных).
W Wкин Wпот
dWпот dAконс
d (Wкин Wпот ) dAнеконс dAвнеш
dWкин dAр dАконс dAнеконс dAвнеш
dW dAнеконс dAвнеш
Изменение полной механической энергии системы равно алгебраической
сумме работ всех неконсервативных и внешних сил, действующих на тела
системы.
Закон сохранения энергии в механике: полная механическая
энергия замкнутой консервативной системы тел есть
величина постоянная.
dAнеконс 0; dAвнеш 0
dW 0
W const
Wкин Wпот const
23. Закон сохранения механической энергии
Пример 1. Свободное падение- движение под действием силы тяжести при отсутствиисил сопротивления
mυ 2
mgh
const
2
mv 32
m υ22
mgh1 mgh2
2
2
Пример 2. Абсолютно упругий удар- удар, при котором сохраняется механическая
энергия системы:
Закон сохранения энергии
2
2
mυ01
mυ02
mυ12
mυ22
2
2
2
2
Закон сохранения импульса
mυ01 mυ02 mυ1 mυ2
24. Закон сохранения механической энергии
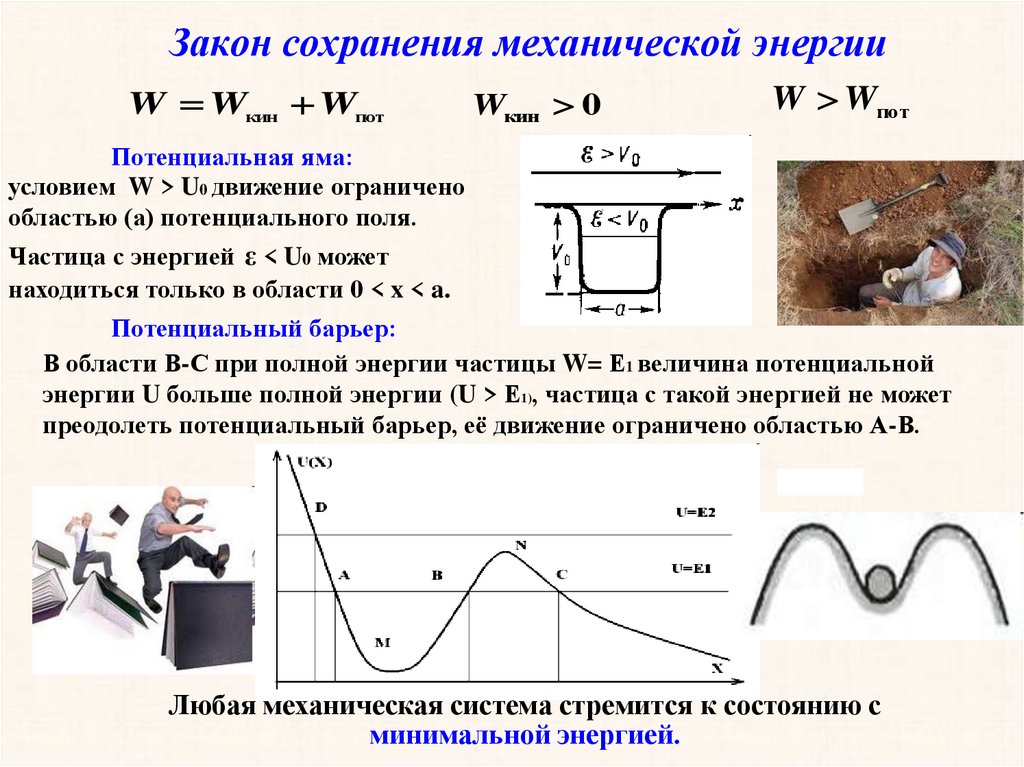
W Wкин WпотWкин 0
W Wпот
Потенциальная яма:
условием W > U0 движение ограничено
областью (а) потенциального поля.
Частица с энергией ε < U0 может
находиться только в области 0 < x < a.
Потенциальный барьер:
В области В-С при полной энергии частицы W= Е1 величина потенциальной
энергии U больше полной энергии (U > Е1), частица с такой энергией не может
преодолеть потенциальный барьер, её движение ограничено областью А-В.
Любая механическая система стремится к состоянию с
минимальной энергией.
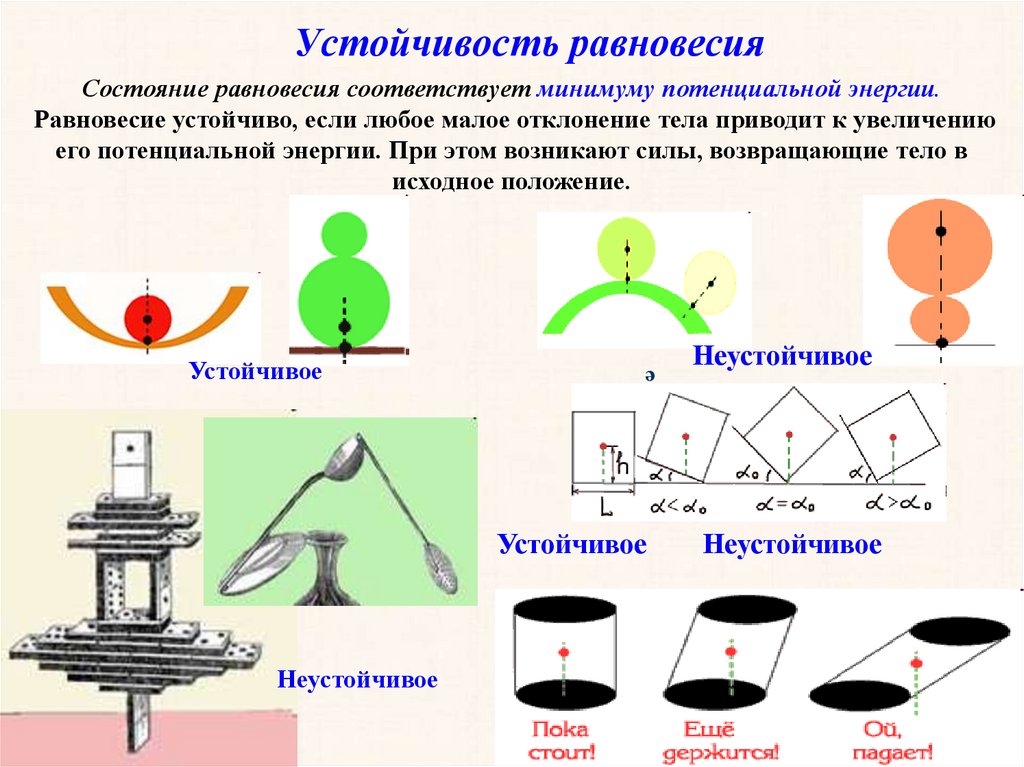
25. Устойчивость равновесия
Состояние равновесия соответствует минимуму потенциальной энергии.Равновесие устойчиво, если любое малое отклонение тела приводит к увеличению
его потенциальной энергии. При этом возникают силы, возвращающие тело в
исходное положение.
е
Устойчивое
Устойчивое
Неустойчивое
Неустойчивое
Неустойчивое






















 Физика
Физика








