Расчет трёхшарнирной арки. Расчетно-графическая работа №2

1.

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 2
«Расчет трёхшарнирной арки»

2.

Исходные данные
Лист 1
l = 40 м, f = l/5 = 8 м, q = 6 кН/м, P = 75 кН,
очертание оси – дуга окружности
y
2
l
R z R f ,
2
2
l 2z cos y R f
sin
,
R
2R
поперечное
сечение
h
h = 0,75 м
f l
R ,
2 8f
b = h/ 4
b
2
R = 10 МПа

3.

Лист 2

4.

Лист 2

5.

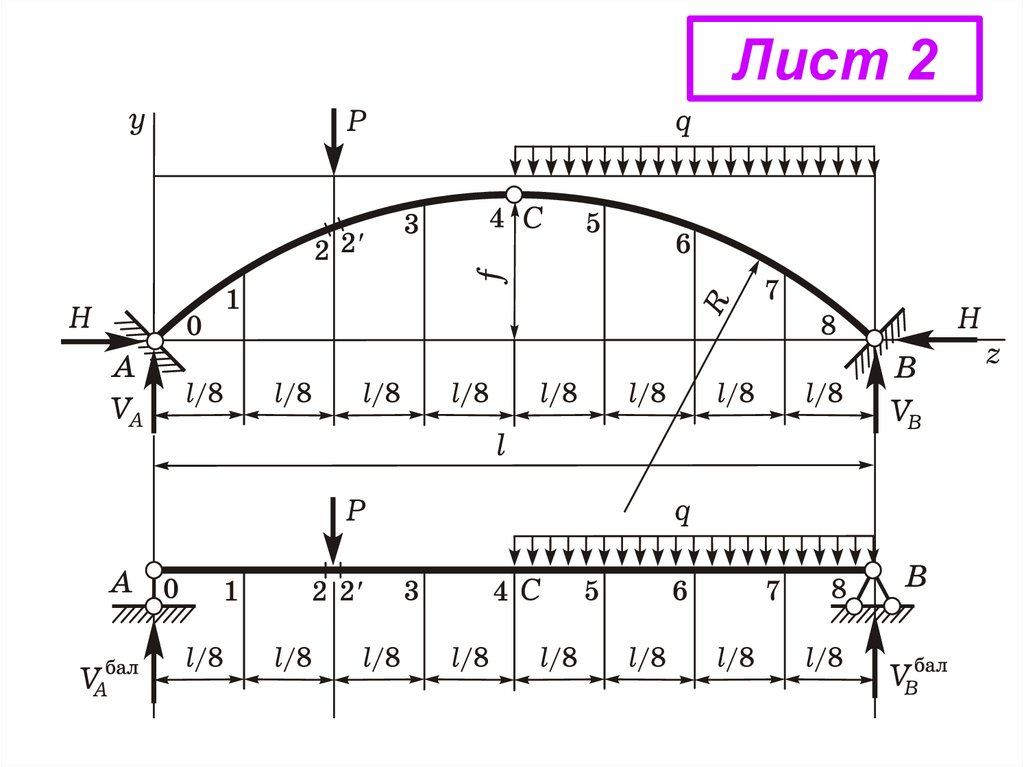
1. Геометрические
параметры оси арки
Лист 1
Наметим на оси арки расчетные сечения k = 0, …, 8.
Положение k-го сечения характеризуется тремя
геометрическими параметрами:
l
абсциссой zk k
8
ординатой
2
l
yk R z k R f
2
2
углом наклона касательной к оси арки k
l 2 zk
sin k
2R
l 2 zk
k arcsin
2R
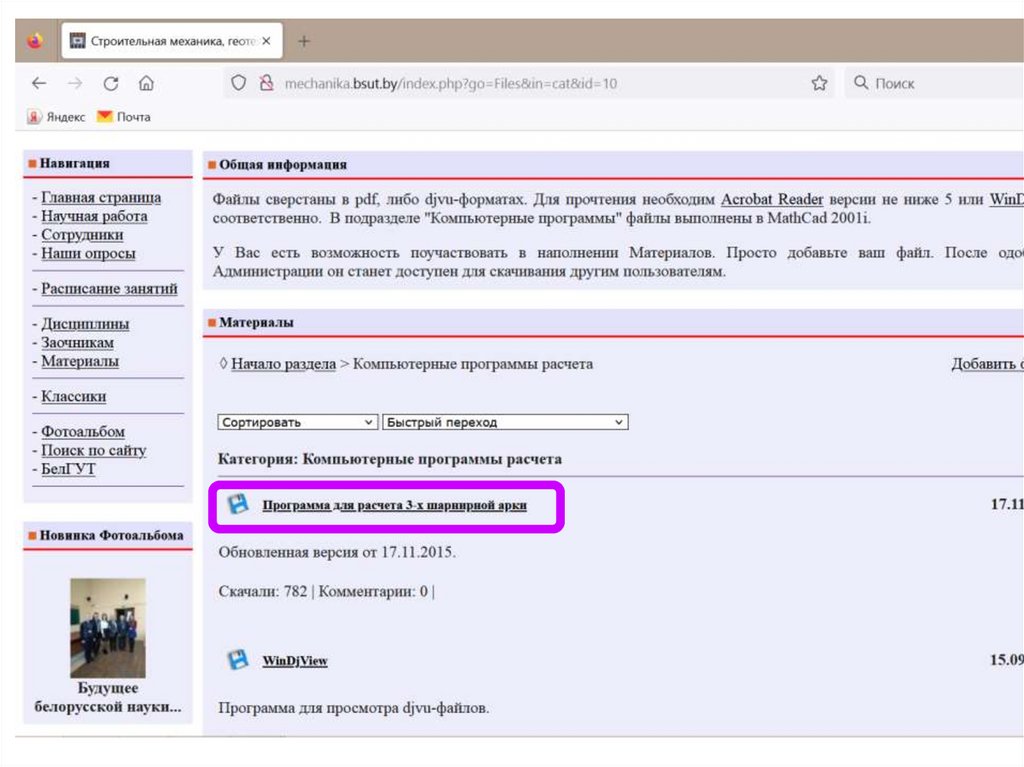
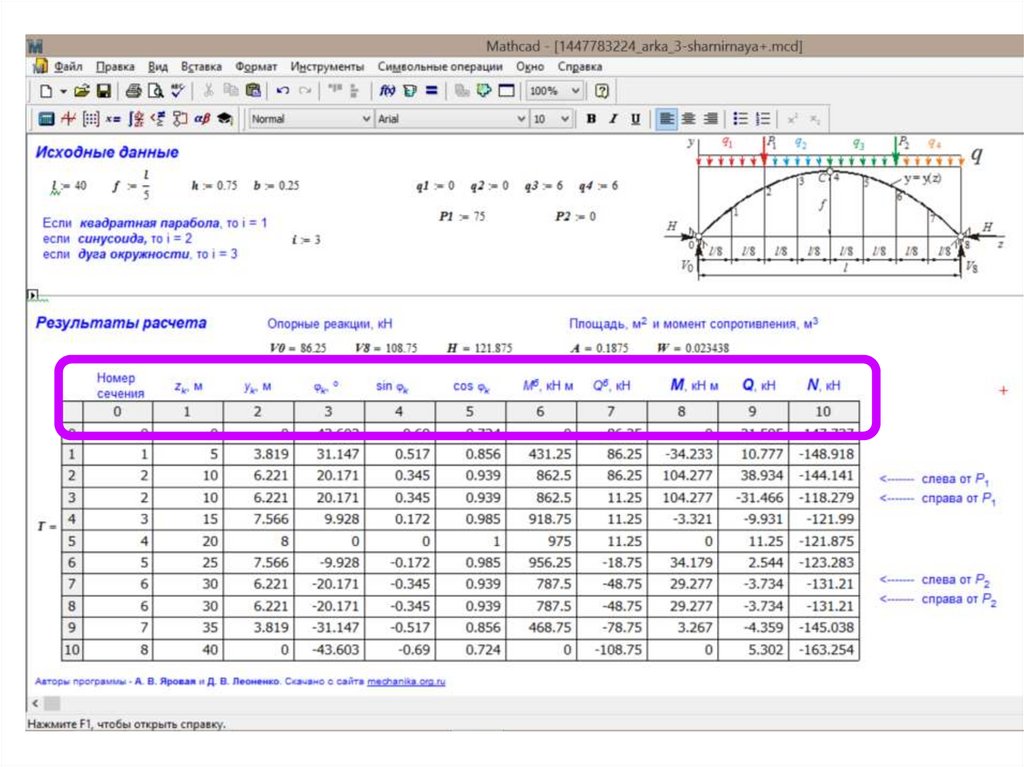
Расчет выполняем с помощью программы в MathCad

6.

7.

8.

Растянуть!!!

9.

10.

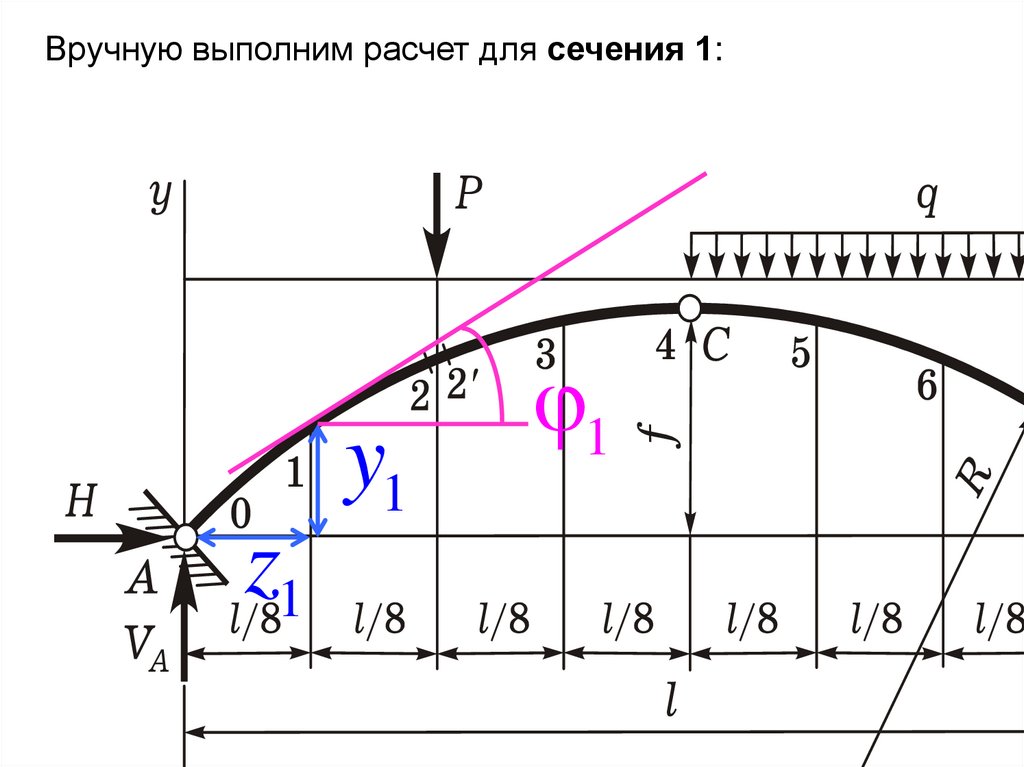
Вручную выполним расчет для сечения 1:
y1
z1
1

11.

k 1:
l
40
z1 1 1 5 м,
8
8
2
2
f l
8 40
R
29 м,
2 8 f 2 8 8
2
l
y1 R z1 R f ......... м
2
l 2 z1
1 arcsin
..........
2R
2

12.

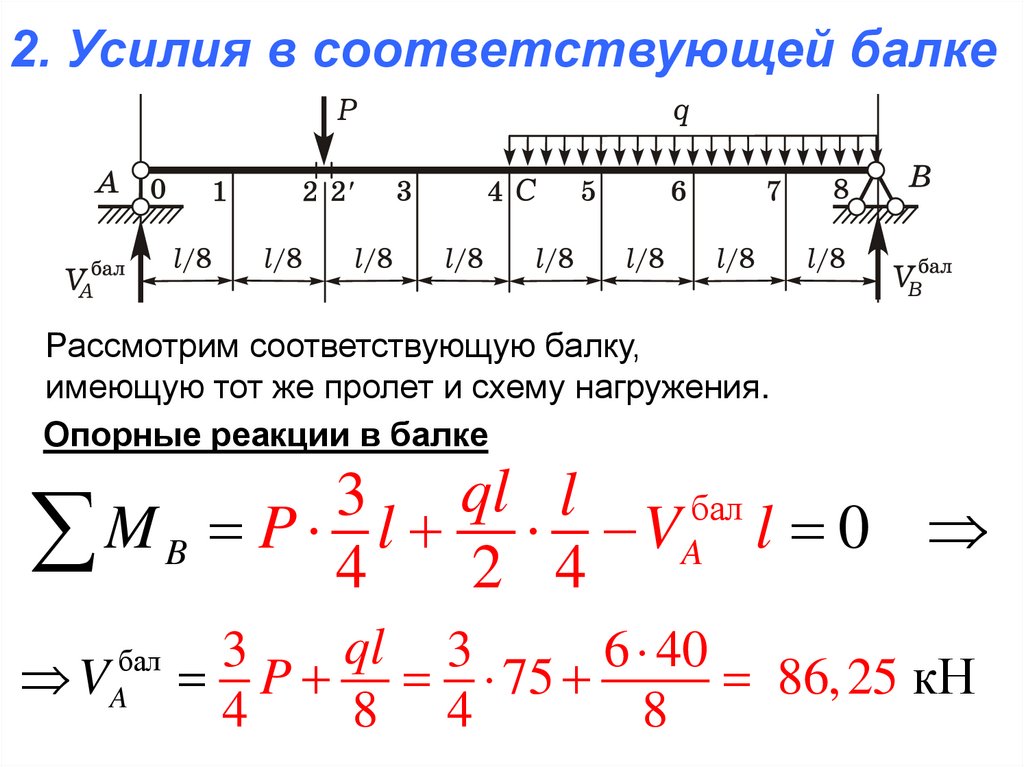
2. Усилия в соответствующей балке
Рассмотрим соответствующую балку,
имеющую тот же пролет и схему нагружения.
Опорные реакции в балке
3 ql l
бал
M B P 4 l 2 4 VA l 0
V
бал
A
ql 3
3
6 40
P 75
86, 25 кН
4
8 4
8

13.

l ql 3l
бал
M A P 4 2 4 VB l 0
P 3ql 75 3 6 40
V
108,75 кН
4
8
4
8
бал
бал
Проверка:
Y VA VB ql / 2 P
бал
B
86, 25 108,75 6 40 / 2 75 0

14.

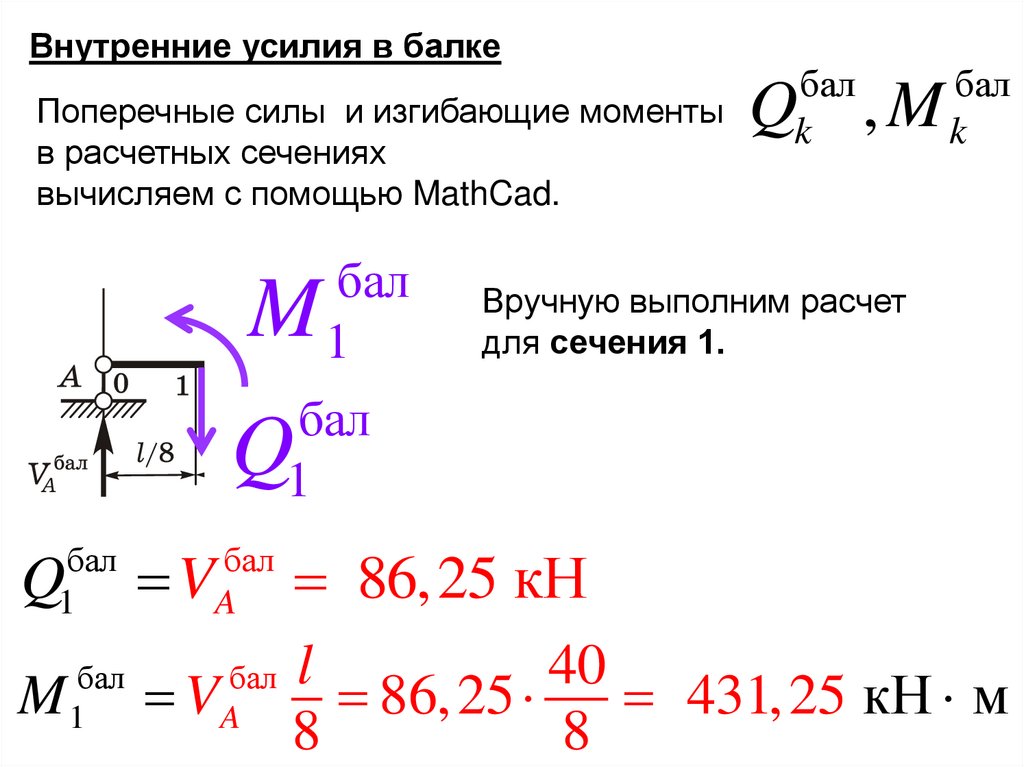
Внутренние усилия в балке
Поперечные силы и изгибающие моменты
в расчетных сечениях
вычисляем с помощью MathCad.
M
бал
1
бал
k
Q ,M
бал
k
Вручную выполним расчет
для сечения 1.
бал
1
Q
бал
1
V
бал
1
V
Q
M
бал
A
бал
A
86,25 кН
l
40
86, 25
431, 25 кН м
8
8

15.

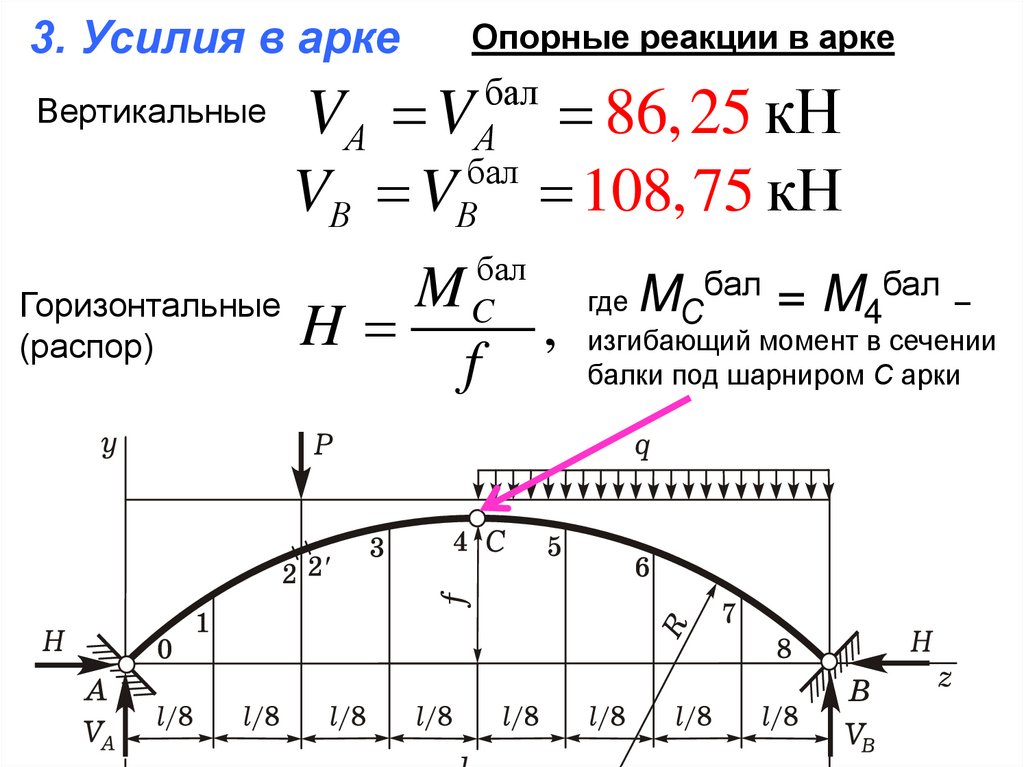
3. Усилия в арке
Вертикальные
Горизонтальные
(распор)
Опорные реакции в арке
VА V
VВ V
бал
А
бал
В
бал
C
M
H
f
86, 25 кН
108,75 кН
,
M бал = M бал
где
–
С
4
изгибающий момент в сечении
балки под шарниром С арки

16.

M
бал
4
l
l
M V
P
2
4
40
40
86, 25 75
975 кН м
2
4
бал
4
Тогда распор
бал
A
бал
4
M
H
f
975
121, 88 кН
8

17.

Внутренние усилия в арке
Усилия в сечениях k = 0, …, 8 определим по формулам
M k M H yk
Qk Q cos k H sin k
бал
k
бал
k
бал
k
Nk Q
sin k H cos k
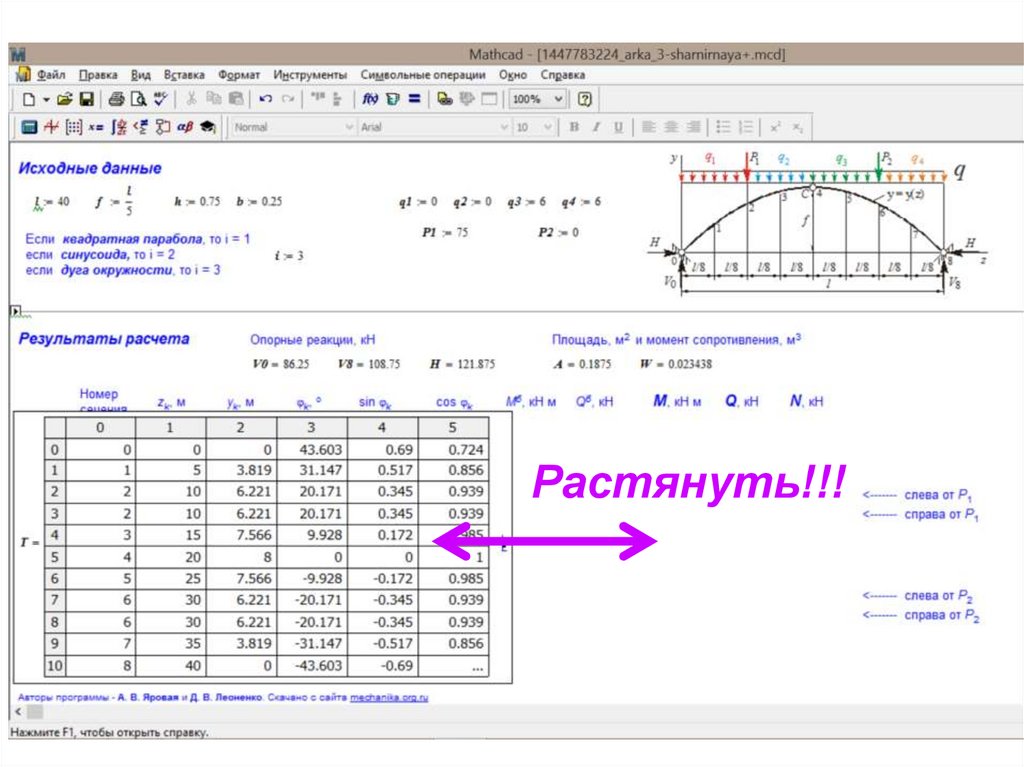
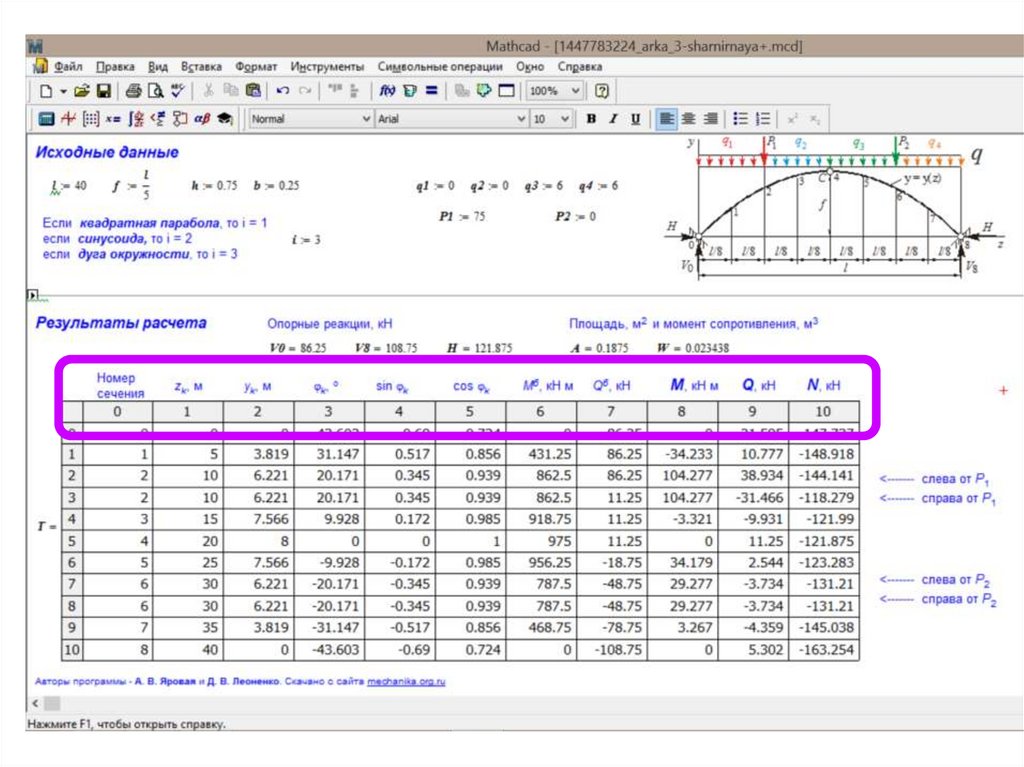
Расчеты ведем в MathCad.
Таблицу компьютерного расчета
необходимо распечатать

18.

Растянуть!!!

19.

20.

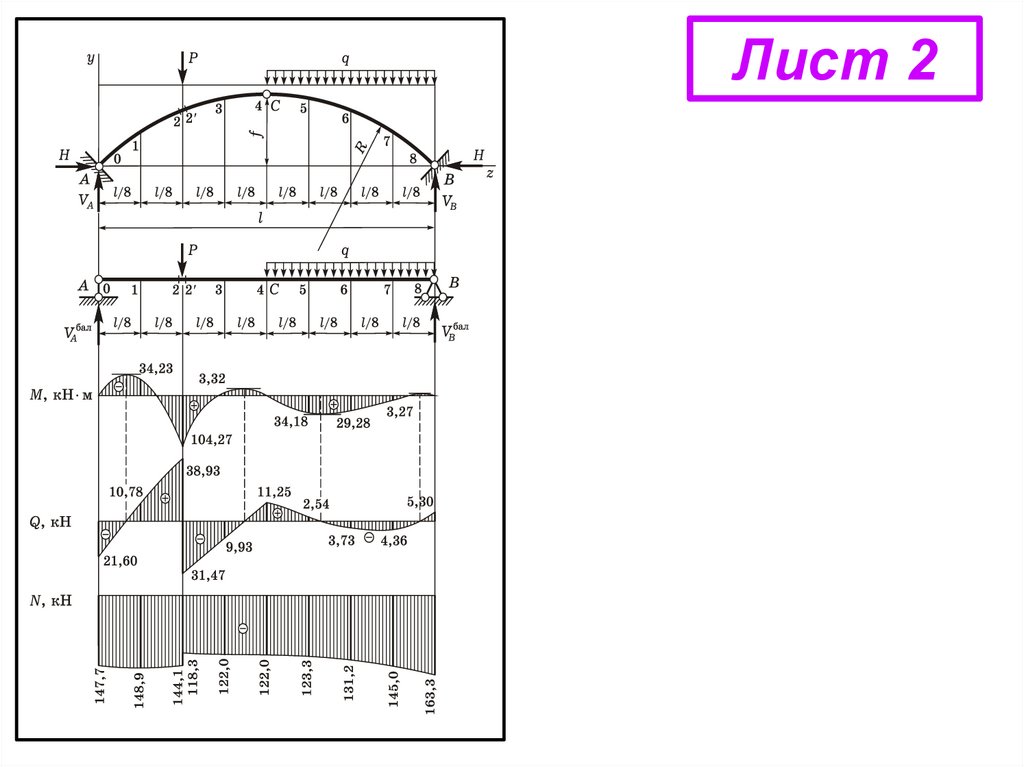
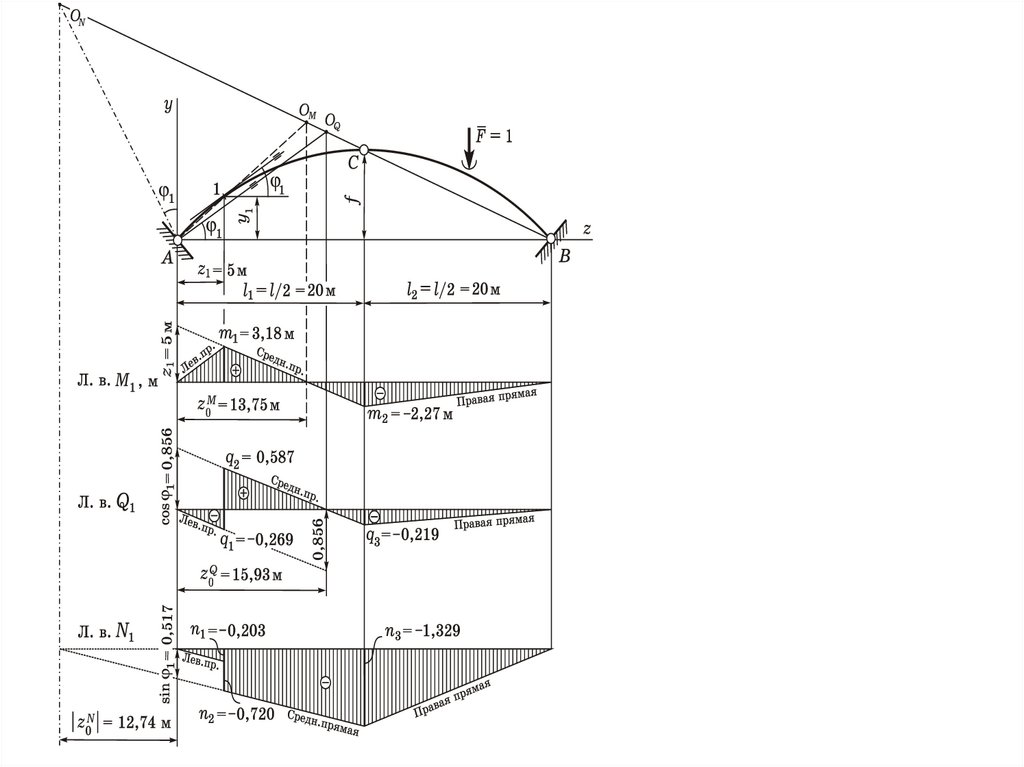
Лист 2
По полученным
данным строим
эпюры М, Q, N.
Для удобства ординаты
откладываем не от оси
арки,
а от горизонтальной базы.
Все эпюры (M, Q, N)
криволинейны!!!

21.

Вручную выполним расчет
для сечения 1.
M1
N1
Q1
M 1 M H y1 ......... кН м
Q1 Q cos 1 H sin 1 ... кН
бал
1
бал
1
N1 Q
бал
1
sin 1 H cos 1 ... кН
Результаты совпадают с данными компьютерного расчета.

22.

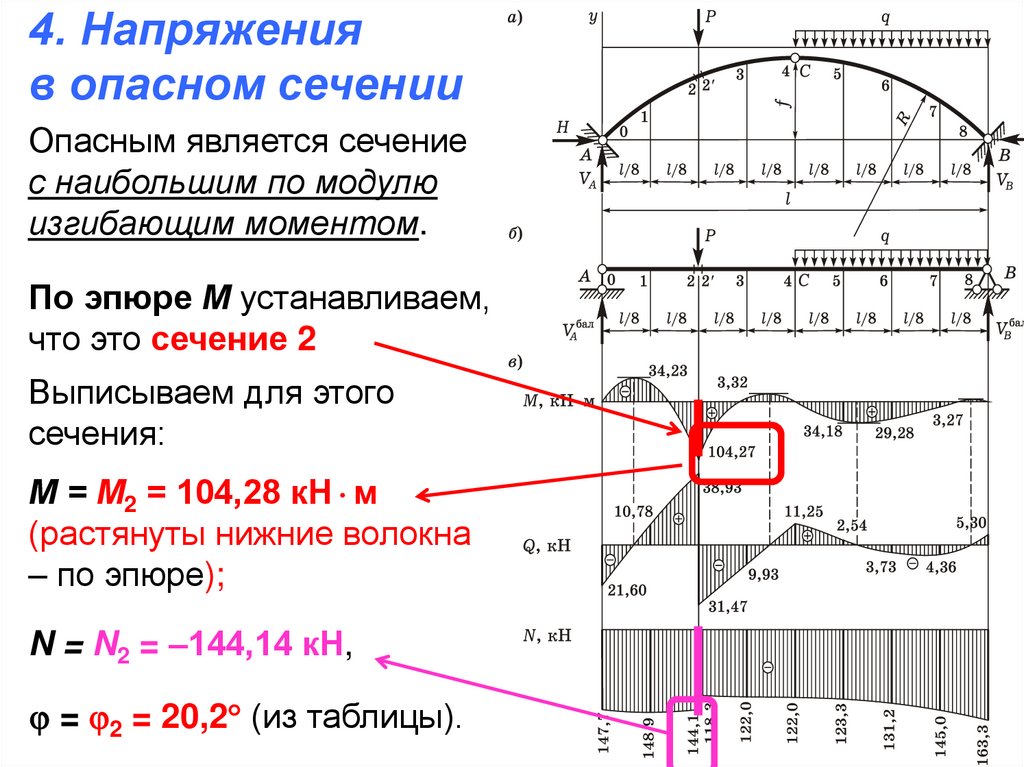
4. Напряжения
в опасном сечении
Опасным является сечение
с наибольшим по модулю
изгибающим моментом.
По эпюре М устанавливаем,
что это сечение 2
Выписываем для этого
сечения:
М = М2 = 104,28 кН м
(растянуты нижние волокна
– по эпюре);
N = N2 = –144,14 кН,
= 2 = 20,2 (из таблицы).

23.

Геометрические характеристики поперечного сечения:
2
A bh 0,1875 м
площадь
2
bh
6 3
Wx
23438 10 м
6
момент
сопротивления
Наибольшие и наименьшие нормальные напряжения:
144,14 10 104, 28 10
N M
min
6
A Wx
0,1875
23438 10
3
3
5, 22 10 Па 5, 22 МПа
6
144,14 10 104, 28 10
N M
max
6
A Wx
0,1875
23438 10
3
3,68 10 Па 3,68 МПа
6
3

24.

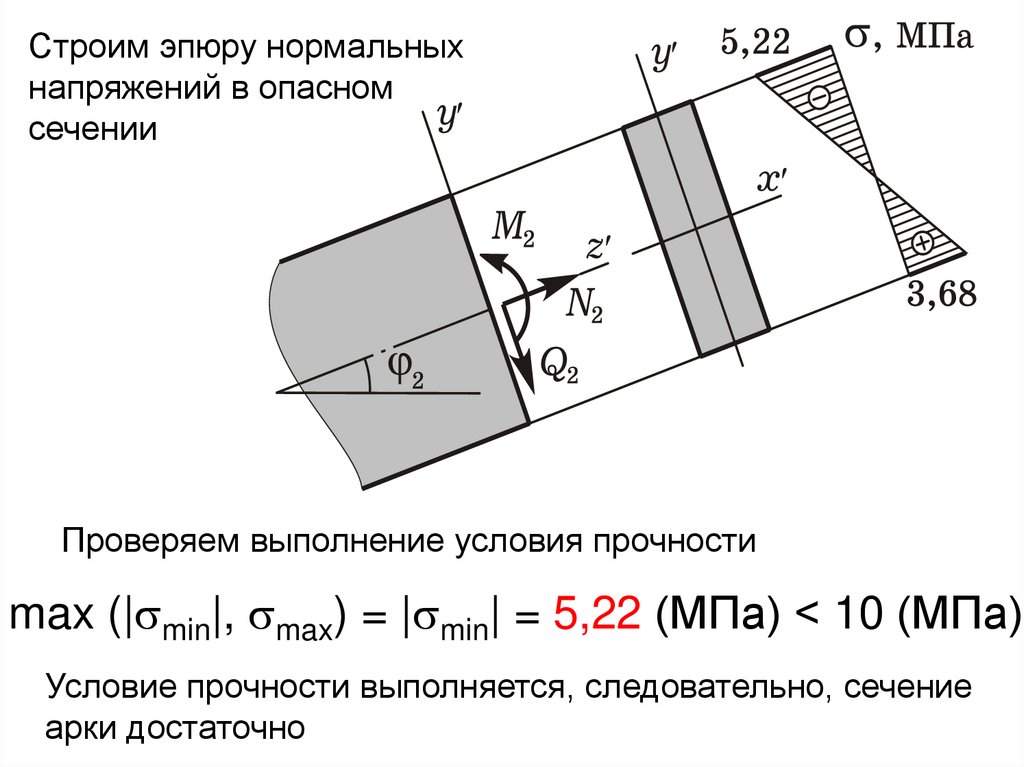
Строим эпюру нормальных
напряжений в опасном
сечении
Проверяем выполнение условия прочности
max (| min|, max) = | min| = 5,22 (МПа) < 10 (МПа)
Условие прочности выполняется, следовательно, сечение
арки достаточно

25.

.
5. Построение линий влияния
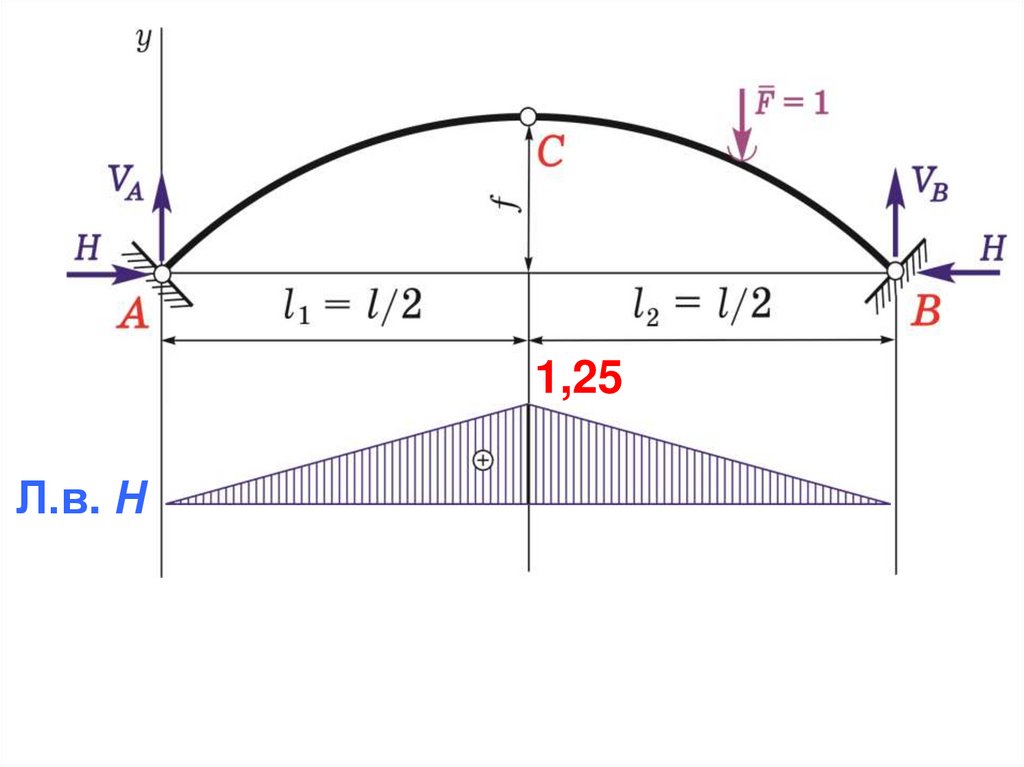
5.1. Линия влияния распора
Ордината под шарниром С
l
40
1, 25
4f 4 8

26.

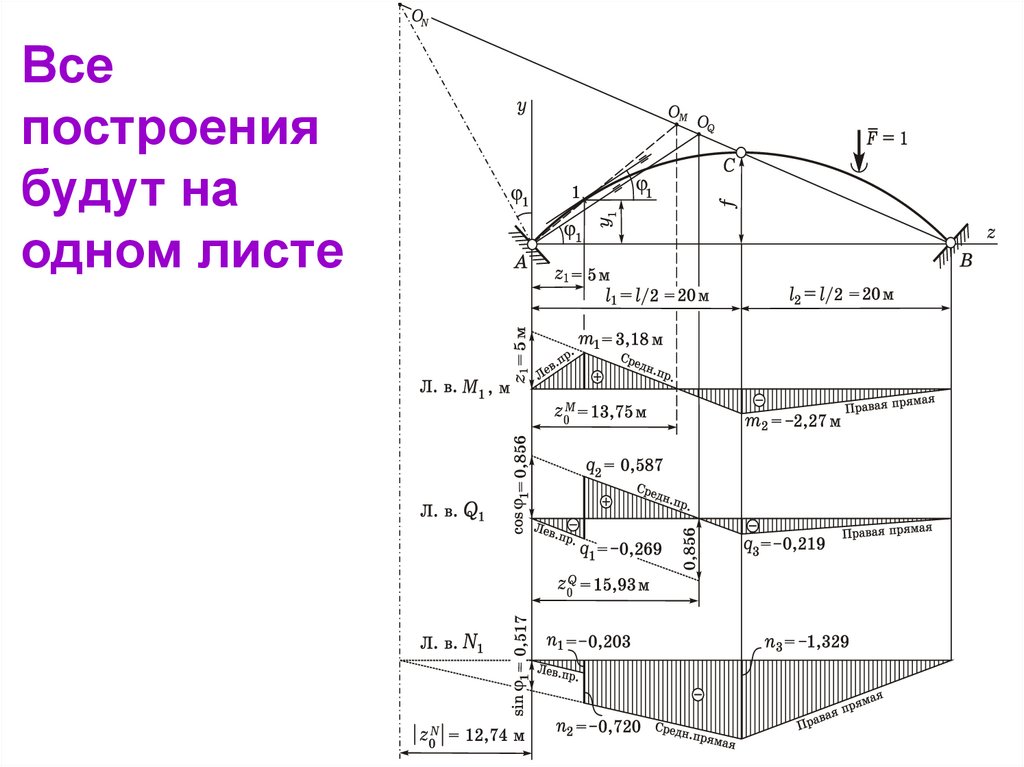
Все
построения
будут на
одном листе

27.

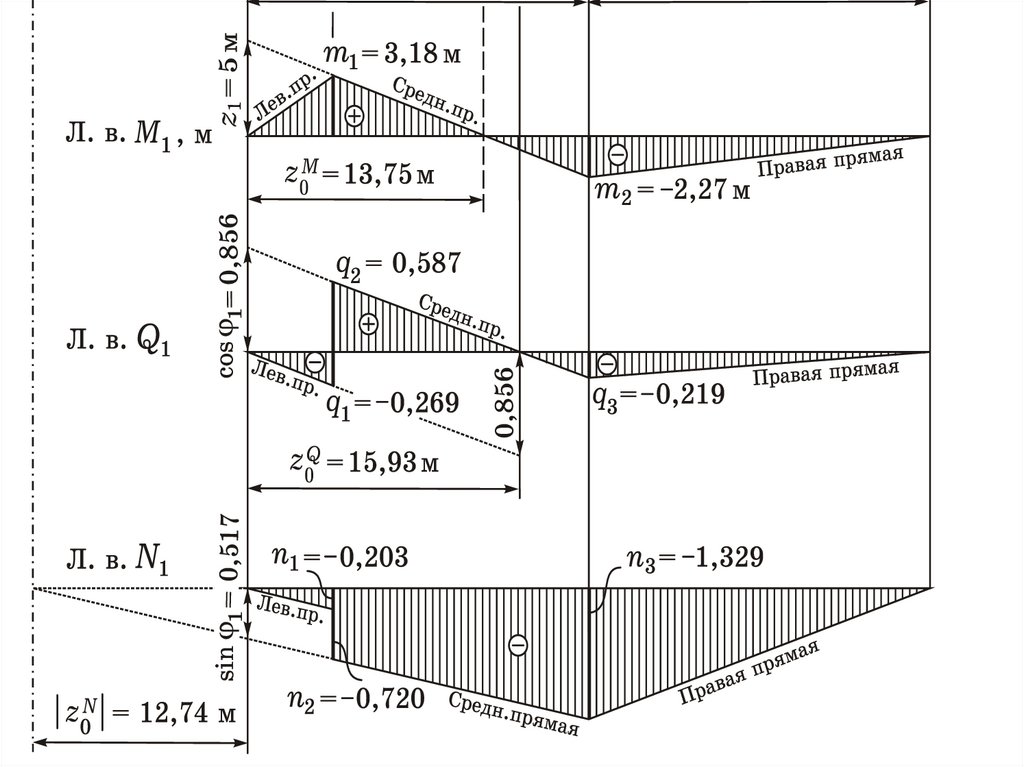
1,25
Л.в. Н

28.

5.2. Линии влияния M, Q, N в заданном сечении
По заданию сечение для построения линий влияния
k=1
(или 2, или 3)
Из таблицы выписываем его геометрические параметры
zk = z1 = 5 м,
yk = y1 = 3,819 м,
k = 1 = 31,15°
sin 1 = 0,517; cos 1 = 0,856; tg 1 = 0,604
Линии влияния внутренних усилий построим
методом нулевой точки

29.

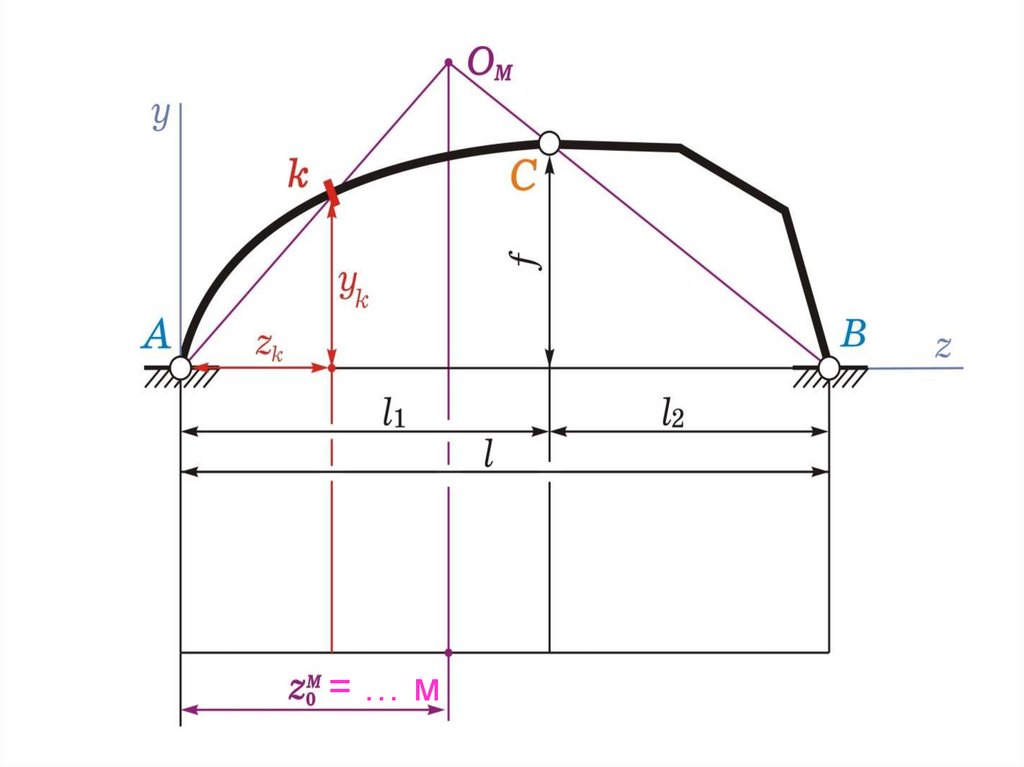
Л.в. Mk
(k = 1)
(или 2, или 3)
1) находим положение нулевой точки графически
(точку ОМ пересечения прямых Аk и ВС опустим
вниз)
и по формуле
=…м

30.

=…м

31.

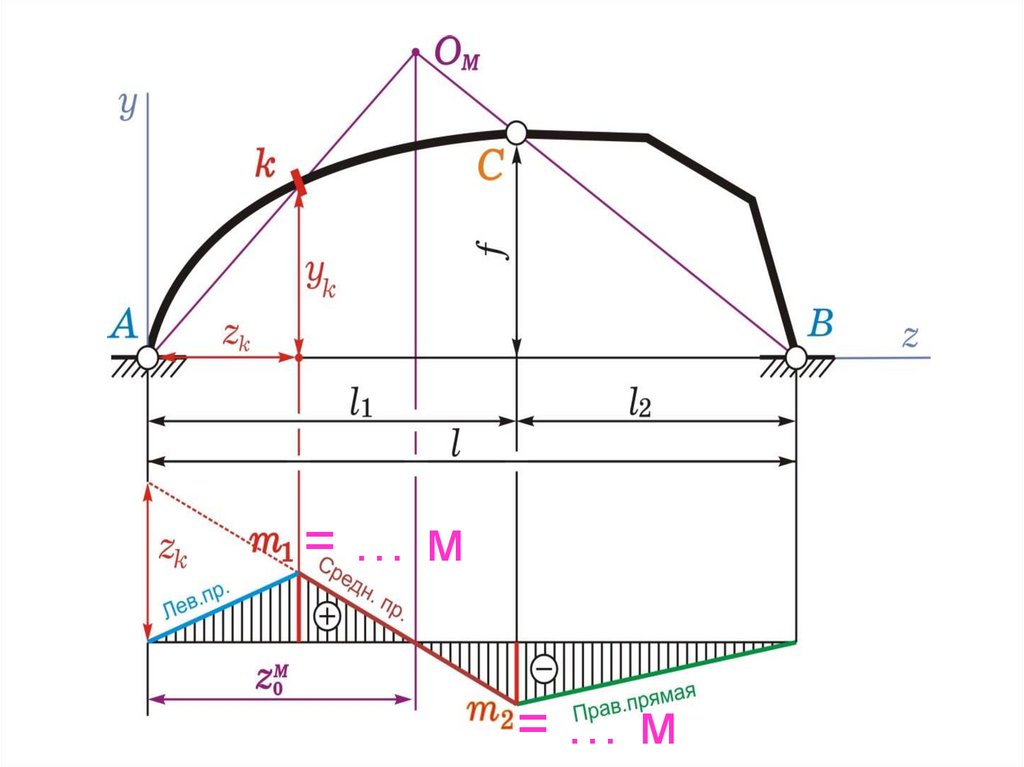
2) под т. А откладываем zK и соединяем
с нулевой точкой, получаем среднюю
прямую, справедливую на участке kС,
определяем ординаты
Обязательно
= … м указываем
эти числа на
= … м л.в.!!!
4) ординату m1 соединяем с нулем под т. А –
получаем левую прямую;
5) ординату m2 соединяем с нулем под т. В –
получаем правую прямую

32.

=…м
=…м

33.

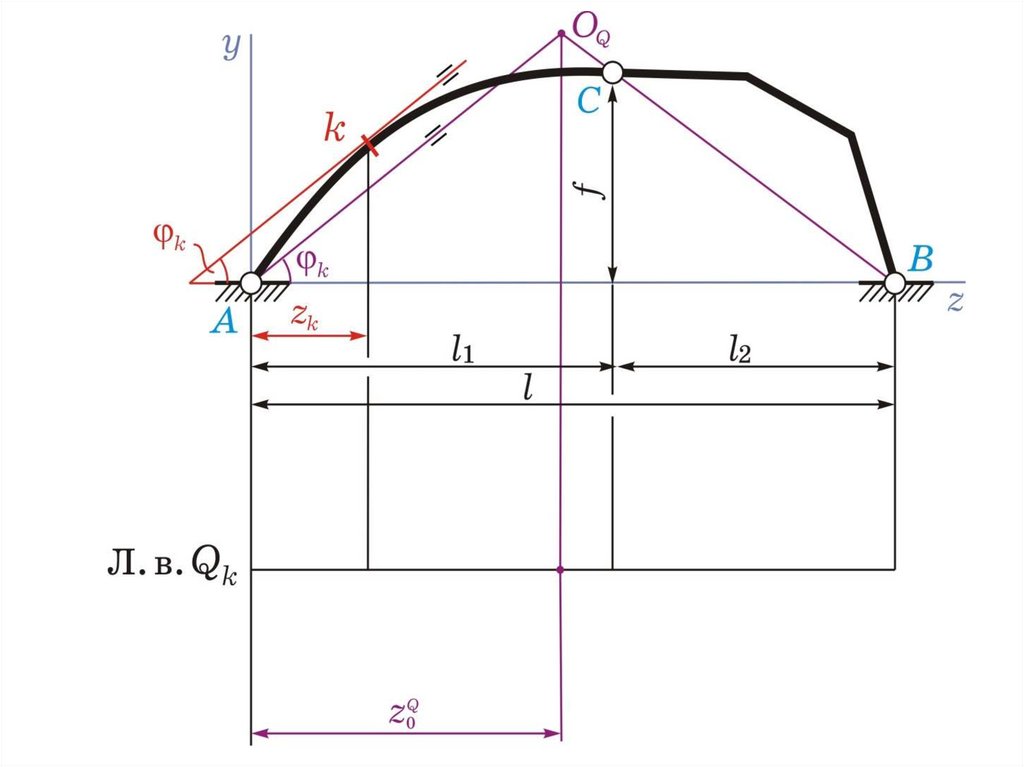
Л.в. Qk
(k = 1)
(или 2, или 3)
1) находим положение нулевой точки графически
(проведем касательную к оси арки в сечении k,
параллельно ей прямую через шарнир А до
пересечения с прямой ВС, точку их пересечения
ОQ опустим вниз)
и по формуле
=…м

34.

35.

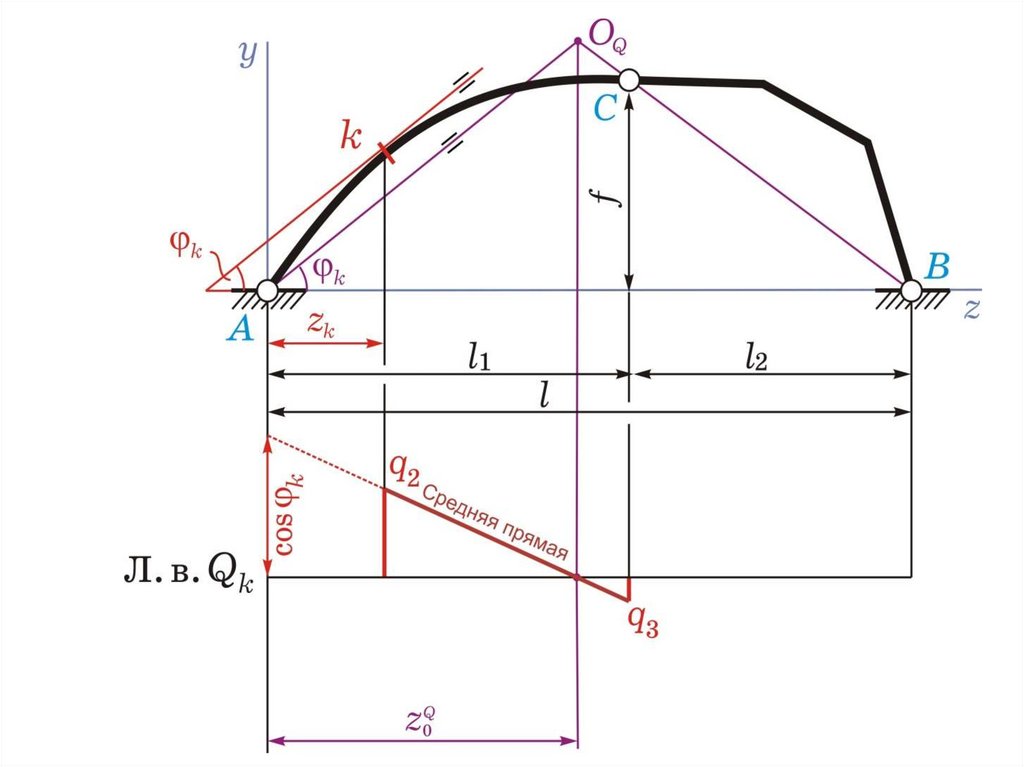
2) под т. А откладываем cos K
и соединяем с нулевой точкой, получаем
среднюю прямую, справедливую на участке kС,
определяем
ординаты
Обязательно
указываем
= … эти числа на
л.в.!!!
=…
(безразмерные)

36.

37.

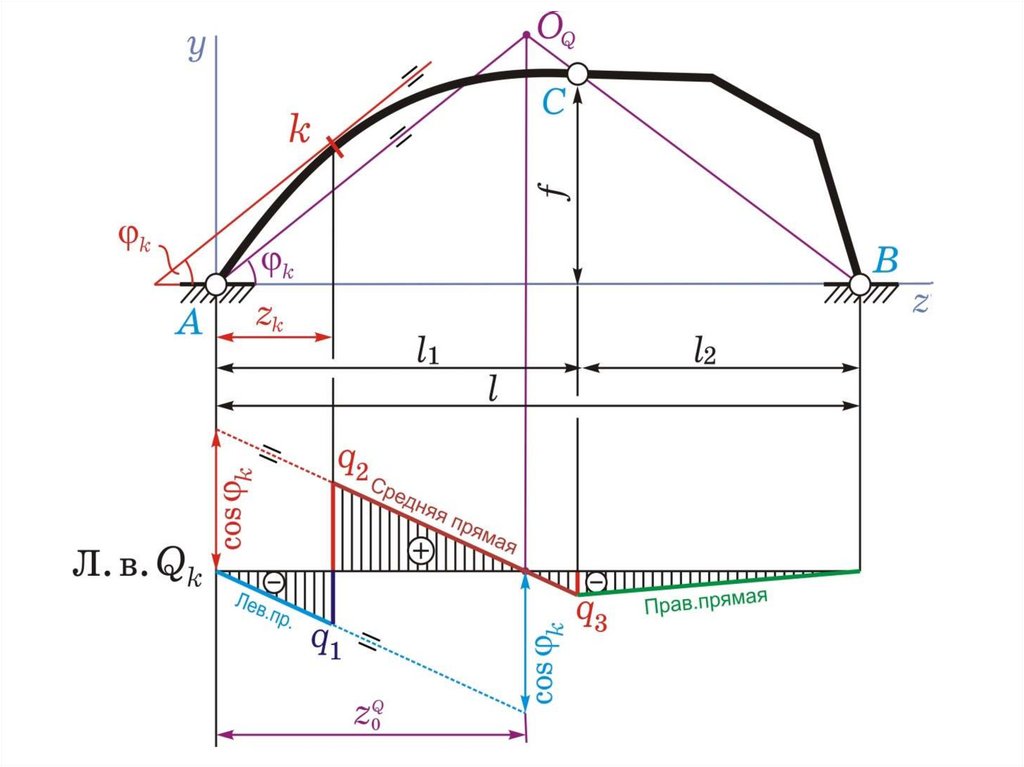
4) ординату q3 соединяем с нулем под т. В –
получаем правую прямую;
5) из нуля под т. А
параллельно средней прямой
проводим левую прямую,
определяем ординату
=…
(безразмерная)

38.

39.

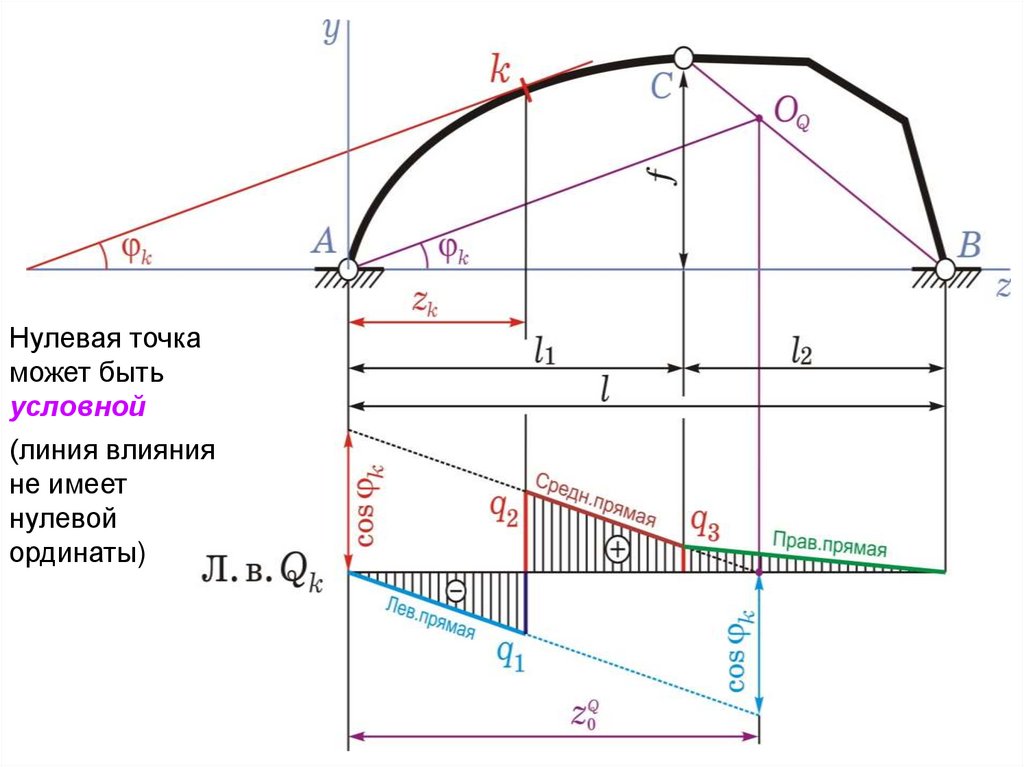
Нулевая точка
может быть
условной
(линия влияния
не имеет
нулевой
ординаты)

40.

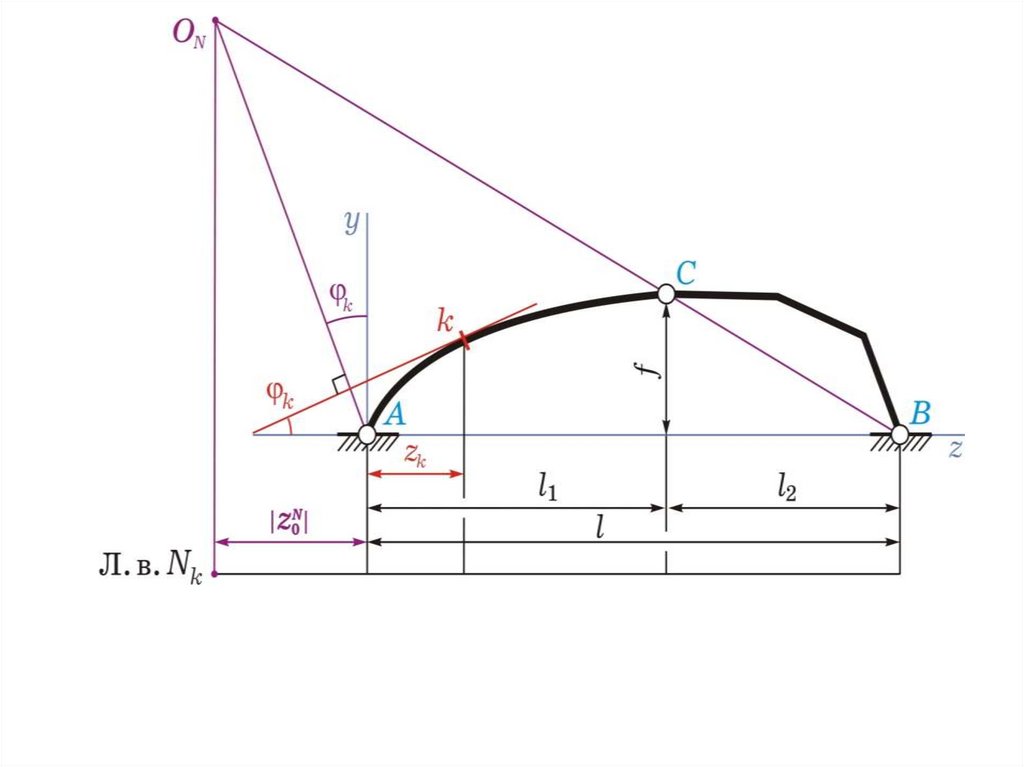
Л.в. Nk
(k = 1)
(или 2, или 3)
1) находим положение нулевой точки графически
(проведем касательную к оси арки в сечении k,
перпендикулярно ей проведем прямую через
шарнир А до пересечения с прямой ВС; точку
пересечения ОN этих прямых опустим вниз)
и по формуле
=…м

41.

42.

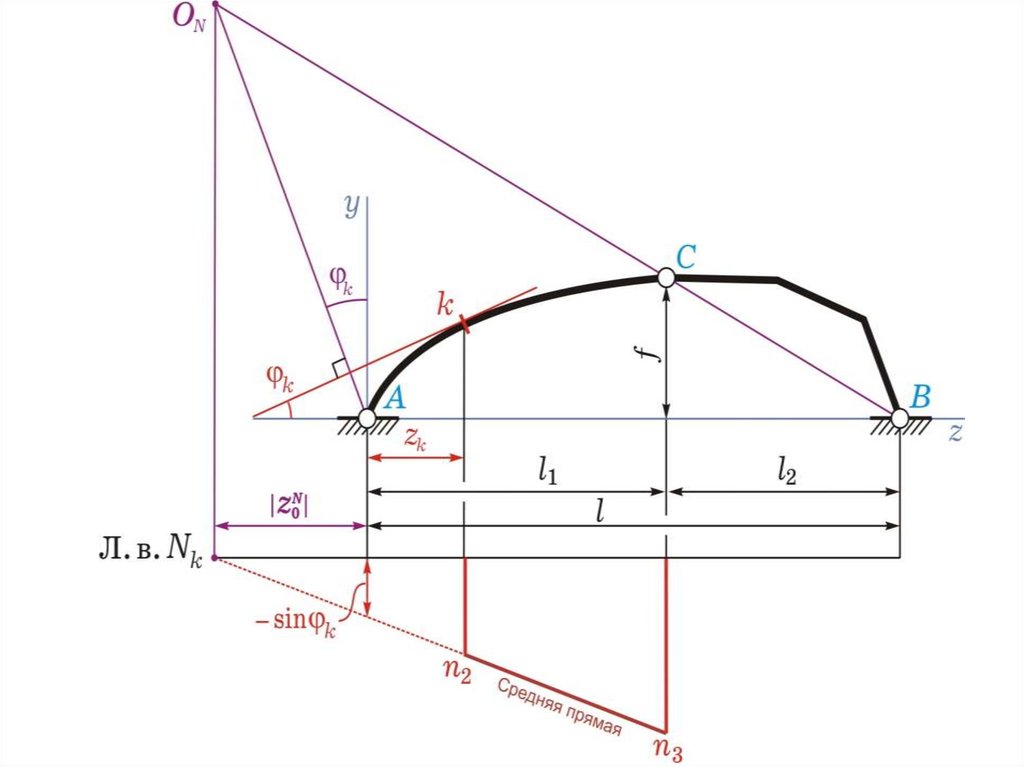
2) под т. А откладываем –sin K
и соединяем с нулевой точкой, получаем
среднюю прямую, справедливую на участке kС,
определяем ординаты
=…
=…
Обязательно
указываем эти
числа на л.в.!!!
(безразмерные)

43.

44.

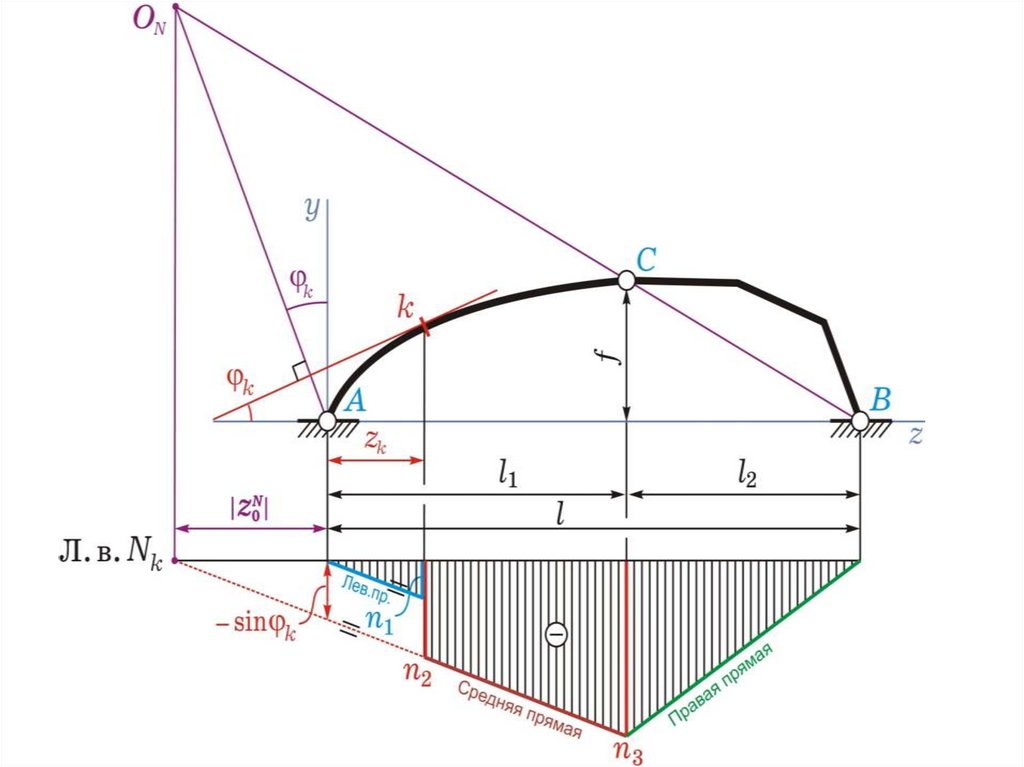
4) ординату n3 соединяем с нулем под т. В –
получаем правую прямую;
5) из нуля под т. А параллельно средней
прямой проводим левую прямую,
определяем ординату
=…
(безразмерная)
Обязательно
указываем
это число на
л.в.!!!

45.

46.

47.

48.

49.

6. Определение расчетных положений
временной нагрузки для заданного
сечения k = 1 и расчетных моментов
Так как на нормальные напряжения
наибольшее влияние оказывают
изгибающие моменты, будем
ориентироваться на л.в. Mk
Исследуем два положения нагрузки:
по положительному и отрицательному
участкам л.в.
Определим расчетные значения момента в
заданном сечении.

50.

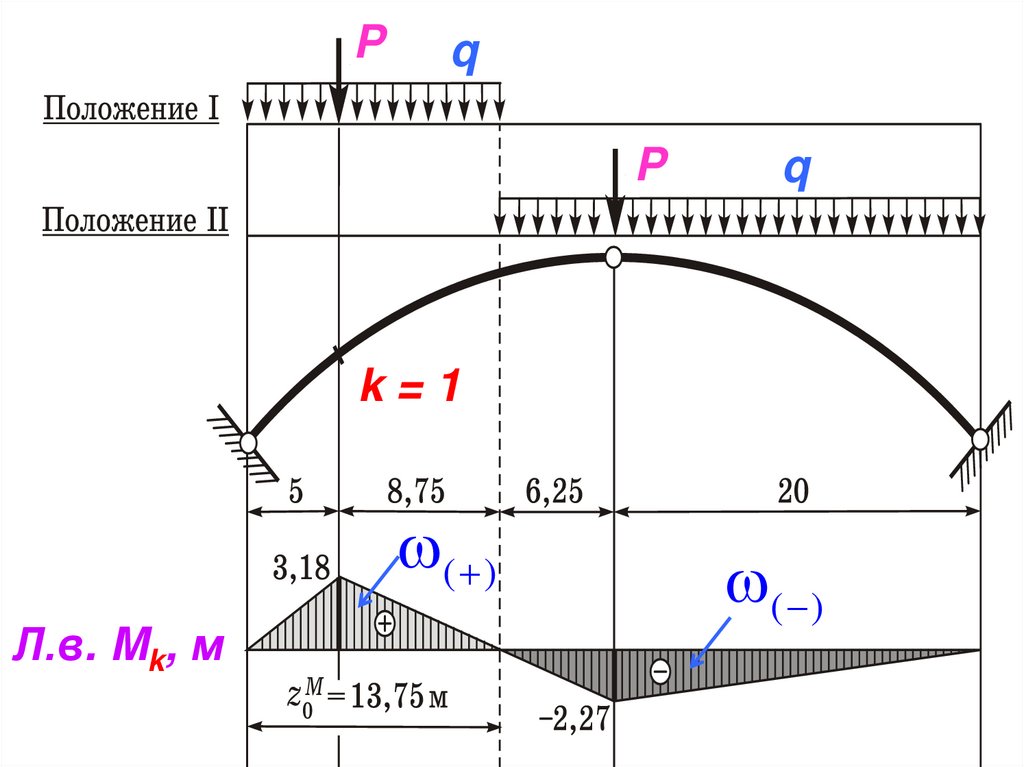
P
q
P
q
k=1
( )
Л.в. Mk, м
( )

51.

Если нагрузка в положении I, то
M P 3,18 q 3,18 13,75
( )
ордината под Р
I
k
1
2
30 3,18 3 21,86 160, 99 кН м
Если нагрузка в положении II, то
M P ( 2, 27) q 12 ( 2, 27) 26, 25
II
k
ордината под Р
( )
30 ( 2, 27) 3 29,79 157, 48 кН м

52.

M 160, 99 кН м
I
k
M 157, 48 кН м
II
k
Для прочностных расчетов необходимы
оба эти значения.