Строительная механика. Часть 2. Понятие о нелинейно деформируемых системах и методах их расчёта

1.

Строительная
механика
Часть II
ПОНЯТИЕ О НЕЛИНЕЙНО
ДЕФОРМИРУЕМЫХ
СИСТЕМАХ
И МЕТОДАХ ИХ РАСЧЁТА

2.

Нелинейно деформируемой
называется система, для которой зависимость
между параметром Р воздействия ( нагрузки )
и характерным (обобщённым) перемещением
не прямо пропорциональная.
НДС с мягкой
нелинейностью
(МН)
2
P
d P ( )
0
2
d
Р ( )
(
)
P
0
dP ( )
tg ( ) = C ( ) – обобщённая
d
жёсткость системы
НДС
P
НДС с жёсткой
с комбинированной
нелинейностью
(ЖН)
нелинейностью
2
d P ( )
0
2
d
0
ЖН
МН
0
Виды
нелинейностей:
1) физическая (ФН);
2) геометрическая (ГН);
3) конструктивная (КН).

3.

Физическая нелинейность – нелинейность зависимости Р – ,
обусловленная физико-механическими свойствами материала,
не описываемыми законом Гука.
i
σ i 1 (σ1 σ 2 )2 (σ 2 σ 3 )2 (σ 3 σ1 )2
2
i 2 ( 1 2 )2 ( 2 3 )2 ( 3 1 )2
3
Сталь
0
интенсивности
напряжений
и деформаций
Бетон, древесина
2 (1 ν)
Полимеры
i
1
В
случае
ЛНС
(
=
=
0):
=
;
(резина и т.п.)
2
3
i
1
3
i

4.

Физическая нелинейность – нелинейность зависимости Р – ,
обусловленная физико-механическими свойствами материала,
не описываемыми законом Гука.
F
i
A
l
i
0
3l
F = i A 2(1 ν) i
σ i 1 (σ1 σ 2 )2 (σ 2 σ 3 )2 (σ 3 σ1 )2
2
i 2 ( 1 2 )2 ( 2 3 )2 ( 3 1 )2
3
интенсивности
напряжений
и деформаций
2
В случае ЛНС ( 2 = 3 = 0): i = 1 ; i 3 (1 ν) 1
Расчётные модели нелинейного деформирования материалов
Степенной закон (1729)
Г.Б. Бюльфингера (1693 – 1750)
i
(1756 – 1832)
i a ki
i 0
0
k<1
i
k>1
0
Параболическая
зависимость (1831)
Ф.И. Герстнера
i
i
i
0
i
s
0
i
k=1
k=0
a = s
i a 1 i a 2 2i
i
i
Идеализированные диаграммы
i Диаграмма i Диаграмма
Прандтля
Сен-Венана
s
s
i
i
0
0
Идеальный
упругопластический
материал
Идеальный
жёсткопластический
материал
Модели с упрочнением
i
i
i
Модель А.А. Ильюшина s
s
(1958)
(1911 – 1998)
i
i
0
0
i E i (1 );
УпругоЖёстко i
пластический
пластический
i
0
материал
материал

5.

Геометрическая нелинейность – нелинейность зависимости
Р – , обусловленная большими перемещениями
и/или значительным формоизменением системы.
Сущность ГН – непропорциональность деформаций и перемещений.
zz
F
l
A
A(F) < A
ФЛ
материал:
i = E* i 0
F
ГЛ
A
Г
z
u 2 v 2 w 2
1
2
x
x
x
2
2
2
v
1
u
v
w
y
2 y
y
y
2
2
2
u
w
1
v
w
z z z
z
2
u
v
u
u
v
v
w
w
y
x x y
x y
x y
v w u u v v w w
z
x
y z
y z
y z
u w u u v v w w
z
x
x z
x z
x z
u
x
сж Н п
ат ри
ии
xx
Тензор деформаций:
yy
xx xy /2 xz /2
Te yx /2 yy xz /2
/2 /2
zz
zy
zz
zx
Линейные деформации: xy
x 1 2 ε xx 1
yz
y 1 2ε yy 1
zx
1 2ε 1
ри
и
п
ГНстяжен
ра
~0,2l
и
A(F) > A
F

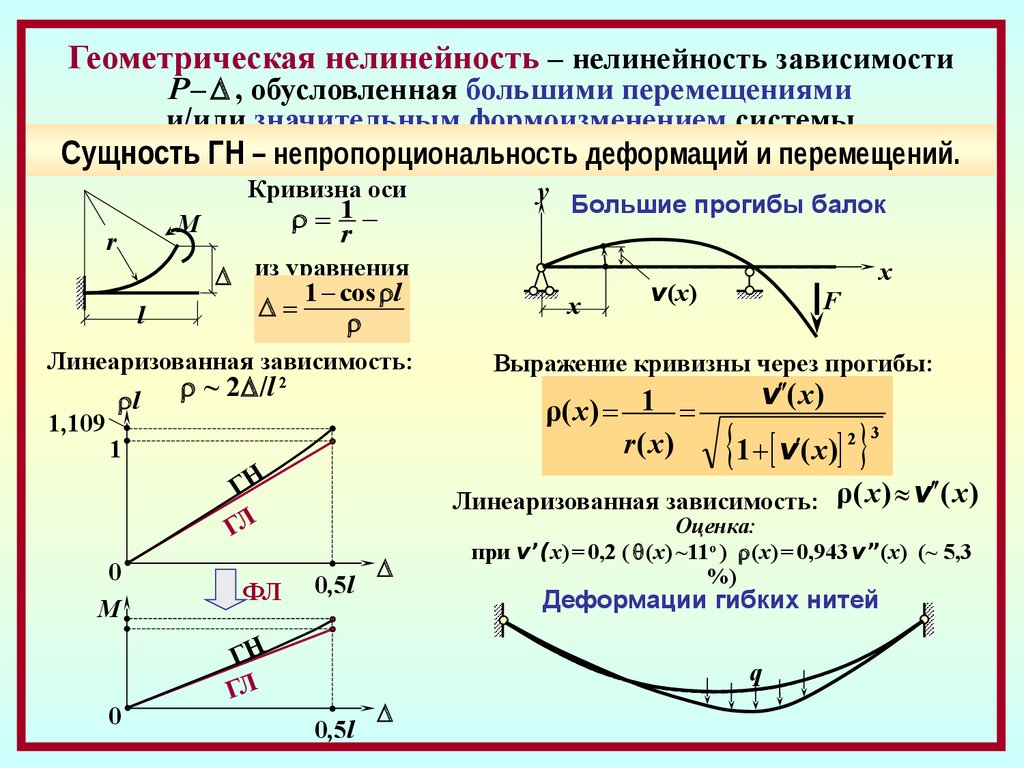
6.

Геометрическая нелинейность – нелинейность зависимости
Р – , обусловленная большими перемещениями
и/или значительным формоизменением системы.
Сущность ГН – непропорциональность деформаций и перемещений.
Кривизна оси
1
М
r
r
из уравнения
1 cos l
l
Линеаризованная зависимость:
1,109
l
~ 2 /l
2
ГН
ГЛ
0
ФЛ
Большие прогибы балок
x
x
v(x)
F
Выражение кривизны через прогибы:
ρ( x) 1
r ( x)
1
0
M
y
v ( x)
1 v ( x)
2 3
Линеаризованная зависимость: ρ( x ) v ( x )
0,5l
ГН
ГЛ
Оценка:
при v’(x) = 0,2 ( (x) ~11o ) (x) = 0,943 v”(x) (~ 5,3
%)
Деформации гибких нитей
q
0,5l

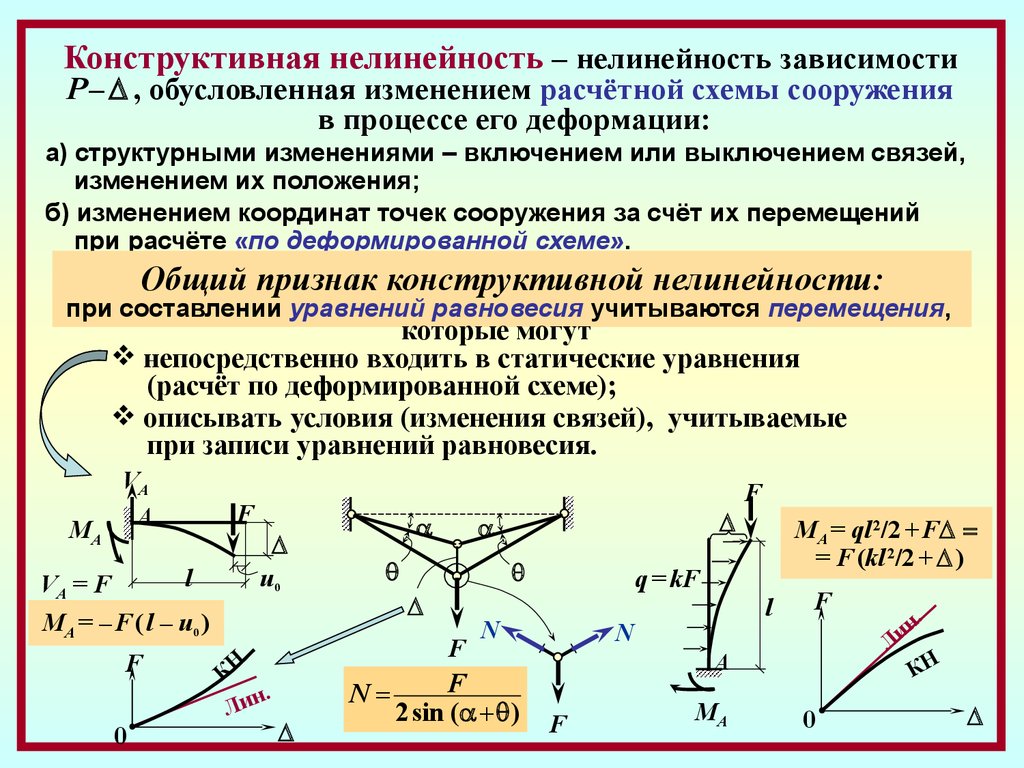
7.

Конструктивная нелинейность – нелинейность зависимости
Р – , обусловленная изменением расчётной схемы сооружения
в процессе его деформации:
а) структурными изменениями – включением или выключением связей,
изменением их положения;
б) изменением координат точек сооружения за счёт их перемещений
при расчёте «по деформированной схеме».
Общий признак конструктивной нелинейности:
при составлении уравнений равновесия учитываются перемещения,
которые могут
непосредственно входить в статические уравнения
(расчёт по деформированной схеме);
описывать условия (изменения связей), учитываемые
при записи уравнений равновесия.
VA
F
A
MA
l
VA = F
u0
F
0
КН
.
Лин
MA = – F ( l – u0 )
F
N
MA = ql 2/2 + F
= F (kl 2/2 + )
q = kF
N
F
2 sin ( )
F
l
N
F
A
F
MA
0
н.
и
Л
КН

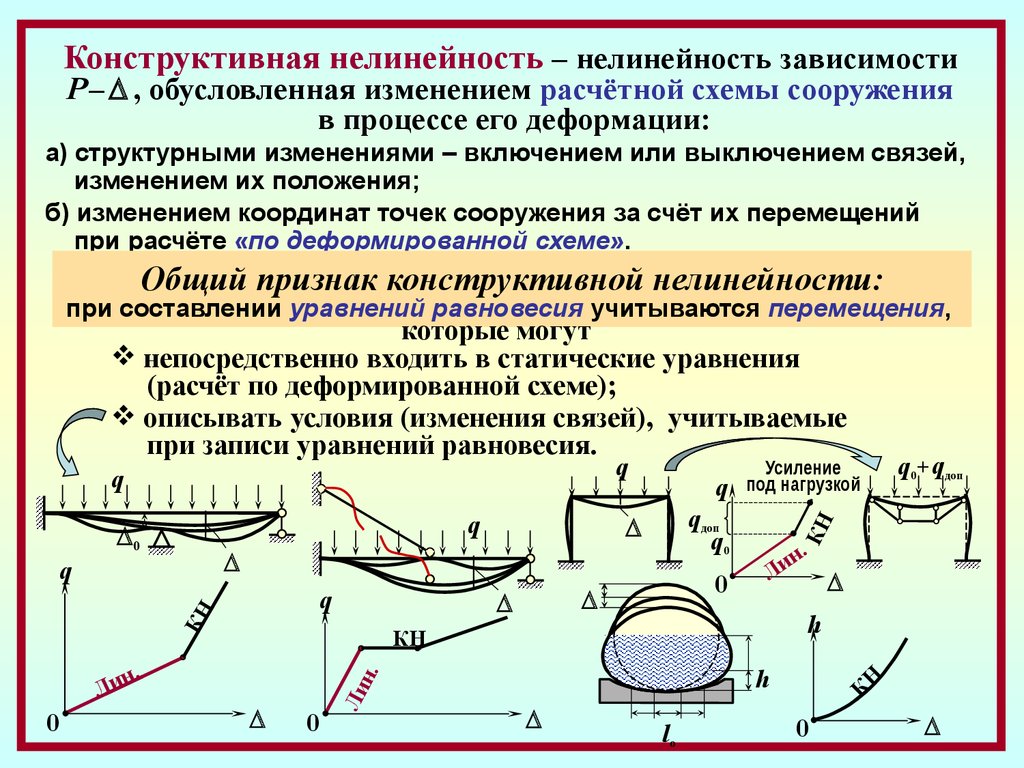
8.

Конструктивная нелинейность – нелинейность зависимости
Р – , обусловленная изменением расчётной схемы сооружения
в процессе его деформации:
а) структурными изменениями – включением или выключением связей,
изменением их положения;
б) изменением координат точек сооружения за счёт их перемещений
при расчёте «по деформированной схеме».
Общий признак конструктивной нелинейности:
при составлении уравнений равновесия учитываются перемещения,
которые могут
непосредственно входить в статические уравнения
(расчёт по деформированной схеме);
описывать условия (изменения связей), учитываемые
при записи уравнений равновесия.
q
0
q
КН
0
н
Ли
0
.
h
.
.
q0+ qдоп
h
КН
Ли
н
0
qдоп
q0
q
н
Ли
q
Усиление
под нагрузкой
КН
q
q
lо
Н
К
0

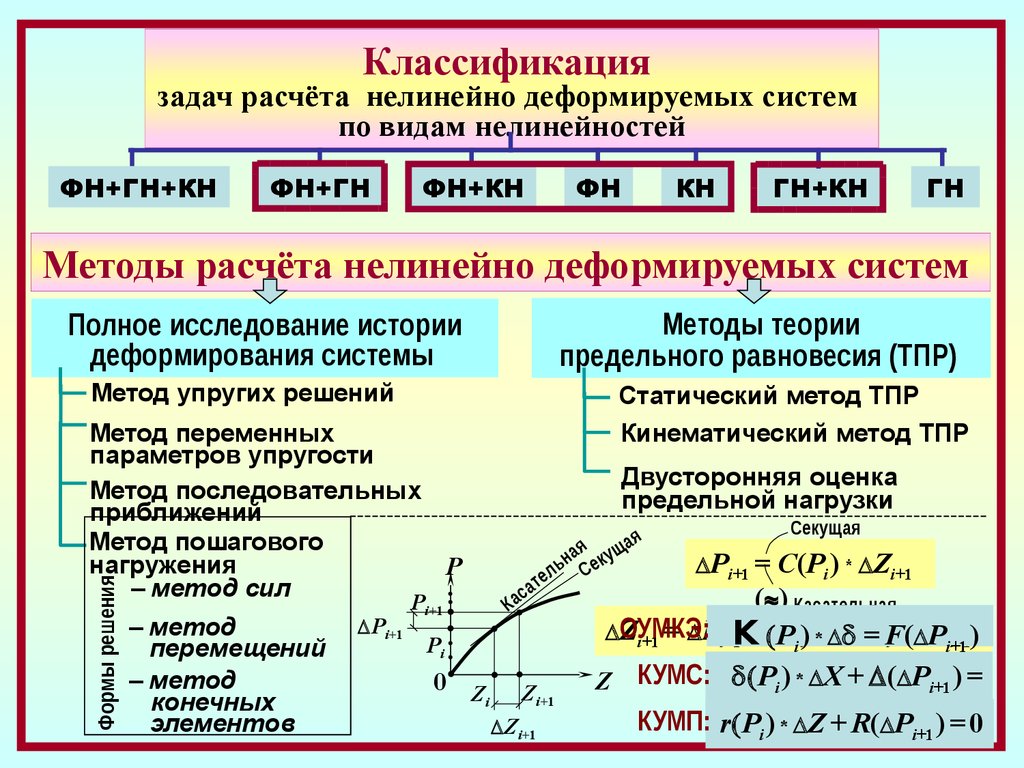
9.

Классификация
задач расчёта нелинейно деформируемых систем
по видам нелинейностей
ФН+ГН+КН
ФН+ГН
ФН+КН
ФН
КН
ГН+КН
ГН
Методы расчёта нелинейно деформируемых систем
Методы теории
предельного равновесия (ТПР)
Полное исследование истории
деформирования системы
Метод упругих решений
Формы решения
Метод переменных
параметров упругости
Метод последовательных
приближений
Метод пошагового
нагружения
P
– метод сил
P
– метод
перемещений
– метод
конечных
элементов
Pi+1
i+1
Статический метод ТПР
Кинематический метод ТПР
Двусторонняя оценка
предельной нагрузки
Ка
с
ат
я ущая
а
ьн ек
ел С
Pi
0 Z
i
Zi+1
Zi+1
Секущая
Pi+1 =
C(Pi ) * Zi+1
(~) Касательная
ОУМКЭ:
Z
P
Pi+1
K/ C(P
Pi i))*= B(P
= F(
i+1 = Pi+1
i )*
i+1)
Z КУМС: Pi ) * X + ( Pi+1 ) =
КУМП: r P ) * Z + R( P ) = 00
i
i+1

10.

Расчёт конструкций с учётом пластических деформаций
(физическая нелинейность)
Полное исследование процесса упругопластического деформирования
Системы с однородным линейным напряжённым состоянием элементов
(равномерное растяжение/сжатие, без учёта потери устойчивости при сжатии)
Статически определимая система
Статически неопределимая система
1. ССЗ: mK = 0
1. Статическая
EA
EA
сторона задачи:
q 1 l
N1 + 2N2 = 2qa
l
l K
2
N
=
2F/sin
1
F
f = l2
КЛ
f 2. Геометрическая
сторона задачи
a
a
2. ГСЗ: l2 = 2 l1
ГЛ
a
a
(совместность
перемещений
и деформаций):
3. Физическая
сторона задачи:
s
s ~ e ~ pr
в упругой
стадии < s ,
f = 2 l /sin
N
s ) = E
E EA
в стадии
0
2F
s = s /E текучести ( > s ): EA sin
= s = inv( )
F
2 l
Fu = Fs
f
Fs
sin
f При = s : 2 a
0 f
Ns = s A;
sin cos
s
4 Fa
Fs = ( s A sin )/2;
2
f = 2 a /(E sin cos ) EA sin cos
s
s
а) в упругой стадии
(при (max (j) ) < s ):
max (j) = (2) = 2 (1) ,
ССЗ
N2 = 2N1
Nl
qal
Из ФСЗ: l2 2 4
EA 5 EA
(2) = 2 (1)
N 2 4 qa .
5
qal
f 4
5 EA
Нагрузка, соответствующая пределу упругой
работы системы (при (2) = s , (1) = s /2):
A
qe 5 s , перемещение fe = s l /E
4 a
б) в упругопластической стадии
(при (2) = s , s /2 < (1) < s ; qe < q < qu ):
N2= s A; N1= 2(qa – s A) ;
f = 2 l1 = 2N1l /EA = 4l (qa – s A)/(EA)
в) в предельном равновесии ( (1)= (2)= s ):
N1= N2= s A; qu= 3/2 s A/a ; f s = 2 s l /E = 2 fe

11.

Расчёт конструкций с учётом пластических деформаций
(физическая нелинейность)
Полное исследование процесса упругопластического деформирования
Системы с однородным линейным напряжённым состоянием элементов
(равномерное растяжение/сжатие, без учёта потери устойчивости при сжатии)
Статически определимая система
Статически неопределимая система
1. ССЗ: mK = 0
1. Статическая
EA
EA
сторона задачи:
q 1 l
N1 + 2N2 = 2qa
l
l K
2
N
=
2F/sin
1
F
f = l2
КЛ
f 2. Геометрическая
сторона задачи
a
a
2. ГСЗ: l2 = 2 l1
ГЛ
a
a
(совместность
перемещений
и деформаций):
3. Физическая
сторона задачи:
s
s ~ e ~ pr
в упругой
стадии < s ,
f = 2 l /sin
N
s ) = E
E EA
в стадии
0
2F
s = s /E текучести ( > s ): EA sin
= s = inv( )
F
2 l
Fu = Fs
f
Fs
sin
f При = s : 2 a
0 f
Ns = s A;
sin cos
s
4 Fa
Fs = ( s A sin )/2;
2
f = 2 a /(E sin cos ) EA sin cos
s
s
а) в упругой стадии
4 qal
(при (max (j) ) < s ): f 5 EA
qs
qe
q
q u = qs
(2) = 2 (1)
qu 6
( 20 %)
qe 5
f
fe fs = 2fe
A
qe 5 s , перемещение fe = s l /E
4 a
б) в упругопластической стадии
(при (2) = s , s /2 < (1) < s ; qe < q < qu ):
N2= s A; N1= 2(qa – s A) ; f = 2 l1 = 2N1l /EA
f = 4l(qa – s A)/(EA)
в) в предельном равновесии ( (1)= (2)= s ):
N1= N2= s A; qu= 3/2 s A/a ; f s = 2 s l /E = 2 fe
0

12.

Расчёт конструкций с учётом пластических деформаций
(физическая нелинейность)
Полное исследование процесса упругопластического деформирования
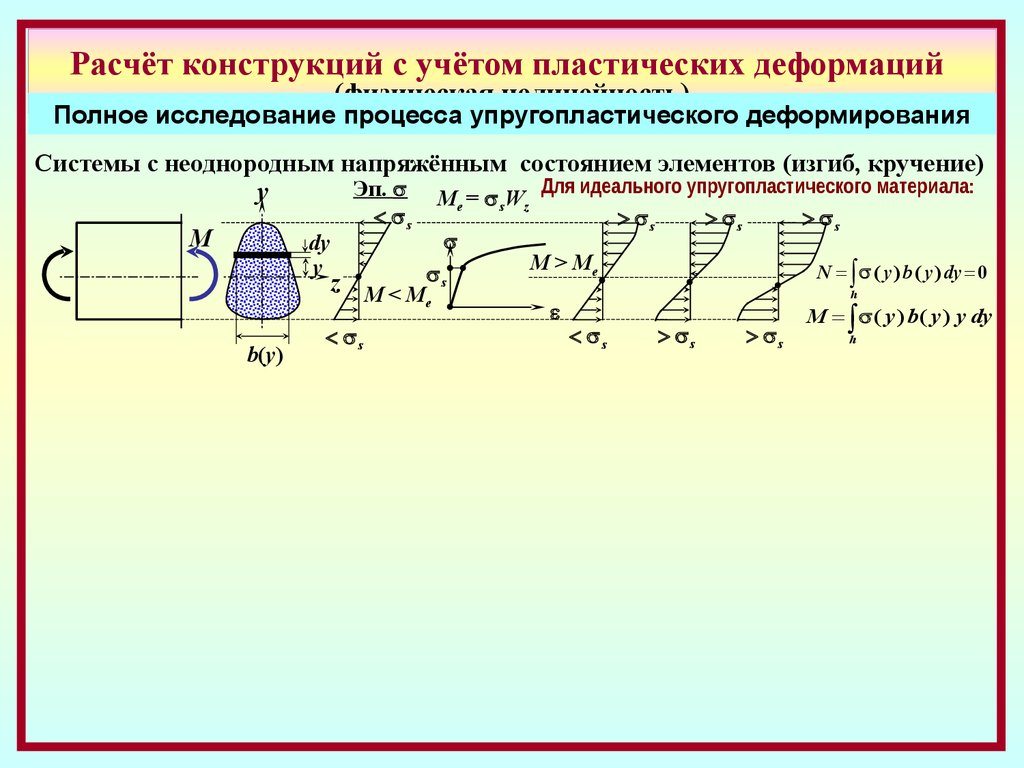
Системы с неоднородным напряжённым состоянием элементов (изгиб, кручение)
Эп. M = W Для идеального упругопластического материала:
y
e
s
z
M
dy
y
b(y)
s
s
z M<M
e
s
s
s
s
M > Me
N ( y ) b ( y ) dy 0
h
s
s
s
M ( y ) b( y ) y dy
h

13.

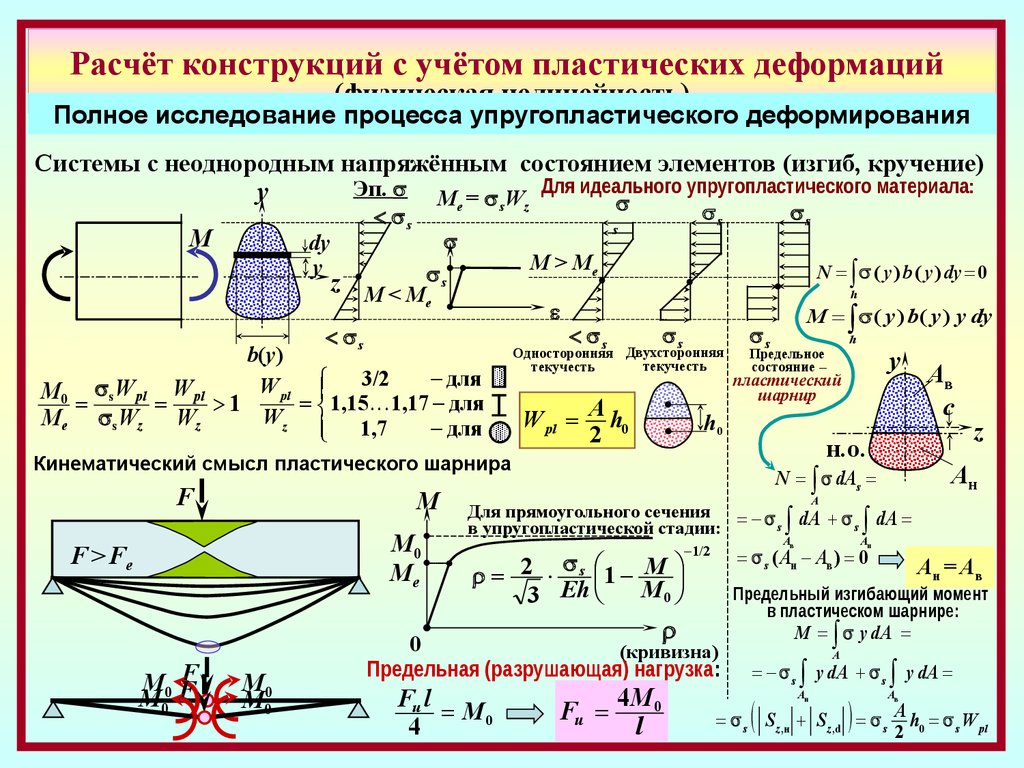
Расчёт конструкций с учётом пластических деформаций
(физическая нелинейность)
Полное исследование процесса упругопластического деформирования
Системы с неоднородным напряжённым состоянием элементов (изгиб, кручение)
Эп. M = W Для идеального упругопластического материала:
y
e
s
z
M
dy
y
s
s
s
s
M > Me
s
z M<M
e
s
b(y)
для
W pl 3/2
M0 s W pl W pl
1,15 1,17 для
1
Wz 1,7
Me s Wz Wz
для
N ( y ) b ( y ) dy 0
h
s
s
Односторонняя Двухсторонняя
текучесть
текучесть
W pl A h0
2
s
M
M0
Me
F > Fe
M
M00
y
пластический
шарнир
h0
н.о.
A
Ав
с
z
Ан
N dAs
Для прямоугольного сечения dA dA
s
s
в упругопластической стадии:
1/2
4M0
Fu
l
Aн
s ( Aн Aв ) 0
Ан = Ав
Предельный изгибающий момент
в пластическом шарнире:
0
(кривизна)
Предельная (разрушающая) нагрузка:
Fu l
M0
4
Aв
2 s 1 M
M0
3 Eh
F
M0 F
M0
h
Предельное
состояние –
Кинематический смысл пластического шарнира
F
M ( y ) b( y ) y dy
M y dA
A
s y dA s y dA
Aн
Aв
s Sz ,н S z,d s A h0 s W pl
2

14.

Расчёт конструкций с учётом пластических деформаций
(физическая нелинейность)
Теория предельного равновесия (ТПР)
Условие пластичности
(текучести) материала
Условие предельного состояния
(предельного равновесия) сечения
стержня, пластинки или оболочки
y
2
s
Жёсткопластическое
тело
3
M
N
s
При М = 0: N = N0 = s A
При N = 0: M = M0 = sWpl
При – N0 < N < N0 и – M0 < M < M0
M
m
для прямоугольного сечения:
1M0
2
Интенсивности
напряжений и деформаций
σ i 1 (σ1 σ 2 )2 (σ 2 σ 3 )2 (σ 3 σ1 )2
2
i 2 ( 1 2 )2 ( 2 3 )2 ( 3 1 )2
3
i
s
i
0
2
Условие
Мизеса – Губера – Генки
i – s = 0
Условие Треска – Сен-Венана
max ( | k | , | k – j | ) – s = 0,
k, j = 1, 2, 3
н.о.
z
s
s
M N 1 0
–1
M0 N 0
– N0
2
2
или m n 1 0
s 1
0
s
f ( , s ) = 0
m = M/M0 ; n = N/N0
Обобщённо:
Для стержней:
0
1
N0
– 10
–M
Ф ( S, S0 ) = 0
S = { Mz My Mt Qy Qz N }
Для пластин и оболочек:
S = { Mx My Mxy Qzx Qzy Txy Nx Ny }
n
N

15.

Расчёт конструкций с учётом пластических деформаций
(физическая нелинейность)
Теория предельного равновесия (ТПР)
Статический метод ТПР Кинематический метод ТПР Двухсторонняя оценка
предельной нагрузки
Статическая теорема ТПР
Кинематическая теорема ТПР
Предельная нагрузка Pu не ниже той,
которую может уравновесить статически
допустимое поле напряжений (усилий):
Pu P ( *) или Pu P (S *)
Предельная нагрузка Pu не выше той,
которая соответствует кинематически
допустимому полю скоростей
перемещений и деформаций:
Pu P ( *)
P ( *), P (S *) – нагрузка, находящаяся
в равновесии со статически допустимыми
P ( *) – нагрузка, найденная для некоторой
напряжениями (усилиями)
схемы механизма разрушения с кинематиСтатически допустимым называется
чески допустимым полем перемещений
статически возможное распределение
(деформаций)
(поле) напряжений (усилий), удовлетворяющее по всему объёму системы
Кинематически допустимым
условию f ( , s) 0 или Ф ( S , S s ) 0.
называется распределение (поле) скоростей
Статически возможным называется распре- перемещений и деформаций, удовлетворяюделение (поле) напряжений (усилий), удовле- щее уравнениям совместности и кинематитворяющее при заданных воздействиях урав- ческим граничным условиям.
нениям равновесия и статическим граничным
условиям.
Обобщающая (двойственная) теорема ТПР
Предельная нагрузка является максимальной из всех уравновешиваемых статически
допустимыми полями напряжений (усилий) и одновременно минимальной из всех нагрузок,
соответствующих кинематически допустимым полям скоростей перемещений и деформаций:
Pu sup P ( *) inf
P ( *)

16.

Расчёт конструкций с учётом пластических деформаций
(физическая нелинейность)
Теория предельного равновесия (ТПР)
Вариационные принципы статики жёсткопластических систем
Принцип минимума полной энергии системы:
из всех кинематически допустимых полей скоростей перемещений (деформаций)
истинным при заданных воздействиях является то, которому соответствует
минимальная и равная нулю полная энергия жёсткопластической системы:
П Wint W F min 0 ,
ε
(I)
Wint = D – энергия диссипации в пластических зонах (для системы
с введёнными шарнирами текучести D = –WS0 ; WS0 – работа
предельных усилий на перемещениях механизма разрушения);
WF – потенциал нагрузки ( < 0 ).
( I*)
Вариант записи ( I ): П W S 0 W F* 0 ,
WF* WF – работа нагрузки на перемещениях предельного
пластического механизма.
Принцип максимума работы нагрузки:
из всех статически допустимых полей напряжений истинным является то,
которому соответствует максимум работы нагрузки, уравновешиваемой
этим полем, на истинных перемещениях механизма разрушения:
P P max
S
или
(P P ) 0
( II )

17.

Расчёт конструкций с учётом пластических деформаций
q
(физическая нелинейность)
Определение предельных нагрузок балок
1. Решение статическим методом ТПР
R
Сечение – постоянное
l
ql 2/8
M (x0)
Определение статически возможного поля изгибающих моментов:
x
x0
– дифференциальное уравнение равновесия: d 2M (x) /dx2 = – q = const,
его решение: M (x) = – qx2/2 + C1x + C2 ;
– статические граничные условия: M (0) = 0, Q(0) = – dM/dx(0) = – R
C2= 0, C1= R .
M (x) = – qx2/2 + Rx
– – параметр варьирования статически возможного поля моментов,
тогда M (l) = – ql 2/8 R = ql (1 – /4)/2 , x0 = R/q = l (1 – /4)/2
qx ql 2 x
M ( x) x R
4 1 x
2 8 l
l
Условия допустимости статически возможного поля:
q ( q * 1
I
M (l ) M 0
8M 0
M (x ) M
1
,
где
q*
qII ( q *
2
0
0
2
l
1
qII ( )
4
x
По статической теореме ТПР : qu max q ( ) u
x
x
α
x
x
x
qI ( ) qI ( u) = qII ( u)
2
u 24 u 16 0
q
max
q
( )
Область статически
1
1
u
α
допустимых значений q ( )
u(1, 2) 12 8 2
u 2
M0
q*
u
1/2
1/4
3/4 1 5/4 3/2
11,66
1
u
4 u 12 8 2 0,6863
l2
u
0
x
5
4
3
2
1
x
q ( ) ( * q* )
ql 2
M0
82
2
ql
1 M0
8
4

18.

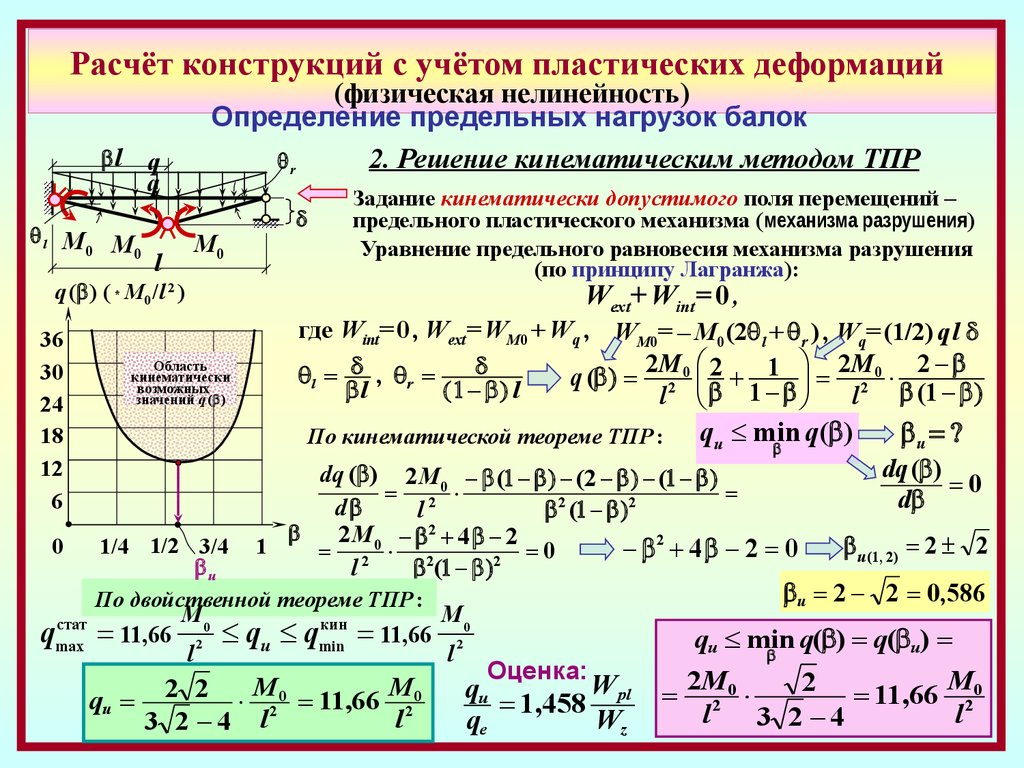
Расчёт конструкций с учётом пластических деформаций
l
(физическая нелинейность)
Определение предельных нагрузок балок
2. Решение кинематическим методом ТПР
r
q
q
l М М
0
0
М0
l
q ( ) ( * M0 /l 2 )
36
30
24
18
12
6
0
Задание кинематически допустимого поля перемещений –
предельного пластического механизма (механизма разрушения)
Уравнение предельного равновесия механизма разрушения
(по принципу Лагранжа):
Wext+ Wint= 0 ,
Область
кинематически
возможных
значений q ( )
где Wint= 0 , Wext= WM0 + Wq , WM0= – M0 (2 l + r ) , Wq= (1/2) q l
2M 0 2
1 2M0 2
l , r
q
(
2
l
l
l 1
l 2 (1
По кинематической теореме ТПР :
qu min
q( )
u
dq ( )
dq ( ) 2 M 0 ( (2 (
0
2
2
2
d
d
l
(
2
2M 4 2
2
1/4 1/2 3/4 1
u (1, 2) 2 2
4 2 0
20 2
0
2
u
l
(
u 2 2 0,586
По двойственной теореме ТПР :
стат
qmax
11,66
M0
l
2
кин
qu qmin
11,66
M
M
qu 2 2 20 11,66 20
l
3 2 4 l
M0
l
qu min
q( ) q( u)
2
Оценка:
W
qu
1,458 pl
qe
Wz
2M 0
2 11,66 M0
2
l
l2
3 2 4

19.

Расчёт конструкций с учётом пластических деформаций
(физическая нелинейность)
Определение предельных нагрузок балок
1. Решение статическим методом ТПР
F
M0
Сечение – постоянное
3 Fl
16
M max
l/2
l/2
*
F(1)
В упругой
стадии
М0
4M0
l
*
F(2)
2M0
l
Fl/4
Fl/4
*
F(3)
6M0
l
Статически допустимые поля изгибающих моментов
5 Fl
32
3
Fl M e s Wz
16
W
Fe 16 s z
3
l
М0
Fl/4
M0
M0
Статически невозможное
поле моментов
Статически недопустимое
поле моментов
M0
2. Решение кинематическим методом ТПР
F
М0
Кинематически недопустимое
поле перемещений
F
l/4
М0
М0
F
М0
WF WM 0 0
F /(l/2)
F* F – M0* ( 2*2 + ) = 0
F(1)
10 M0
l
М0
Fu
F
М0
М0
F* F – M0* 3 = 0
F(1)
6 M0
l

20.

Расчёт конструкций с учётом пластических деформаций
(физическая нелинейность)
Определение предельных нагрузок балок
Балки переменного сечения
Способ выравнивания моментов
F1
l1
M0
M0
q2
l2
qj
lj
Fn – 1 Fn(1) Fn(2)
ln – 1
ln
M0
Эпюра
предельных
моментов
сечений
a
M0
c
b
Статически
допустимое поле
определяется
точками a, b, c
Подбор сечений балки по предельному равновесию
F = 20 кН
q
=
50
кН/м
l = 6 м ; s = 240 МПа
а) при независимых нагрузках –
определение предельных нагрузок
Сечение по М01:
А
В
в каждом пролёте отдельно:
Wpl (1) = M01/ s =
l
l/2
l/2
F1, u , q2, u , qj, u , …, Fn, u
= 469 см3
Любая статически возможная
эпюра моментов
№ 27а
б) при однопараметрических нагрузках M
2
ql /8 +Fl/4=
MАА = 112,5 = M
MBB
F1 = 1P, q2 = 2 P, qj = j P, …, Fn = n P :
= 255M
кН
*м Сечение по М02:
02
Wpl(2) = M02/ s =
M01
Pu = min Pj, u
M02
112,5
= 831 см3
2
ql /8 = 225 кН*м
199,52
№ 36

21.

Расчёт конструкций с учётом пластических деформаций
Сечения
одинаковые
l /2 l /2
4F
2
4
(физическая нелинейность)
Предельное равновесие рам
nst = 1 1. Решение статическим методом ТПР
l /2 2F 1 3
(из x = 0)
l /2 А 2F– Х В Х
3F
F
(из m = 0) (из m = 0)
B
A
X – характеристика
статически возможного
поля усилий
F* ( * M0 /l )
3
2
1
N варианта
(i)
1
2
3
4
5
6
Значение
характеристики X(i)
0
1F
2
5F
8
3F
4
7F
8
F
Статически
возможное
поле усилий
( эпюра
изгибающих
моментов,
соответствующих X(i) )
Условие
допустимости статически
возможного
поля усилий
Значение
параметра
нагрузки
1
2
1
1/2
1/2
1
3/2
1/2
3/8
3/8
1
3/4
1/4
7/8
11/16
3/4
1/4
5/8
1
7/8
3/4
5/8
7/8
1/8
5/8
9/16
3/4
5/8
1
1/2
1/2
Все ординаты умножать на Fl
M max
M max
M max
M 3 M 0 M M M3 M0
3
0
M 3 3 Fl M 3 Fl M 3 7 Fl
2
8
M
*
F(1)
2 0
3 l
*
F(2)
M0
l
M max M 3
M4 M0
M 3 3 Fl
4
M max
M max
M4 M0 M M
4
0
M 4 Fl
M 3 7 Fl
8
M
M
M
*
*
*
F(3)
8 0 F(4)
4 0 F(5)
8 0
7 l
3 l
7 l
*
F(6)
M0
l
По статической теореме ТПР:
0
1 5 3 7 1
2 8 4 8
X/F*
*
*
4 M0
Fu max
F
(
X
)
max
F
F
(i )
(4)
X
3 l
M
Fu 4 0
3 l

22.

Расчёт конструкций с учётом пластических деформаций
l /2 l /2
4F
2
(физическая нелинейность)
Предельное равновесие рам
2. Решение кинематическим методом ТПР
4
Количество возможных вариантов механизмов разрушения – nm Сk
где r – число пластических шарниров в механизме ( r = nst + 1 );
k – число сечений, в которых могут образовываться шарниры.
3
l /2 2F 1
l /2 А nst = 1 В
r = 1 + 1 = 2; k = 4
r
k!
,
r! (k r )!
nm= 4!/(2!*2!) = 6
N варианта
(i)
1
2
3
4
5
6
Комбинация
сечений с
пласт.шарн.
1 2
1 3
1 4
2 3
2 4
3 4
Схема
предельного
механизма,
соответствующего i-му
кинематически допустимому полю
перемещений
M0
2F
2F
M0
Уравнение
возможных
работ
WF* WM 0
2F l
2
M
(
0
0
0
Значение
параметра
нагрузки
4F
3
4F
F(1) 3
M0
l
M0
M0
4F
2F
3
2F l 4F l
2
3 2
M0 ( 0
3 3 3
F(2) 6
M0
l
По кинематической теореме ТПР:
M
Fu min F(i) F(6) 4 0
3 l
M0
4F
4F
M0 M0
2F
M0
2 2F
2F l
2
M0 ( 0
2
M
F(3) 3 0
2 l
2F l 4F l
2
2
M0( 0
F(4) 4
4F
M0
M0
l
M0
2F
2F l
2
M0( 0
F(5) 2
M0
l
M0
M0
2F l 4F l
2
2
M0( 0
M
F(6) 4 0
3 l
теореме ТПР:
M0 По двойственной
4
4 M0
*
Fu
F
max
F
F
min
F
u
(i )
u
(i )
3 l
3 l

23.

Расчёт конструкций с учётом пластических деформаций
(физическая нелинейность)
Предельное равновесие пластин
s
M
s
M h
M
s
s
Погонный предельный момент: M = h2/4
0
s
Na
M0= Na h0 =
= s,a Aa h0
h0
Условие предельного состояния сечения пластины: m x m y kt m xy 1 0
(mx= Mx /M0 ; my= My /M0 ; mxy= Mxy /M0 ; kt = 3 v 4 )
2
2
2
Типовые схемы предельных пластических механизмов пластин
Вид
нагрузки
Сосредоточенная
Распределённая
Типы пластин по очертанию контура
Круглые
Прямоугольные
Полигональные
Эллиптические

24.

Расчёт конструкций с учётом пластических деформаций
(физическая нелинейность)
Предельное равновесие пластин
Определение предельной нагрузки ( параметра Pu ) пластин
кинематическим методом ТПР
Уравнение баланса работы нагрузки
*
*
W
F D где WF P P ; D M0 M0
и энергии диссипации в пластических шарнирах:
– перемещение точки приложения сосредоточенной нагрузки P,
P P
D = D к + Dв
эпюры перемещений предельного механизма
V – объём
при равномерно распределённой нагрузке q
По кинематической теореме ТПР:
Pu P D M0 M0
P
P
контурных
внутренних
шарниров текучести
Прямоугольные пластины при равномерно распределённой нагрузке q
внутр
M0 конт
q V 1 ab
b
M 0 M0
3
к1
d
к1 2
a
к2 2
b
к2
к2
2
1
в
конт
M 0 к1 b nb к2 a na
2 d a sin tg na , nb – количества защемлённых сторон
d
длинами a и b соответственно
1
1
a
2
1
a sin 2 sin 2
2
a/(2sin )
a cos cos cos
2
2 sin
2
a
в
l
diag
sin
cos2 a sin tg a cos
4
4 ( a 2 b2 )
внутр
M0
sin cos
ab
в
a
к1
внутр
2 в ldiag
M0

25.

Расчёт конструкций с учётом пластических деформаций
(физическая нелинейность)
Предельное равновесие пластин
Определение предельной нагрузки ( параметра Pu ) пластин
кинематическим методом ТПР
Уравнение баланса работы нагрузки
*
*
W
F D где WF P P ; D M0 M0
и энергии диссипации в пластических шарнирах:
– перемещение точки приложения сосредоточенной нагрузки P,
P P
D = D к + Dв
эпюры перемещений предельного механизма
V – объём
при равномерно распределённой нагрузке q
По кинематической теореме ТПР:
Pu P D M0 M0
P
P
контурных
внутренних
шарниров текучести
d
a
Прямоугольные пластины при равномерно распределённой нагрузке q
внутр
M0 конт
q V 1 ab
b
M 0 M0
3
конт
2
2
4
(
a
b
)
внутр
M 0 к1 b nb к2 a na
к1
M0
ab
na , nb – количества защемлённых сторон
M0
длинами a и b соответственно
qu M0
к1
q
j=1
j=2
j=3
3
1
1
12
M
2
3n a =2 2 1
2 n a = 1
0
1
1
n
=
n
=
0
к1
(
)
2
a
b
j
1
a 0 2
nb = 0
ab
nb = 0
к2 2
b
к2
к2
2
в
= a/b
j=4
4 n
a3= 1 1
2
n =1
b
j=5
5 n
a2=
2 3
n = 1 2
b
j=6
6 n a = 0 3
2
nb = 1
j=7
7n a = 0 2
n =2
b
j=8
8 n
a 3= 1 2
2
nb = 2

26.

Контрольные
ы
вопрос
( в скобках даны номера слайдов, в которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в
скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 26» )
1. Какие системы называются нелинейно деформируемыми? ( 2 )
2. Виды нелинейностей, влияющих на поведение деформируемых систем ( 2 ) .
3. Чем различаются процессы деформирования систем с мягкой и жёсткой
нелинейностями? ( 2 )
4. Чем обусловлена физическая нелинейность (ФН)? ( 3 ) Примеры расчётных моделей
нелинейного деформирования материалов ( 4 ) .
5. В чём сущность геометрической нелинейности (ГН)? ( 5 ) Примеры проявления ГН
в деформировании некоторых типов стержневых конструкций ( 6 ) .
6. Что такое конструктивная нелинейность (КН)? ( 7 ) Каков общий признак КН? ( 7 )
7. Что называется «расчётом по деформированной схеме»? ( 7 )
8. Характерные случаи проявления конструктивной нелинейности в работе
строительных конструкций ( 7, 8 ) .
9. Как классифицируются задачи расчёта нелинейно деформируемых систем по видам
нелинейностей? ( 9 ) Какие виды и сочетания нелинейностей наиболее актуальны
для строительных конструкций? ( 9 )
10. Методы расчёта нелинейно деформируемых систем ( 9 ) .
11. Понятие об упругопластическом деформировании стержневых систем в случаях
растяжения/сжатия и изгиба элементов ( 10 – 13 ) . Предельное состояние сечения
при изгибе (пластический шарнир) ( 13 ) .
12. Расчёты физически нелинейно деформируемых систем методом предельного
равновесия: основная идея определения предельной (разрушающей) нагрузки ( 14 ) .
13. Статическая, кинематическая и обобщающая (двойственная) теоремы теории
предельного равновесия ( 15 ) .
14. Применение методов теории предельного равновесия для определения предельных
нагрузок балок ( 17 – 20 ) , рам ( 21, 22 ) и пластин ( 23 – 25 ) – общие представления.
*) Только в режиме «Показ слайдов».