Похожие презентации:
Строительная механика. Расчёт трёхшарнирных систем внутренние силовые факторы. Линии влияния усилий
1. РАСЧЁТ ТРЁХШАРНИРНЫХ СИСТЕМ
СТРОИТЕЛЬНАЯ МЕХАНИКА.Часть I
РАСЧЁТ
ТРЁХШАРНИРНЫХ
СИСТЕМ
ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ.
ЛИНИИ ВЛИЯНИЯ УСИЛИЙ
2
2.
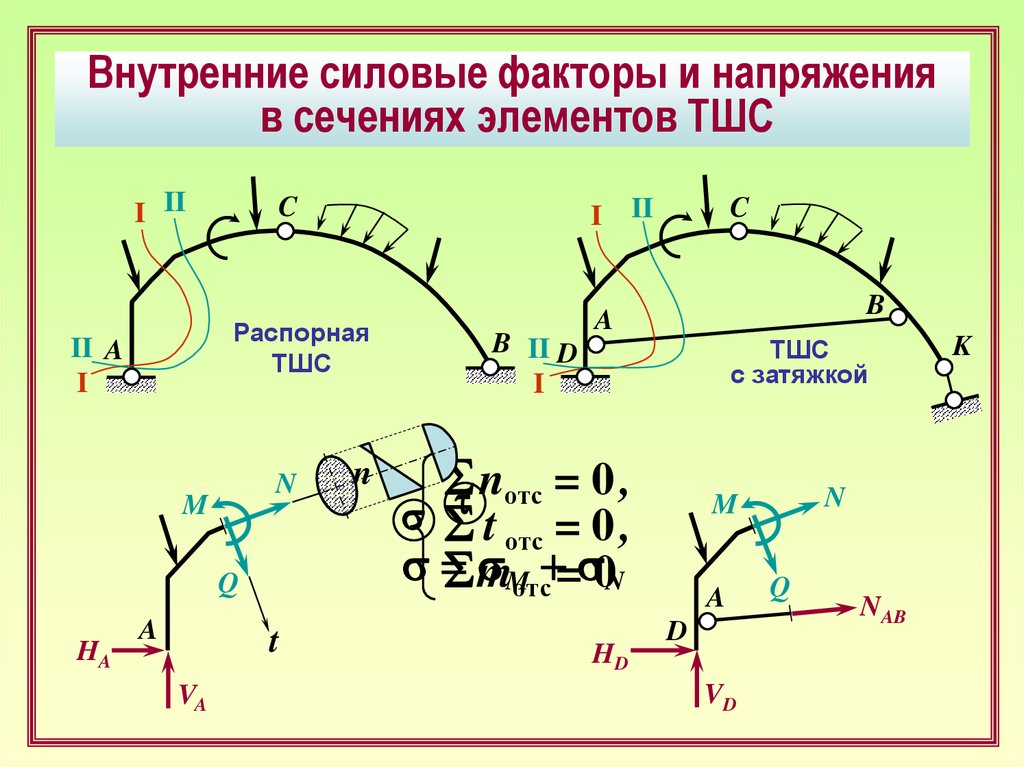
Внутренние силовые факторы и напряженияв сечениях элементов ТШС
I II
C
Распорная
ТШС
II A
I
N
M
Q
HA
I
A
t
VA
n
B II D
I
C
II
B
A
ТШС
с затяжкой
St nотс = 0 ,
s S t = 0,
отс
s=
sMотс+=s0N
Sm
HD
N
M
A
D
VD
Q
NAB
K
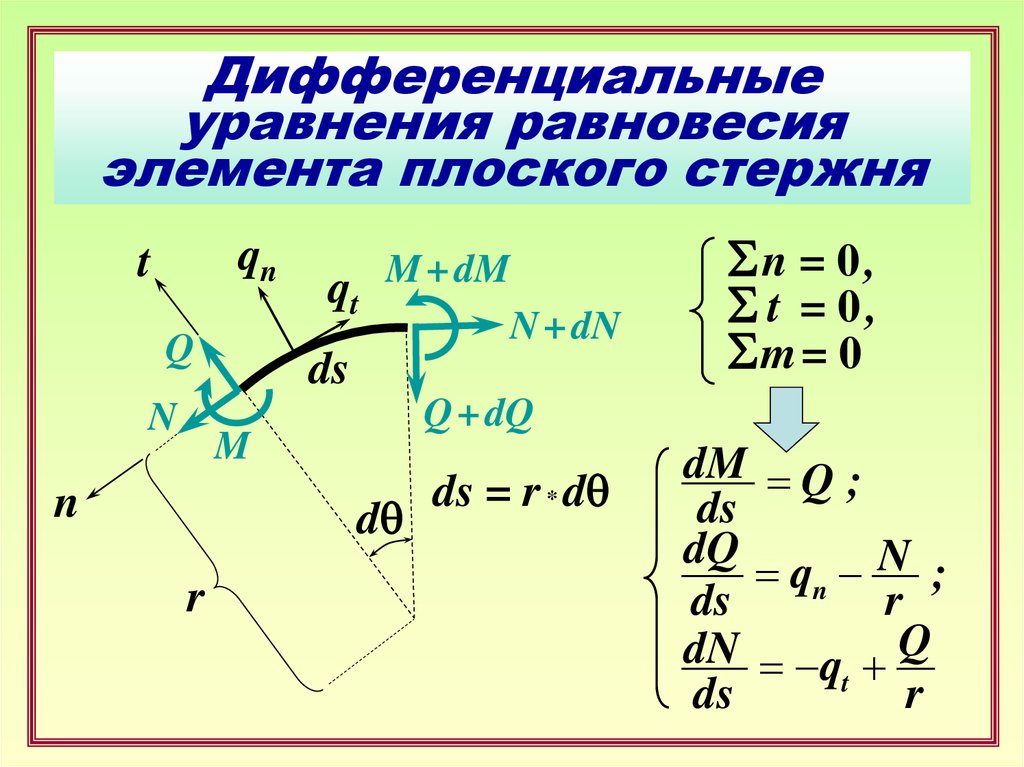
3. Дифференциальные уравнения равновесия элемента плоского стержня
qnt
Q
N
qt
M + dM
ds
Q + dQ
M
n
dq
r
N + dN
Sn = 0,
S t = 0,
Sm = 0
ds = r * dq
dM = Q ;
ds
dQ
= qn N ;
ds
r
dN = q + Q
t
ds
r
4.
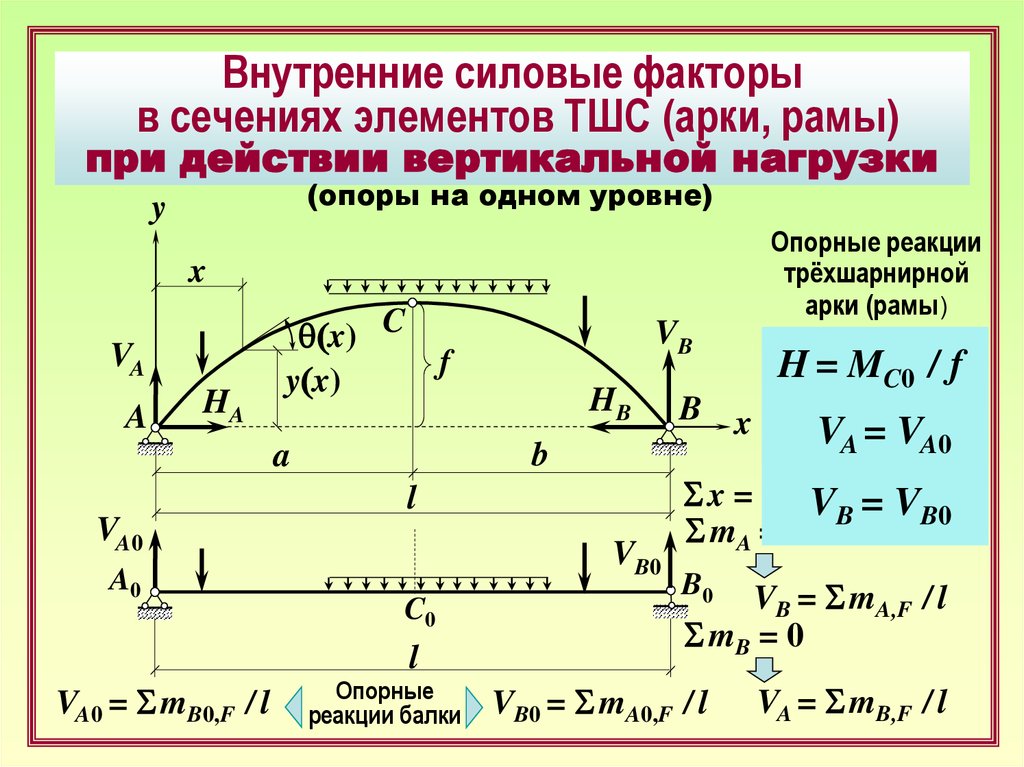
Внутренние силовые факторыв сечениях элементов ТШС (арки, рамы)
при действии вертикальной нагрузки
(опоры на одном уровне)
y
x
VA
A
HA
q(x) C
f
y(x)
VB
HB
l
VA0
A0
VB0
C0
l
VA0 = S mB0,F / l
Опорные
реакции балки
H =Опорные
MC0 / f
реакции
B x трехшарнирной
V =V
A (рамы
A0)
арки
b
a
Опорные реакции
трёхшарнирной
арки (рамы)
HA =
HVB = H
Sx = 0 V
=
B
B0
S mA = 0
B0
VB = S mA,F / l
S mB = 0
VB0 = S mA0,F / l
VA = S mB,F / l
5.
Внутренние силовые факторыв сечениях элементов ТШС (арки, рамы)
при действии вертикальной нагрузки
(опоры на одном уровне)
y
M(x) = VA* x +S mF,oтc – H* y(x)
x
M(x)
VA
A
H
VA0
N(x)
Q(x)
M0(x)
A0
M0(x)
q(x)
y(x)
M(x) = M0(x) – H* y(x)
x
Q(x) = (VA+S yF,oтc ) * cos q(x) – H* sin q(x)
Q0(x)
Примечание:
Q(x) = Q0(x) * cos q(x) – H* sin q(x)
N(x) = – (VA+S yF,oтc )* sin q(x) – H* cos q(x)
Nверш = – H; Qверш = Q0
0(x)
N(x) = – [ Q0Q(x)
* sin q(x) + H* cos q(x) ]
VA0= VA
Q0(x)
в вершине арки,
где q(x) = 0:
6.
Внутренние силовые факторы в сеченияхэлементов ТШС c опорами на разных уровнях
при действии вертикальной нагрузки
y
x
Опорные
/
V
A
реакции
VA/ = VA0 A
VB/ = VB0
H/ = MC0 / f /
H/
VB/
q(x) C
y1(x) a0
f/
H/
B
x
b
a
l
M(x) = M0(x) – H/* y1(x)
y1(x) = y(x) cos a0 – xsin a0
Q(x) = Q0(x) * cos q(x) – H/* sin [q(x) – a0]
N(x) = – { Q0(x)* sin q(x) + H/* cos [q(x) – a0]}
7.
Внутренние силовые факторы в сеченияхэлементов ТШС c опорами на разных уровнях
при действии вертикальной нагрузки
y
x
Опорные
/
V
A
реакции
Вариант:
V /= V A
A
A0
HB=/ =MVC0
V
B0
/f
H/ = MC0 / f /
H/
VB/
q(x) C f /
f
*
(x) a0
yy1(x)
H/
b
a
B
x
l
(x)
M(x) = M0(x) – H*/*yy*1(x)
y1(x) = y(x) cos a0 – xsin a0
H/
Q(x)
Q(x)= =QQ
(x)
(x)
*
cos
*
cos
q(x)
q(x)
–
–
H * sin
* sin
[q(x)
[q(x)– –aa
0 0
0]0]
cosα 0
H/
N(x)= =– –{ {QQ
(x)
*
sin
q(x)
+
H
* cos
[q(x)
–a
N(x)
(x)
*
sin
q(x)
+
* cos
[q(x)
– 0a]}
]}
0 0
0
cosα 0
8.
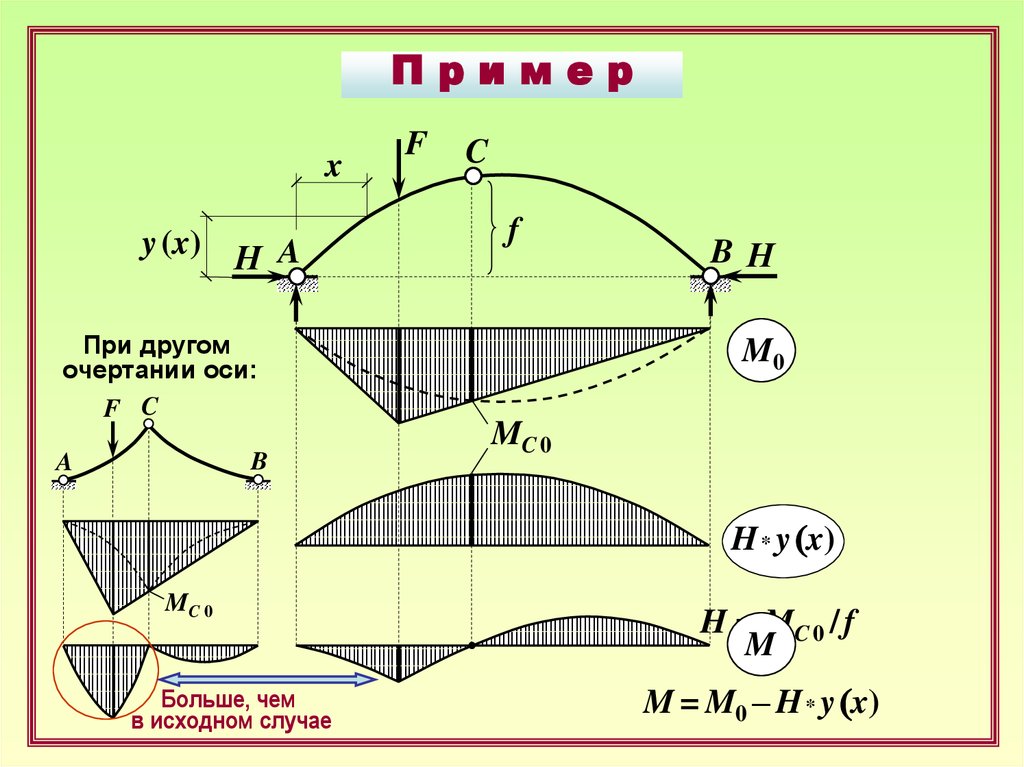
Примерx
y (x) Н A
При другом
очертании оси:
F C
B
A
F
C
f
BН
M0
MC 0
H * y (x)
MC 0
Больше, чем
в исходном случае
H = MC 0 / f
M
M = M0 – H * y (x)
9.
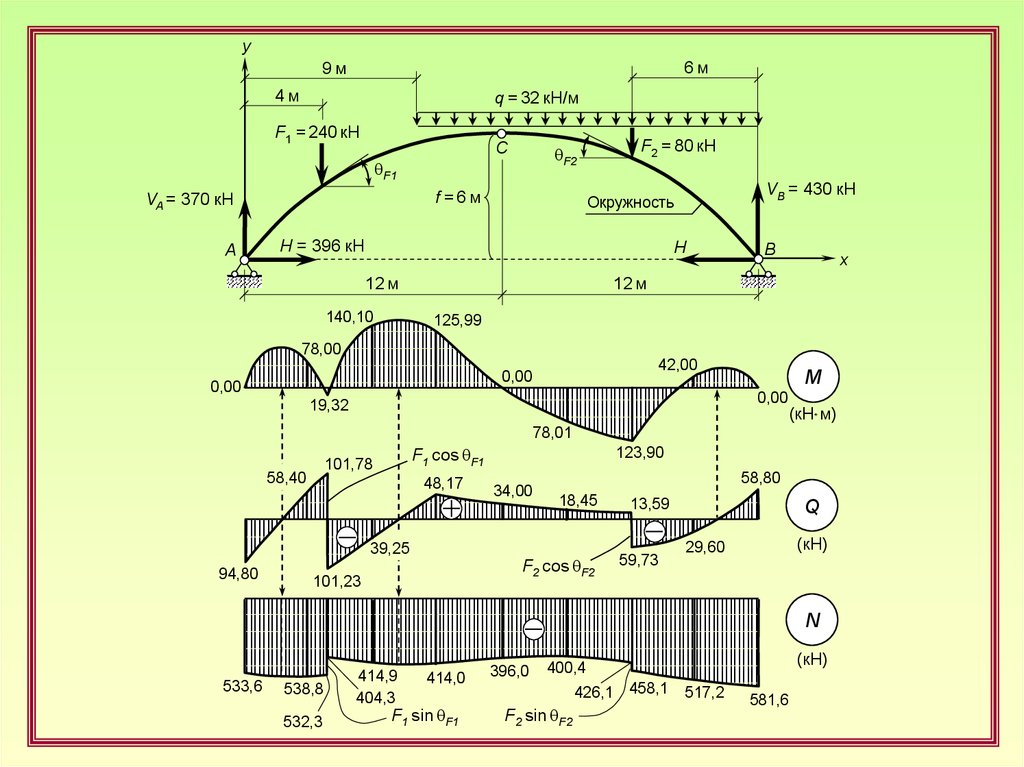
y6м
9м
4м
q = 32 кН/м
F1 = 240 кН
C
qF1
f=6м
VA = 370 кН
A
F2 = 80 кН
qF2
VB = 430 кН
Окружность
H = 396 кН
H
12 м
140,10
B
x
12 м
125,99
78,00
42,00
0,00
0,00
M
0,00
19,32
(кН* м)
78,01
F1 cos qF1
101,78
58,40
48,17
39,25
94,80
123,90
34,00
58,80
18,45
F2 cos qF2
101,23
13,59
59,73
Q
(кН)
29,60
N
533,6
538,8
532,3
414,9
404,3
414,0
F1 sin qF1
396,0
(кН)
400,4
426,1 458,1
F2 sin qF2
517,2
581,6
10.
y6м
9м
4м
q = 32 кН/м
F1 = 240 кН
F2 = 80 кН
C
Парабола
f=6м
VA = 370 кН
A
VB = 430 кН
Окружност
ь
H = 396 кН
H
12 м
B
x
12 м
140,10
78,00
0,00
0,00
123,90
42,00
M
0,00
(кН* м)
F1 cos qF1
160,00
101,78
48,17
222,00
58,80
Q
(кН)
94,80
101,23 111,49
F2 cos qF2
59,73
N
533,6
541,6
F1 sin qF1
396,0
396,0
F2 sin qF2
(кН)
581,6
584,1
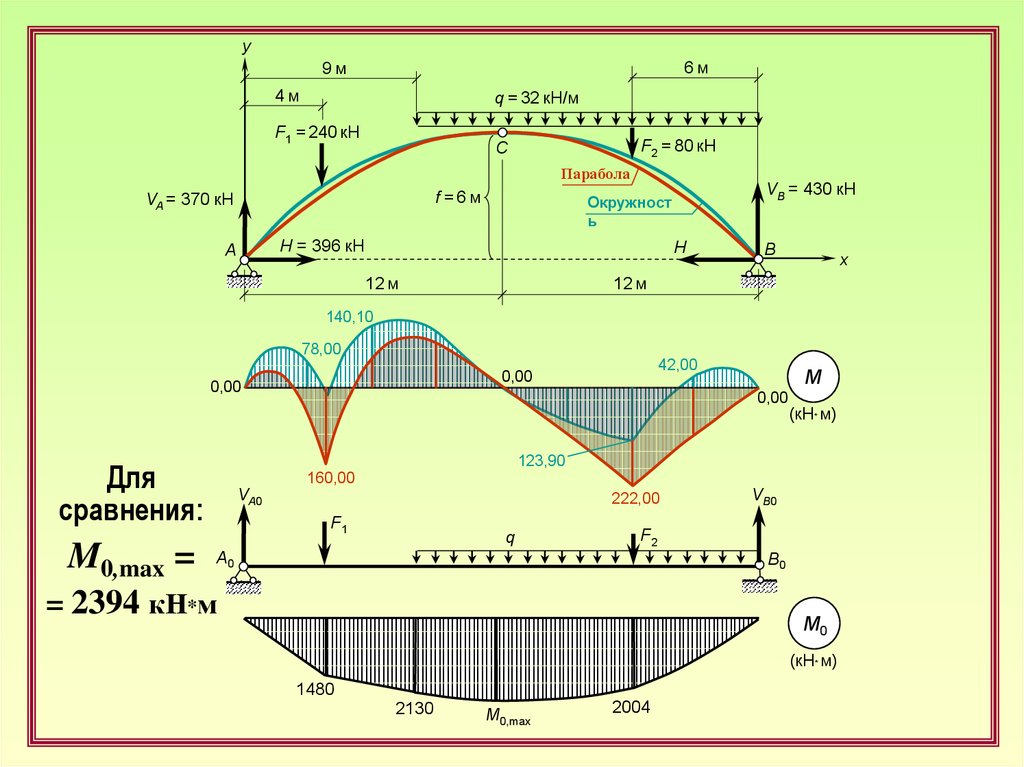
11.
y6м
9м
4м
q = 32 кН/м
F1 = 240 кН
F2 = 80 кН
C
Парабола
f=6м
VA = 370 кН
H = 396 кН
A
VB = 430 кН
Окружност
ь
H
12 м
B
x
12 м
140,10
78,00
M
0,00
(кН* м)
123,90
Для
сравнения:
M0,max =
42,00
0,00
0,00
160,00
VA0
222,00
F1
q
VB0
F2
A0
B0
= 2394 кН*м
M0
(кН* м)
1480
2130
M0,max
2004
12.
Трёхшарнирные системы (арки и рамы)с рациональным очертанием оси
Критерий рациональности – безмоментность:
М(х) = 0
Рациональное очертание оси при вертикальных нагрузках:
M(x) = M0(x) – H * y (x) = 0
y( x) = 1 M0( x)
H
Пример
A
В
M0(х)
A
С
В
13.
Трёхшарнирные системы (арки и рамы)с рациональным очертанием оси
Критерий рациональности – безмоментность:
М(х) = 0
Рациональное очертание оси при равномерной
гидростатической нагрузке ( qn = const , qt = 0 )
qn = const
Из дифференциальных уравнений равновесия:
dM = Q d (0) = 0 Q = 0
ds
ds
d (0)
dQ
N
= qn
= 0 N = qnr
ds
r
ds
dN = q + Q dN = 0 N = const = q r
t
n
ds
r
ds
r = const
– окружность
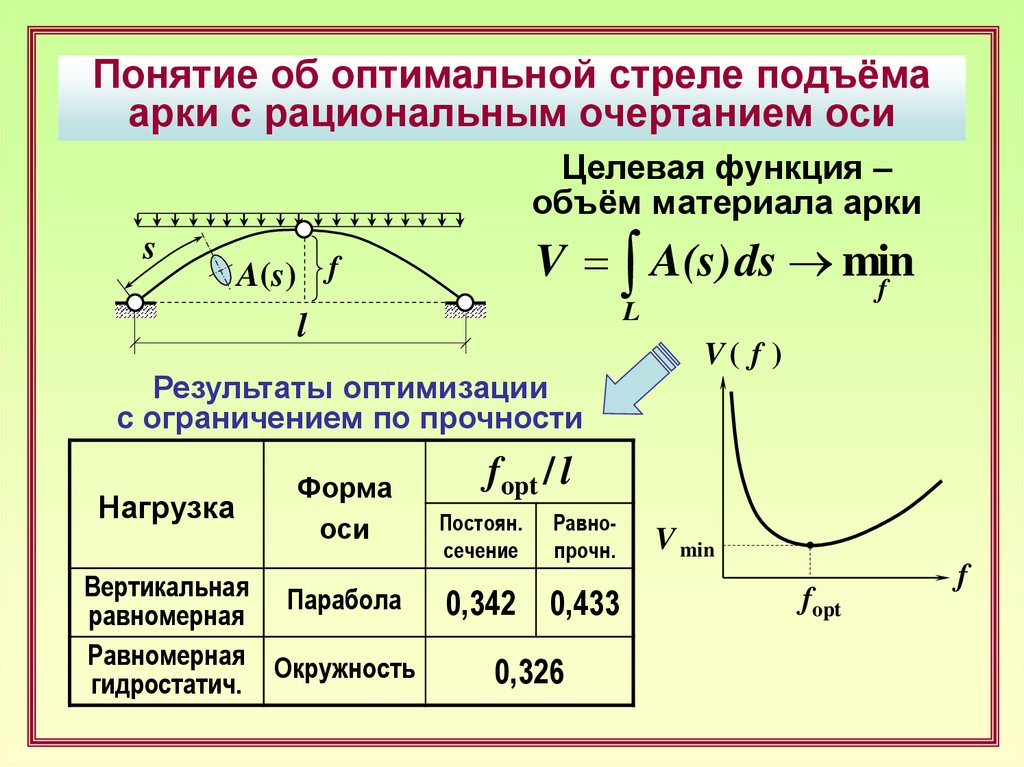
14.
Понятие об оптимальной стреле подъёмаарки с рациональным очертанием оси
Целевая функция –
объём материала арки
s
V = A(s) ds min
f
A(s) f
l
L
Результаты оптимизации
с ограничением по прочности
Нагрузка
Форма
оси
Вертикальная Парабола
равномерная
Равномерная Окружность
гидростатич.
V( f )
fopt / l
Постоян.
сечение
Равнопрочн.
0,342 0,433
0,326
V min
fopt
f
15.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
y
Линия влияния изгибающего момента
x
F=1
xK
MK(x) = M0K(x) – H(x) * yK
C
VA
K
A
H
a
yK
VB
f
H
b
l
B
x
Л.В. MK =
= Л.В. M0K –
– yK * Л.В. Н
Линии влияния опорных реакций
1
Л.В. VA = Л.В. VA0
a*b / ( f*l )
1 Л.В. V = Л.В. V
B
B0
Л.В. H
16.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
y
Линия влияния изгибающего момента
x
F=1
xK
MK(x) = M0K(x) – H(x) * yK
C
VA
K
A
H
a
yK
VB
f
H
b
l
b* xK / l
x
xK 1 K
l
yK * a * b / ( f * l )
yK * xK * b / ( f * l )
( xK / l )* (l – xK – yK * b / f )
( b / l )* ( xK – yK * a / f )
B
x
Л.В. MK =
= Л.В. M0K –
– yK * Л.В. Н
Л.В. M0K
Л.В. Н * yK
Л.В. MK
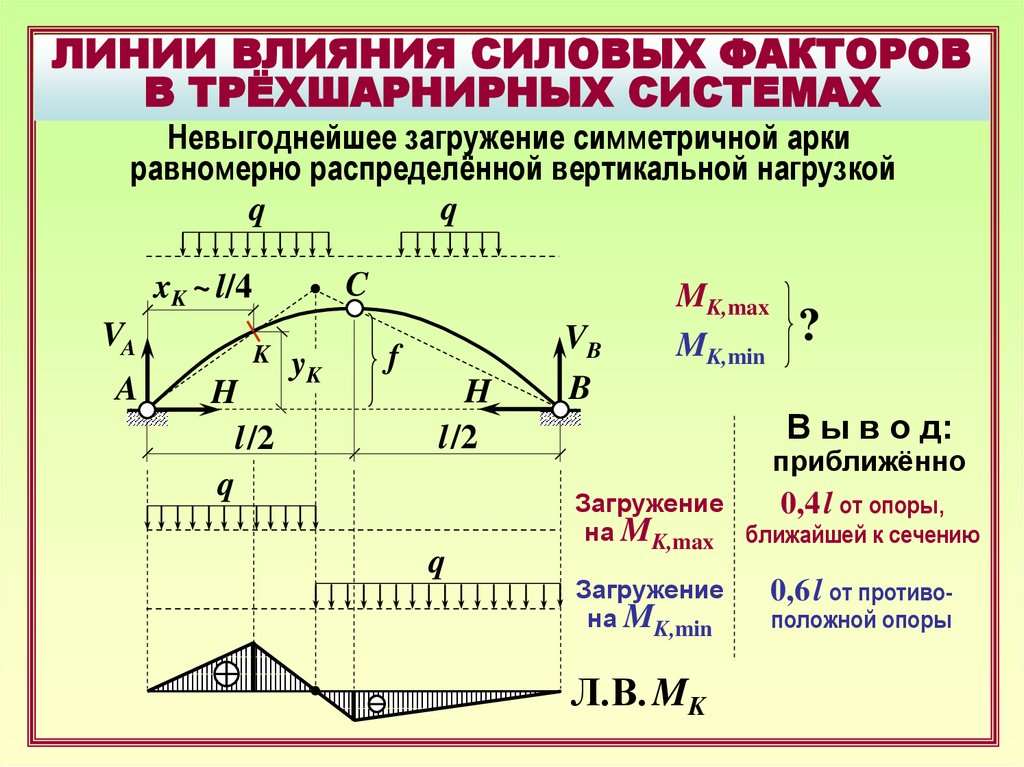
17.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
Невыгоднейшее загружение симметричной арки
равномерно распределённой вертикальной нагрузкой
q
q
C
xK ~ l/4
VA
A
K
H
l/2
q
yK
f
H
l/2
q
VB
B
MK,max
MK,min
?
В ы в о д:
приближённо
Загружение
0,4 l от опоры,
на MK,max ближайшей к сечению
Загружение
на MK,min
Л.В. MK
0,6 l от противоположной опоры
18.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
y
Линия влияния поперечной силы
x
VA
xK
F=1
qK
C
K
A
H
a
yK
QK (x) = Q0K (x) * cos qK – H(x) * sin qK
VB
f
H
B
b
l
cos qK
sin qK * xK * b / ( f * l )
cos qK
( b / l )* cos qK
sin qK * a * b / ( f * l )
Л.В. QK =
x = cos q * Л.В. Q –
K
0K
– sin qK * Л.В. Н
Л.В. Q0K * cos qK
Л.В. Н * sin qK
( b / l )*[cos qK – ( a / f ) * sin qK]
( xK / l )*[cos qK +( b / f ) * sin qK ]
Л.В. QK
19.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
y
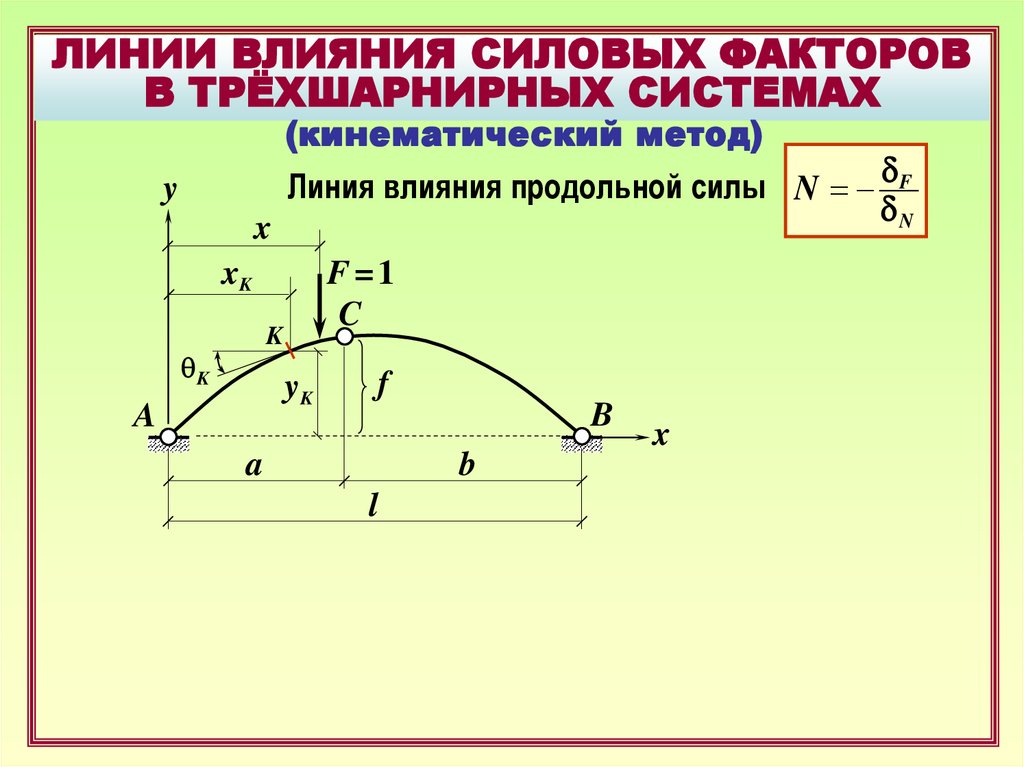
Линия влияния продольной силы
x
VA
xK
F=1
qK
C
K
A
H
a
yK
NK (x) = –[ Q0K (x) * sin qK + H(x) * cos qK]
VB
f
H
b
l
sin qK
cos qK * xK * b / ( f * l )
( b / l )* sin qK
cos qK * a * b / ( f * l )
sin qK
( xK / l )*[sin qK – ( b / f ) * cos qK]
B
Л.В. NK =
x
= – sin qK * Л.В. Q0K –
– cos qK * Л.В. Н
Л.В. Q0K * sin qK
Л.В. Н * cos qK
Л.В. NK
– ( b / l )*[sin qK + ( a / f ) * cos qK]
20.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
(кинематический метод)
F
S=
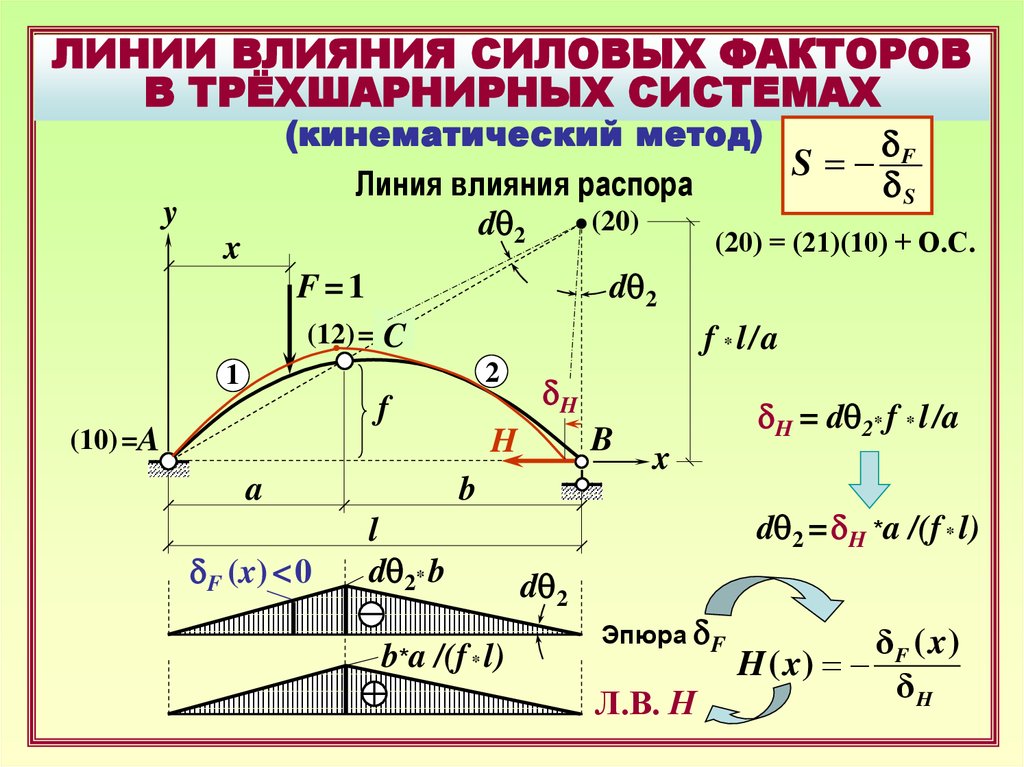
Линия влияния распора
S
y
(20)
x
(20) = (21)(10) + О.С.
F=1
(12)
C= C
f * l/a
2
1
f
(10) =A
H
a
b
l
B
x
21.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
(кинематический метод)
S= F
Линия влияния распора
S
(20)
dq2
(20) = (21)(10) + О.С.
y
x
F=1
dq2
(12) = C
f * l/a
2
1
f
(10) =A
H
B
H
a
F (x) <0
b
l
dq2* b
b*a /(f * l)
H = dq2* f * l /a
x
dq2 = H *a /(f * l)
dq2
Эпюра F
Л.В. Н
δ F ( x)
H ( x) =
δH
22.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
y
x
(кинематический метод)
Линия влияния изгибающего момента M = F
M
F=1
xK
C = (23)
(12) = K
(10) = A
1
2
MK yK
3
f
a
b
l
B = (30)
x
23.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
(кинематический метод)
Линия влияния изгибающего момента M = F
M
uM
y
(20) = (21)(10) + (23)(30)
xK
(20)C = (23)
(12) = K
(10) = A
1
x
2
MK yK
3
f
a
M
xK
1
y
b
tgψ
uM = l
tgξ + tgψ
B = (30)
x
tgy = f / b
tgx = yK / xK
l
Эпюра F
Л.В. MK
MK (x) =
δF ( x )
δM
24.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
(кинематический метод)
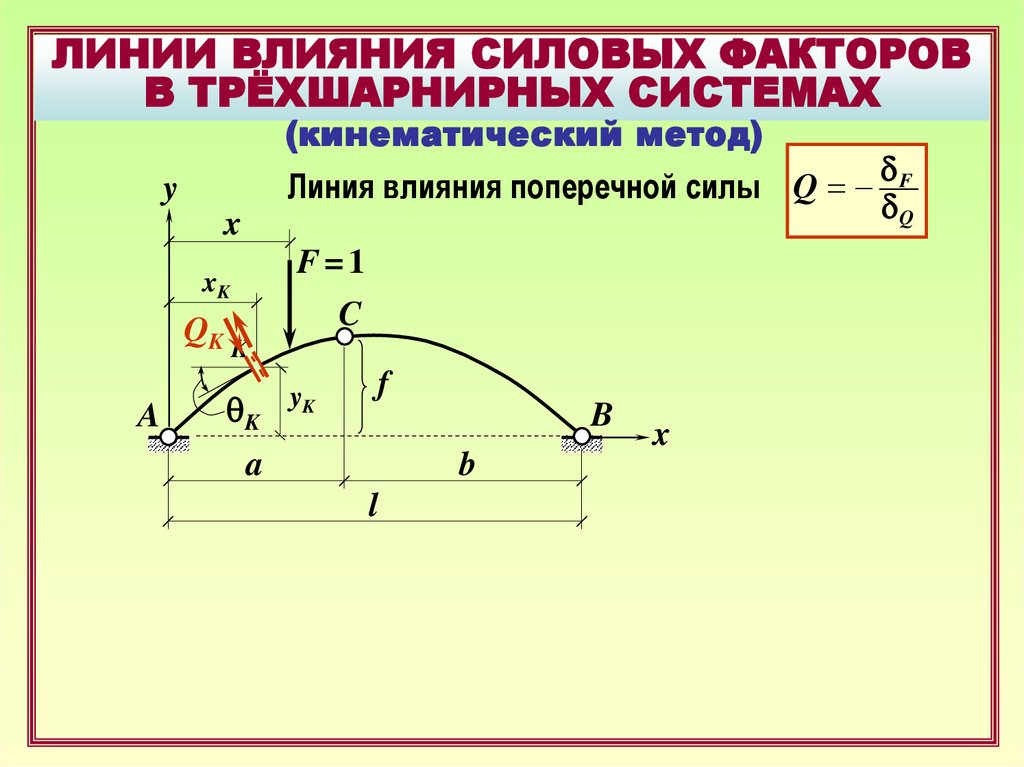
Линия влияния поперечной силы Q =
y
x
F=1
xK
C
QK K
A
qK
yK
f
B
a
b
l
x
F
Q
25.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
(кинематический метод)
y
uQ
(12)
xK
C
QK
(10) = A
1
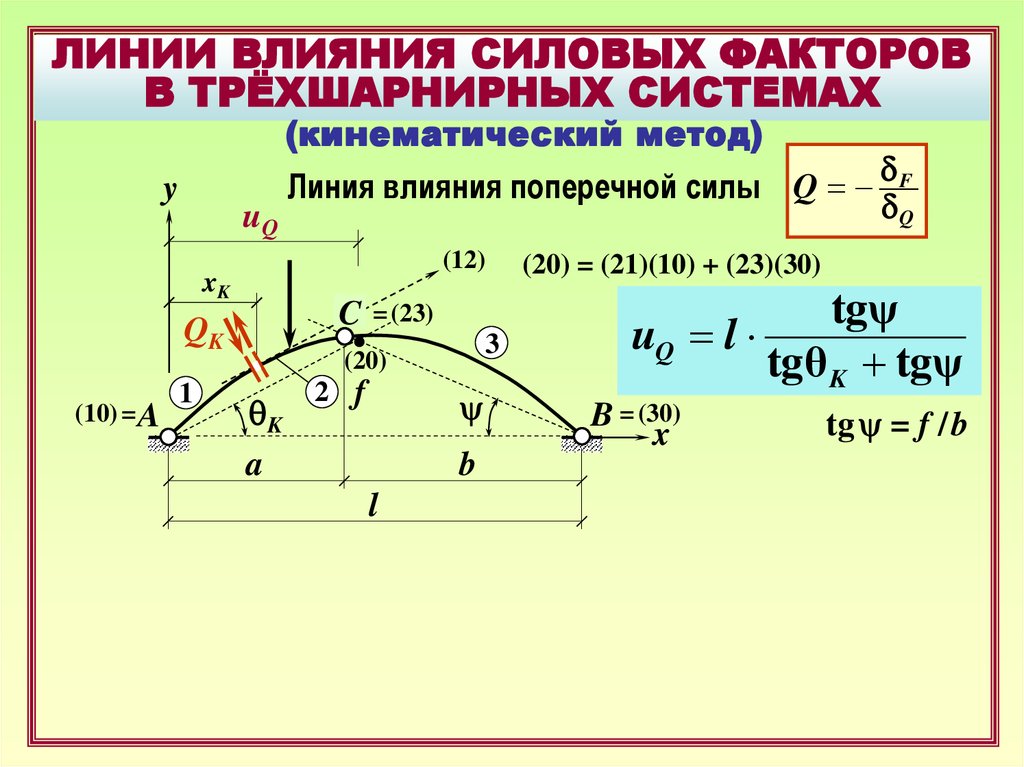
Линия влияния поперечной силы Q =
= (23)
3
(20)
qK
a
2 f
y
b
l
F
Q
(20) = (21)(10) + (23)(30)
tgψ
uQ = l
tgθ K + tgψ
B = (30)
x
tg y = f / b
26.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
(кинематический метод)
y
uQ
(12)
xK
C
QK
(10) = A
1
Линия влияния поперечной силы Q =
= (23)
3
(20)
qK
a
2 f
y
b
(20) = (21)(10) + (23)(30)
tgψ
uQ = l
tgθ K + tgψ
B = (30)
x
l
cos qK
F
Q
Л.В. QK
tg y = f / b
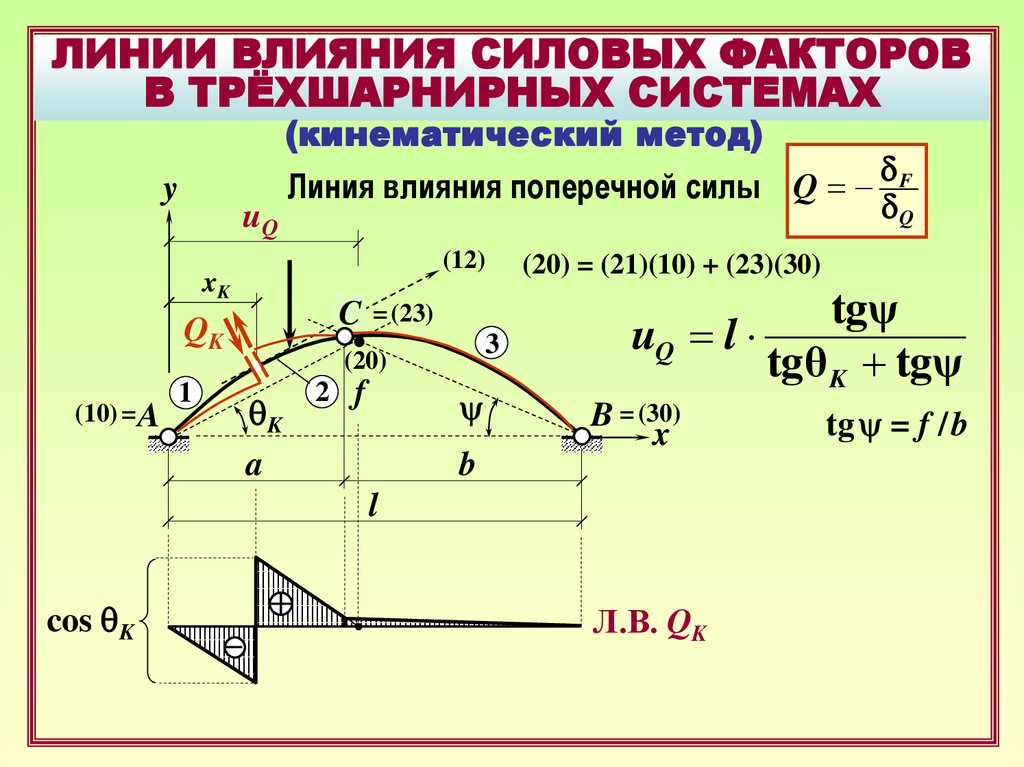
27.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
(кинематический метод)
y
uQ
xK
Линия влияния поперечной силы Q =
(12)
(20) = (21)(10) + (23)(30)
(20) C = (23)
3
QK
(10) = A
1
qK
a
2 f
y
b
tgψ
uQ = l
tgθ K + tgψ
B = (30)
x
l
cos qK
F
Q
Л.В. QK
tg y = f / b
28.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
(кинематический метод)
y
x
Линия влияния продольной силы N = F
N
xK
F=1
C
K
qK
yK
A
f
B
a
b
l
x
29.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
(кинематический метод)
(12)
y
(20)
x
uN
qK
Линия влияния продольной силы N = F
N
(20) = (21)(10) + (23)(30)
2
3
qK
(10) = A
F=1
C = (23)
NK
1
f
a
y
b
tgψ
uN = l
ctgθ K tgψ
B = (30)
x
l
sin qK
Л.В. NK
tgy = f / b
30.
ЛИНИИ ВЛИЯНИЯ СИЛОВЫХ ФАКТОРОВВ ТРЁХШАРНИРНЫХ СИСТЕМАХ
(кинематический метод)
y
Линия влияния продольной силы N = F
N
F=1
(20) = (21)(10) + (23)(30)
x
C
= (23)
xK
2
(12)
K
qK
(10) = A
f
NK
1
qK
y
yK
a
tgy = f / b
B = (30)
x
b
l
sin qK
3
tgψ
uN = l
tgψ ctgθK
uN
(20)
Л.В. NK
31.
Контрольные вопросысамостоятельно
( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 30» )
1. Какие усилия возникают в произвольном сечении арки? ( 2 )
2. Дифференциальные уравнения равновесия элемента криволинейного стержня. ( 3 )
3. Как определяются вертикальные составляющие опорных реакций
трёхшарнирной арки с опорами на одном уровне в случае вертикальной нагрузки? ( 4 )
4. Как зависит распор трёхшарнирной арки от стрелы подъёма? ( 4 )
5. Почему ключевой шарнир трёхшарнирной арки располагают обычно в её вершине? ( 4 )
6. Формула для изгибающих моментов в трёхшарнирной арке при вертикальной
нагрузке. ( 5 )
7. Изгибающие моменты в арке больше или меньше моментов в балке того же пролёта
при той же вертикальной нагрузке? Почему? ( 5 )
8. Формула для поперечных сил в трёхшарнирной арке при вертикальной нагрузке. ( 5 )
9. Формула для продольных сил в трёхшарнирной арке при вертикальной нагрузке. ( 5 )
10. Особенности очертания эпюр ВСФ в трёхшарнирных арках.
11. Как используются дифференциальные зависимости между усилиями
в криволинейном стержне для построения и проверки эпюр ВСФ в арке?
12. Какую особенность имеет эпюра Q в арке в месте приложения сосредоточенной
силы F ?
13. Какую особенность имеет эпюра N в арке в месте приложения сосредоточенной
нагрузки F ?
14. Чему равна поперечная сила в сечении в вершине арки? ( 5 )
15. Чему равна продольная сила в сечении в вершине арки? ( 5 )
16. Почему трёхшарнирная арка экономичнее по расходу материала,
чем балка того же пролёта? ( самостоятельно )
17. Что такое арка рационального очертания? ( 11 )
____________________________________________________________
*)
Только в режиме «Показ слайдов»
32.
Контрольные вопросы( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 31» )
18. Главное свойство арки рационального очертания. ( 11 )
19. Какие усилия возникают в арке рационального очертания? ( 11 )
20. Каково рациональное очертание оси арки при равномерно распределённой
по всей её длине гидростатической нагрузке? ( 12 )
21. Уравнение оси арки рационального очертания при вертикальной нагрузке. ( 11 )
22. Каково рациональное очертание оси арки при равномерно распределённой
по всему пролёту вертикальной нагрузке? ( самостоятельно, по аналогии с ( 11 ) )
23. Какое очертание оси арки – параболическое или эллиптическое – выгоднее
при вертикальных нагрузках, приложенных вблизи от опор? ( самостоятельно )
24. Какой вид имеет линия влияния распора трёхшарнирной арки с опорами
на одном уровне? ( 14 )
25. Какой вид имеет линия влияния изгибающего момента в произвольном сечении
трёхшарнирной арки? ( 22 )
26. Какой вид имеет линия влияния поперечной силы в сечении арки, расположенном
слева (справа) от ключевого шарнира? ( 25 ) ( 26 )
27. Чему равен скачок на Л.В. Q в сечении трёхшарнирной арки? ( 25 ) ( 26 )
28. Какой вид имеет линия влияния продольной силы в сечении арки левее ( правее )
ключевого шарнира? ( 28 ) ( 29 )
29. Чему равен скачок на Л.В. N в сечении трёхшарнирной арки? ( 28 ) ( 29 )
30. Какое загружение равномерно распределённой нагрузкой для симметричной арки
более опасное – по всему пролёту или по его половине? ( 16 )
31. При каком загружении трёхшарнирной арки равномерной временной нагрузкой
в её сечениях возникают наибольшие по абсолютной величине продольные силы?
( самостоятельно )
_____________________________________________________
*) Только в режиме «Показ слайдов»



















 Механика
Механика Строительство
Строительство








