Похожие презентации:
Работа электростатического поля
1. Тема урока
Работаэлектростатического
поля
2. Работа электростатического поля
A1 2 E q dÀ2 3 0,
ò.ê. cos 90 0 0
À1 3 E q l cos
E q d
3. Вывод 1
Работа не зависит от пути иформы
траектории
4. Работа электростатического поля
A1 2 E q dÀ2 1 E q d
À1 2 1 0
5. Вывод 2
Работа по замкнутому контуруравна нулю
6.
• Работа электростатическихсил не зависит от формы
пути, а только лишь от
координат начальной и
конечной точек
перемещения. Следовательно,
силы поля консервативны, а
само поле – потенциально.
7.
• электростатическое полепотенциально.
Следовательно, можно
ввести функцию состояния,
зависящую от координат –
потенциальную энергию.
8.
• Исходя из принципа суперпозиции сил ,F Fk
k
• можно показать, что общая работа А
будет равна сумме работ каждой силы:
A Ak .
k
• Здесь каждое слагаемое не зависит от
формы пути, следовательно, не зависит
от формы пути и сумма.
9. Работу сил электростатического поля можно выразить через убыль потенциальной энергии – разность двух функций состояний:
A12 W1 W2 .Работу сил
электростатического поля
можно выразить через
убыль потенциальной
энергии – разность двух
функций состояний:
10. Потенциал. Разность потенциалов
• скалярную величину,являющуюся
энергетической
характеристикой
собственно поля –
потенциал:
W
φ .
q'
11.
• Из этого выражения следует,что потенциал численно равен
потенциальной энергии,
которой обладает в данной
точке поля единичный
положительный заряд.
12.
• для потенциала точечногозаряда следующее
выражение:
1 q
φ
.
4 πε 0 r
13.
• физический смысл имеет непотенциал, а разность потенциалов,
поэтому договорились считать, что
потенциал точки, удаленной в
бесконечность, равен нулю.
• Когда говорят «потенциал такой-то
точки» – имеют в виду разность
потенциалов между этой точкой и
точкой, удаленной в бесконечность.
14.
• Другое определение потенциала:A
φ
q
или
A qφ
• т.е. потенциал численно равен работе,
которую совершают силы поля над
единичным положительным зарядом при
удалении его из данной точки в
бесконечность
• (или наоборот – такую же работу нужно
совершить, чтобы переместить единичный
положительный заряд из бесконечности в
данную точку поля). При этом
, если
q > 0. φ 0
15.
• Выразим работу сил электростатическогополя через разность потенциалов между
начальной и конечной точками:
•A
12 W1 W2 φ1q φ 2 q q φ1 φ 2 .
• Таким образом, работа над зарядом q равна
произведению заряда на убыль потенциала:
A q φ1 φ 2 qU ,
• где U – напряжение.
A qU
16.
• Формулу A qφможно использовать
для установления единиц потенциала:
• за единицу φ принимают потенциал в такой
точке поля, для перемещения в которую из
бесконечности единичного положительного
заряда необходимо совершить работу
равную единице.
• В СИ единица потенциала 1 В 1 Дж/1 Кл
• Электрон - вольт (эВ) – это работа,
совершенная силами поля над зарядом,
равным заряду электрона при прохождении
им разности потенциалов 1 В, то есть:
1 эВ 1,6 10
19
Кл В 1,6 10
19
Дж.
17. Связь между напряженностью и потенциалом
• эта работа, если она совершенаэлектростатическим полем, равна
убыли потенциальной энергии заряда,
перемещенного на расстоянии dl:
dφ
El .
dl
18.
• эта работа, если она совершенаэлектростатическим полем, равна убыли
потенциальной энергии заряда,
перемещенного на расстоянии dl:
d
A
q
d
φ
;
E
q
d
l
q
d
φ
l
• отсюда
dφ
(3.4.2 ) El
dl
.
19. Силовые линии и эквипотенциальные поверхности
• Направление силовой линии (линии напряженности)в
каждой точке совпадает с направлением E .
• Отсюда следует, что напряженность равна разности
потенциалов U на единицу длины силовой линии.
• Именно вдоль силовой линии происходит максимальное
изменение потенциала. Поэтому всегда можно определить
между двумя точками, измеряя U между ними,
причем тем точнее, чем ближе точки.
• В однородном электрическом поле силовые линии –
прямые. Поэтому здесь определить наиболее просто:
φ
U
E
l
E
20.
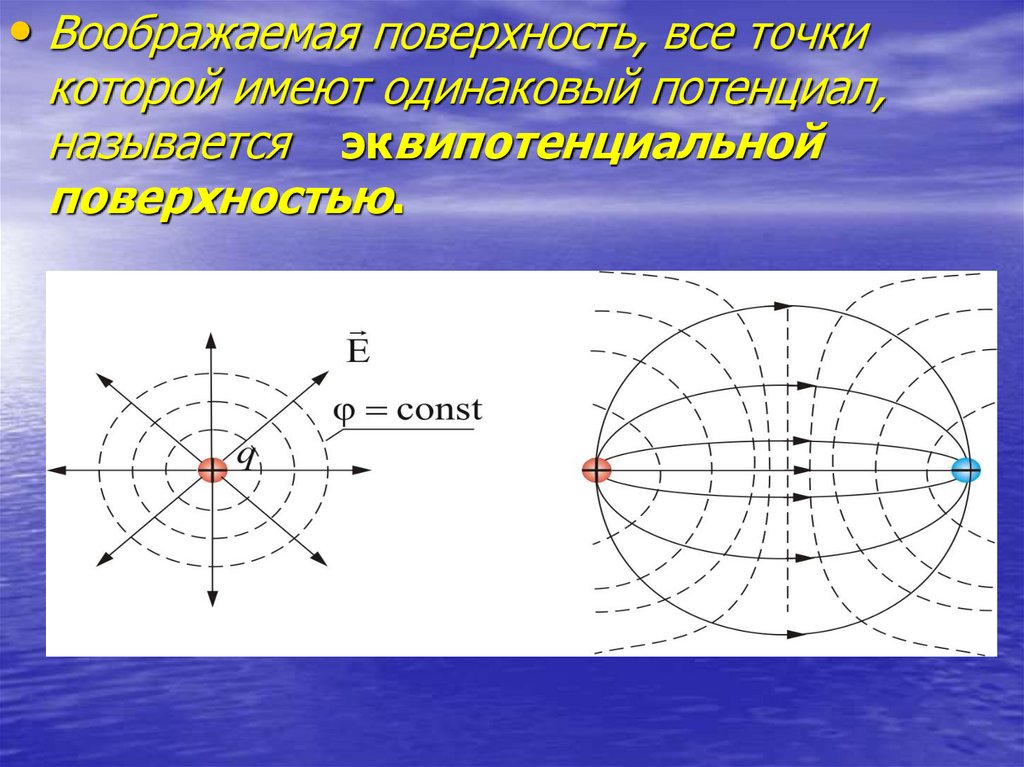
• Воображаемая поверхность, все точкикоторой имеют одинаковый потенциал,
называется эквипотенциальной
поверхностью.
21.
Линии напряженности и эквипотенциальныеповерхности взаимно перпендикулярны
22.
• Из обращения в нуль циркуляции вектораследует, что линии электростатического
поля не могут быть замкнутыми: они
начинаются на положительных зарядах
(истоки) и на отрицательных зарядах
заканчиваются (стоки) или уходят в
бесконечность





















 Физика
Физика








