Работа в электростатическом поле

1. Работа в электростатическом поле Потенциал Связь между напряженностью и потенциалом Диполь

ВоГУ
Лекция 21 (3)
Работа в электростатическом поле
Потенциал
Связь между напряженностью и
потенциалом
Диполь
Кузина Л.А.,
к.ф.-м.н., доцент
2017 г.
1

2. План

2

3.

Работа по перемещению заряда в электростатическом поле
Работа электростатических сил по перемещению
точечного заряда q в поле заряда Q:
dA F dl F cos dl F dr
F qE
dA qE dr
E
Q
4 0 r 2
2
A12 dA
1
3

4.

dA qE dr
E
Q
4 0 r 2
2
r2
r2
A12 dA qE dr q
1
r1
r1
Q
4 0 r
2
A12 dA
1
2
r2
r2
1
1
dr
qQ 1
qQ 1
A12
2 dr
4 0 r r
4 0 r r
r2
qQ 1
A12
4 0 r r
1
qQ 1 1
A12
4 0 r2 r1
4

5.

По закону сохранения энергии работа совершается
за счёт уменьшения потенциальной энергии
взаимодействия зарядов:
A12 W W2 W1
qQ 1 1
A12
4 0 r2 r1
qQ 1
W
const
4 0 r
qQ
W
4 0 r
W 0 при
r

6.

Потенциальный характер электростатического поля.
Теорема о циркуляции
qQ 1 1
A12
4 0 r2 r1
Работа не зависит от траектории, а только от начального и
конечного положения заряда q.
Электростатическое поле потенциально
Потенциальны поля только неподвижных зарядов
Для замкнутой траектории: r1 r2
qQ 1 1
0
A
4 0 r2 r1
A dA 0
L
6

7.

A dA 0
L
dA F dl
F qE
A dA qEdl q Edl 0
L
Циркуляция вектора напряжённости:
L
L
Edl 0
L
Теорема о циркуляции:
циркуляция вектора напряжённости электростатического
поля по произвольному замкнутому контуру равна нулю
7

8.

Для того, чтобы векторное поле было потенциально,
необходимо и достаточно, чтобы циркуляция вектора
напряжённости поля по произвольному замкнутому контуру
была равна нулю, то есть:
Edl 0
Поле потенциально
L
Потенциальны только поля НЕПОДВИЖНЫХ зарядов
8

9.

Потенциал
Определение:
Потенциал данной точки поля – это энергия единичного
положительного точечного пробного заряда, помещённого
в данную точку:
W
q
Дж
В
Кл
Потенциал –
скалярная энергетическая
характеристика поля
Энергия заряда q в точке поля с потенциалом φ:
W q
9

10.

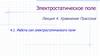
Потенциал
Ещё определение:
Потенциал данной точки поля численно равен работе по
перемещению единичного точечного пробного
положительного заряда из данной точки поля на
бесконечность
A
q
Определения эквивалентны:
W
q
A W W W W
10

11.

Потенциал поля, созданного точечным
зарядом Q на расстоянии r:
qQ
W
4 0 r
W
q
точечн.зар.
Q
4 0 r

12.

Принцип суперпозиции
Потенциал, созданный в данной точке системой зарядов qi,
равен алгебраической сумме потенциалов, созданных в
данной точке каждым зарядом системы в отдельности
i
i
В случае непрерывно распределённых зарядов:
d
V
d
dq
4 0 r
12

13.

Энергия системы точечных зарядов
1
W qi i
2 i
Потенциал, созданный всеми
зарядами системы, кроме заряда qi ,
в точке, где находится i-тый заряд
13

14.

Связь между напряженностью и потенциалом
dA F dl F dr
F qE
dA dW
W q
dA qE dr
dA qd
qE dr qd
E dr d
14

15.

E dr d
E grad
Ex
x
Градиент (grad) скалярной величины –
вектор, направленный в сторону
наибольшего возрастания этой
величины, показывает быстроту
изменения этой величины в
пространстве
grad
i
j
k
x
y
z
grad
Вектор напряжённости направлен в сторону
наибольшего УБЫВАНИЯ потенциала
Для однородного поля:
E
x
15

16.

Связь между напряженностью и потенциалом
A12 W W2 W1 q 2 q 1 q
F qE
A12 q
2
A12 dA F dl q E dl
2
2
1
1
1
2 1 E dl
2
1
16

17.

Связь между напряженностью и потенциалом
Можно иначе:
E dr d d E dl
2
d
1
E dl
2
1
Для однородного поля:
E
x
17

18.

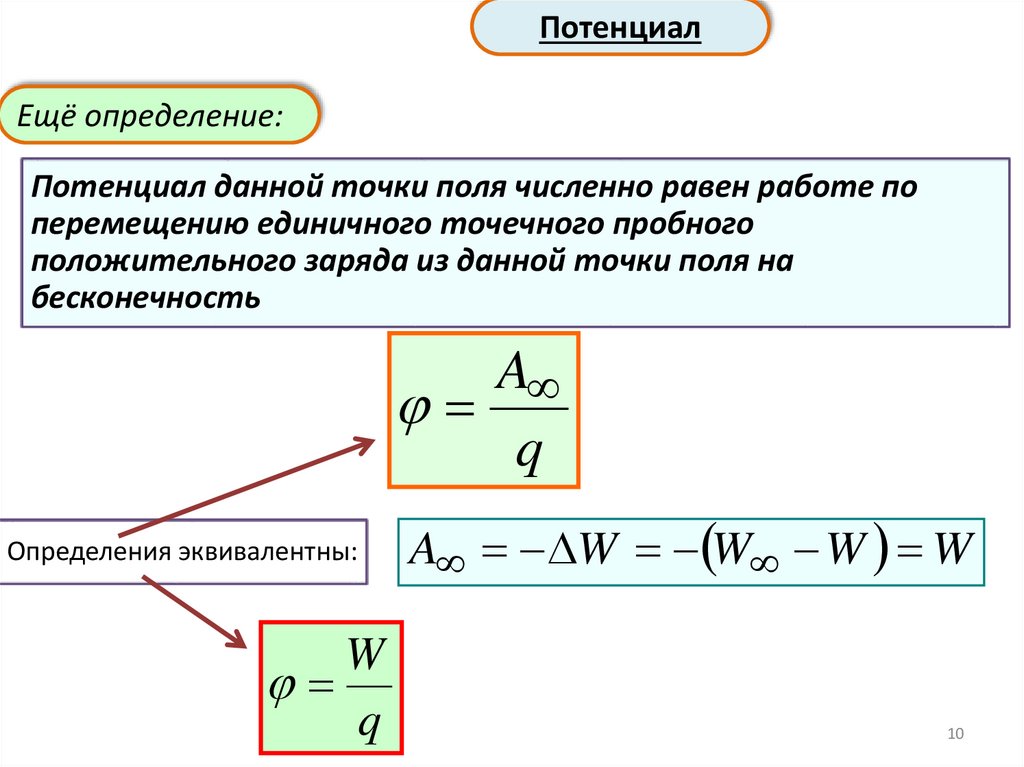
Потенциал. Эквипотенциальные поверхности
Эквипотенциальная поверхность – совокупность
точек пространства, где φ=const
Линии напряжённости всегда перпендикулярны
эквипотенциальным поверхностям
18

19.

20.

Эквипотенциальные поверхности
20

21.

Эквипотенциальные поверхности
21

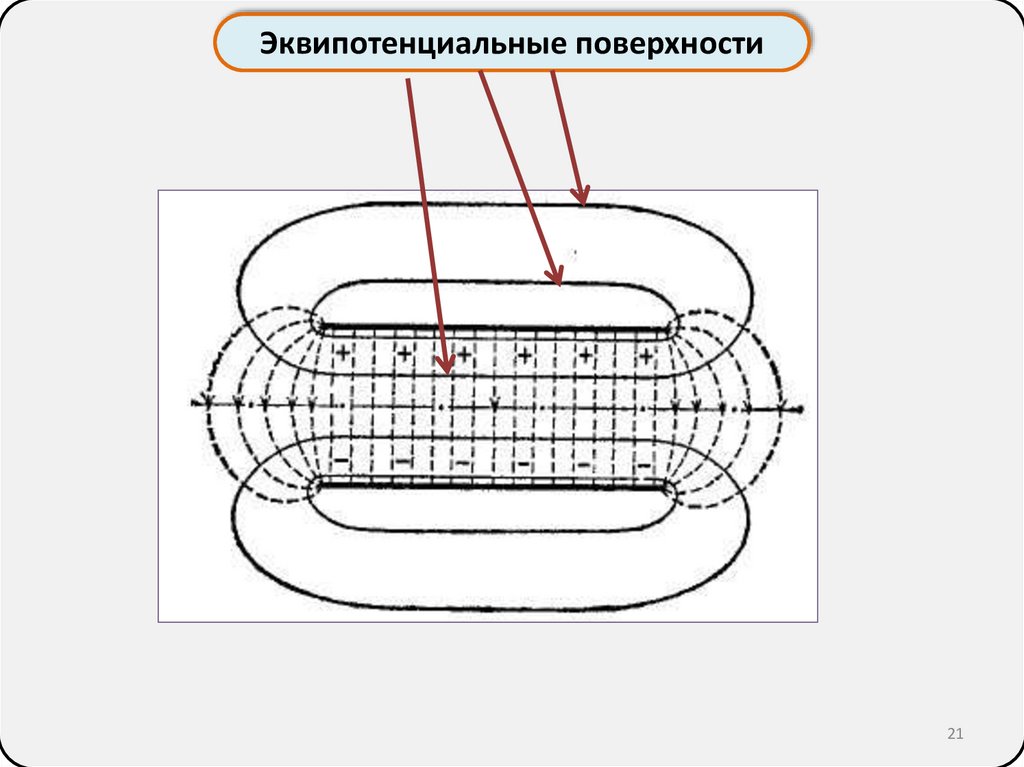
22.

Электрический диполь
Определение:
Электрический диполь - система двух одинаковых по
величине противоположных по знаку точечных
зарядов
pe q l
l
- электрический дипольный момент
– плечо диполя
22

23.

Электрический диполь в однородном поле
F1 F2 F qE
Диполь в электрическом поле ориентируется по полю
23

24.

Электрический диполь в однородном поле
F1 F2 F qE
Силы равны и противоположны
Это пара сил
Момент пары:
M F d F l sin
M qE l sin ql E sin pe E sin
M pe E
24

25.

Энергия диполя в электростатическом поле
Работа dA внешних сил по повороту диполя на угол dα>0 идёт на
увеличение энергии диполя в электрическом поле: dA dW
dA M d
dW M d
M pe E sin
dW
M pe E sin
d
W pe E cos
W pe E
25

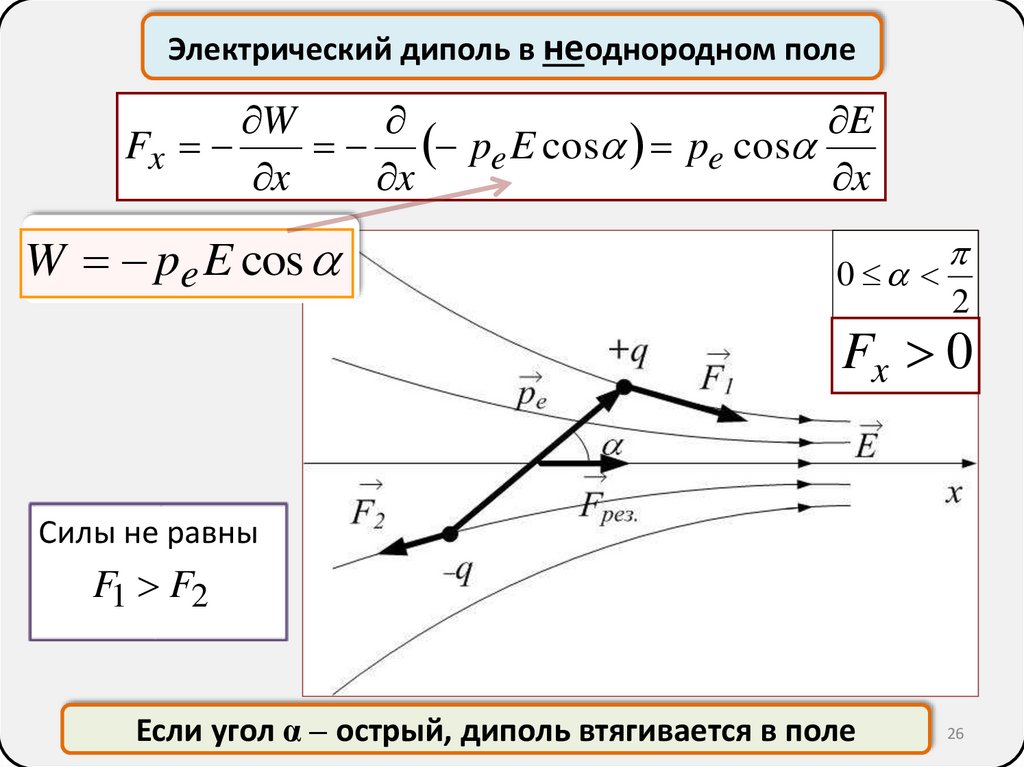
26.

Электрический диполь в неоднородном поле
W
E
Fx
pe E cos pe cos
x
x
x
W pe E cos
0
2
Fx 0
Силы не равны
F1 F2
Если угол α – острый, диполь втягивается в поле
26

27.

Электрический диполь в неоднородном поле
Если угол α – тупой, диполь выталкивается из поля
F1 F2
2
E
Fx pe cos
x
Fx 0
Свободный диполь сначала ориентируется по полю,
а затем втягивается в область сильного поля
27

28.

Электрическое поле, созданное точечным диполем
28

29.

Потенциал поля, созданного точечным диполем
q
4 0 r
q
4 0 r
l
r r cos
2
l
r r cos
2
29

30.

Потенциал поля, созданного точечным диполем
q
4 0 r
q
4 0 r
l
r r cos
2
l
r r cos
2
q
1
1
4 0 r l cos r l cos
2
2
l
l
r
cos
r
cos
q
l cos
q l cos
2
2
q
2
2
l
l
4 0
4 0 2 l
4
r
0
r cos r cos
r cos
2
2
2
30

31.

Потенциал поля, созданного точечным диполем
q l cos
4 0 r 2
31

32.

Напряжённость поля, созданного точечным диполем
E grad
E
E
x
r
x
r
E E y
y r
y r
32

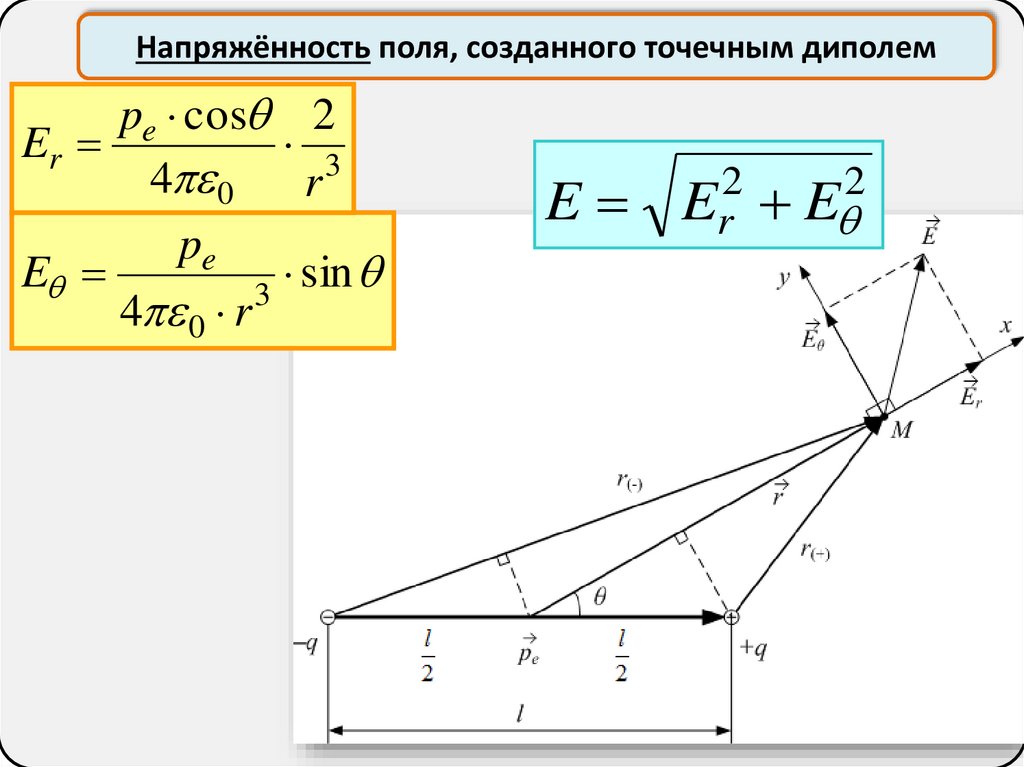
33.

Напряжённость поля, созданного точечным диполем
q l cos
4 0 r 2
pe cos pe cos 2
Er
3
r
r 4 0 r 2
4 0
r
33

34.

Напряжённость поля, созданного точечным диполем
q l cos
4 0 r 2
1 pe cos
E
r
r 4 0 r 2
pe
cos
E
3
4 0 r
pe
E
sin
3
4 0 r
34

35.

Напряжённость поля, созданного точечным диполем
pe cos 2
Er
3
4 0
r
pe
E
sin
3
4 0 r
E
2
Er
E
2
35

36.

Напряжённость поля, созданного точечным диполем
Er
pe cos 2
pe
3 E
sin
3
4 0
r
4 0 r
E Er2 E 2
2
pe cos 2
p
e
E
3
sin
3
4
r
4
r
0
0
E
E
E
pe
4 0 r
3
pe
4 0 r
pe
4 0 r
3
2 cos
2
2
sin
2
4 cos2 1 cos2
2
1
3
cos
3
36

37.

Напряжённость поля, созданного точечным диполем
E
pe
4 0 r
1
3
cos
3
2
37

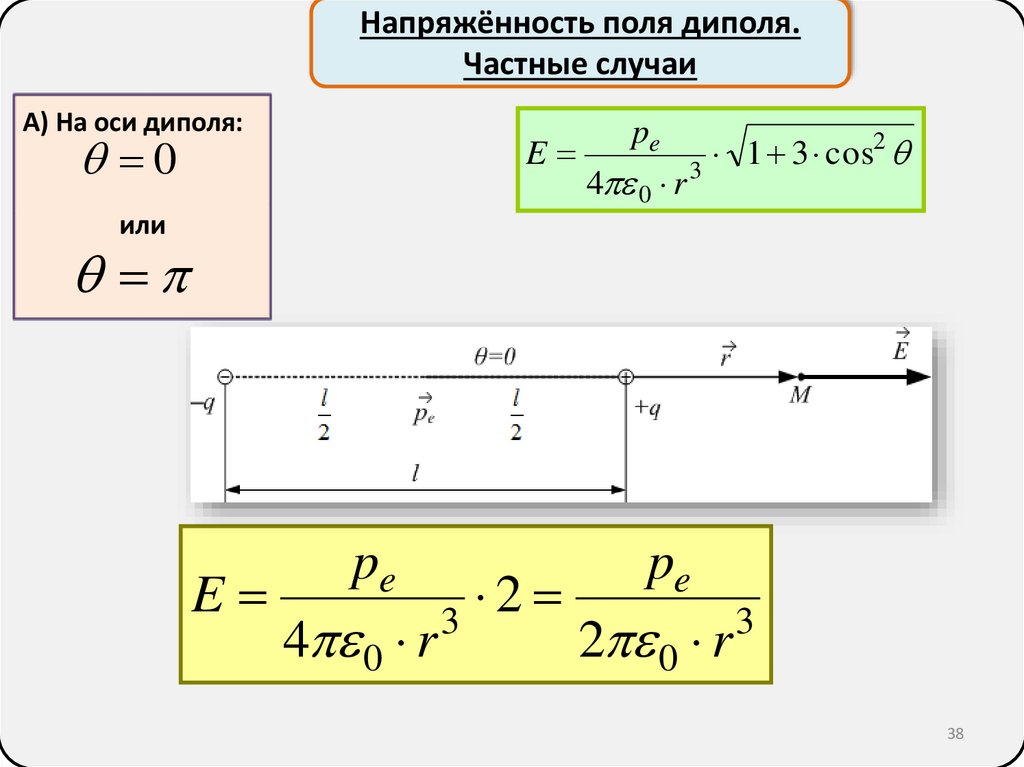
38.

Напряжённость поля диполя.
Частные случаи
А) На оси диполя:
0
E
pe
4 0 r
2
1
3
cos
3
или
pe
pe
E
2
3
3
4 0 r
2 0 r
38

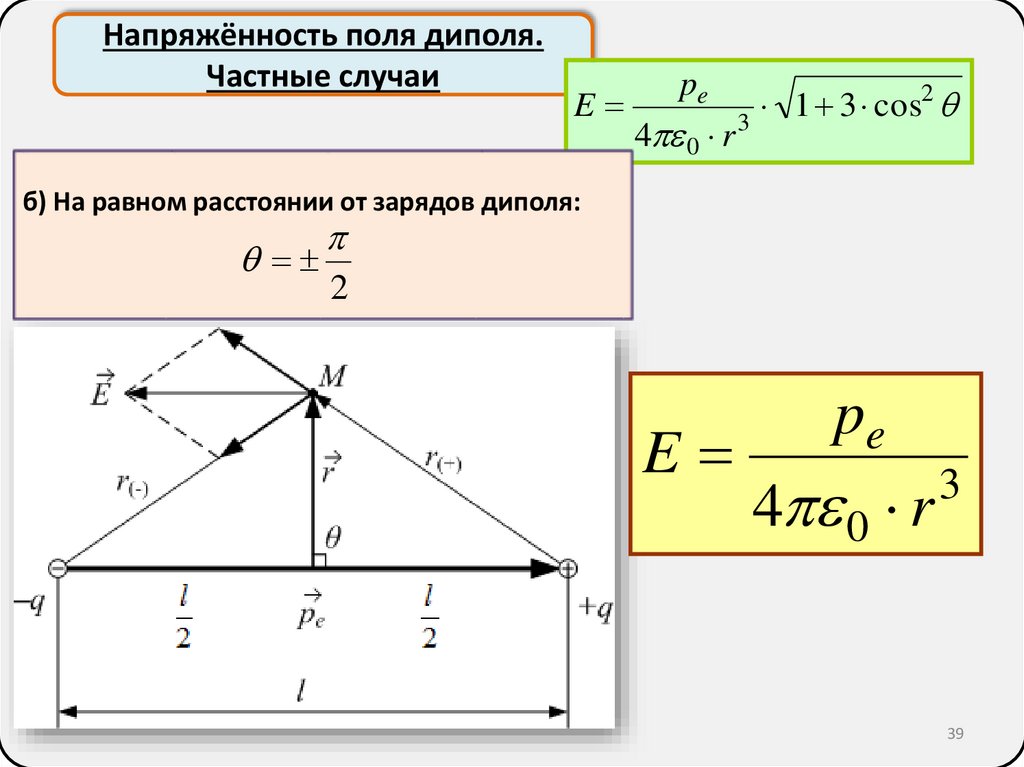
39.

Напряжённость поля диполя.
Частные случаи
E
pe
4 0 r
2
1
3
cos
3
б) На равном расстоянии от зарядов диполя:
2
E
pe
4 0 r
3
39