Похожие презентации:
Циркуляция вектора напряженности электростатического поля. Лекция 2
1. ЛЕКЦИЯ 2
2. ЦИРКУЛЯЦИЯ ВЕКТОРА НАПРЯЖЕННОСТИ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
3.
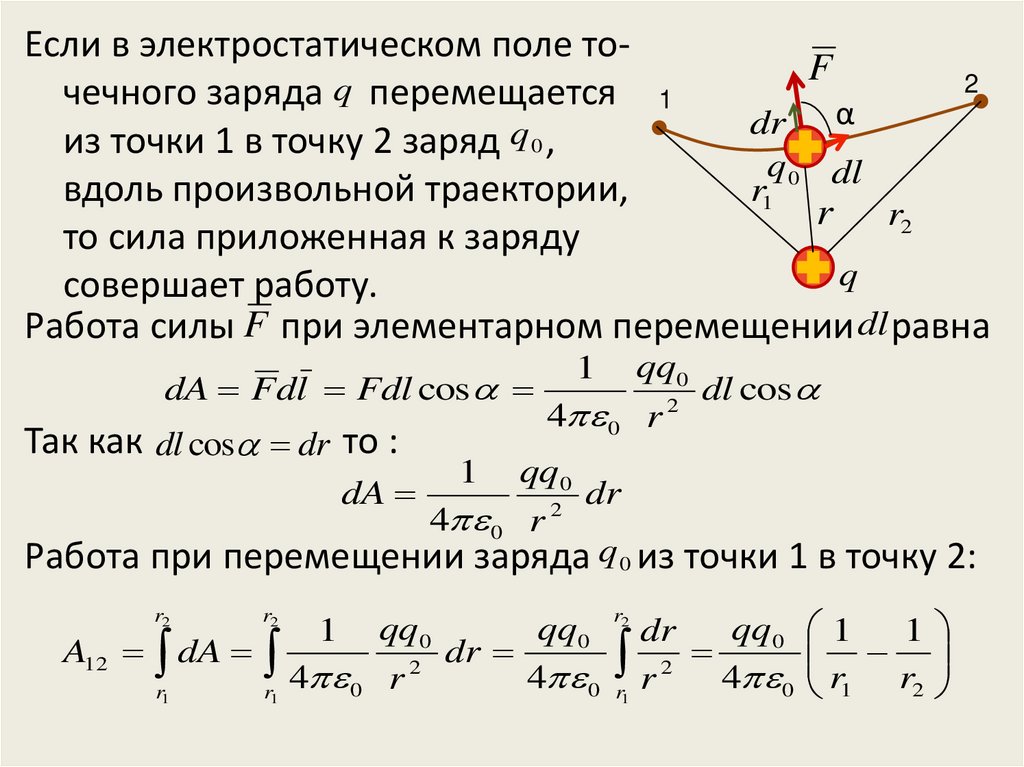
Если в электростатическом поле тоF2
q
чечного заряда перемещается 1
dr α
q
из точки 1 в точку 2 заряд 0 ,
q 0 dl
вдоль произвольной траектории,
r1
r r2
то сила приложенная к заряду
q
совершает работу.
Работа силы F при элементарном перемещении dl равна
qq0
dA Fdl Fdl cos
dl cos
2
4 0 r
Так как dl cos dr то :
1 qq 0
dA
dr
2
4 0 r
Работа при перемещении заряда q 0 из точки 1 в точку 2:
1
qq 0
qq 0 2 dr
qq 0 1
1
A12 dA
dr
2
2
4 0 r
4 0 r1 r
4 0 r1 r2
r1
r1
r2
r2
1
r
4.
Работа А не зависит от траектории перемещения, а определяется только положениями начальной и конечной точек. Значит электростатическое поле точечногозаряда является потенциальным, а электростатические силы – консервативными.
Работа А совершаемая при перемещении электрического заряда во внешнем электростатическом поле по
любому замкнутому пути L равна нулю.
dA 0
Если в качестве заряда переносимого в электростатическое поле взять единичный точечный заряд, то элементарная работа сил поля на пути dl равна
E dl El dl E cos dl
Где El E cos - проекция вектора E на направление
элементарного перемещения.
5.
dA E dl E dl 0L
Интеграл E dl E L dl - циркуляция вектора напряженL
L
L
L
ности. L
Циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю.
Силовое поле, обладающее этим свойством называется потенциальным.
Из обращения в 0 циркуляции вектора E , следует, что
линии напряженности электростатического поля НЕ
МОГУТ БЫТЬ ЗАМКНУТЫМИ. Они начинаются и заканчиваются на положительных и отрицательных зарядах
соответственно, или уходят в бесконечность.
Эта формула справедлива только для электростатического поля, для поля движущихся зарядов, условие E dl 0
L
не выполняется.
6. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
7.
Тело находящееся в потенциальном поле сил, обладаетпотенциальной энергией, за счет которой силами поля
совершается работа. Работа консервативных сил поля
совершается за счет убыли потенциальной энергии.
Поэтому работу сил электростатического поля можно
представить как разность потенциальных энергий, которыми обладает точечный заряд q 0 в начальной и конечной точках поля заряда q .
qq0 1
qq0 1
qq0 1
1
A12
Wп 1 Wп 2
4 0 r1 r2 4 0 r1 4 0 r2
Отсюда получается, что потенциальная энергия заряда
qq0
Wп
С
4 0 r
1
При удалении заряда в бесконечность ( r ), потенциальная энергия превращается в нуль (Wп 0), значит
8.
С 0 , и потенциальная энергия W п заряда q 0 находящегося в электростатическом поле, создаваемом зарядом qна расстоянии r от него будет равна:
qq0
kqq0
Wп
4 0 r
r
1
Для одноименных зарядов произведение qq0 0 и потенциальная энергия их взаимодействия положительна
(отталкивание), для разноименных зарядов qq0 0 и
потенциальная энергия их взаимодействия отрицательна (притяжение).
Если поле создается системой n точечных зарядовq1 , q2 ,...qn,
то, работа электростатических сил, совершаемая над
зарядом q 0 равна алгебраической сумме работ сил обусловленных каждым зарядом по отдельности.
9.
Потенциальная энергия W п зарядаq 0 находящегося в этомполе, равна сумме его потенциальных энергийWni создаваемых каждым из зарядов в отдельности.
n
n
qi
Wп Wni q0
i 1
i 1 4 0 ri
1
Отношение Wп q 0 не зависит от q 0 и является энергетической характеристикой электростатического поля и
называется ПОТЕНЦИАЛ – ϕ.
Wп
q
Потенциал в какой либо точке электростатического поля
это физическая величина определяемая потенциальной энергией единичного положительного заряда помещаемого в данную точку.
10.
Потенциал поля создаваемого точечным зарядом равен1
q
4 0 r
Если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической
сумме потенциалов полей всех этих зарядов.
n
n
qi
i
4
i 1
0 i 1 ri
1
Работа совершаемая силами электростатического поля
при перемещении заряда из точки 1 в точку 2 может
быть представлена как
A12 Wп1 Wп 2 q0 1 2 q0
Работа равна произведению перемещаемого заряда на
разность потенциалов в начальной и конечной точках.
11. РАЗНОСТЬ ПОТЕНЦИАЛОВ
Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля при перемещении единичного положительного заряда из точки 1 в точку 2.2
2
2
1
1
1
A12 q 0 E dl 1 2 E dl El dl
Интегрирование можно проводить вдоль любой линии
соединяющей начальную и конечную точки, так как
здесь работа не зависит от траектории.
Если перемещать заряд из произвольной точки за пределы поля (в бесконечность), где потенциал равен нулю 0 , то работа сил электростатического поля :
A q0
12. ПОТЕНЦИАЛ
ПОТЕНЦИАЛ – физическая величина, определяемая работой по перемещению единичного положительногозаряда при удалении его из данной точки в бесконечность.
A
q0
Эта работа численно равна работе совершаемой внешними силами (против сил электростатического поля),
по перемещению единичного положительного заряда
из бесконечности в данную точку.
Единица потенциала : вольт.
1 вольт – потенциал такой точки поля в которой заряд в
1 Кл обладает потенциальной энергией 1 Дж.
1 В=1 Дж/Кл
13. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ ВЗАИМОСВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ И ПОТЕНЦИАЛОМ
14. ВЗАИМОСВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ И ПОТЕНЦИАЛОМ
• Напряженность Е – СИЛОВАЯ характеристика электростатического поля• Потенциал ϕ – ЭНЕРГЕТИЧЕСКАЯ характеристика электростатического поля
Найдём взаимосвязь между характеристиками электростатического поля.
Работа по перемещению единичного положительного
заряда вдоль оси х , если точки расположены бесконечно близко друг к другу и x2 x1 dx ,будет равна E x dx,
та же работа равна 2 1 .
A E x x
15.
Exx
Где: -символ частной производной, показывает, что
дифференцирование производится только по х.
Повторим аналогичные рассуждения для осей y и z
можно найти вектор E в трёхмерном пространстве.
E
i
j
k grad
y
z
x
Где i , j, k - орты, (единичные векторы осей x,y,z) .
Напряженность электростатического поля равна градиенту потенциала, взятому со знаком минус.
Градиент потенциала: i j k grad
x
y
z
Знак – определяется тем, что вектор напряженности
электростатического поля E направлен в сторону убывания потенциала.
16. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ
Для графического изображения распредеϕ₁ления потенциала электростатического
ϕ₂
q
поля используют эквипотенциальные
поверхности – поверхности, во всех точках которых, потенциал ϕ имеет одно и
тоже значение.
Если поле создается точечным зарядом, то в этом случае
эквипотенциальные поверхности являются концентрическими сферами.
Линии напряженности – радиальные прямые. Следовательно, линии напряженности в случае точечного заряда перпендикулярны эквипотенциальным поверхностям.
17.
Линии напряженности всегда нормальны к эквипотенциальным поверхностям.Все точки эквипотенциальной поверхности имеют одинаковый потенциал, и работа по перемещению заряда вдоль этой поверхности равна нулю.
A12 q0 1 2 q0 ( ) 0
Значит, электростатические силы, действующие на заряд, всегда направлены по нормали к эквипотенциальным поверхностям. Следовательно, вектор E всегда нормален к эквипотенциальной поверхности, а
поэтому линии вектора E ортогональны этим поверхностям.
18. ВЫЧИСЛЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ ПО НАПРЯЖЕННОСТИ ПОЛЯ
19. 1. ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОЙ БЕСКОНЕЧНОЙ ПЛОСКОСТИ
Напряженность данного поля определяется формулой:E
2 0
ϬS
Тогда разность потенциалов в точках 1 и 2 :
x2 x1
1 2 Edx
dx
2 0
2 0
x
x
x2
x2
1
1
Ϭ
x₁
x₂
S
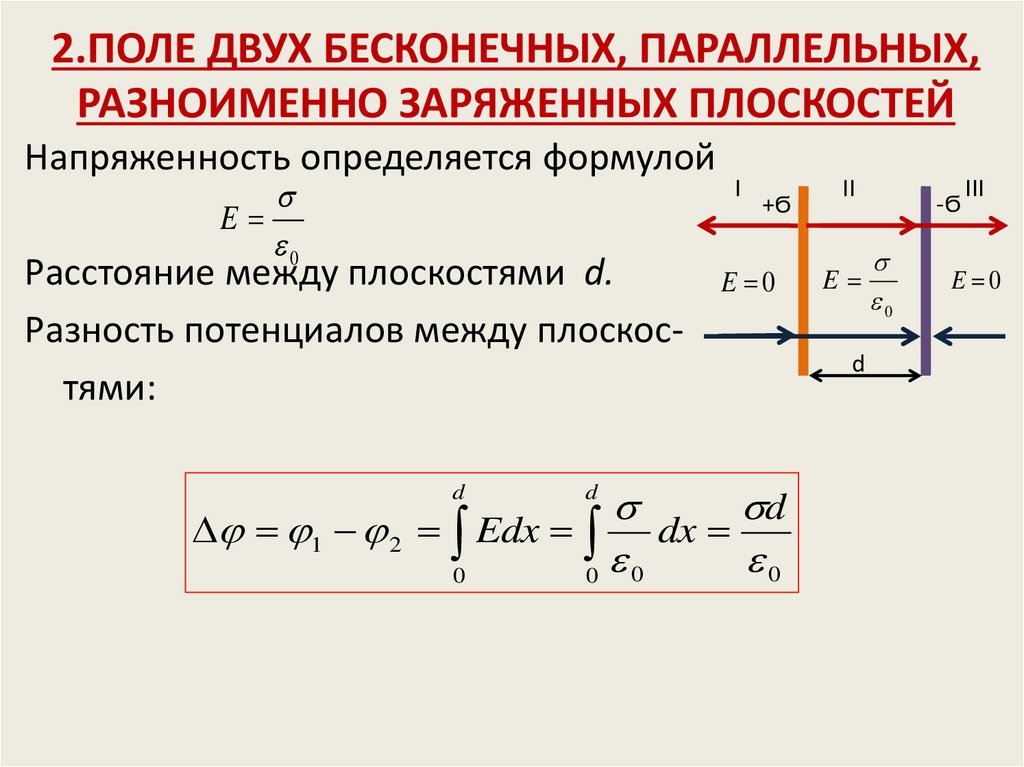
20. 2.ПОЛЕ ДВУХ БЕСКОНЕЧНЫХ, ПАРАЛЛЕЛЬНЫХ, РАЗНОИМЕННО ЗАРЯЖЕННЫХ ПЛОСКОСТЕЙ
Напряженность определяется формулойE
0
Расстояние между плоскостями d.
Разность потенциалов между плоскостями:
І
+Ϭ
E 0
d
1 2 Edx
dx
0
0
0
0
d
d
ІІ
E
d
-Ϭ
0
ІІІ
E 0
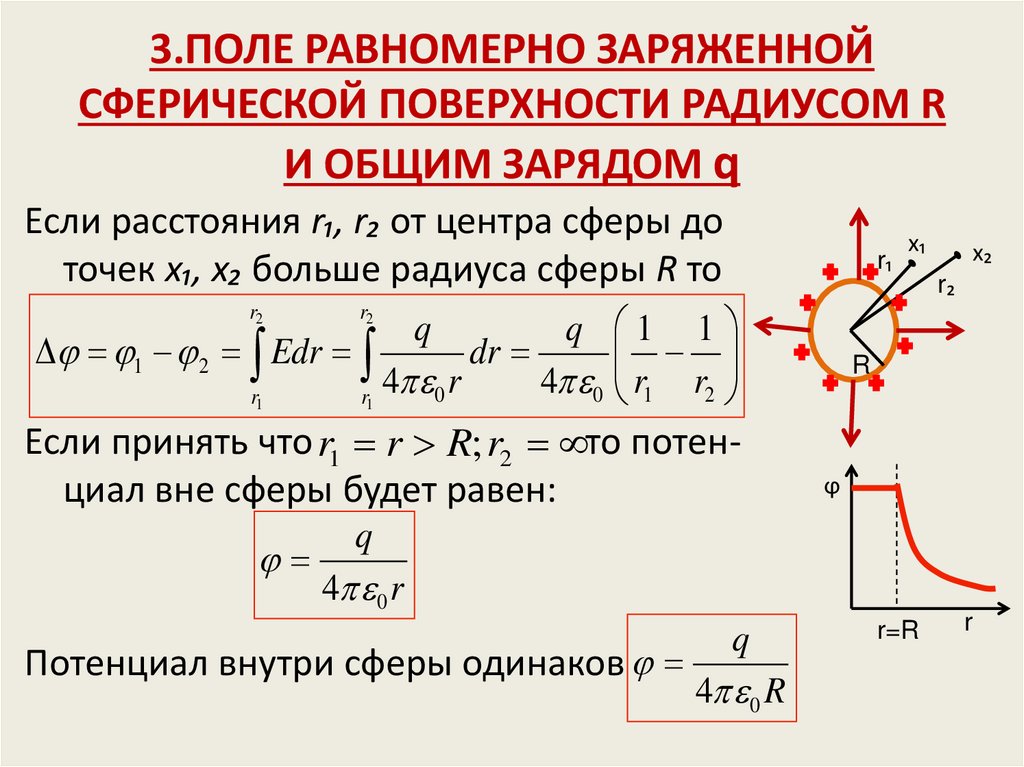
21. 3.ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОЙ СФЕРИЧЕСКОЙ ПОВЕРХНОСТИ РАДИУСОМ R И ОБЩИМ ЗАРЯДОМ q
Если расстояния r₁, r₂ от центра сферы доточек х₁, х₂ больше радиуса сферы R то
r₁
x₂
r₂
q
q 1 1
1 2 Edr
dr
4 0 r
4 0 r1 r2
r1
r1
r2
x₁
r2
Если принять что r1 r R;r2 то потенциал вне сферы будет равен:
R
ϕ
q
4 0 r
q
Потенциал внутри сферы одинаков
4 0 R
r=R
r
22. 4.ПОЛЕ ОБЪЕМНО ЗАРЯЖЕННОГО ШАРА РАДИУСА R, С ОБЩИМ ЗАРЯДОМ q
Вне шара разность потенциалов определяетсяаналогично предыдущему случаю:
q 1 1
1 2
4 0 r1 r2
r'₁
q
r'₂
R
Внутри шара (r'<R) напряженность будет равна:
E
1 q
r
3
4 0 R
Разность потенциалов для точек внутри шара:
r2
r2
qr
q
2
2
1 2 Edr
dr
r
r
1
3
3 2
4 0 R
8 0 R
r1
r
1
r₁
r₂
23. 5. ПОЛЕ РАВНОМЕРНО ЗАРЯЖЕННОГО БЕСКОНЕЧНОГО ЦИЛИНДРА РАДИУСА R C ЛИНЕЙНОЙ ПЛОТНОСТЬЮ τ
Вне цилиндра (r>R) напряженность равна1
E
2 0 r
R
r₁
Следовательно, разность потенциалов:
r2
dr
1 2 Edr
ln
2 0 r r 2 0 r1
r
r2
r2
1
1
r₂
24. ВЕЩЕСТВО В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
25. ДИЭЛЕКТРИК В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКА
26.
Диэлектрики – вещества, при обычных условиях не проводящие электрический ток.Все молекулы и атомы диэлектрика электрически нейтральны (положительный заряд ядра атома равен отрицательному заряду электронов атома и суммарный
заряд атома равен нулю). Однако молекулы обладают
электрическими свойствами.
Если заменить положительный заряд ядер атомов молекул суммарным зарядом +q ,а заряд всех электронов суммарным отрицательным зарядом –q, находящемся в «центре тяжести» отрицательных зарядов, то
молекулу можно рассматривать как электрический
диполь с электрическим моментом p ql ( q-суммарный положительный заряд ядер, l -вектор проведенный из «центра тяжести» электронов к протонам.
27.
В диэлектриках нет свободных носителей заряда (заряженных частиц, которые могли бы прийти под воздействием электрического поля в упорядоченное движение и организовать электрический ток.Диэлектриками являются:
• Все газы (если они не подверглись ионизации)
• Некоторые жидкости (дистиллированная вода, бензол
и масла (нефтяные и растительные)
• Твердые тела (стекло, фарфор, слюда и т.п.)
Удельное электрическое сопротивление диэлектриков
10 6 1015 Ом*м, ( у металлов 10 8 10 6 Ом*м).
28. ТИПЫ ДИЭЛЕКТРИКОВ
29. ПЕРВАЯ ГРУППА
(N₂, H₂, O₂, CO₂…) – вещества молекулы которых имеютсимметричное строение, то есть «центры тяжести»
положительных и отрицательных зарядов в отсутствие внешнего электрического поля совпадают и
дипольный момент молекулы равен нулю р 0 .
Молекулы таких диэлектриков называют неполярными. Под действием внешнего электрического поля заряды неполярных молекул смещаются в противоположные стороны (положительные по полю, отрицательные против) и молекула приобретает дипольный
момент.
30. ВТОРАЯ ГРУППА
(H₂O, NH₃, SO₂ CO…) – вещества молекулы которых имеют асимметричное строение , то есть «центры тяжести» положительных и отрицательных зарядов не совпадают. Эти молекулы и в отсутствие внешнего электрического поля обладают дипольным моментом. Молекулы таких диэлектриков называются полярными.При отсутствии внешнего электрического поля, дипольные моменты полярных молекул вследствие теплового движения ориентированы хаотично и их результирующий момент равен нулю. Если такой диэлектрик поместить во внешнее электрическое поле, то
силы этого поля будут стремиться повернуть диполи
вдоль поля, и возникает, отличный от нуля, электрический момент.
31. ТРЕТЬЯ ГРУППА
(NₐCL, KCL) – Вещества, молекулы которых имеют ионноестроение. Ионные кристаллы представляют собой пространственные решетки с правильным чередованием
ионов различных знаков. В этих кристаллах нельзя выделять отдельные молекулы, и рассматривать их можно как систему двух вдвинутых одна в другую ионных
подрешеток. При наложении на ионный кристалл электрического поля происходит некоторая деформация
кристаллической решетки или относительное смещение подрешеток, приводящее к возникновению
дипольных моментов.
32. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ ТИПЫ ПОЛЯРИЗАЦИИ ПОЛЯРИЗОВАННОСТЬ
33.
Внесение всех трёх групп диэлектриков во внешнее электростатическое поле приводит к возникновению отличного от нуля результирующего момента диэлектрика, или иначе к ПОЛЯРИЗАЦИИ ДИЭЛЕКТРИКА.ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКА – процесс ориентации диполей или появления под воздействием электрического поля ориентированных по полю диполей.
В зависимости от строения молекул (атомов) диэлектрика (соответственно 3 группам диэлектриков) различают 3 типа поляризации:
1. Электронная поляризация
2. Ориентационная поляризация
3. Ионная поляризация
34. 1. Электронная (деформационная) поляризация
Осуществляется у неполярных диэлектриков. Под действием внешнего электрического поля возникают наведенные (индуцированные) дипольные моментынаправленные вдоль поля,(по направлению E ). Тепловое движение молекул не влияет на электронную
поляризацию. В газообразных и жидких полярных
диэлектриках происходит одновременно с ориентационной.
35. 2. Ориентационная поляризация
Наблюдается у полярных диэлектриков. Внешнее электрическое поле стремится ориентировать дипольныемоменты полярных молекул-диполей по направлению вектора E . Этому препятствует хаотическое движение молекул, вызывающее беспорядочный разброс диполей. В итоге совместного действия электрического поля и теплового движения, возникает преимущественная ориентация дипольных электрических
моментов вдоль поля, возрастающая с увеличением
напряженности электрического поля, и с уменьшением температуры.
36. 3. Ионная поляризация
Возникает в твердых диэлектриках имеющих ионнуюкристаллическую решетку. Внешнее электрическое
поле вызывает в таких диэлектриках смещение всех
положительных ионов в направлении напряженности поля E , а всех отрицательных ионов в противоположную сторону. Происходит смещение подрешеток
приводящее к возникновению дипольных моментов.
37. ПОЛЯРИЗОВАННОСТЬ
При помещении диэлектрика во внешнее электростатическое поле он поляризуется, то есть приобретаетотличный от нуля дипольный момент pV pi
i
p i - дипольный момент одной молекулы.
Количественной мерой поляризации служит:
Поляризованность (вектор поляризации) Р - дипольный
момент единицы объема диэлектрика.
pV
P
V
p
i
i
V
В пределах малого объема все молекулы неполярного
диэлектрика приобретают в электрическом поле оди-
38.
наковые индуцированные электрические моменты p i .Поляризованность неполярного диэлектрика равна:
Np
P
np
V
n N V - концентрация молекул.
Принято считать что поляризованность P линейно зависит от напряженности поля E . Если E не очень велико то:
P 0 Е
- диэлектрическая восприимчивость вещества
( 0)
- безразмерная величина
характеризующая
свойства диэлектрика ( значение для диэлектриков
обычно несколько единиц, но бывает и выше (для воды 80 ,для спирта 25 )).
39.
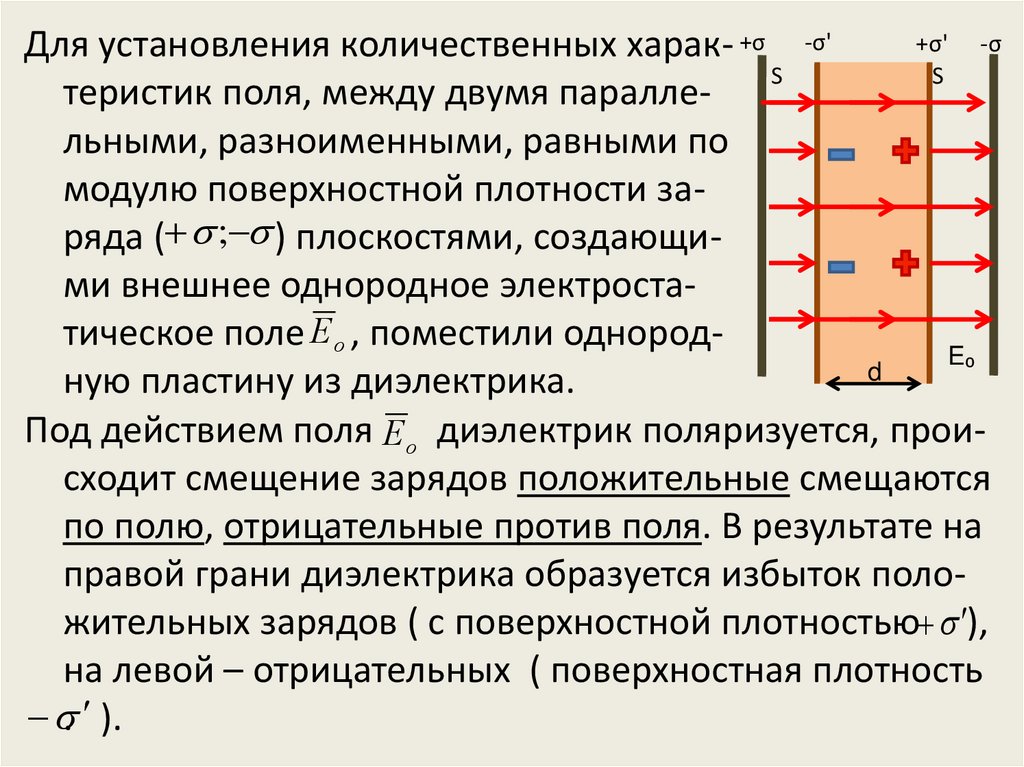
+σ' -σДля установления количественных харак- +σ -σ'
S
S
теристик поля, между двумя параллельными, разноименными, равными по
модулю поверхностной плотности заряда ( ; ) плоскостями, создающими внешнее однородное электростатическое поле Е о , поместили однородE₀
d
ную пластину из диэлектрика.
Под действием поля Е о диэлектрик поляризуется, происходит смещение зарядов положительные смещаются
по полю, отрицательные против поля. В результате на
правой грани диэлектрика образуется избыток положительных зарядов ( с поверхностной плотностью ),
на левой – отрицательных ( поверхностная плотность
. ).
40.
Эти нескомпенсированные заряды, появляющиеся в результате поляризации диэлектрика называются связанными. Так как , то не всё поле Е о компенсируется полем зарядов диэлектрика, часть линий напряженности пройдет сквозь диэлектрик, другая частьобрывается на связанных зарядах. Следовательно,
поляризация диэлектрика вызывает в нём уменьшение поля, по сравнению с первоначальным. Вне
диэлектрика Е Е о .
Появление связанных зарядов приводит к возникновению дополнительного электрического поля Е (вызываемого связанными зарядами), направленного против внешнего поля Е о (созданного свободными зарядами) и ослабляет его.
41. Диэлектрическая проницаемость вещества
Результирующее поле внутри диэлектрика:Е Ео Е
Так как Е создаётся разноименными плоскостями с поверхностной плотностью то
Е 0
Е Ео 0
Определим поверхностную плотность связанных зарядов
Полный дипольный момент пластинки диэлектрика:
pV PV PSd PSd Sd P
p q d Sd
V
- площадь грани пластинки диэлектрика
S
- толщина диэлектрика
d
q S - заряд на каждой грани диэлектрика
42.
PПоверхностная плотность связанных зарядов равна
поляризованности P . Из этого следует:
Е Ео P 0 Ео 0 Ео 0 E 0 Ео E
Напряженность результирующего поля внутри диэлектрика равна:
Е0
Е0
Е
1
1
- диэлектрическая проницаемость, безразмерная величина, показывающая во сколько раз поле ослабляется диэлектриком, характеризует количественное
свойство диэлектрика поляризоваться в электрическом поле.
43. ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ ТЕОРЕМА ОСТРОГРАДСКОГО – ГАУССА ДЛЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ В ДИЭЛЕКТРИКЕ
44. ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ
Напряженность электростатического поля зависит отсвойств среды. В однородной среде Е обратно пропорционально . Вектор E , переходя через границу
диэлектриков, испытывает скачкообразное изменение. Для удобства расчетов, необходимо помимо вектора напряженности охарактеризовать электрическое
поле вектором электрического смещения D .
D 0 Е
1 D Е Р
Р Е
0
0
Единица электрического смещения Кл/м²
45.
Связанные заряды появляются в диэлектрике при наличии внешнего электростатического поля создаваемогосистемой свободных зарядов, то есть в диэлектрике
на электростатическое поле свободных зарядов накладывается дополнительное поле связанных зарядов.
Результирующее поле описывается вектором напряженности E и зависит от свойств диэлектрика.
Вектором D описывается электростатическое поле создаваемое свободными зарядами . Связанные заряды
возникающие в диэлектрике могут, однако, вызвать
перераспределение свободных зарядов создающих
поле. Поэтому D характеризует электростатическое
поле создаваемое свободными зарядами (в вакууме),
но при таком их распределении в пространстве, которое имеется при наличии диэлектрика.
46.
Подобно E , D изображается с помощью линий электрического смещения, направление и густота которыхопределяются так же как и для линий напряженности.
Отличие в том, что линии вектора E могут начинаться и
заканчиваться на любых (свободных и связанных) зарядах, а линии вектора D только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.
47. ТЕОРЕМА ОСТРОГРАДСКОГО – ГАУССА ДЛЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ В ДИЭЛЕКТРИКЕ
Для произвольной замкнутой поверхности S поток вектора электрического смещения Dсквозь эту поверхность равен:D D dS Dn dS
S
S
Теорема Остроградского-Гаусса для электростатического
поля в диэлектрике имеет вид:
n
D dS D dS q
n
i 1
св обi
Поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность
равен алгебраической сумме заключенных внутри этой
поверхности свободных электрических зарядов.
48.
В данной форме теорема Гаусса справедлива для электростатического поля как для однородных , так и длянеоднородных сред.
В случае вакуума (ε=1) выполняется условие Dn 0 En ,
тогда поток вектора напряженности E сквозь произвольную замкнутую поверхность равен
n
E 0 E n dS qi
i 1
Так как источниками поля E в среде являются как свободные, так и связанные заряды, то теорему Гаусса для
поля E в самом общем виде можно записать:
n
E dS E dS q
0
0
n
i 1
k
свобi
q связi
i 1
49.
nq
i 1
n
св обi
, q св язi -соответственно алгебраические суммы
i 1
свободных и связанных зарядов, охватываемых замкнутой поверхностью S.
Данная формула не подходит для описания поля E в диэлектрике, так как она выражает свойства неизвестного
поля E через связанные заряды, которые в свою очередь определяются им же. Это доказывает целесообразность введения вектора D .













































 Физика
Физика








