Кручение

1.

КРУЧЕНИЕ

2.

КРУЧЕНИЕ
Примеры механизмов, воспринимающих крутящие моменты
Распространенным примером являются трансмиссии
Трансмиссия – (transmissio — передача, переход) - устройство для передачи механической энергии от двигателя к
исполнительным органам машины либо к другим рабочим
машинам (станкам, мельницам и т.п.).
Передача вращения от трансмиссионного вала к рабочим
машинам обычно производится приводными ремнями (контрпривод).
В современной технике под Т. понимается вся совокупность
передаточных устройств от вала двигателя до рабочих
органов машины, на которой он установлен.
Так, в автомобиле или тракторе в состав механической Т.
входят Силовая передача, Сцепление, Карданная
передача, Дифференциальный механизм и др. устройства.

3.

КРУЧЕНИЕ
Брусья, передающие крутящий момент называются
валами или осями.
Внешние скручивающие моменты, как правило,
передаются на вал в местах посадки на него
шкивов, зубчатых колес.
В большинстве случаев бывают заданы мощность,
передаваемая валом, и число оборотов, величины
скручивающих моментов определяются исходя из
этих данных.
Те- внешний крутящий момент; N – мощность в кВт;
n – число оборотов в минуту.
По величине приложенных внешних крутящих
моментов Те методом сечений определяются
внутренние крутящие моменты Т

4.

КРУЧЕНИЕ
По величине приложенных внешних крутящих
моментов Те методом сечений определяются
внутренние крутящие моменты Т

5.

Определение напряжений и деформаций при кручении
Т
Ip

6.

Определение напряжений и деформаций при кручении
Максимальные касательные напряжения будут при

7.

Определение напряжений и деформаций при кручении
Введем понятие момента сопротивления – это
отношение момента инерции к расстоянию до
наиболее удаленной точки сечении
Wp
Тогда
Ip
r
T
max
Wp
Полный угол закручивания на длине l

8.

КРУЧЕНИЕ
Расчет валов на прочность и жесткость
Условие прочности при кручении
Условие жесткости при кручении
Tl
мах
adm
I pG

9.

Расчет валов на прочность и жесткость
Полярный момент инерции круга
Момент сопротивления
Исходя из условия прочности и формул для
моментов, можно рассчитать вал на прочность и
жесткость.

10.

Расчет валов на прочность и жесткость
После подстановки получим
диаметр из условия прочности
и из условия жесткости

11.

Кручение. Пример решения задачи
Задание 2. К стальному валу приложены три известных момента Т1,
Т2, Т3.
1. Определить величину момента Х, если угол закручивания правого
торцевого сечения вала равен нулю.
2. Построить эпюру крутящих моментов.
3. При заданном значении adm определить диаметр вала из расчета
на прочность и округлить его значение до ближайшего равного: 30,
35, 40, 45, 50, 60, 70, 80,90, 100 мм.
4. Построить эпюру углов закручивания, найти наибольший
относительный угол закручивания и проверить вал на жесткость при
φadm = 1,5 град/м. G=8·104 МПа
е
е
е
Т
Х
Т1
Т2
3
а
b
c
а

12.

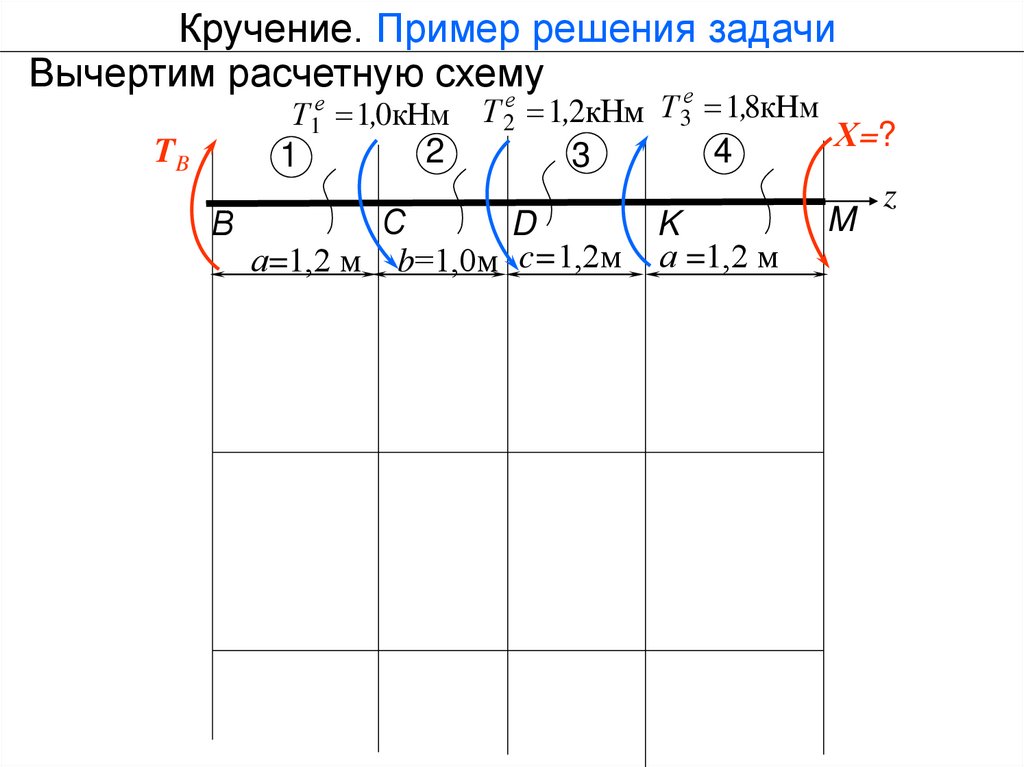
Кручение. Пример решения задачи
Вычертим расчетную схему
е
е
Т1е 1,0кНм Т 2 1,2кНм Т 3 1,8кНм
TB
1
В
2
3
С
D
а=1,2 м b=1,0м c=1,2м
4
K
а =1,2 м
Х=?
M
z

13.

Кручение. Пример решения задачи
Как можно видеть по расчетной схеме, в задаче 2 неизвестных величины: ТВ-реактивный момент
в заделке, Х-определяемый момент, т. е задача
статически неопределима, так как из уравнения
статики их определить
не
удастся
е
е
е
Т1
TB
1
В
Т3
Т2
2
3
С
D
а=1,2 м b=1,0м c=1,2м
4
K
а =1,2 м
ΣМz= - X+T3 –T2 – T1+ TB =0
TB= X - T3 +T2 + T1
Х=?
M
z

14.

Кручение. Пример решения задачи
В качестве второго уравнения используем условие
задачи.
Угол закручивания правого концевого сечения
выразим алгебраической суммой взаимных углов
закручивания сечений отдельных участков под
действием каждого из крутящих моментов в
отдельности:
Tl
I pG

15.

Кручение. Пример решения задачи
Т 1е
TB
1
В
2
Т 2е
3
С
D
а=1,2 м b=1,0м c=1,2м
Т 3е
4
K
а =1,2 м
Х=?
M
z
Разобьем вал на участки и запишем выражения
для внутренних усилий
l1= a;
l2=b;
l3= c;
l4= a;

16.

Кручение. Пример решения задачи
Подставим значение реактивного момента в
формулы крутящих моментов:
Тогда угол закручивания в сечении М
( Х Т 3е Т 2е Т1е )а ( Х Т 3е Т 2е )b ( Х Т 3е )с Ха
0
I pG
I pG
I pG
I pG

17.

Кручение. Пример решения задачи
После открытия скобок и преобразования получаем
е
е
е
Х ( 2а b c ) Т 3 ( а b c ) Т 2 ( а b) Т 1 а
GI p
0
е
е
е
Х ( 2а b c ) Т 3 ( а b c ) Т 2 ( а b ) Т1 а 0
откуда
Т 3е ( а b c ) Т 2е ( а b ) Т1е а
Х
2а b c
1800 (1,2 1 1,2) 1200 (1,2 1) 1000 1,2
Х
496 Н
2 1,2 1 1,2

18.

Кручение. Пример решения задачи
Определим значения крутящих моментов
Т1 496 1800 1200 1000 896 Н
Т 2 496 1800 1200 104 Н
Т 3 496 1800 1304 Н
Т 4 496 Н
и построим эпюру крутящих моментов

19.

Кручение. Пример решения задачи
е
Т 2е 1,2кНм Т 3 1,8кНм
Х=?
TB
2
4
1
3
z
M
С
В
D
K
а=1,2 м b=1,0м c=1,2м а =1,2 м
Т1е 1,0кНм
896
Т, Нм
496
104
1304
0,0219
0,0198
α, рад
0,0121

20.

Кручение. Пример решения задачи
Определим диаметр из условия прочности
16 1304
d 3
0
,
048
м
48
мм
3,14 60 10 6
Округляем диаметр до 50 мм и определяем углы
закручивания на участках, предварительно
рассчитав жесткость вала
d
10 3.14 0.05
2
G Ip G
8 10
49603 Нм
32
32
4
4

21.

Кручение. Пример решения задачи
Tl
I pG
896 1,2
104 1,0
1
0,0219 рад 2
0,0021рад
49063
49063
496 1,2
1304 1,2
0,0121рад
3
0,0319 рад 4
49063
49063
Определим угловые перемещения в сечениях по
длине вала
αВ=0; αС= αВ+φ1=0,0219 рад;
αD= αС +φ2=0,0219-0,0021= 0,0198рад;
αК= αD +φ3=0,0198-0,0319= -0,0121рад;
αМ= αК +φ4= -0,0121+0,0121=0;
Строим эпюру углов поворота по длине вала.

22.

Кручение. Пример решения задачи
е
Т 2е 1,2кНм Т 3 1,8кНм
Х=?
TB
2
4
1
3
z
M
С
В
D
K
а=1,2 м b=1,0м c=1,2м а =1,2 м
Т1е 1,0кНм
896
Т, Нм
496
104
1304
0,0219
0,0198
α, рад
0,0121

23.

Кручение. Пример решения задачи
Определим относительный угол закручивания на
каждом участке
i
i
li
0,0219
1
0,0182 рад/м
1,2
0,0021
2
0,0021рад/м
1,0
0 ,0319
3
0 ,0265 рад/м
1,2
0 ,0121
4
0 ,0100 рад/м
1,2

24.

Кручение. Пример решения задачи
Проверим вал по условию жесткости
Tl
мах
adm
I pG
Наибольшим является относительный угол закручивания на 3 участке
Переведем значение из радиан в градусы
180
3 0,0265
1,51 град/м >1,5
Проверим величину превышения
1,51 1,5
100 % 0 ,7%
1,5
Можно принять диаметр вала 50 мм, т.к.отклонение
до 5% считается допустимым