Похожие презентации:
Матрицы и определители
1.
Матрицы иопределители
2.
1.2.
Цели и задачи:
Изучение теоретического материала
по теме: Матрицы. Операции с
матрицами. Определитель.
Формирование
практических
навыков при решении задач по
данной теме.
3.
Матрицы встречаются почти во всехотраслях человеческой деятельности.
Они используются в математике, в
физике, в технике, в экономике, в теории
управления и статистики, других
областях науки и знаний.
4.
Матрицей размера m n называетсяпрямоугольная таблица чисел, содержащая
m строк и n столбцов, и обозначается:
a11 a12
a 21 a 22
...
...
Аm n
ai1 ai 2
...
...
a
am2
m1
...
...
...
...
...
...
a1 j
a2 j
...
aij
...
a mj
...
...
...
...
...
...
a1n
a2n
...
ain
...
a mn
5.
a ij - элементы матрицы,где i – номер строки,
j – номер столбца.
6.
Матрица, состоящая из одной строкиназывается вектор-строкой, а матрица,
состоящая из одного столбца — векторстолбцом.
b11
b21
В ... , А a11
bm1
a12 ... a1n
7.
С помощью матриц удобно записывать некоторыеэкономические зависимости.
Например, рассмотрим таблицу распределения
ресурсов по отдельным отраслям экономики (усл.
ед.):
Ресурсы
Отрасли экономики
Промышленность
Сельское хозяйство
Электроэнергия
5,3
4,1
Трудовые ресурсы
2,8
2,1
Водные ресурсы
4,8
5,1
8.
Данная таблица может быть записана вкомпактной форме в виде матрицы
распределения ресурсов по отраслям:
5,3
А= 2,8
4,8
4,1
2,1
5,1
9.
Матрица, все элементы которой равнынулю, называется нуль-матрицей или
нулевой матрицей и обозначается :
0
0
0 m n
...
0
0
0
...
0
...
...
...
...
0
0
.
...
0
10.
Матрица называется квадратной, есличисло ее строк m
равно числу ее
столбцов n.
Диагональ квадратной матрицы, на
которой расположены элементы
а11,
а22,…,ann
называется
главной
диагональю матрицы, а диагональ с
элементами а1n, а2n-1,…,am1 называется
побочной.
11.
Квадратная матрица, у которой всенедиагональные элементы равны нулю,
называется диагональной матрицей
и
обозначается:
a11
0
D 0
...
0
0
a 22
0
...
0
0
0
a33
...
0
... 0
... 0
... 0
... ...
... a nn
12.
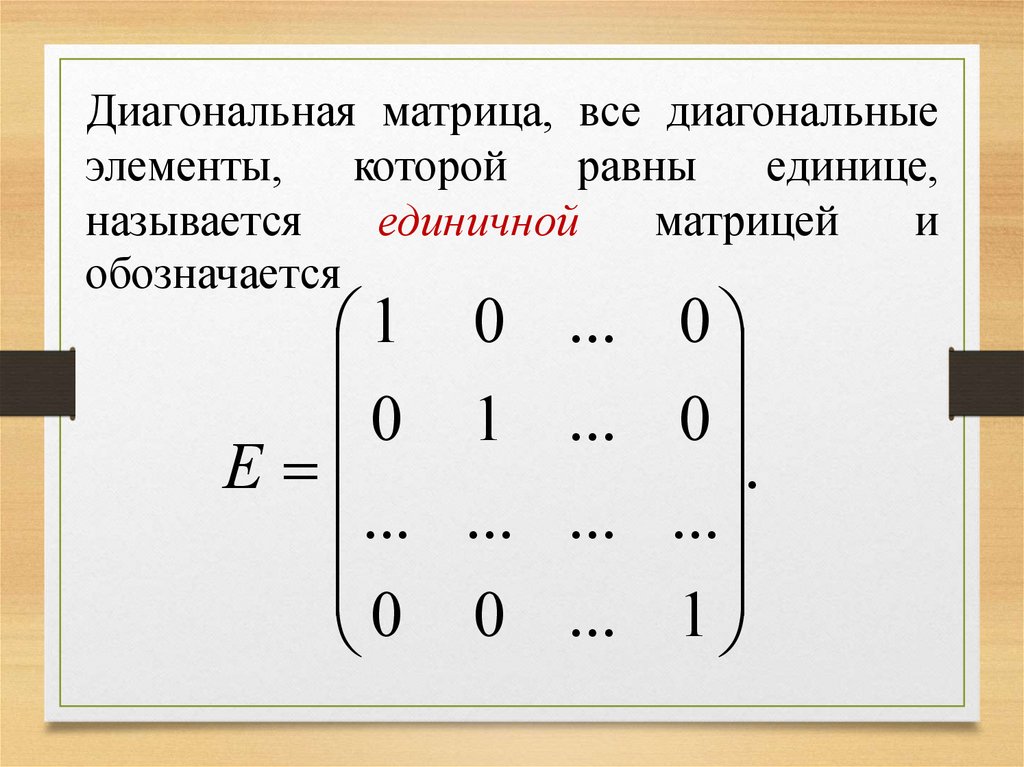
Диагональная матрица, все диагональныеэлементы,
которой
равны
единице,
называется
единичной
матрицей
и
обозначается
1
0
E
...
0
0
1
...
0
...
...
...
...
0
0
.
...
1
13.
Две матрицы одного типа (m n)называются равными, если равны их
соответствующие элементы: aij=bij.
a11
a 21
A a31
...
a
m1
a12
a 22
a32
...
am2
a13
a 23
a33
...
a m3
...
...
...
...
...
a1n
b11
a2n
b21
a3n , B b31
...
...
b
a mn
m1
b12
b22
b32
...
bm 2
b13
b23
b33
...
bm3
...
...
...
...
...
b1n
b2 n
b3n
...
bmn
14.
ОПЕРАЦИИ НАД МАТРИЦАМИ1. Транспонирование матриц.














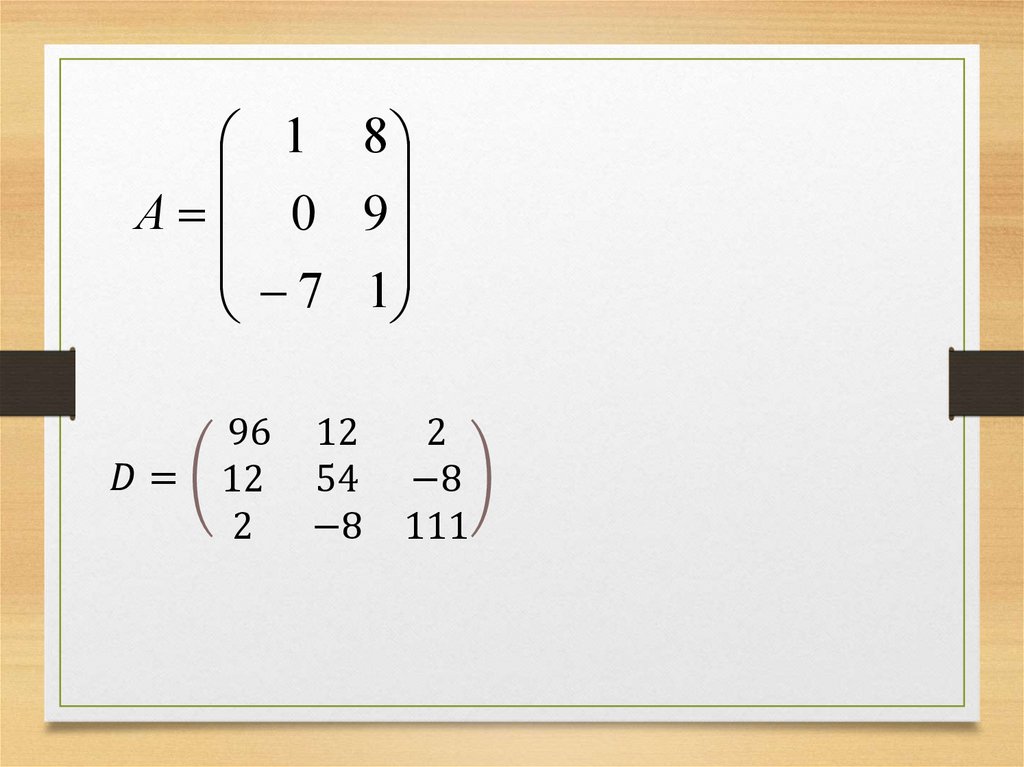


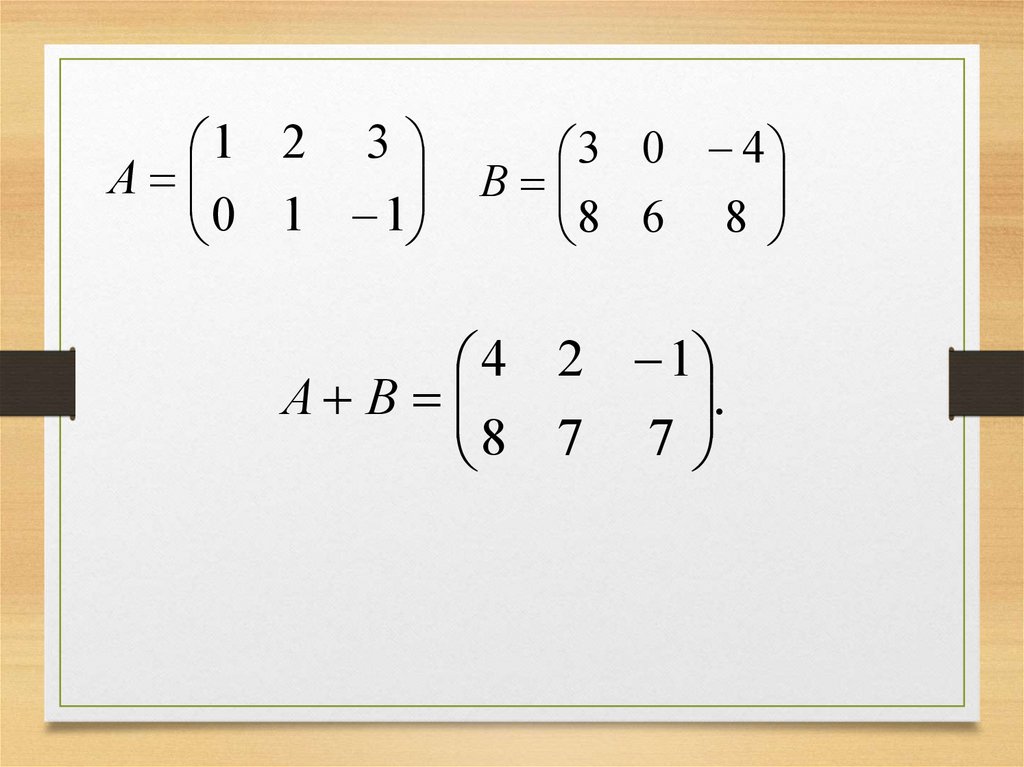












 Математика
Математика








