Поверхностные явления

1.

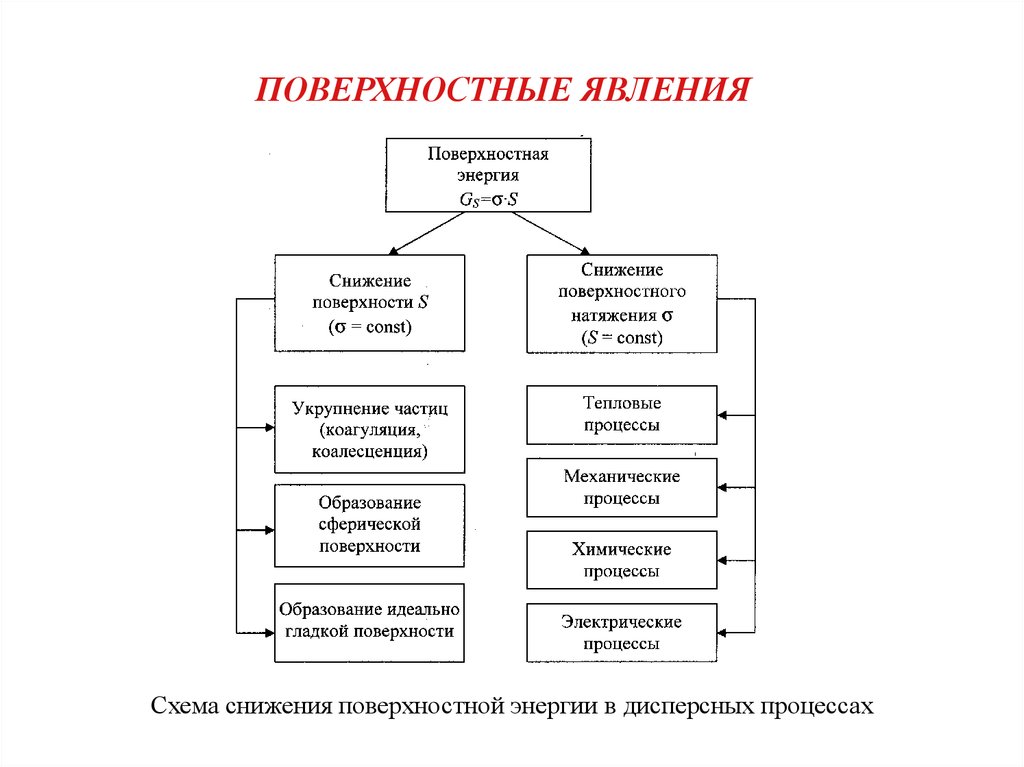
ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
Схема снижения поверхностной энергии в дисперсных процессах

2.

Шар – это форма тела с минимальной
поверхностью и минимальной
поверхностной энергией
Поверхностное натяжение
определяет форму пузырьков газа в
пене

3.

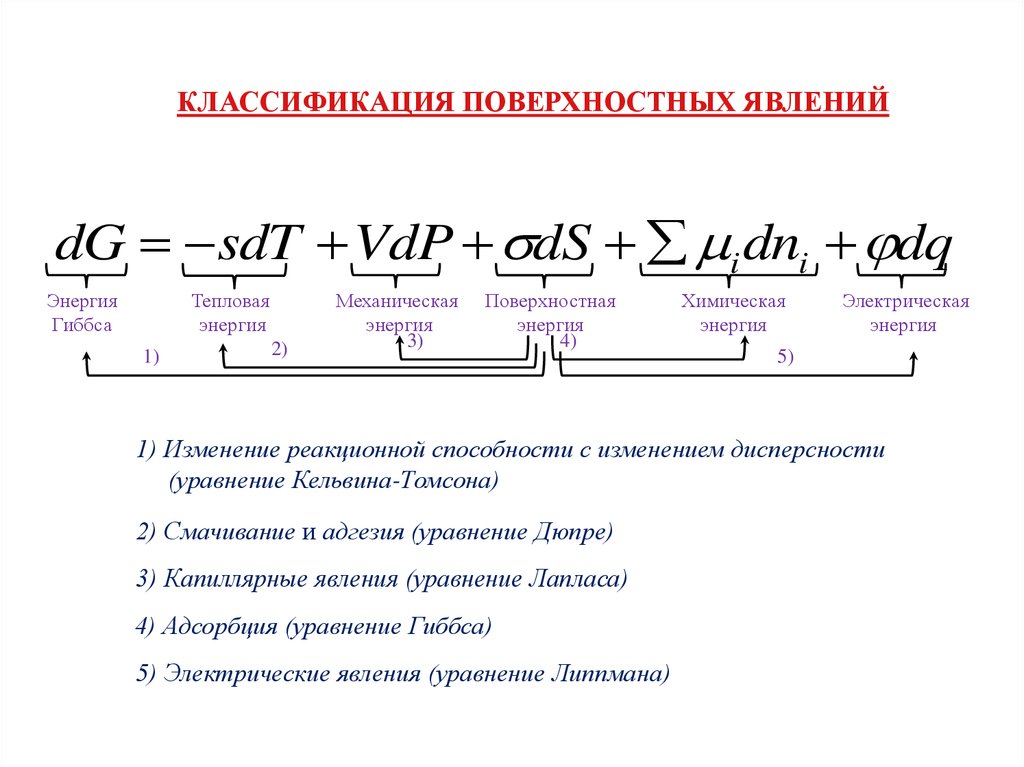
КЛАССИФИКАЦИЯ ПОВЕРХНОСТНЫХ ЯВЛЕНИЙ
dG sdT VdP dS i dni dq
Энергия
Гиббса
Тепловая
энергия
1)
2)
Механическая
энергия
3)
Поверхностная
энергия
4)
Химическая
энергия
Электрическая
энергия
5)
1) Изменение реакционной способности с изменением дисперсности
(уравнение Кельвина-Томсона)
2) Смачивание и адгезия (уравнение Дюпре)
3) Капиллярные явления (уравнение Лапласа)
4) Адсорбция (уравнение Гиббса)
5) Электрические явления (уравнение Липпмана)

4.

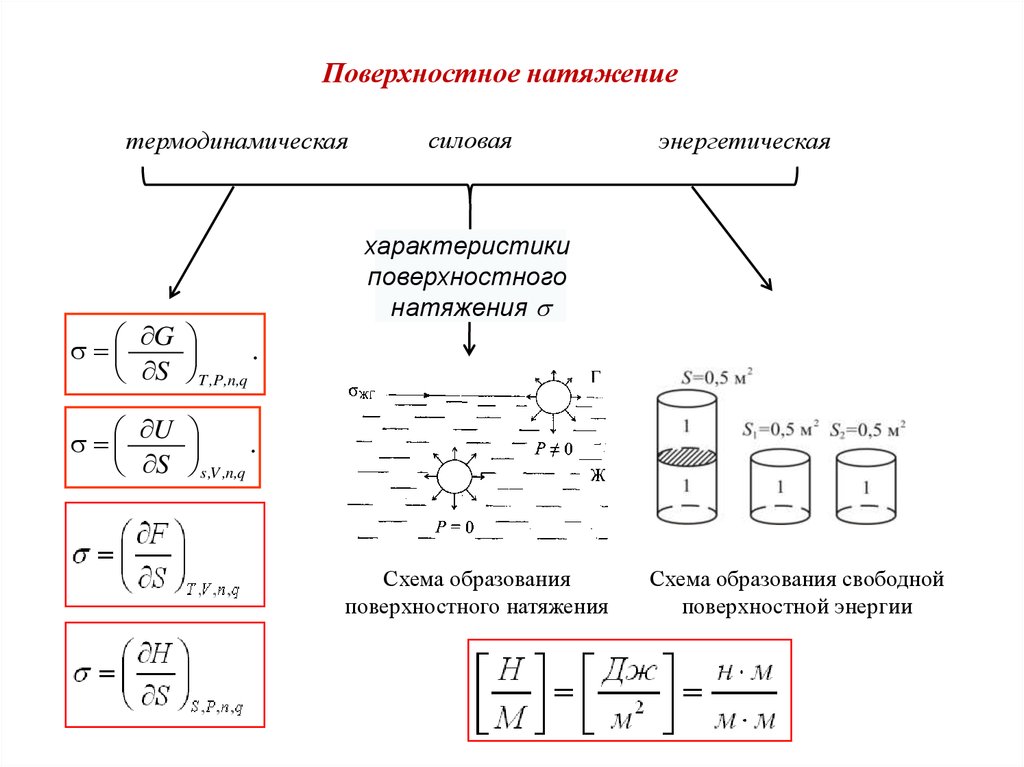
ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
Термодинамическая
характеристика
Поверхностное натяжение – есть частная производная от
энергии Гиббса по величине поверхности раздела фаз при
постоянных значениях температуры, давления, числа молей
компонентов и зарядов.
Силовая
характеристика
Поверхностное натяжение – это сила, отнесенная к
единице длины контура, ограничивающего данную
поверхность.
Энергетическая
характеристика
Поверхностное натяжение – это удельная
свободная поверхностная энергия.

5.

Поверхностное натяжение
термодинамическая
G
.
S
T ,P,n,q
силовая
энергетическая
характеристики
поверхностного
натяжения
U
.
S s,V ,n,q
Схема образования
поверхностного натяжения
Схема образования свободной
поверхностной энергии

6.

7.

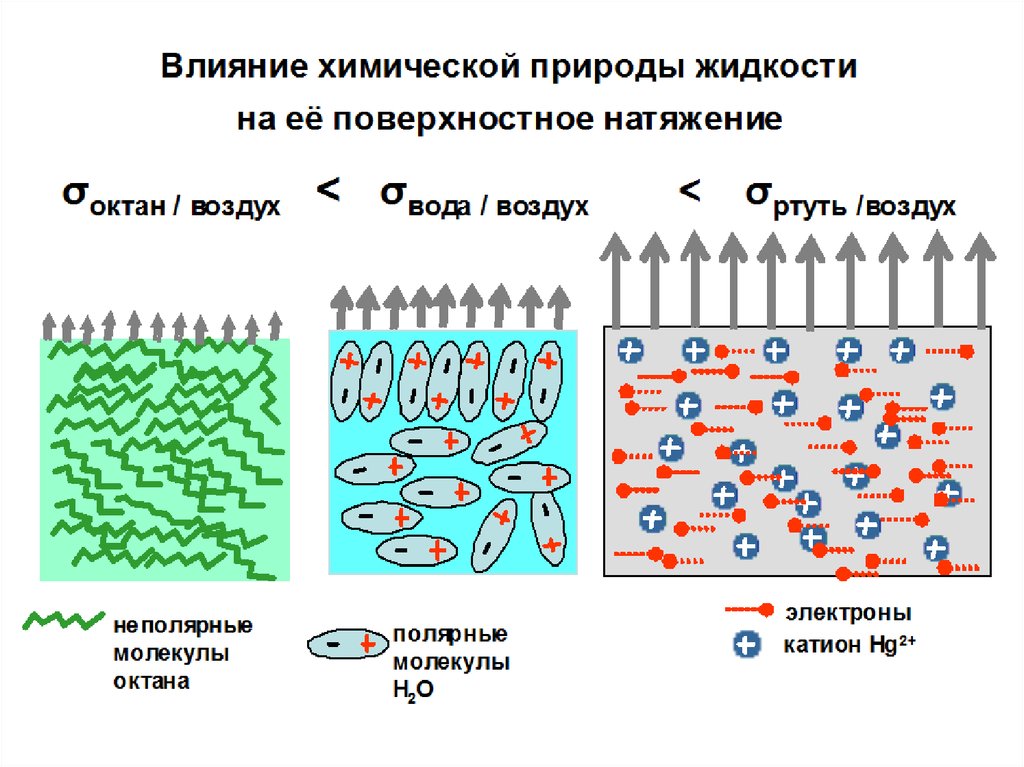
- удельная поверхностная энергия Gsуд
Поверхностное натяжение индивидуальных веществ на границе с воздухом
Вещество
σ, мДж/м2
Вещество
σ, мДж/м2
Гелий (–270 оС)
0,22
Ртуть (25 оС)
473,5
Азот (–193 оС)
8,27
NaCl (801 оС)
113,8
Гексан (20 ºС)
18,41
Свинец (350 оС)
442,0
Бензол
(25 оС)
Вода (25 оС)
28,2
71,9
Платина (2000
оС)
Алмаз (25 оС)
1819,0
11400,0

8.

9.

Характеристика межфазной поверхности
Поверхностный слой (ПС) – это переходная область, в которой свойства объемных фаз
переходят друг в друга по неизвестному закону. (кривая 1)
Толщина поверхностного слоя h - это расстояние по обе стороны от границы раздела фаз, за
пределами которого свойства поверхностного слоя перестают отличаться от свойств
объемных фаз.
Оценка свойств поверхностного слоя
1) Метод слоя конечной толщины (Гугенгейм)
Поверхностный слой имеет некоторый объем. Границы
объёмных фаз совпадают с границами поверхностного
слоя.(кривая 1)
2) Метод избыточных величин (Гиббс )
Фазы и считаются однородными вплоть до РП. Эта разделяющая
поверхность обладает избыточными термодинамическими
параметрами по сравнению с параметрами объемных фаз, но не имеет
объема. (кривая 2) (РП «нулевой толщины»)
Рис. 1 Иллюстрация метода слоя конечной
толщины и метода избытков Гиббса
n.c.

10. Энергетические параметры поверхности

Для избытка энтальпии (все относим к ед. площади поверхности) :
H S G S T S S
(1)
Где H S , G S , S S – соответственно избытки энтальпии, энергии Гиббса и энтропии для поверхностного слоя.
Для избытка внутренней энергии
U S будем иметь то же выражение, так как
U S G S T S S
(2)
Для избытка энтропии в соответствии со II началом термодинамики запишем:
S S q S / T
Где
qS –
(3)
избыток теплоты.
S
S
S
U
G
q
Тогда, подставляя (3) в (2), получим
q S > 0, то U s G s,
(4)
ее обычно называют полной поверхностной энергией
, Vп.с.
= 0:

11.

Из объединенного уравнения I и II начал термодинамики для поверхностного слоя при постоянстве всех
параметров, кроме температуры, следует:
dG S dT
S
S
(5)
Для конечного изменения
G S
S
T S
P
(6)
G S
S
T S
P
(7)
G S
S
S
U
G
T
Подставив (7) в (2), определим
T
P
Учитывая, что G для I единицы поверхности равно
S
(8)
, получим
U S T
T P
Уравнения (8) и (9) являются уравнениями Гиббса-Гельмгольца для поверхностного слоя.
С учетом уравнений (7) и (3) имеем:
G S
qS
T T T
P
P
(10)
(9)

12. Для большинства жидкостей эта зависимость линейна и имеет вид:

0 aT ;
(11)
a,
T
(12)
где а – это снижение σ при повышении температуры на один градус
(температурный коэффициент поверхностного натяжения).
Например, для воды а = 0,154, тогда полная поверхностная энергия
для воды:
ΔUs = σ – T(дσ/дT) = 72,5 – 298(–0,154) = 118,5 мДж/м2
при t = 25 0C. Расчеты показывают, что для многих веществ ΔUs состоит
примерно наполовину из σ и qs

13.

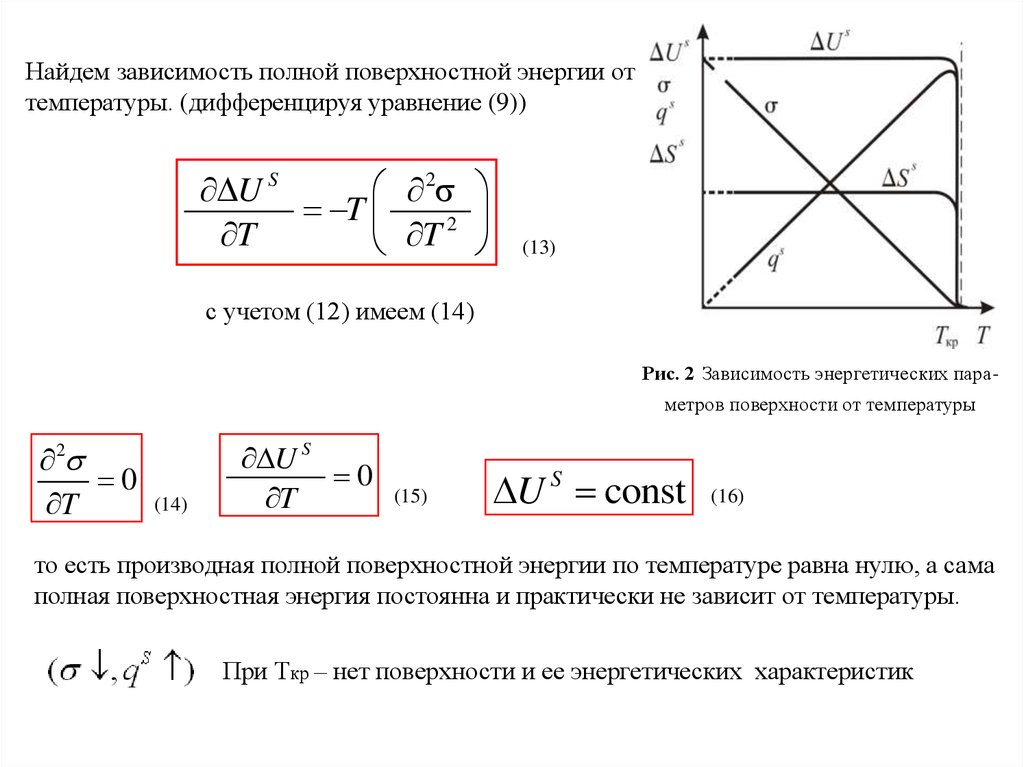
Найдем зависимость полной поверхностной энергии от
температуры. (дифференцируя уравнение (9))
2
U S
T
2
T
T
(13)
с учетом (12) имеем (14)
Рис. 2 Зависимость энергетических параметров поверхности от температуры
2
0
T
(14)
U S
0
T
(15)
U S const
(16)
то есть производная полной поверхностной энергии по температуре равна нулю, а сама
полная поверхностная энергия постоянна и практически не зависит от температуры.
При Ткр – нет поверхности и ее энергетических характеристик