Похожие презентации:
Размерная цепь
1. Ссылки на ГОСТы
• Ряды нормальных линейных размеров поГОСТ 6636-86 на основе рядов предпочт.
чисел.
• Основные нормы взаимозаменяемости.
Характеристики изделий геометрические.
Система допусков на линейные размеры.
ГОСТ 25346-2013
• Нанесение размеров и предельных
отклонений по ГОСТ 2.307-2011
2. Пример выбора посадки расчетным путем
Назначить посадку в системе отверстия ø25из условия:
-10 ≤ D - d ≤ +30 мкм
ES
Диапазон посадки:
TS = TD + Td
es-?
0
0
ei-?
3. Пример выбора посадки расчетным путем
ES – ei ≤ 30 мкм ;EI – es ≥ -10 мкм .
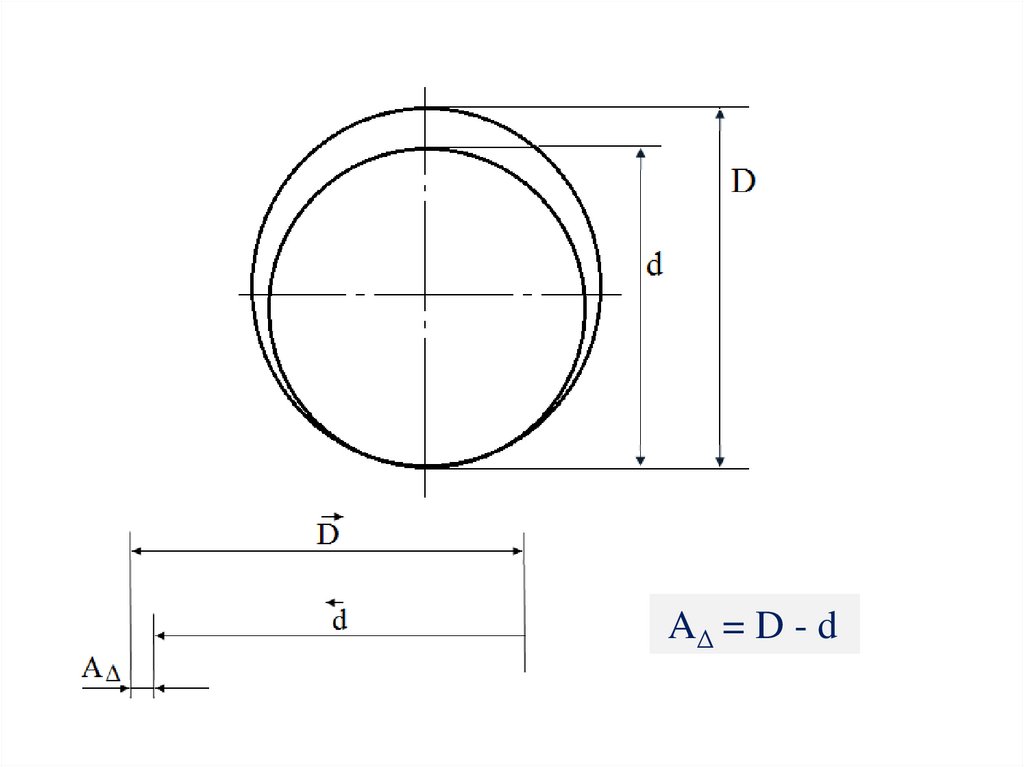
4.
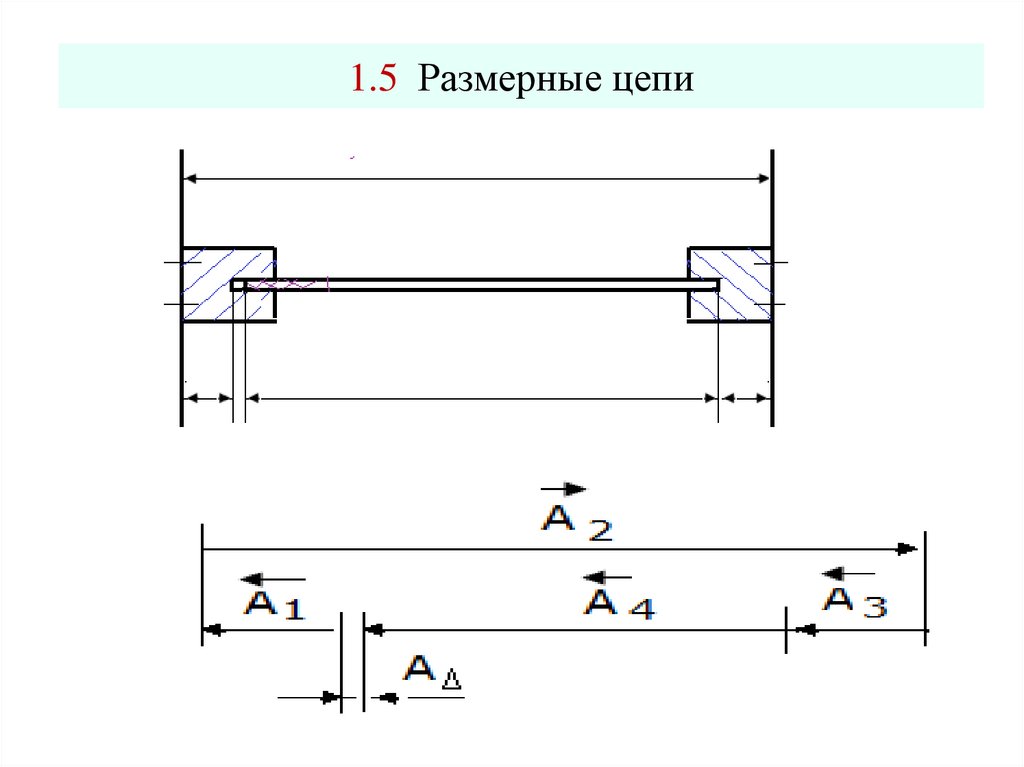
AΔ = D - d5. 1.5 Размерные цепи
6. Размерная цепь в задаче измерения
7. Угловая РЦ
Обеспечениедопустимого
отклонения от
параллельности
плоскостей
8. Что такое размерная цепь (РЦ)
• РЦ – совокупность размеров, относящихся кизделию, взаимосвязанных при решении
определенной задачи (конструкторской,
технологической, измерительной) и
образующих замкнутый контур (цепь),
где каждый размер – звено цепи.
В РЦ всегда есть одно – замыкающее звено, которое получается последним при
решении задачи. При постановке задачи
такое звено называют исходным.
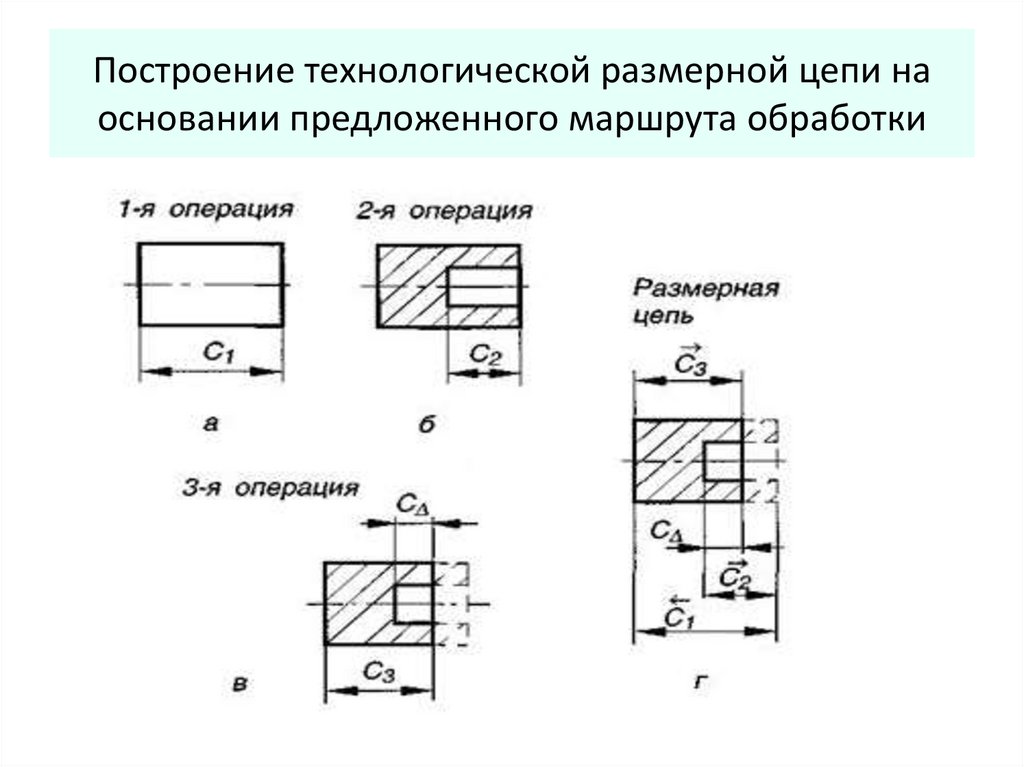
9. Построение технологической размерной цепи на основании предложенного маршрута обработки
10. Составляющие звенья РЦ
Итак, в РЦ всегда есть замыкающее (исходное)звено. Остальные звенья (размеры) РЦ –
составляющие. Все они по отношению к
замыкающему (исходному) звену делятся на
увеличивающие и уменьшающие размеры
(звенья), в зависимости от того, увеличивается или
уменьшается
замыкающий
размер
при
увеличении рассматриваемого составляющего
звена.
11.
Основные идеи теорииразмерных цепей мы изучаем на
примерах схем плоских РЦ с
параллельными звеньями
РЦ составляются для решения
задач проектного расчета (синтеза)
и проверочного расчета (анализа).
12. Задача ПРОЕКТНОГО расчета (задача синтеза) РАЗМЕРНЫХ ЦЕПЕЙ
Заданинтервал (А∆э.нм, А∆э, нб)
эксплуатационных допустимых значений
замыкающего звена и номинальные
значения всех размеров цепи.
Определить интервалы допустимых
значений размеров составляющих
звеньев (Аjнм, Аjнб)-?
13. Расчет размерных цепей из условий полной и неполной взаимозаменяемости
Метод полной взаимозаменяемости (В)(метод расчета на максимум—минимум)
учитывает самые неблагоприятные
сочетания предельных отклонений
звеньев размерной цепи.
Вероятностный метод расчета учитывает
рассеяние размеров и вероятность
различных сочетаний отклонений
составляющих звеньев размерной цепи,
соответствуя неполной В.
14. Расчетные соотношения для решения задач РЦ методом максимума-минимума
mA Aj ув
j 1
p 1
A ум;
j m 1
j
m
p 1
p 1
j 1
j m 1
j 1
T T j ув T j ум T j
m
p 1
1
m 1
E S ( A ) E S ( A j ) ув Ei ( A j ) ум
m
p 1
1
m 1
Ei ( A ) Ei ( A j ) ув E S ( A j ) ум
15. Расчетные соотношения для решения задач РЦ методом максимума-минимума
mp 1
j 1
j m 1
m
p 1
j 1
j m 1
A max А j max A j min
A min А j min A j max
m
p 1
p 1
T T À j T A j T j
j 1
j m 1
j 1
16. Допуск замыкающего размера равен сумме допусков составляющих звеньев, след.:
• если к какому-либо размеру предъявляютсявысокие требования по точности, то нужно
составить такую последовательность
обработки, чтобы этот размер не был
замыкающим, а был составляющим.
• при конструировании надо соблюдать
правило кратчайшей размерной цепи, т.е.
число звеньев в размерной цепи должно
быть минимальным.
17. Решение задачи проектного расчета (синтеза) РЦ из условия полной взаимозамен. способом равноточных допусков
Здесь стремятся получить допуски составляющихразмеров по одинаковым квалитетам.
ITj = nср· ij (A) ,
где ij (A) – единица допуска размера А.
p 1
p 1
T IT j
nср Т / i j ;
1
1
Nкв
5
6
7
8
9
10
…
16
17
18
n
7
10
16
25
40
64
…
1000
1600
2500
18. Условия, проверяемые при решении задачи РЦ методом максимума—минимума
p 1T IT j
1
TΔ – ΣITj ≤ 0.05 TΔ ,
То есть допуск ТΔ не должен
отличаться от суммы допусков ITj
больше, чем на 5%
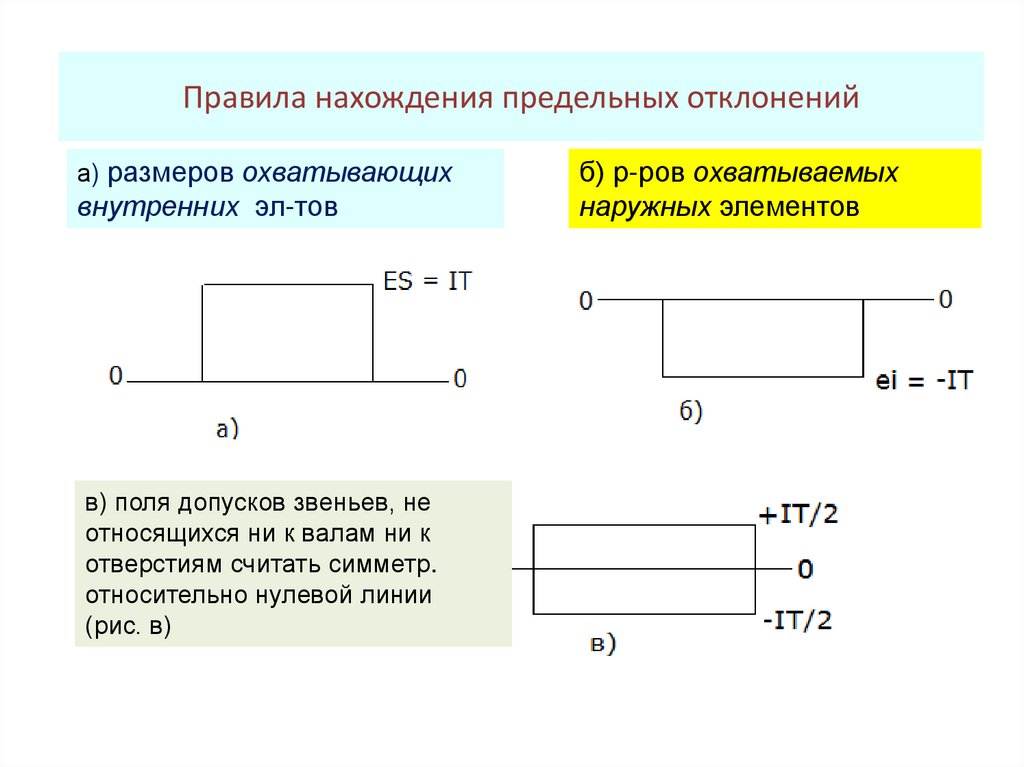
19. Правила нахождения предельных отклонений
а) размеров охватывающихвнутренних эл-тов
в) поля допусков звеньев, не
относящихся ни к валам ни к
отверстиям считать симметр.
относительно нулевой линии
(рис. в)
б) р-ров охватываемых
наружных элементов
20. Увязочное (резервное ) звено
mp 1
1
m 1
E S ( A ) E S ( A j ) ув Ei ( A j ) ум;
m
p 1
1
m 1
Ei ( A ) Ei ( A j ) ув E S ( A j ) ум
Например,
ESΔ = ES2 – Ei1 - Ei3 - Ei4 ;
EiΔ = Ei2 – ES1 – ES3 – ES4 .
21. Увязочное (резервное ) звено
mp 1
1
m 1
E S ( A ) E S ( A j ) Ei ( A j );
m
p 1
1
m 1
Ei ( A ) Ei ( A j ) E S ( A j ).
Например,
ESΔ = ES2 – Ei1 - Ei3 - Ei4 ;
EiΔ = Ei2 – ES1 – ES3 – ES4 .
22. Пример расчета РЦ
А1 =А3 = 18 мм; А2 = 100 мм; А4 = 64 мм20 ≤ АΔ ≤ 110 мкм
Ei(Aj) - ?, Es(Aj) - ?
23. Пример расчета РЦ (см. выше)
А1 =А3 = 18 мм; А2 = 100 мм; А4 = 64 ммj
1
2
3
4
I, мкм
1,1
2,2
1,1
1,9
90
nср
14,3
2 1,1 2,2 1,9
Nкв
5
6
7
8
9
n
7
10
16
25
40
24. Пример расчета РЦ (продолж)
Интервалы размеров, ммСвыше
»
»
»
»
»
»
3
6
10
18
30
50
80
до
»
»
»
»
»
»
6
10
18
30
50
80
120
КВАЛИТЕТЫ
5
6
7
8
9
10
5
8
12
18
30
48
6
9
15
22
36
58
8
11
18
27
43
70
9
13
21
33
52
84
11
16
25
39
62
100
13
19
30
46
74
120
15
22
35
54
87
140
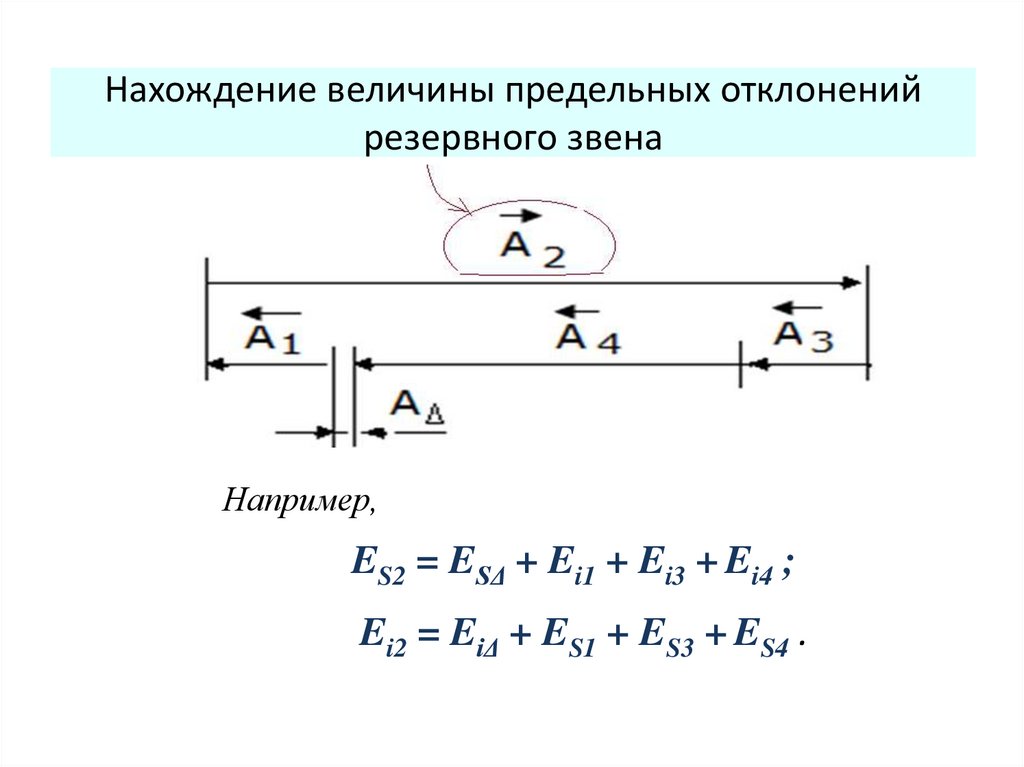
25. Нахождение величины предельных отклонений резервного звена
Например,ES2 = ESΔ + Ei1 + Ei3 + Ei4 ;
Ei2 = EiΔ + ES1 + ES3 + ES4 .
26. Нахождение величины предельных отклонений резервного звена: числ. пример
Например,ES2 = 110 – 9 - 9 – 19 = 73 МКМ ;
Ei2 = 73 – 35 = 38 МКМ.
27.
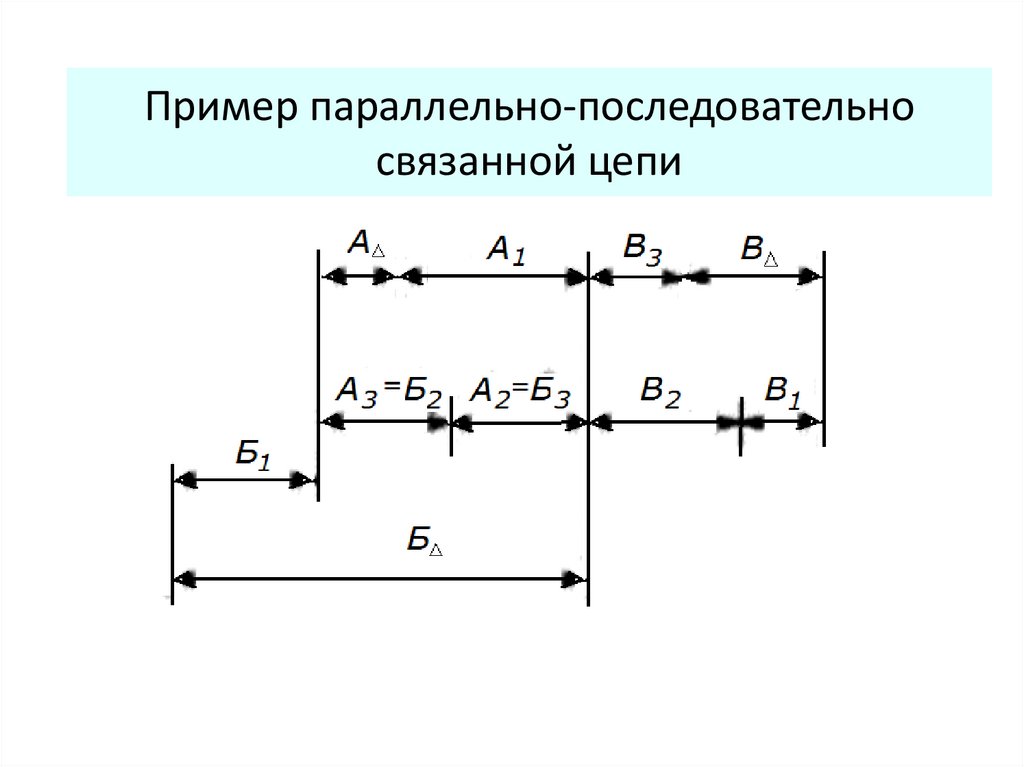
28. Пример параллельно-последовательно связанной цепи
29. Размерные цепи с неколлинеарными звеньями
(два вектора называются коллинеарными,если прямые, проходящие в их направлениях
параллельны)
Если звенья РЦ не ориентированы
параллельно, то вектор составляющего
звена Аj берется как проекция на линию
замыкающего звена АΔ .
30. Пример плоской размерной цепи с непараллельными звеньями
Расположенное под углом звено включается в РЦсвоей проекцией на направление замыкающего
звена (то есть переходим к коллинеарной РЦ со
звеном А3 · cos α).
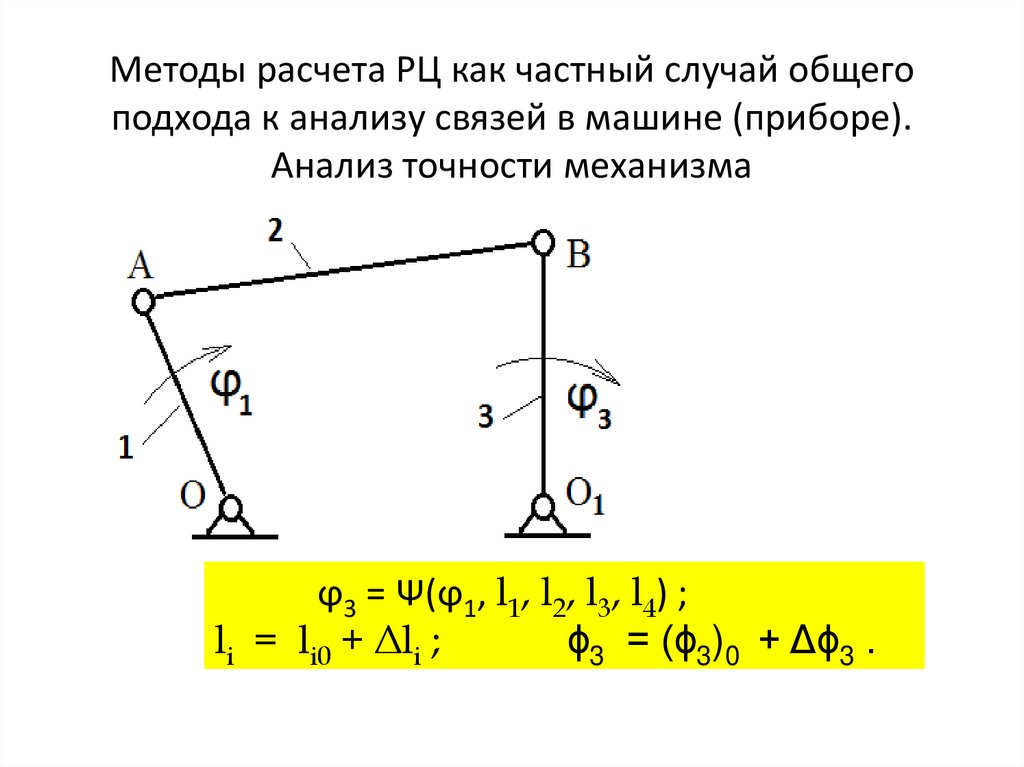
31. Методы расчета РЦ как частный случай общего подхода к анализу связей в машине (приборе). Анализ точности механизма
ϕ3 = Ψ(ϕ1, l1, l2, l3, l4) ;li = li0 + Δli ;
ϕ3 = (ϕ3)0 + Δϕ3 .
32. 1.6. Вероятностный расчет размерных цепей и сопряжений
При расчете по максимуму-минимуму неисключаются самые маловероятные сочетания
предельных размеров, что приводит к
неоправданному ужесточению допусков
Все размеры в основной формуле расчета РЦ
A j A j
являются величинами случайными
След., к расчету РЦ можно применить
положения теории вероятн. в отношении
суммирования случайных величин
33. Информация для вероятностного расчета – закон распределения
Закон распределения – всякое соотношение,устанавливающее связь между возможными
значениями случайной величины (СВ) и
соответствующими им вероятностями.
Закон распред. показывает, как суммарная
вероятность распределена между
отдельными значениями СВ.
n
p 1
i 1
i
34.
Пример распределения дискретной СВx
p(xi)
1
1/20
2
3/20
3
8/20
4
5/20
5
3/20
5
p 1
i 1
i
35. Интегральный закон распределения дискретной случайной величины
36. Закон распределения. Плотность вероятности
P (X < x) = F (x)P (X < x + dx) = P (X < x) + P (x < X < x + dx).
F ( x dx ) F ( x ) dF ( x )
f ( x)
lim
dx
dx
dx 0
37. Размеры - случайные величины
Пример: в партии валов из 100 штукдиаметр принимает значения от dmin=32,13
мм до dmax=32,36 мм (то есть ω = 0,23 мм).
Таблица распределения значений d вала:
1)
2)
3)
4)
5)
6)
32,13 – 32,16
32,17 – 32,20
32,21 – 32,24
32,25 – 32,28
32,29 – 32,32
32,33 – 32,36
3
11
36
40
6
4
0,03
0,11
0,36
0,40
0,06
0,04
38.
Гистограмма (1) и практическая криваяраспределения (2 ) случайной величины d
39.
Математическое ожидание – суммапроизведений всех возможных значений
случайной величины на вероятности
этих значений:
n
mx xi pi
1
mx x f ( x ) dx
40. Дисперсия СВ
Dx ( x mx ) f ( x )dx2
[X ]
D[ X ]
41. Положения теории вероятностей в отношении суммирования случайных величин
M [ X i ] M [ X i ]D[ X i ] D[ X i ] 2 K i j
i j
Для слабо коррелированных
случайных величин
Ki j 0
42. Поле рассеивания при нормальном з-не и поле допуска
На основании трактовки размера как нормальнораспределенной случайной величины с T / 6
для коллинеарной РЦ
T
p 1
(T )
j 1
j
2
43. Решение проектной задачи РЦ вероятностным методом способом равноточных допусков
;Решение проектной задачи РЦ
вероятностным методом
способом равноточных допусков
nср
T
i
2
j
Значения n ср округляются до стандартных, после
чего выбираются №№ приемлемых квалитетов и
проверяется условие
IT
2
j
T
44. Верхнее Es , нижнее Ei и среднее Em отклонения
;;
.
Верхнее Es , нижнее Ei
и среднее Em отклонения
Es ( A ) Em ( A ) T / 2
Ei ( A ) Em ( A ) T / 2
E s ( A j ) E m ( A j ) IT j / 2
Ei ( A j ) E m ( A j ) IT j / 2
45. Верхнее Es , нижнее Ei и среднее Em отклонения
mp 1
j 1
m 1
Em ( A ) Em ( Aj ) ув Em ( Aj ) ум
E s Ei
Em
2
46. Пример расчета РЦ
А1 =А3 = 18 мм; А2 = 100 мм; А4 = 64 мм20 ≤ АΔ ≤ 110 мкм
Ei(Aj) - ?, Es(Aj) - ?
47. Пример расчета РЦ (продолж.)
j1
I, мкм 1,1
nср
2
3
4
2,2
1,1
1,9
T
2
i
j
90
1,12 * 2 2,22 1,92
Nкв
5
6
7
8
9
10
n
7
10
16
25
40
64
27,3ед
48. Пример расчета РЦ (продолж.)
j1
2
3
4
ITj ,мкм
27
54
27 (43)
46
Интервалы размеров, 5
мм
6
7
8
9
10
11
Свыше
»
»
»
»
»
»
8
9
11
13
16
19
22
12
15
18
21
25
30
35
18
22
27
33
39
46
54
30
36
43
52
62
74
87
48
58
70
84
100
120
140
75
90
110
130
160
190
220
3
6
10
18
30
50
80
до
»
»
»
»
»
»
6
10
18
30
50
80
120
5
6
8
9
11
13
15
49. Сопоставл. с расчетом по методу макс.-мин.
nср = 14,3 ед,то есть IT1 = IT3 = 18 мкм (7-й кв)
IT2 = 35 мкм; IT4 = 19 мкм (6-й кв.)
Nкв
6
7
8
9
10
n
10
16
25
40
64
18 + 18 + 35 + 19 = 90 мкм
(
27 2 432 54 2 46 2 87 мкм )
50.
Tn
p 1
t
2
i
i
2
1
t∆ - коэффициент, который зависит от принятой
вероятности риска выхода величины за пределы
допуска.
Pиск%
32
10
4.5
1.0
0.27
0.1
0.01
t∆
3.89
1
1.65
2
2.57
3
3.29
Коэффициент λ характеризует закон распределения
погрешностей звеньев;
λ2=1/9 для нормального закона (Гаусса)
51. 1.6-bis Вероятностный расчет сопряжений
Типовые задачи:- найти вероятность получения в переходном
сопряжении зазора (натяга);
- найти величину наибольшего (наименьшего)
зазора или натяга в сопряжении.
Случайная величина (СВ) в том и другом
случаях - величина зазора (натяга) в
сопряжении. Эта СВ является суммой
размеров отверстия и вала, считающихся
нормально распределенными СВ.
52. 1.7. Обеспечение точности РЦ при неполной взаимозаменяемости
• 1) методом групповой В-сти (селективнаясборка);
• 2) методом пригонки и совместной
обработки (технологическим);
• 3) – ,, - регулирования (конструкторским).
При вероятностном методе расчета
точность замыкающего звена достигается не
для всех соотв. чертежу реализаций размеров.
53. Метод регулирования
К – сменныйкомпенсатор.
54. Регулирование дает возможность увеличить допуски Тj составляющих звеньев при заданном допуске замыкающего звена:
AΔнб = А2нб + Кнм – (А1 + А3 + А4)нм;AΔнм = А2нм + Кнб – (А1 + А3 + А4)нб .
Отсюда
ТΔ + ТК = ΣТj .
































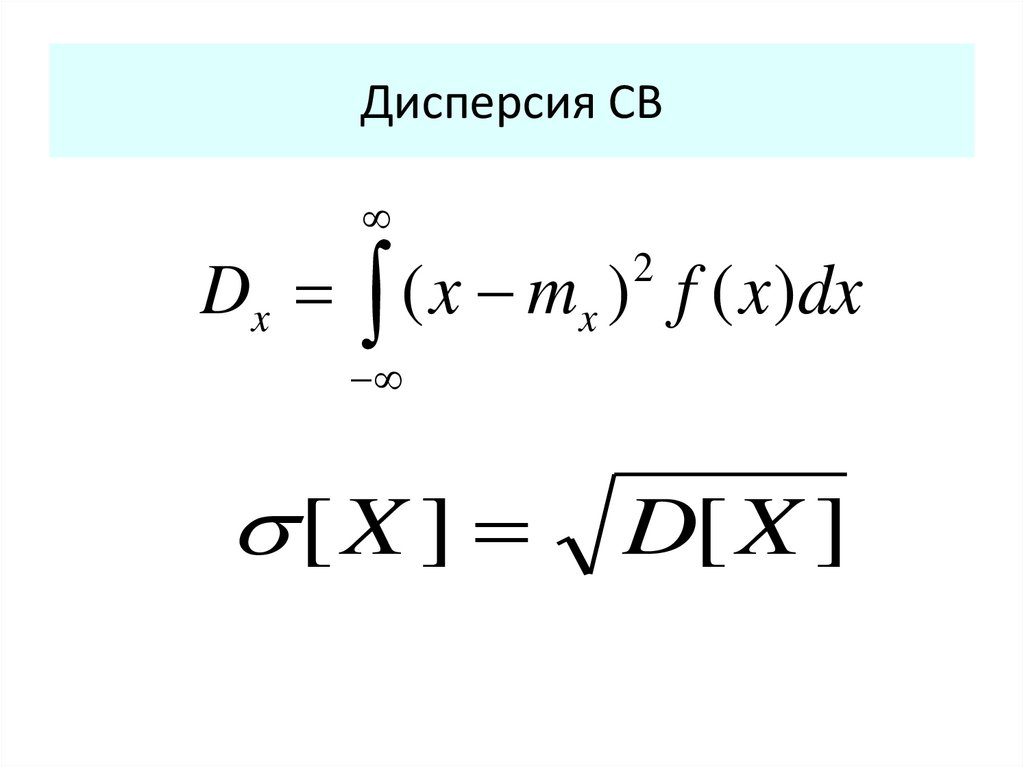















 Механика
Механика








