Технологические размерные расчеты. (Тема 8)

1. Тема 8. Технологические размерные расчеты

1

2. Размерные технологические цепи и их характеристики

Размерной
цепью
называется
совокупность
размеров,
расположенных по замкнутому контуру. Все размеры деталей,
составляющие размерную цепь, называют звеньями. Звенья цепи,
кроме замыкающего, называют составляющими.
На рисунке, для нормальной работы ролика необходимо обеспечить
зазор ∆. На величину этого зазора влияют размеры А1 и А2 . Для
рассматриваемого случая уравнение размерной цепи имеет вид
А1 – А2 - ∆ = 0.
∆- замыкающее звено. По расположению звеньев размерные цепи
делятся на линейные, плоские и пространственные.
Составляющие
звенья
делятся
на
увеличивающие
и
уменьшающие.
Увеличивающее звено такое, если с его
увеличением
замыкающее
звено
увеличивается. Уменьшающее звено при
своем увеличении вызывает уменьшение
замыкающего звена.
2

3. Размерные технологические цепи и их характеристики

Линейная размерная цепь имеет все размеры, параллельные
между собой и связанные линейной зависимостью.
Плоская размерная цепь содержит звенья, находящиеся в
одной или нескольких параллельных плоскостях, которые
могут быть спроектированы без изменения их величины на
одну плоскость.
Пространственная размерная цепь состоит из звеньев
которые не параллельные и лежат в непараллельных
плоскостях. Звенья могут быть спроектированы на три
координатные плоскости. Пространственная размерная цепь
может быть приведена к трем плоским размерным цепям. Если
в плоской размерной цепи имеются звенья, расположенные под
углом к выбранному направлению, то они проектируются на
выбранное направление.
3

4. Задачи, решаемые при расчете размерных цепей

Прямая задача (проектный расчет).
По заданным параметрам замыкающего звена определяются параметры
составляющих звеньев. При этом по известным предельным отклонениям и
допуску замыкающего звена, называемому в этом случае исходным,
рассчитывают допуски и предельные отклонения размеров составляющих
звеньев.
Обратная задача (проверочный расчет).
По известным параметрам составляющих звеньев определяются параметры
замыкающего звена. При этом по известным номинальным размерам и их
предельным отклонениям, допускам и характеристикам рассеяния размеров
составляющих звеньев рассчитываются номинальный размер замыкающего
звена, его допуск, или поле рассеивания и предельные отклонения.
Технологические размерные цепи рассчитываются следующими способами:
на максимум-минимум (метод полной взаимозаменяемости);
вероятностным методом (метод неполной взаимозаменяемости);
методом групповой взаимозаменяемости (при селективной сборке);
с учетом регулирования размеров при сборке;
с учетом пригонки размеров отдельных деталей при сборке.
Выбор способа расчета зависит от принятого в его основу метода достижения
требуемой точности изделия.
4

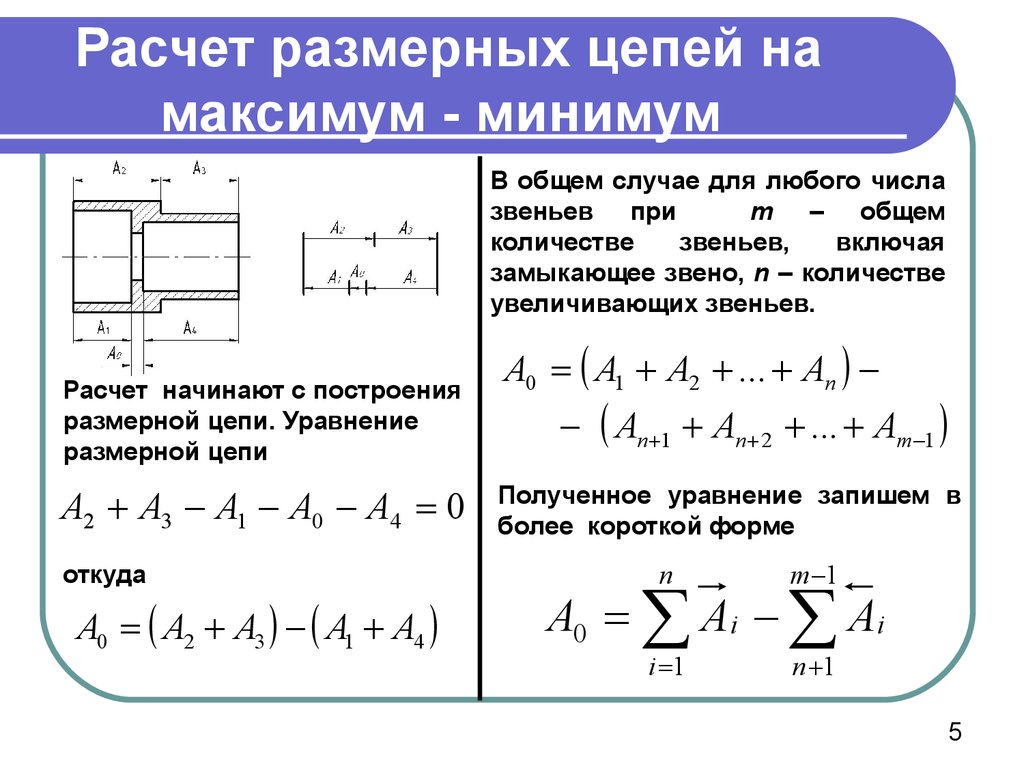
5. Расчет размерных цепей на максимум - минимум

В общем случае для любого числа
звеньев при
m – общем
количестве
звеньев,
включая
замыкающее звено, n – количестве
увеличивающих звеньев.
Расчет начинают с построения
размерной цепи. Уравнение
размерной цепи
А2 А3 А1 А0 А4 0
откуда
А0 А2 А3 А1 А4
А0 А1 А2 ... Аn
An 1 An 2 ... Am 1
Полученное уравнение запишем в
более короткой форме
n
m 1
i 1
n 1
А0 A i Ai
5

6. Расчет размерных цепей на максимум - минимум

Наибольший свой размер замыкающее звено получит тогда, когда
увеличивающие звенья
будут наибольшим, а уменьшающие –
наименьшими, т.е.
А
А
А
А0max А1max А2max ... Аnmax
min
n 1
А
... А
min
n 2
min
m 1
По аналогии, наименьший размер замыкающего звена
min
0
А
min
1
А
min
2
А
max
n 1
Определим допуск замыкающего звена
TA 0 TA1 TA 2 ... TA m 1 ,
... А
max
n 2
min
n
... А
max
m 1
m 1
TА0 TAi
i 1
6

7. Расчет размерных цепей на максимум - минимум

Верхнее предельное отклонение замыкающего звена
получим вычитанием из его наибольшего предельного
значения номинального, т.е.
n
m 1
ESA0 ES Ai EI Ai
i 1
n 1
Аналогично
нижнее
предельное
отклонение
замыкающего звена
получим вычитанием из его
наименьшего предельного значения номинального, т.е.
n
m 1
i 1
n 1
EIA0 EI Ai ES Ai
7

8. Расчет размерных цепей, обеспечивающий неполную взаимозаменяемость

Рассмотрим порядок расчета допуска замыкающего звена (обратную
задачу).
На практике
законы распределения часто неизвестны (при
проектных расчетах) поэтому применение вероятностного метода
m 1 4.
расчета считается правильным при
В соответствии с положениями теории вероятностей суммирование
случайных величин производится квадратично.
Допуск замыкающего звена равен
m 1
ТА0 t
TA
i 1
2
i
2
i
где t – коэффициент риска, характеризующий вероятность выхода
отклонений
замыкающего
звена
за
пределы
допуска
(нормированный параметр распределения).
При m 1 4 принимается t = 3
Относительное среднее квадратическое отклонение определяется
по формуле
1
i
t
8

9. Расчет размерных цепей, обеспечивающий неполную взаимозаменяемость

При распределении размеров составляющих звеньев по закону
нормального распределения для линейной размерной цепи
с
числом звеньев, больше 4
ТА 0
m 1
TA
i 1
2
i
При проектных расчетах, когда законы распределения неизвестны,
условно принимается распределение всех звеньев одинаковым,
соответствующим закону Симпсона. Тогда
ТА0 1,2
m 1
2
TA
i
i 1
9

10. Расчет размерных цепей, обеспечивающий неполную взаимозаменяемость

Выполним расчет допусков составляющих звеньев (рассмотрим
прямую задачу).
Расчет начинается с определения величины среднего допуска составляющих
звеньев
Tcp TA 0 / 1,2 m 1
Если средняя точность размеров составляющих звеньев соответствует 1112 квалитетам, то метод неполной взаимозаменяемости считается
подходящим, и определенный расчетом квалитет принимается в основу для
установления
допусков размеров всех составляющих звеньев, кроме
регулирующего. Если по расчетам средняя точность размеров составляющих
звеньев 7-9 квалитета, то достижение требуемой точности замыкающего
звена методом неполной взаимозаменяемости затруднена, необходима
пригонка. При необходимости производят выбор и расчет допуска
регулирующего звена.
В качестве регулирующего звена выбирается звено с наибольшим
номинальным размером, выполнение и измерение которого не вызывает
технологических трудностей. Допуск регулирующего звена рассчитывают по
формуле
m 2
1
2
ТA p
TA 0 k12TA i2
kp
i 1
где kр и ki
коэффициенты относительного
рассеяния
размеров
регулирующего
и
составляющих звеньев
10

11. Задачи, решаемые при расчете размерных цепей

ПОВТОР
Прямая задача (проектный расчет).
По заданным параметрам замыкающего звена определяются
параметры составляющих звеньев. При этом по известным
предельным отклонениям и допуску замыкающего звена,
называемому в этом случае исходным, рассчитывают допуски
и предельные отклонения размеров составляющих звеньев.
Обратная задача (проверочный расчет).
По
известным
параметрам
составляющих
звеньев
определяются параметры замыкающего звена. При этом по
известным номинальным размерам и их предельным
отклонениям,
допускам
и
характеристикам
рассеяния
размеров
составляющих
звеньев
рассчитываются
номинальный размер замыкающего звена, его допуск, или
поле рассеивания и предельные отклонения.
11

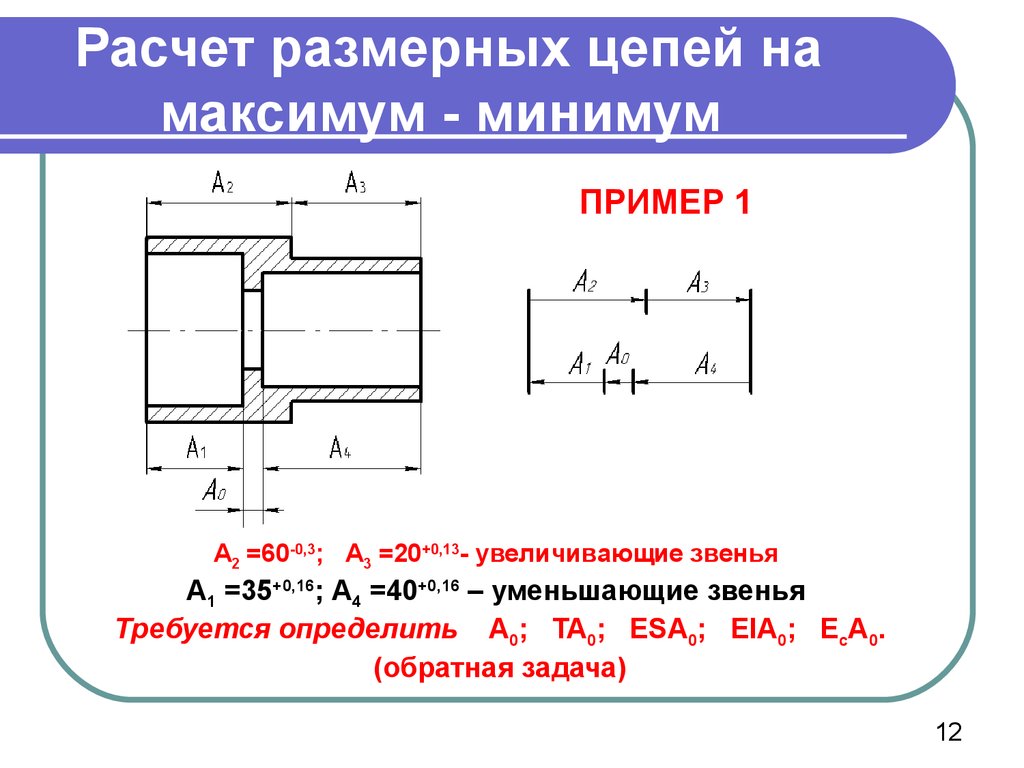
12. Расчет размерных цепей на максимум - минимум

ПРИМЕР 1
А2 =60-0,3; А3 =20+0,13- увеличивающие звенья
А1 =35+0,16; А4 =40+0,16 – уменьшающие звенья
Требуется определить А0; TA0; ESA0; EIA0; EcA0.
(обратная задача)
12

13. Расчет размерных цепей на максимум - минимум

A0=(A2+A3)- (A1+A4)=(60 + 20) – (35 + 40) = 5;
m 1
TА0 TAi
А2 =60-0,3; А3 =20+0,13; А1 =35+0,16; А4 =40+0,16.
TA0=0,3 + 0,13 + 0,16 + 0,16 = 0,75;
i 1
ES60=0; ES20=0,13; ES35=0,16; ES40=0,16;
EI60=-0,3; EI20=0; EI35=0; EI40=0;
n
m 1
i 1
n 1
ESA0 ES Ai EI Ai
ESA0=(0+0,13)-(0+0)=+0,13;
n
m 1
i 1
n 1
EIA0 EI Ai ES Ai
A0 5
EIA0=(-0,3+0)-(0,16+0,16)=-0,62;
TA 0
0,75
E c A0 ESA0
0,13
0,245 мм
2
2
0 ,13
0 , 62
13

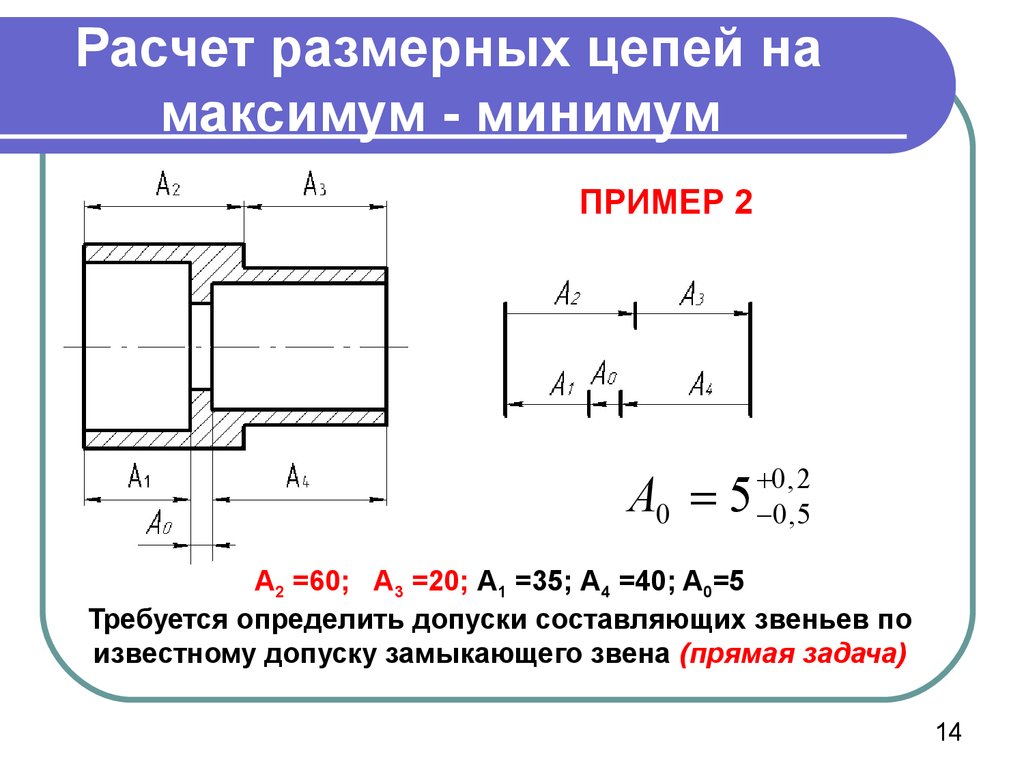
14. Расчет размерных цепей на максимум - минимум

ПРИМЕР 2
A0 5
0 , 2
0,5
А2 =60; А3 =20; А1 =35; А4 =40; A0=5
Требуется определить допуски составляющих звеньев по
известному допуску замыкающего звена (прямая задача)
14

15. Расчет размерных цепей на максимум - минимум

TA0 = 0,7
TAi ср = TA0 / (m-1) = 0,7/4 = 0,175 мм.
Для всех составляющих звеньев, кроме одного, самого
большого (регулирующего) назначаем допуски по Н или h,
соблюдая принцип «допуск в металл» и среднюю величину
допуска 0,175 мм. Регулирующим примем размер А2 =60.
В соответствии с таблицами допусков (Спр. Т.-М. Т.1, стр192)
А1 =35Н11 (+0,16); А4 =40Н11 (+0,16); А3 = 20Н11(+0,13).
TA1=0,16; TA4=0,16; TA3=0,13; EcA1=0,08; EcA4=0,08; EcA3=0,065;
EcA0=0,2-0,35=0,15.
Допуск регулирующего звена.
TA2 =0,7-(0,16+0,16+0,13)=0,25мм, что
m 2
соответствует 11 квалитету (0,19 мм).
ТА р ТА 0 TA i
Для 12 квалитета 0,3 мм.
i 1
Примем TA2=0,19.
15

16. Расчет размерных цепей на максимум - минимум

Координаты середины поля допуска регулирующего звена, когда
оно является увеличивающим:
n 1
m 2
i 1
n 1
E с A р E с A0 E с Ai E c Ai
A0 5 00,,25
А1 =35Н11 (+0,16); А4 =40Н11 (+0,16); А3 = 20Н11(+0,13); TA2=0,19.
EcA1=0,08; EcA4=0,08; EcA3=0,065; EcA0=0,2-0,35=-0,15.
Координаты середины поля допуска , если оно является
уменьшающим:
n
m 2
i 1
n 1
E с A p E с Ai E c Ai E c A0
Для А2=60: EcA2=-0,15-0,065+(0,08+0,08)=-0,055мм
ESA2= EcA2+TA2/2=-0,055+0,095=+0,04мм;
EIA2= EcA2-TA2/2=-0,055-0,095=-0,15мм.
Ap 60
0 , 04
0 ,15
16

17. Расчет размерных цепей на максимум - минимум

Окончательная
проверка установленных допусков
предельных отклонений производится по формулам
m 1
ТА0 TAi
i 1
n
m 1
i 1
n 1
и
E с A0 E с Ai E c Ai
А1 =35Н11 (+0,16); А4 =40Н11 (+0,16); А3 = 20Н11(+0,13); TA2=0,19.
EcA1=0,08; EcA4=0,08; EcA3=0,065; EcA0=0,2-0,35=-0,15.
EcA2=-0,055
TA0=0,16+0,16+0,13+0,19=0,64 мм.
EcA0=(+0,065-0,055)-(+0,08+0,08)=- 0,15 мм.
A0 5
0 , 2
0,5
17

18. Расчет размерных цепей методом неполной взаимозаменяемости

Точность замыкающего звена обеспечивается не у всех
деталей, а только у заранее обусловленной их части. При этом
предварительно устанавливается процент риска, т.е. процент
деталей, у которых может не обеспечиваться точность
замыкающего звена. Следует заметить, что процент риска - это
лишь вероятность получения бракованных изделий.
В основу метода расчета параметров составляющих
звеньев (прямая задача) положены следующие математические
зависимости.
Уравнение размерной цепи в номиналах и допуск замыкающего
звена
А
m
А
n
А
ТА t
m n
TA
2
i
2
i
ув
ум
1
t – коэффициент,
зависящий
от процента i риска;
λ
коэффициент, характеризующий закон рассеяния размеров.
i
–
18

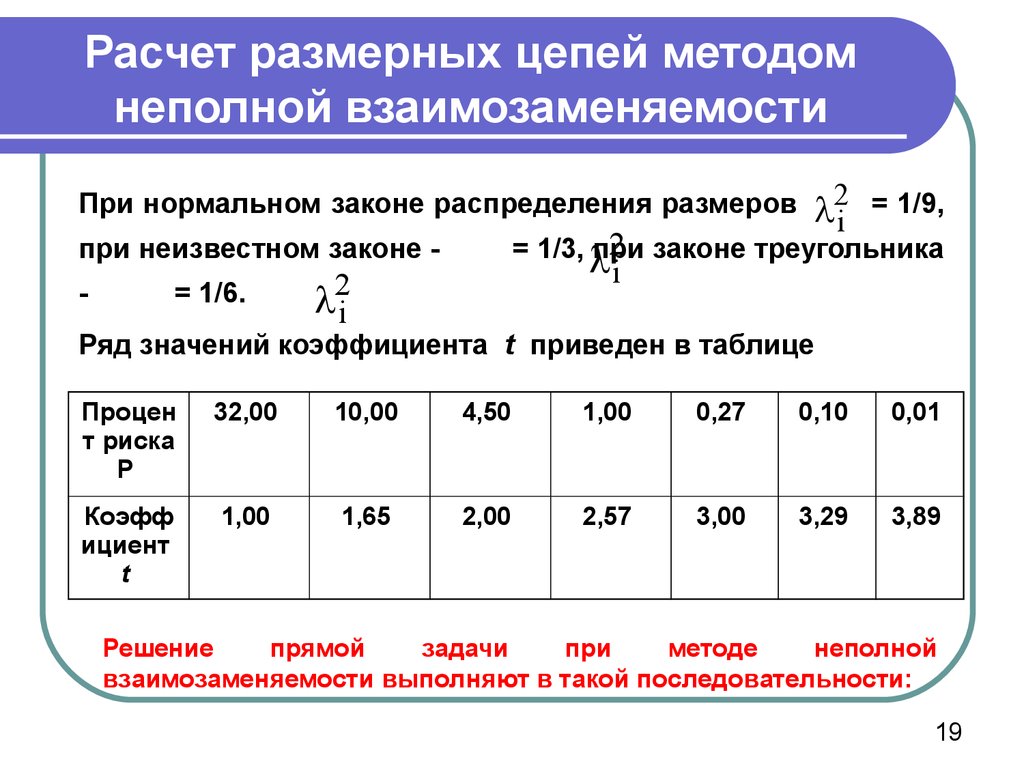
19. Расчет размерных цепей методом неполной взаимозаменяемости

При нормальном законе распределения размеров
= 1/6.
= 1/9,
2 законе треугольника
= 1/3, при
при неизвестном законе -
2i
i
2i
Ряд значений коэффициента t приведен в таблице
Процен
т риска
Р
32,00
10,00
4,50
1,00
0,27
0,10
0,01
Коэфф
ициент
t
1,00
1,65
2,00
2,57
3,00
3,29
3,89
Решение
прямой
задачи
при
методе
неполной
взаимозаменяемости выполняют в такой последовательности:
19

20. Расчет размерных цепей методом неполной взаимозаменяемости

1)записывают параметры исходного (замыкающего) звена:
номинальный размер АΔ, предельные отклонения ESAΔ и
EIAΔ, допуск ТΔ, координату середины поля допуска ЕСΔ;
2)по чертежу детали выявляют составляющие звенья Аi,
строят размерную цепь, определяют по ней увеличивающие
и уменьшающие звенья;
3)определяют номинальные размеры составляющих звеньев
Аi;
4)проверяют
правильность
определения
номинальных
значений составляющих звеньев по уравнению
m
n
А А ув А ум
20

21. Расчет размерных цепей методом неполной взаимозаменяемости

5)
задаются процентом риска
Р, определяют значение
коэффициента
t устанавливают законы распределения
составляющих звеньев и коэффициенты λi;
6) определяют среднее значение допусков составляющих
звеньев (существует способ назначения допусков одного
квалитета точности)
Т icp
T
m n
t
2
i
7) по номинальным размерам составляющих звеньев и с учетом
полученного среднего значения на все составляющие звенья,
кроме одного, назначают стандартные допуски по ГОСТ 2534782 (на одно звено может быть установлен нестандартный
допуск);
21

22. Расчет размерных цепей методом неполной взаимозаменяемости

8)
проверяют
правильность
определения
составляющих звеньев по формуле
ТА t
m n
допусков
TA
i 1
2
i
2
i
9) задают расположение допусков составляющих звеньев,
кроме одного звена (для охватывающих поверхностей
допуски задают ‘в плюс”, а для охватываемых – “в минус”,
для остальных симметрично);
10) определяют координаты середин полей допусков
составляющих звеньев, кроме одного звена, по формуле
ESAi EIAi
E ci
2
22

23. Расчет размерных цепей методом неполной взаимозаменяемости

11) определяют координату середины поля допуска, оставшегося
неизвестным звена из уравнения
m
n
E С Eс ув E с ум
12) определяют предельные отклонения оставшегося неизвестным
звена по формулам
ESAi = EcA i + 0,5TA i ,
EIAi = EcA i – 0,5TA i.
13) выполняют проверку правильности расчетов по формулам
m
n
ESA ECув ECу м t
m
n
EIA ECу в ECу м t
m n
(0,5TA ) ,
m n
2
i
2
i
(0,5TA )
2
i
i
2
.
23