Похожие презентации:
Застосування похідної до дослідження функцій та побудови графіків функцій
1.
Застосування похідної додослідження функцій та
побудови графіків функцій
2.
Дослідження властивостей функціїпроводитимемо за таким планом.
1. Знайти область визначення функції.
2. Дослідити функцію на парність.
3. Знайти нулі функції.
4. Знайти проміжки зростання і спадання
функції.
5. Знайти точки екстремуму та значення
функції в точках екстремуму.
6. Виявити інші особливості функції
(періодичність функції, поведінку функції в
околах окремих важливих точок тощо).
3.
1) y x 2 6 х 51) D(f) =R
2) f(x) ні парна ні непарна
3) – х2 + 6х – 5 = 0
D = 16
x1 =1
x2 = 5
4) у’= – 2x +6
+
– 2x +6 = 0
3
– 2x = – 6
x=3
f(x) зростає на ;3 f (x) спадає на 3;
хmax 3 точка екстремуму, точка максимуму
ymax =f(xmax) = – 32 + 6∙3 – 5 = 4
екстремум функції, максимум функції
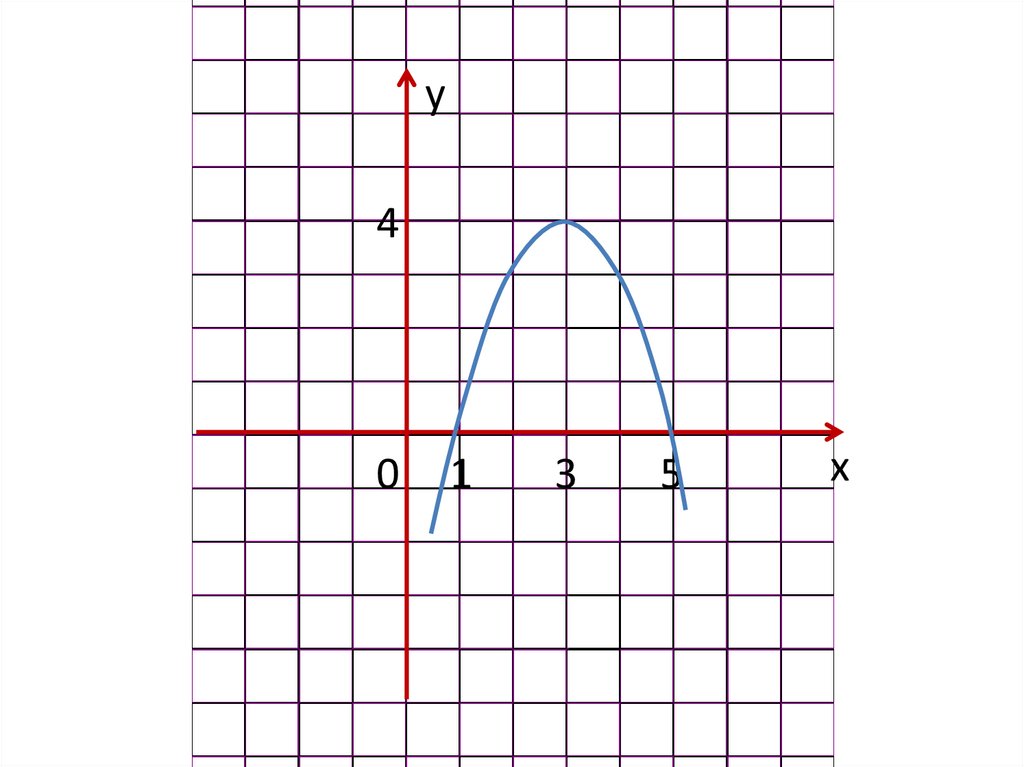
4.
y4
0
1
3
5
x
5.
2)1) D(f) =R
2) f(x) ні парна ні непарна
3) 3x2 – x3 = 0
x2 (3– x) = 0
x1 =0
x2 = 3
4) f ’(x) = 6x – 3x2
+
2
6x – 3x = 0
2
0
3x(2 – x) = 0
xmin = 0, xmax =2
f (0) = 3(0)2 – (0)3 = 0
f (-1) = 3(-1)2 – (-1)3 = 4
f (2) = 3(2)2 – (2)3 = 4
6.
y4
-1
0
2 3
x -1 0 2 3
y 4 0 4 0
x
7.
3) f (x) = (x2 – 2)21) D(f) =R
2) f (-x) = f (x) функція парна
3) (x2 – 2)2 =0
(( х 2)( х 2)) 2 0
х1 2, х2 2
4) f (x) = x4 – 4x2 + 4
f ’(x) = 4x3 – 8x
4x3 – 8x = 0
4x(x2 –2) = 0
xmin 2, xmax 0, xmin 2
f ( 2) = 0, f ( 2) =0,
f (-2) = 4, f (2) =4
-
+
2
f(0)=4
0 2
+
8.
y4
-2
20
2
2
3
x -2 2 0 2 2
y 4 0 4 0 4
x
9.
1) № 17.2 (3), стор. 172 (Нелін)2) f (x) = x3 + 3x2








 Математика
Математика








