Структурные модели пористых сред

1.

Структурные модели
пористых сред

2.

Реальные коллекторы углеводородного сырья имеют сложное строение пустотного
пространства, в связи с этим в подземной гидромеханике часто пользуются упрощенными
идеализированными моделями пористой среды. К таким моделям относятся идеальные
(капиллярные) и фиктивные (корпускулярные) грунты (среды). В корпускулярных моделях
пористая среда моделируются шарами, а в капиллярных моделях - капиллярными трубками.

3.

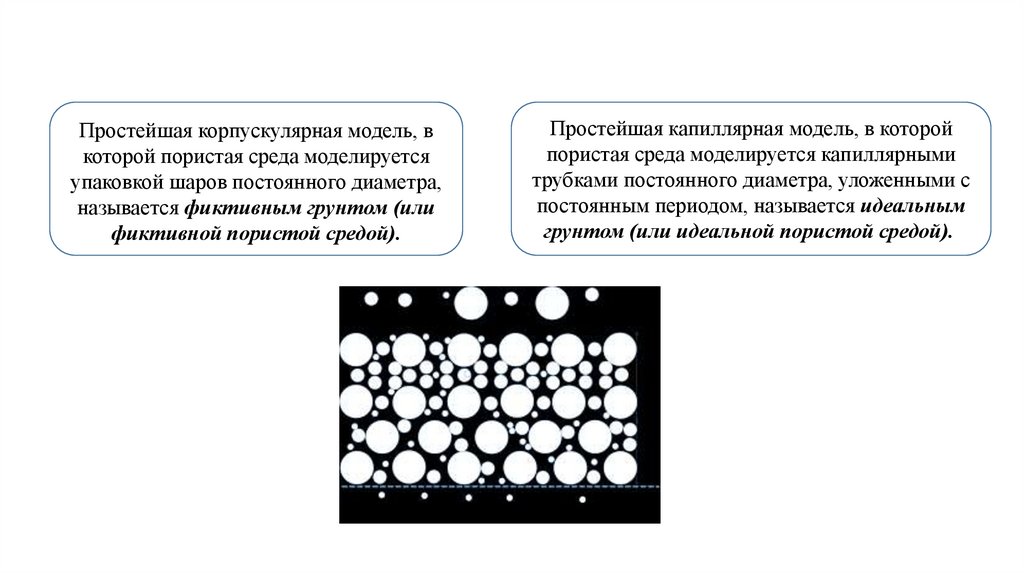
Простейшая корпускулярная модель, в
которой пористая среда моделируется
упаковкой шаров постоянного диаметра,
называется фиктивным грунтом (или
фиктивной пористой средой).
Простейшая капиллярная модель, в которой
пористая среда моделируется капиллярными
трубками постоянного диаметра, уложенными с
постоянным периодом, называется идеальным
грунтом (или идеальной пористой средой).

4.

Наиболее популярные модели фиктивного грунта получаются при наиболее плотных упаковках
шаров. Две основные упаковки — кубическая и гексагональная получаются следующим образом:
первый плоский слой уложен так, что каждый шар касается шести соседних, каждый шар второго
слоя помещается в углубление между тремя шарами первого слоя (рис. 1.8, 1.9).

5.

При наложении третьего слоя возможны два варианта. В первом варианте (кубическая упаковка)
каждый шар третьего слоя лежит на трех шарах второго слоя таким образом, что под шаром
третьего слоя нет шара первого слоя (рис. 1.10). Во втором варианте (гексагональная упаковка)
каждый шар третьего слоя лежит на трех шарах второго, но под каждым шаром третьего слоя
оказывается шар первого слоя.
Кроме указанной, наиболее плотной упаковки с
кубической симметрией рассматривают и такую
упаковку, когда в первом слое каждый шар
касается только четырех шаров, а все
последующие слои повторяют первый. Назовем
последнюю кубическую упаковку шаров рыхлой
кубической упаковкой. Для капиллярных
моделей идеального грунта наиболее простые
модели
получаются
при
взаимно
перпендикулярном расположении капилляров.

6.

Для фиктивного грунта достаточно просто
получается соотношение, которое связывает
удельную поверхность с пористостью упаковки т и
диаметром шаров D. Возьмем объем, в котором
имеется п шаров. Тогда весь объем можно
представить как сумму объема пустот и шаров -
Удельная поверхность, очевидно, равна
площади поверхности одного шара,
умноженной на число шаров в упаковке:
Из выписанных соотношений следует
Из полученного равенства получаем

7.

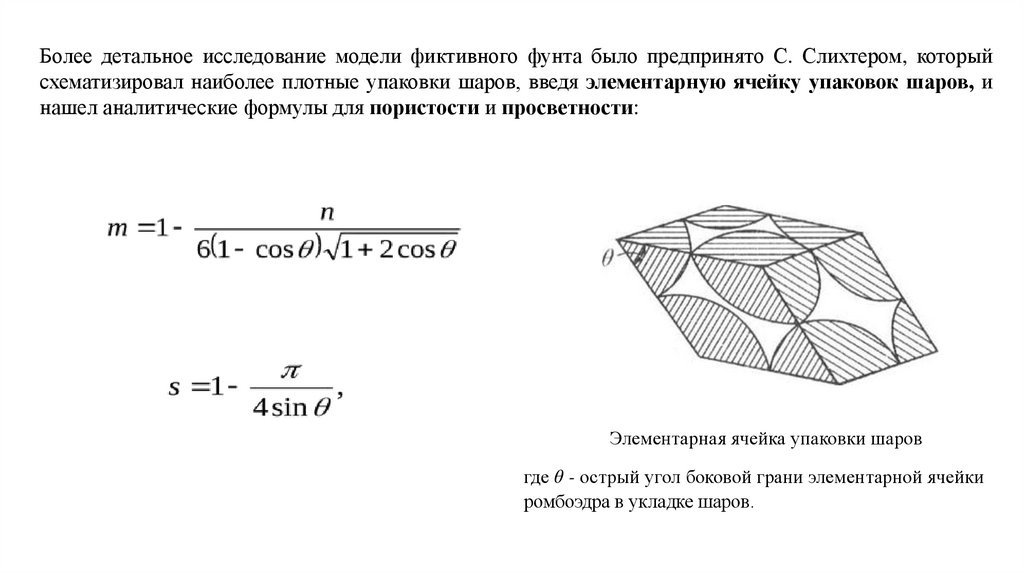
Более детальное исследование модели фиктивного фунта было предпринято С. Слихтером, который
схематизировал наиболее плотные упаковки шаров, введя элементарную ячейку упаковок шаров, и
нашел аналитические формулы для пористости и просветности:
Элементарная ячейка упаковки шаров
где θ - острый угол боковой грани элементарной ячейки
ромбоэдра в укладке шаров.

8.

Значение угла по С. Слихтеру изменяется в пределах
от 60° до 90°, и, следовательно, пористость и
просветность
изменяются
в
пределах
0,259 ≤ т ≤ 0,476 и 0,0931 ≤ s ≤ 0,2146. Как следует из
соотношений ни пористость, ни просветность не
зависят от диаметра шаров и определяются только углом θ. Поэтому, исключив из соотношений угол,
можно найти связь между пористостью и
просветностью.
К сожалению, система уравнений является
трансцендентной,
поэтому
связь
между
пористостью и просветностью задается с
помощью приближенных формул

9.

Дальнейшее развитие изучения фиктивного грунта получило в
работах И. Козени и П. Кармана, которые предложили для
вычисления проницаемости пористых сред формулу
где с — число Кармана. В результате многочисленных
экспериментальных исследований было установлено, что для
упаковок шаров число Кармана приблизительно равно 5.
Выражение для проницаемости фиктивного грунта:

10.

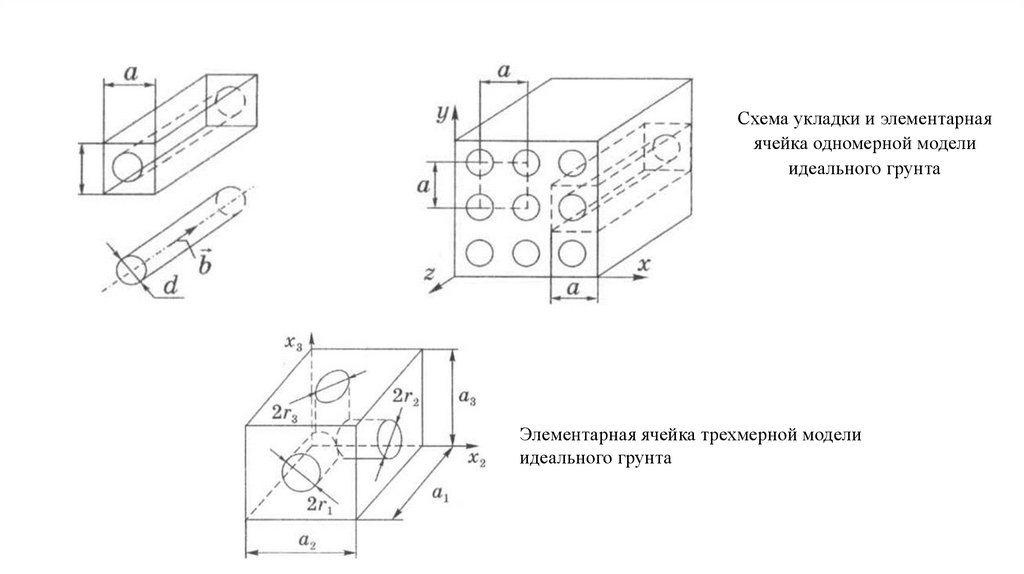
Вычислим значения пористости, просветности, удельной поверхности и проницаемости для
идеального грунта, образованного тремя системами взаимно перпендикулярных капилляров. Диаметры
капилляров примем равными dα =2rα , а периоды укладки - аα , α = 1, 2, 3.
Введем декартову систему координат, оси которой параллельны осям симметрии капилляров,
которые, в свою очередь, параллельны периодам укладки. Значения индексов в обозначении
диаметров и периодов введем следующим образом: номер а соответствует номеру оси координат,
которой параллельны капилляр и период. Тогда для пористости, просветности, удельной
поверхности и проницаемости, соответственно, получим следующие значения:

11.

Схема укладки и элементарная
ячейка одномерной модели
идеального грунта
Элементарная ячейка трехмерной модели
идеального грунта

12.

Для вычисления проницаемости рассмотрим
движение жидкости в капилляре и воспользуемся
известными
гидравлическими
соотношениями:
уравнением Бернулли для потока вязкой жидкости
и формулой Дарси-Вейсбаха для определения
потерь напора
Здесь использованы следующие обозначения: h1-2 потери напора между сечениями 1 и 2, hτ — потери
напора по длине, λ — коэффициент гидравлического
сопротивления, / - длина капилляра между сечениями
1 и 2.
Так как при фильтрации скорости очень малы, то
пренебрежем скоростными напорами, и для
вычисления коэффициента гидравлического сопротивления примем формулу для ламинарного
режима течения в круглой трубе

13.

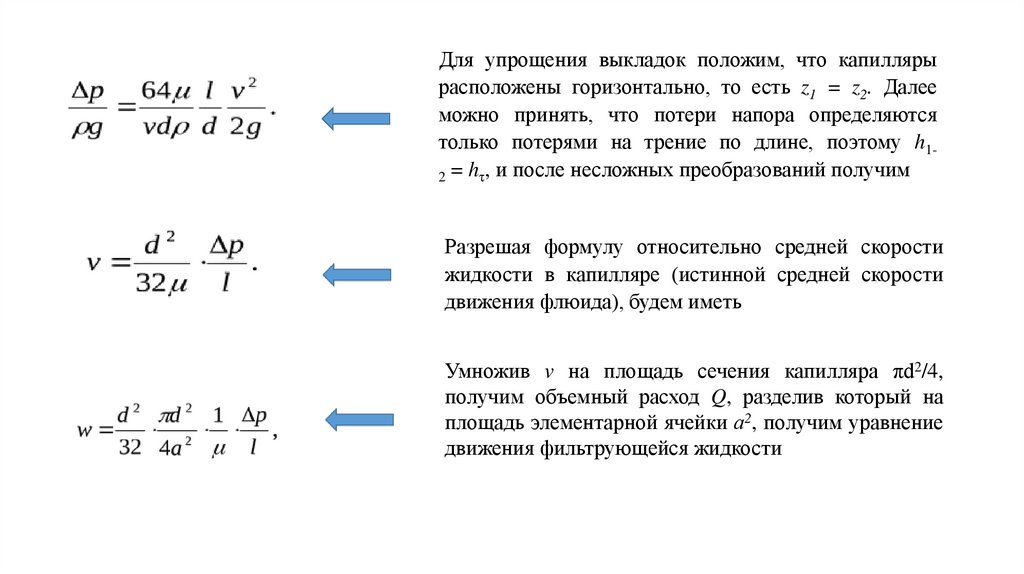
Для упрощения выкладок положим, что капилляры
расположены горизонтально, то есть z1 = z2. Далее
можно принять, что потери напора определяются
только потерями на трение по длине, поэтому h12 = hτ, и после несложных преобразований получим
Разрешая формулу относительно средней скорости
жидкости в капилляре (истинной средней скорости
движения флюида), будем иметь
Умножив v на площадь сечения капилляра πd2/4,
получим объемный расход Q, разделив который на
площадь элементарной ячейки а2, получим уравнение
движения фильтрующейся жидкости

14.

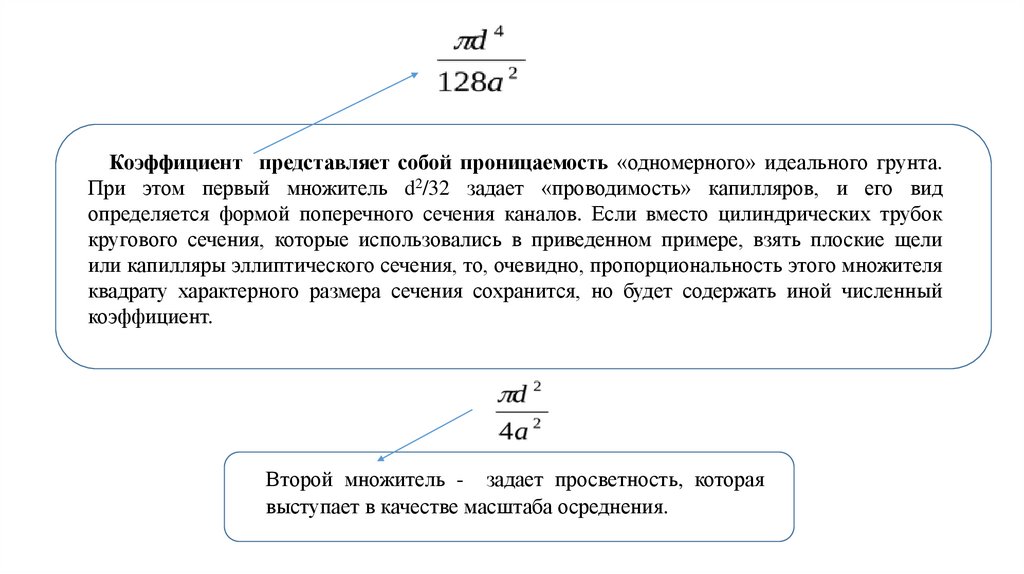
Коэффициент представляет собой проницаемость «одномерного» идеального грунта.
При этом первый множитель d2/32 задает «проводимость» капилляров, и его вид
определяется формой поперечного сечения каналов. Если вместо цилиндрических трубок
кругового сечения, которые использовались в приведенном примере, взять плоские щели
или капилляры эллиптического сечения, то, очевидно, пропорциональность этого множителя
квадрату характерного размера сечения сохранится, но будет содержать иной численный
коэффициент.
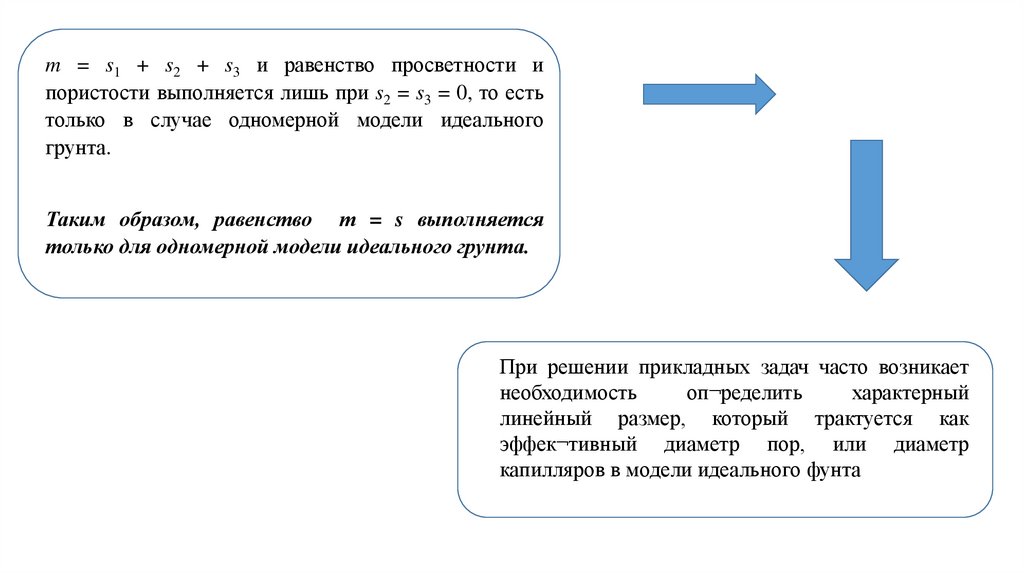
Второй множитель - задает просветность, которая
выступает в качестве масштаба осреднения.

15.

Следовательно, проницаемость является
комплексной характеристикой пористой
среды, учитывающей как форму и размеры
сечения поровых каналов, так и их
концентрацию в среде. Часто в расчетные
формулы для определения проницаемости
включают коэффициент извилистости α,
который равен отношению длины проводящего
порового канала или «истинного» пути флюида
в образце (траектории меченой частицы) к
длине образца (например, керна). В различных
модификациях модели одномерного
идеального грунта α = 1—3.
где индексы α, β, γ образуют циклическую перестановку
выражение для коэффициента проницаемости в
трехмерной модели идеальной пористой среды

16.

m = s1 + s2 + s3 и равенство просветности и
пористости выполняется лишь при s2 = s3 = 0, то есть
только в случае одномерной модели идеального
грунта.
Таким образом, равенство т = s выполняется
только для одномерной модели идеального грунта.
При решении прикладных задач часто возникает
необходимость
оп¬ределить
характерный
линейный размер, который трактуется как
эффек¬тивный диаметр пор, или диаметр
капилляров в модели идеального фунта

17.

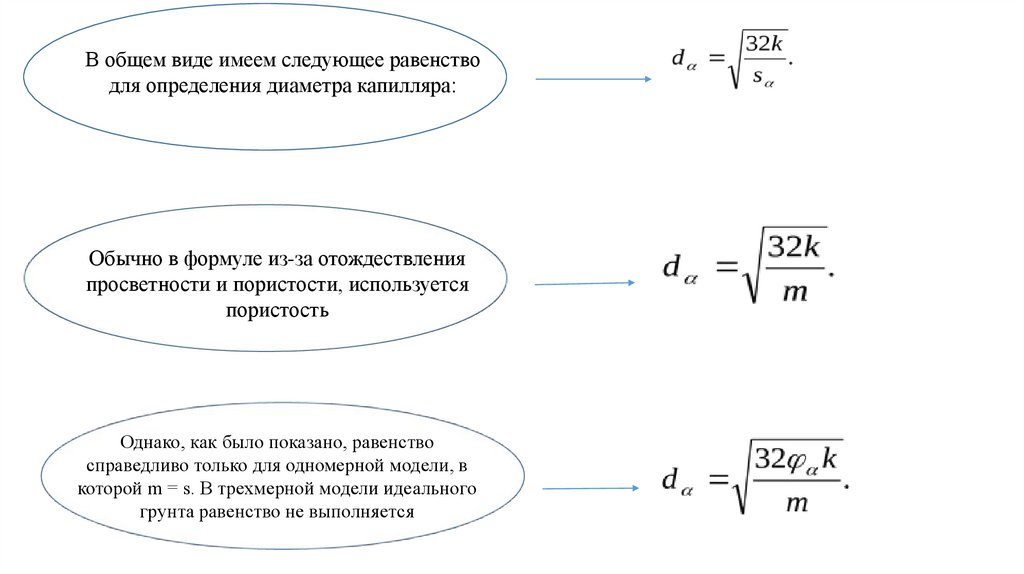
В общем виде имеем следующее равенство
для определения диаметра капилляра:
Обычно в формуле из-за отождествления
просветности и пористости, используется
пористость
Однако, как было показано, равенство
справедливо только для одномерной модели, в
которой m = s. В трехмерной модели идеального
грунта равенство не выполняется

18.

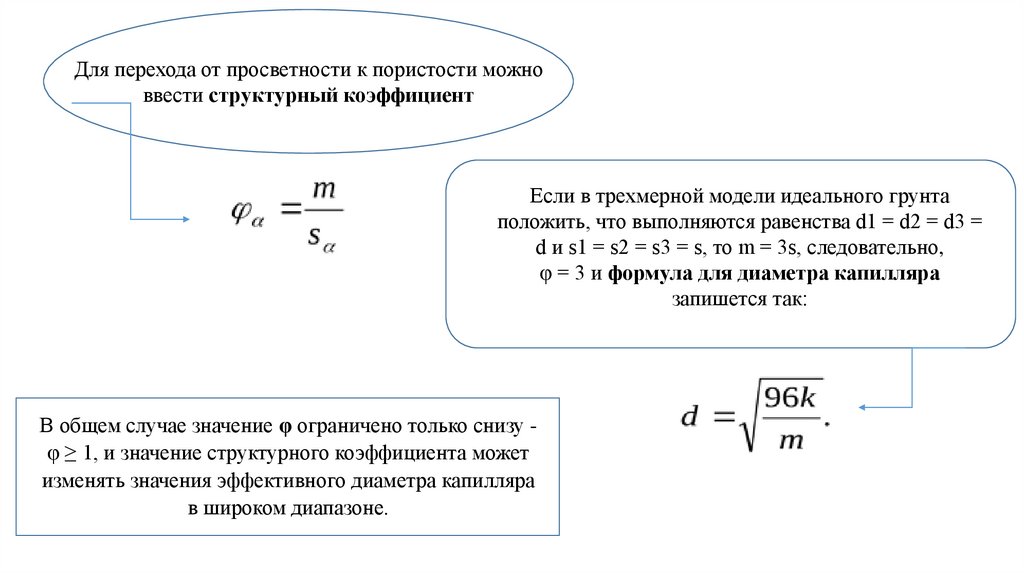
Для перехода от просветности к пористости можно
ввести структурный коэффициент
Если в трехмерной модели идеального грунта
положить, что выполняются равенства d1 = d2 = d3 =
d и s1 = s2 = s3 = s, то m = 3s, следовательно,
φ = 3 и формула для диаметра капилляра
запишется так:
В общем случае значение φ ограничено только снизу φ ≥ 1, и значение структурного коэффициента может
изменять значения эффективного диаметра капилляра
в широком диапазоне.

19.

В заключение отмечу, что были рассмотрены простейшие структурные
модели пористых сред, для которых наиболее просто вычислить
фильтрационно-емкостные характеристики с помощью геометрических и
гидравлических соотношений, не привлекая стохастических и иных методов.
В настоящее время для моделирования пористых сред используются
разнообразные статистические структурные модели с хаотично уложенными сферами, со случайными решетками и со сложной геометрией капиллярных каналов.