Похожие презентации:
Подземная гидродинамика
1.
ПОДЗЕМНАЯГИДРОДИНАМИКА
1
2.
ОСНОВНЫЕ ПОЛОЖЕНИЯПОДЗЕМНАЯ ГИДРОДИНАМИКА - наука,
изучающая движение флюидов через горные
породы, имеющие пустоты, одни из которых
называют порами, другие трещинами.
ТЕОРИЯ ФИЛЬТРАЦИИ - наука, описывающая
движение флюидов с позиций механики
сплошной среды, т.е. гипотезы сплошности
(неразрывности) течения
КОЛЛЕКТОРА - горные породы, которые могут
служить хранилищами флюидов и отдавать их
при разработке
2
3. ФИЗИЧЕСКИЕ ОСНОВЫ ПОДЗЕМНОЙ ГИДРОДИНАМИКИ
МоделиАбстрактные
Требования
процессам:
адекватности
Физические
моделей
реальным
полнота - содержание достаточного числа признаков
реального объекта;
непротиворечивость - включенные признаки не должны
противоречить друг другу;
реализуемость - построенная математическая модель
должна допускать аналитическое или численное решение,
а физическая - реализацию в искусственных условиях;
компактность и экономичность - процессы сбора
информации, подготовка и реализация модели
должны быть максимально просты, обозримы и
экономически целесообразны.
3
4.
МОДЕЛИ ФИЛЬТРАЦИИИЗОТЕРМИЧЕСКОЕ
ПРИБЛИЖЕНИЕ
СПЛОШНАЯ
СРЕДА
ПРОСТРАНСТВЕННЫЕ
ВРЕМЕННЫЕ
ПО ЧИСЛУ ФАЗ
МОДЕЛИ ФЛЮИДОВ
ПО СТЕПЕНИ
СЖИМАЕМОСТИ
РЕОЛОГИЧЕСКИЕ
xy
.u x
.y
4
5.
МОДЕЛИРОВАНИЕКОЛЛЕКТОРОВ
ГЕОМЕТРИЧЕСКОЕ
ТЕПЛО-МЕХАНИЧЕСКОЕ
ФАЗОВОЕ
5
6.
ГЕОМЕТРИЧЕСКИЕ МОДЕЛИВИДЫ
КОЛЛЕКТОРОВ
ПОРОВЫЕ
ТРЕЩИНОВАТЫЕ
СМЕШАННЫЕ
6
7.
ИДЕАЛИЗИРОВАННЫЕ МОДЕЛИПОРИСТЫХ КОЛЛЕКТОРОВ
Фиктивный
грунт
среда, состоящая из шариков
одного размера, уложенных
во всем объёме пористой
среды одинаковым образом
по элементам из восьми
шаров в углах ромбоэдра
Идеальный
грунт
среда,
состоящая
из
трубочек одного размера,
уложенных
одинаковым
образом по элементам из
четырех трубочек в углах
ромба.
7
8.
ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ ПОРИСТЫХ КОЛЛЕКТОРОВГРАНУЛОМЕТРИЧЕСКИЙ
СОСТАВ
УДЕЛЬНАЯ
ПОВЕРХНОСТЬ
ПОРИСТОСТЬ
ПРОНИЦАЕМОСТЬ
8
9.
ГРАНУЛОМЕТРИЧЕСКИЙ СОСТАВГранулометрическим составом породы
называют количественное (массовое)
содержание в породе частиц различной
крупности
Степень
неоднородности
Эффективный
диаметр
d 60
d10
3
n
d
i i
3
dэ
ni
9
10.
ГРАНУЛОМЕТРИЧЕСКИЙ СОСТАВЭффективный диаметр –
такой
диаметр
шаров,
образующих эквивалентный
фиктивный
грунт,
при
котором
гидравлическое
сопротивление,
оказываемое фильтрующейся жидкости
в
реальном
и
эквивалентном
грунте,
одинаково.
11. ГРАНУЛОМЕТРИЧЕСКИЙ СОСТАВ ПОРОДЫ
Гранулометрический состав – содержание в горной породе зеренразличной крупности, выраженное в % от массы или количества зерен
исследуемого образца.
Диапазон размеров частиц в нефтесодержащих
породах 0,01 – 1 мм
Изучаемый диапазон размеров: 0,001- 5 мм
Методы анализа
гранулометрического
состава горных пород
Ситовой анализ
Седиментационный
анализ
Микроскопический
анализ шлифов
d > 0,05 мм
0,01< d < 0,1 мм
0,002 < d < 0,1 мм
12.
ГРАНУЛОМЕТРИЧЕСКИЙ СОСТАВ ПОРОДЫСИТОВОЙ АНАЛИЗ
Ситовой анализ сыпучих горных пород применяют для определения содержания
фракций частиц размером от 0,05 до 6 - 7 мм, а иногда и до 100 мм. В лабораторных
условиях обычно пользуются набором проволочных или шелковых сит с размерами
отверстий (размер стороны квадратного отверстия) 0,053; 0,074; 0,105; 0,149; 0,210;
0,227; 0,42; 0,59; 0,84; 1,69 и 3,36 мм.
13.
ГРАНУЛОМЕТРИЧЕСКИЙ СОСТАВ ПОРОДЫСИТОВОЙ АНАЛИЗ
Интегральное распределение частиц по размерам
14.
ГРАНУЛОМЕТРИЧЕСКИЙ СОСТАВ ПОРОДЫСедиментационный анализ
Седиментационное разделение частиц по
фракциям происходит вследствие различия
скоростей оседания зерен неодинакового
размера в вязкой жидкости. По формуле Стокса
скорость осаждения в жидкости частиц
сферической формы
gd 2 п
v
1
18 ж
C глубины h через время tx в
пипетку проникнут только те
частицы, диаметр которых меньше
d1 так как к этому времени после
начала их осаждения более крупные
зерна расположатся ниже кончика
пипетки.
V1G
a
VG1
15.
ГРАНУЛОМЕТРИЧЕСКИЙ СОСТАВ ПОРОДЫВесовой седиментометр ВС - 3
для автоматизированного анализа
гранулометрического состава
порошков металлов, сплавов,
органических и неорганических
соединений
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
Диапазон измеряемых размеров частиц..2 – 300 мкм
Время анализа одной пробы..10 – 120 мин
Вес анализируемой пробы……20 – 40 мГ
Количество анализируемых проб …до 20
(без смены седиментационной жидкости)
Чувствительность системы измерений 0,1 мГ
Объем седиментационной жидкости…2 Л
(дистиллированная вода)
Вес прибора (без компьютера)... до 6 кГ
16.
ПОРИСТОСТЬПОЛНАЯ
mп = Vп/V
ОТКРЫТАЯ
mот = Vоткр/V
ДИНАМИЧЕСКАЯ
mдин = Vдинам/V
УДЕЛЬНАЯ ПОВЕРХНОСТЬ Sуд - суммарная площадь поверхности частиц, содержащихся в единице объёма
Среднее значение Sуд для нефтесодержащих пород
изменяется в пределах 40тыс. - 230тыс.м2/м3.
16
17. УДЕЛЬНАЯ ПОВЕРХНОСТЬ ГОРНЫХ ПОРОД
Удельной поверхностью пород называется суммарная поверхностьчастиц или поровых каналов, содержащихся в единице объема образца.
F 4 r
Поверхность одной песчинки равна
Для фиктивного грунта число песчинок в единице
объема породы равно
N
2
Объем
1 m
4
3
r 3
3 1 m
3
4 r
3(1 m )
S
r
Суммарная поверхность всех песчинок в
единице объема породы равна
Для песчинок радиусом г = 0,1 мм, удельная поверхность будет равна (если
2
пористость m = 0,26)
3
3 ( 1 0.26 )
4м
S (1 m )
r
10
4
2.2 10
В 1 м3 песка общая поверхность частиц с радиусом 0,1 мм составит 22000 м2.
Удельная поверхность частиц с радиусом 0,05 мм составит уже 44 000 м2/м3
м3
18.
ПРОНИЦАЕМОСТЬпараметр
породы,
характеризующий её способность пропускать к забоям
скважины флюиды.
Проницаемость измеряется: в системе СИ - м2;
технической системе - дарси (д);
1д=1,02мкм2=1,02 .10-12м2.
Физический смысл проницаемости k заключается в
том, что проницаемость характеризует площадь сечения
каналов пористой среды, по которым происходит
фильтрация.
ВИДЫ ПРОНИЦАЕМОСТИ
АБСОЛЮТНАЯ
ОТНОСИТЕЛЬНАЯ
k
ФАЗОВАЯ (ЭФФЕКТИВНАЯ)
ki
ki
18
19.
Проницаемость абсолютная (физическая) –проницаемость пористой среды для газа или
однородной жидкости при следующих
условиях:
1. Отсутствие физико-химического
взаимодействия между пористой средой и
этим газом или жидкостью.
2. Полное заполнение всех пор среды этим
газом или жидкостью.
Проницаемость фазовая (эффективная) –
проницаемость пористой среды для данного
газа или жидкости при одновременном
наличии в порах другой фазы или системы.
Относительная проницаемость – отношение
фазовой проницаемости к абсолютной.
ki
ki
k
19
20. Измерение проницаемости по газу
КерндержательQ
Расходомер
Газ
Датчики давления
Образец керна
P1
P2
∆P = P1 – P2
Компрессор
21. Размерность проницаемости
q – объемный расход; [q] = м3 / сμ – вязкость жидкости; [μ] = Па∙с
∆p – перепад давления; [∆p] = Па
L – длина образца пористой среды; [L] = м
A – площадь поперечного сечения образца; [A] = м2
q L
k
A p
L3 P T L 1 1
k
2 L2
1 1 P L
T
В системе СИ [k] = м2.
Внесистемные единица – Дарси (1Д)
Часто используют производную единицу – мкм2
22.
ИДЕАЛИЗИРОВАННЫЕ МОДЕЛИТРЕЩИНОВАТЫХ КОЛЛЕКТОРОВ
Рис.1.3. Схема одномерной Рис.1.4 Схема пространственной
модели трещиноватой среды
модели трещиноватой среды
22
23.
ТРЕЩИНОВАТЫЕ ПОРОДЫПАРАМЕТРЫ
ТРЕЩИНОВАТОСТЬ
отношение
объёма
трещин Vт ко всему
объёму V трещинной
среды.
mт
Vт
V
ГУСТОТА
отношение полной
длины li всех
трещин,
находящихся
в
данном
сечении трещинной
породы к удвоенной
площади сечения f
li 1
Гт
.
2f м
РАСКРЫТОСТЬ
т
Ширина
трещины
mт= Гт т
*
т т0 1 т р0 р
23
24.
ТЕПЛО- МЕХАНИЧЕСКИЕ ПАРАМЕТРЫДЕФОРМАЦИОННЫЕ И ПРОЧНОСТНЫЕ
СВОЙСТВА ГОРНЫХ ПОРОД
ДЕФОРМАЦИЯ:
1. УПРУГАЯ ( S);
2. ПЛАСТИЧЕСКАЯ( S);
3. КРИП (ПОЛЗУЧЕСТЬ) -
постепенное нарастание
деформации при
постоянном напряжении.
4. ХРУПКАЯ
24
25.
ТЕПЛОВЫЕ СВОЙСТВАГОРНЫХ ПОРОД
ОСНОВНЫЕ ПАРАМЕТРЫ
УДЕЛЬНАЯ
ТЕПЛОЁМКОСТЬ
КОЭФФИЦИЕНТ
с
ТЕПЛОПРОВОДНОСТИ
T
dQ
Sdt
x
С = 0,4 - 2 кДж/(кг К).
УДЕЛЬНОЕ ТЕПЛОВОЕ
СОПРОТИВЛЕНИЕ
КОЭФФИЦИЕНТ
ТЕМПЕРАТУРОПРОВОДНОСТИ
a
c
25
а
26.
ЗАКОНЫ ФИЛЬТРАЦИИПОРИСТАЯ СРЕДА
СКОРОСТЬ ФИЛЬТРАЦИИ
u w m
Физический смысл введения скорости фильтрации заключается
в том, что рассматривается некоторый фиктивный поток, в котором
расход через любое сечение равен реальному расходу, поля
давлений фиктивного и реального потоков идентичны, а сила
сопротивления фиктивного потока равна реальной.
ЗАКОН ДАРСИ (ЛИНЕЙНЫЙ
ЗАКОН ФИЛЬТРАЦИИ)
k
*
u gradp
26
27.
ГРАНИЦЫ ПРИМЕНИМОСТИ ЗАКОНАДАРСИ
wa
Re
ВЕРХНЯЯ ГРАНИЦА
ЧИСЛО РЕЙНОЛЬДСА
Формула
Щелкачева
Re
10u k
m
2, 3
где а = 10 k
НИЖНЯЯ ГРАНИЦА
,
m
Reкр=1-12
2, 3 ;
w=u .
dp
u ’ , u 0,
dl k
dp
н ,
u 0.
dl
27
28.
НЕЛИНЕЙНЫЕ ЗАКОНЫФИЛЬТРАЦИИ
СТЕПЕННОЙ
1
n
dp
u C
, 1 n 2
dl
ДВУХЧЛЕННАЯ
ЗАВИСИМОСТЬ
dp
2
Au Bu .
dl
5 2
12
10
d
A ; B ,
.
k
k
mk
28
29.
ТРЕЩИНОВАТАЯ СРЕДАСКОРОСТЬ ФИЛЬТРАЦИИ
dp
w
.
12 dl
2
т
ЗАКОН ДАРСИ
u w mT
- Формула Буссинеска
kT
*
u gradp
т Гт
kт
.
12
3
т
Для трещиновато-пористой среды общая проницаемость
определяется как сумма межзерновой и трещинной
проницаемостей
Зависимость проницаемости
от давления
4u 3k т
Re КР
mт mт
kТ kТ 0 1 p0 p . Re
*
3
КР=0-4.
29
30.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯФИЛЬТРАЦИИ
при отсутствии источников - стоков
1. Уравнение неразрывности
m
div u 0
t
2. Уравнение движения в форме Дарси
k
u gradp*
где р*=р+z g, u=dG/dt, G - расход массы жидкости в
единицу времени через поверхность равного потенциала (массовый
дебит); среда изотропна.(k=const,
=const)
f
f y f z grad
i+
j+
k
x
div f
;
x
y
z
30
x y z
31.
Уравнения потенциального движенияПОТЕНЦИАЛ
k
dp C
ЗАКОН ДАРСИ
u grad
m
t
0
УРАВНЕНИЯ ЛАПЛАСА
Несжимаемая
жидкость
div grad 2 2 2
x y
z
2
2
2
31
32.
Свойства уравнения Лапласа, имеющие большое практическоеприложение:
сумма частных решений является также решением уравнения
Лапласа;
произведение частного решения на константу - также решение.
Уравнения фильтрации для
трещиновато-пористой среды
Характерные особенности :
1) состоит из двух сред с порами разных масштабов
(среда 1 - роль поровых каналов играют трещины, а роль
зёрен - пористые блоки; среда 2 - обычная пористая
среда, образующая блоки);
2) между отмеченными средами при фильтрации
возникает переток жидкости из пористых блоков в
трещины в пределах выделенного элементарного объёма
трещиновато-пористого пласта.
32
33.
Для трещинДля блоков
1m т
div 1u1 q1, 2
t
2mп
div 2u 2 q1, 2
t
Здесь q1,2 - масса жидкости, поступающей из пористых блоков
в трещины за единицу времени на единицу объёма с
размерностью МL-3T-1, где М – размерность массы, L –
расстояния и Т – времени; q1,2= ( 2 - 1), .
33
34.
Начальные и граничные условияНачальные условия = о(x,y,z) при t=0
Если при t=0 пласт не возмущён, то = о=const.
Граничные условия
Внешняя граница :
1)постоянный потенциал (Г,t)= к=const - контур питания;
2) постоянный расход G=F u=const или
3) переменный поток массы через границу
const;
n
4) замкнутая внешняя граница
5) бесконечный пласт limx (Г,t)= к=const
y
34
35.
Внутренняя граница1) постоянный потенциал (rc , t)= c=const
2) постоянный массовый дебит
G
G uf c 2 rch
const или r
при r rc
r
r 2 h
3) переменный потенциал на забое
4) переменный массовый дебит
5) не работающая скважина
35
36.
Замыкающие соотношенияЗависимость плотности
от давления или уравнения
состояния
а) Несжимаемая - =соnst
с р р 0
в) Упругая
0e
где ж - коэффициент объёмного расширения, , Vж - объём
жидкости; ж= (7-30)10-10 Па-1- для нефти и (2,7-5)10-10Па-1 для
пластовой воды.
с) Сжимаемая . р= R T ; рпл < 9 МПа; р < 1 МПа
р=z R T; рпл > 9 МПа
где R - газовая постоянная, Т - температура, z - коэффициент
сверхсжимаемости.
36
37.
Зависимость пористости от давленияэф+рпл=ргорн=const
m m 0e
m р р 0
Зависимость вязкости и проницаемости
от давления
0e
a р р 0
k k 0e
ak р р 0
37
38.
Установившаяся потенциальная одномернаяфильтрация
ВИДЫ ОДНОМЕРНЫХ ПОТОКОВ
38
39. Описание одномерных потоков
1.Прямолинейно-параллельный поток.Траектории всех частиц жидкости параллельные прямые, а скорости фильтрации
во всех точках любого поперечного
(перпендикулярного к линиям тока) сечения
потока равны между собой, поверхности равных
потенциалов (эквипотенциальные поверхности)
и поверхности равных скоростей (изотахи)
являются плоскими поверхностями
перпендикулярными траекториям. Законы
движения вдоль всех траекторий такого
фильтрационного потока идентичны, а потому
достаточно изучить движение вдоль одной из
траекторий, которую можно принять за ось
координат - ось х.
39
40. Описание одномерных потоков
2. Плоскорадиальный поток. Траектории всехчастиц жидкости - прямолинейные
горизонтальные прямые, радиально
сходящиеся к центру скважины, а скорости
фильтрации во всех точках любого поперечного
(перпендикулярного к линиям тока) сечения
потока параллельны и равны между собой;
изотахи и эквипотенциальные поверхности
перпендикулярны траекториям и образуют
цилиндрические окружности с осью,
совпадающей с осью скважины. Схемы линий
тока в любой горизонтальной плоскости потока
будут идентичными и для характеристики
потока достаточно рассмотреть движение
жидкости в одной горизонтальной плоскости.
40
41. Описание одномерных потоков
3. Радиально-сферический поток. Траекториивсех частиц жидкости - прямолинейные
горизонтальные прямые, радиально
сходящиеся к центру полусферического забоя;
изотахи и эквипотенциальные поверхности
перпендикулярны траекториям и образуют
сферические поверхности. Скорость
фильтрации в любой точке потока является
функцией только расстояния этой точки от
центра забоя. Следовательно, этот вид
фильтрационного потока также является
одномерным.
41
42.
ИССЛЕДОВАНИЕ ОДНОМЕРНЫХТЕЧЕНИЙ
Задача
исследования
установившегося
фильтрационного потока заключается в определении
дебита (расхода), давления, градиента давления и
скорости фильтрации в любой точке потока, а также в
установлении закона движения частиц жидкости (или
газа) вдоль их траекторий и в определении
средневзвешенного
по
объёму
порового
пространства пластового давления.
42
43.
Решение общегодифференциального уравнения
Показатель формы потока
Начало системы координат:
• галерея (для прямолинейно- параллельного потока);
• центр контура скважины в плоскости подошвы
пласта (для плоско-радиального потока);
• центр полусферического забоя скважины (для
радиально-сферическиого потока).
Для укрупнённой трубки тока u= G/F( r ),
где F=F( r ) - площадь эквипотенциальной поверхности
прямолинейно-параллельный поток - F(r) = Bh;
плоскорадиальный поток
- F(r) = 2 hr;
радиально-сферический поток
- F(r) = 2 r2.
G>0 - эксплуатационная скважина
43
44.
Уравнение Дарси через расходd G
j
dr Ar
прямолинейно-параллельный поток - A=Bh, j=0;
плоскорадиальный поток
- A =2 h, j=1;
радиально-сферический поток
- A = 2 , j=2.
j - показатель формы потока, т.к. характеризует вид одномерного
течения.
1 j
Уравнение для потенциала
(j=0;2)
Уравнение для потенциала
(j=1)
G r
C
A 1 j
G
ln r C
2 h
Выражение для С при задании потенциала на контуре
44
45.
Уравнение для потенциала(j=0;2)
d
G
j
dr
Ar
d
G
dr
j
Ar
G
d
dr
j
Ar
G 1
j dr
A r
G
1 j
r С
A(1 j )
45
46.
Уравнение для потенциала(j=1)
d
G
j
dr
Ar
d
G
2 h
G
dr
2 hr
1
dr
r
G
ln r С
2 h
46
47.
Выражение для дебита при постоянных потенциалах награницах (j=0;2)
G
r 1 j C
A(1 j )
G
G
1 j
1 j
K
rK C; C
rC C
A(1 j )
A(1 j )
G
G
1 j
1 j
K C
rK
rC
A(1 j )
A(1 j )
G
1 j
1 j
K C
(rK rC )
A(1 j )
( K C ) A(1 j )
G
1 j
1 j
rK rC
47
48.
Выражение для дебита при постоянных потенциалах награницах (j=1)
K
G
G
ln rK C ;
C
ln rC C
2 h
2 h
G
G
K C
ln rK
ln rC
2 h
2 h
G
K C
(ln rK ln rC )
2 h
G
rK
K C
ln
2 h rC
( K C )2 h
G
rK
ln
48
rC
49.
Выражение для дебита при постоянных потенциалахна границах
1 j
G A
1 j
к
r
c
к
r
(j=0;2)
1 j
c
к с
,
; G 2 h
rк
ln
(j=1)
rc
к a rк1 j r 1 j ,
Уравнение для потенциала
(j=0;2)
к с
где a 1 j 1 j
rк rс
rк
к a ln
,
r
Уравнение для потенциала
к с
где a
(j=1)
rк
ln
r
49
50.
GG
1 j
1 j
r C; K
rK
C
A(1 j )
A(1 j )
G
1 j
K
(rK r 1 j )
A(1 j )
G
1 j
K
(rK r 1 j )
A(1 j )
( K C ) A(1 j )
G
1 j
1 j
rK rC
( K C )
1 j
1 j
K 1 j
(
r
r
)
K
1 j
rK rC
50
51.
GG
ln r C
K
ln rK C ;
2 h
2 h
G
G
K
ln rK
ln r
2 h
2 h
G
rK
G
ln
K
(ln rK ln r ) K
2 h
r
2 h
G
rK
( K C )2 h
G
K
ln
;
rK
2 h
r
ln
rC
( K C ) rK
K
ln
rK
r
ln
rC
51
52.
kПОТЕНЦИАЛЬНЫЕ ФУНКЦИИ
dp C
Несжимаемая жидкость пористый пласт (k=const, =const)
k
p C
Несжимаемая жидкость трещиноватый пласт ( =const)
4
k
*
1 р0 р C
*
4
0
m
k k 1 р 0 р
0
m
*
3
* ~ 10 6
10 7 м 2 / н
52
53.
kdp C
Упругая жидкость пористый пласт (k=const)
k
С
ж
0e
ж р р 0
Совершенный газ, пористый пласт (k=const, = cт р/ рст. )
k ст 2
р С
2 p ст
53
54.
kdp C
Реальный газ, пористый пласт (k=const)
р z(p ст )
ст
р ст z(p )
k ст
f (p ) C
p ст
f (p) (p)z(p) pdp
1
p2
f
C
2 z
54
55.
АНАЛИЗ ПРИТОКА НЕФТИ К СКВАЖИНЕ ПО ЗАКОНУ ДАРСИИСХОДНЫЕ УРАВНЕНИЯ
ИЗМЕНЕНИЯ ПОТЕНЦИАЛЬНОЙ ФУНКЦИИ
к rк
к
ln , к к с ; rк rк
rс
ln rк r
ПРИТОКА
к
G 2 h
;
ln rк
ИЗМЕНЕНИЕ ГРАДИЕНТА ПОТЕНЦИАЛА
d 1 к
dr r ln rк
55
56.
ПОРИСТЫЙ ПЛАСТk
p С
ПОТЕНЦИАЛ
rк
рк
, где a1
;
РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЯ р рк a1 ln
r
ln rк
2 hk
2 hk рк
a1
ОБЪЁМНЫЙ ДЕБИТ (ФОРМУЛА ДЮПЮИ) Q
ln rк
ГРАДИЕНТ ДАВЛЕНИЯ
d р а1
;
dr
r
СКОРОСТЬ ФИЛЬТРАЦИИ
u Q
k 1
a1 ;
2 hr r
56
57.
ЗАКОН ДВИЖЕНИЯ ЧАСТИЦ ФЛЮИДАУравнение движения
ВРЕМЯ ДВИЖЕНИЯ
Время отбора всей
жидкости из
кругового пласта
dr
Q
dt 2 mhr
mh R 02 r 2
t
Q
mh r r
T
Q
Средневзвешенное давление
~
р рк а1
2
к
2
с
1
~
р
р dVпор
Vпор
Vпор rк2 rc2 h m;
dVпор 2 h m r dr
57
58.
Коэффициент продуктивности скважиным3
Q c
K
p к Па
58
59.
Анализ:1. Дебит не зависит от r, а только от депрессии рк. График
зависимости Q от рк называется индикаторной диаграммой,
а сама зависимость - индикаторной.
2. Градиент давления и, следовательно, скорость фильтрации u
обратно пропорциональны расстоянию r и образуют гиперболу с
резким возрастанием значений при приближении к забою.
3. Графиком зависимости р=р(r) является логарифмическая
кривая, вращением которой вокруг оси скважины образуется
поверхность, называемая воронкой депрессии.
4. Изобары - концентрические, цилиндрические поверхности,
ортогональные траекториям.
5. Дебит слабо зависит от величины радиуса контура rк для
достаточно больших значений rк /rc, т.к. rк /rc входят в формулу
под знаком логарифма.
59
60.
ТРЕЩИНОВАТЫЙ ПЛАСТПОТЕНЦИАЛ
k 0т
4
*
1 р
РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЯ
*
C
1 4
р рк
,
а2
rк
где 1
ln ,
ln rк r
.
ГРАДИЕНТ ДАВЛЕНИЯ
к р
4
4
*
а 2 1 1 р к
d р а2
1
;
dr 4r ln r 1 * p р 3
к
к
60
61.
Объёмный дебитhk
Q
a2
*
2 ln rк
Скорость фильтрации
Кривые распределения
давления
1- недеформируемый
пласт
2 - трещиноватый пласт
0
т
u Q
k
1
a2 ;
*
2 hr 4
r
Вид индикаторной кривой
при фильтрации несжимаемой жидкости в трещиноватом пласте
61
62.
1. Воронка депрессии для трещиноватого пласта болеекрутая, чем для пористого. Более резко снижается
давление в пласте с большим *.
2. Индикаторная кривая - парабола четвёртого порядка с
координатами вершины
hk 0
1
Q
т
*
2 ln rк
; рс
3. Комплексный параметр * можно определить
взяв по индикаторной кривой два известных
значениях дебита Q1 и Q2 при двух значениях
депрессии рс1 , рс2 , т.е. из соотношения
*
Q 1 1 1 p c1
Q 2 1 1 * p
c2
4
4
62
63.
Потенциальное движение упругой жидкостичерез недеформируемый пласт
k
С
ж
Для упругой жидкости зависимость между и координатой r
выражается точно теми же формулами, какими выражается
зависимость между р и r для несжимаемой жидкости
Для малых перепадов давления ~ p, а не ер
Индикаторная зависимость
2 h к
G
;
ж ln rк
63
64.
Течение совершенного газа черезнедеформируемый пласт
k ст 2
р С
2 pcт
2
р
rк
2
2
к
р рк
ln ,
ln rк r
где р к2 р к2 р с2 .
Распределение давления в
недеформируемом пласте
1 - газ; 2 несжимаемая жидкость
Пьезометрическая кривая для газа
имеет более пологий характер на
большем своём протяжении, чем
кривая несжимаемой жидкости;
однако у неё более резкое
изменение у стенки скважины, чем
для несжимаемой жидкости.
64
65.
Уравнение притокаhk ст р к2
G
.
р ст ln rк
или
Индикаторная
зависимость при
фильтрации газа по
закону Дарси
hk р к2
Q ст
.
р ст ln rк
Qст 2 рк рк рк
2
т.к. рк2 - рс2 = 2рк рс - ( рс)2
(где рс= рк - рс )
Индикаторная
зависимость
для
газа
-параболическая зависимость дебита Qст от
депрессии рк и линейная зависимость дебита от
разницы квадратов пластового и забойного 65
давлений.
66.
Распределение градиента давления2
pк
dp 1
dr rр 2 ln rк
Градиент давления вблизи забоя
резко возрастает как за счёт
уменьшения r, так и за счёт
падения давления р, вызванного
сжимаемостью газа.
Изменение скорости фильтрации
2
k pк
1
u
rр 2 ln rк
Скорость фильтрации слабо
меняется вдали от скважины и
резко возрастает в призабойной
зоне
66
67.
Течение реального газа черезнедеформируемый пласт
Потенциальная функция
рпл>10МПа;
рс/рк<0.9.
k ст р 2
C
p ст 2 z
2
hk
р
к
Уравнение притока Q ст
,
z р ст ln rк
где Qст=G/ cm
Дебиты реального газа ниже дебитов совершенного
при тех же условиях.
Для тяжелых углеводородов дебит природного газа может
составлять всего лишь 72% дебита совершенного.
67
68.
Анализодномерных потоков
нелинейных законах фильтрации
при
dp
2
u bu
dr k
где
b
k
68
69.
Течение несжимаемая жидкости в недеформируемомпласте
2
dp Q
Q
b
2
dr k 2 rh
2 rh
Уравнение фильтрации
при u=Q / (2 rh)
Распределение давления в
пласте
р р
к
Q
Rк
Q 2b 1 1
ln
2
2 kh
r 2 h r R к
Q
Rк
Q 2b 1
1
рк рс
ln
2
2 kh rс 2 h rс R к
Уравнение притока
69
70.
Дебит - положительный корень квадратногоуравнения.
Индикаторная линия - парабола.
Кривая распределения давления - гипербола
и воронка депрессии - гипербола вращения.
Крутизна воронки депрессии у стенки
скважины
больше,
чем
у
чисто
логарифмической кривой при течении по
закону Дарси.
70
71.
Идеальный газ в недеформируемом пластеУравнение
фильтрации
pст
стpст
dp
2
Qст 2 2
Qст
2
dr 2 khpr
4 h kpr
т.к
u
стQ ст
Q p
G
ст ст
f p 2 rh 2 rhp
ст
p ст
Распределение
стp ст 2 1 1
r
2
2 p ст
давления р р с
Qст ln 2 2
Qст
kh
rc 2 h k
rc r
Распределение давления отличается от распределения
давления по закону Дарси наличием последнего члена,
что диктует более резкое изменение давления в
призабойной зоне.
71
72.
Уравнениепритока
pст
стpст
Rк
2
р р
Qст ln
2 2
Qст
kh
rc 2 h rc k
2
к
2
с
2
рк2 рс2 АQ ст ВQст
. Коэффициенты А и В определяют по данным
исследования
газовых
установившихся режимах.
скважин
при
72
73.
Однородная несжимаемая жидкость вдеформируемом (трещиноватом) пласте
р
2
Закон
a u b u ,
фильтрации l
где
a 1
b
kт
;
1,69l бл
120 1 m т k т
Закон фильтрации в дифференциальной форме через
потенциал
1,69 l бл
d т
G
G2
,
2
dr
2 hr 120 1 m т 2 hr
где
k т
т
dp C
73
74.
Уравнение притока через потенциалтк
1,69 l бл
G
rк
G2 1 1
тс
ln
2
2 h rc 120 1 m т 2 h rc rк
Уравнение притока через давление и объемный дебит
1 1 р
4
к
1,69 lбл
2 Q rк
Q2 1 1
ln
2
0
0
hkm rc 120 kт 1 mт h rc rк
Индикаторная кривая - результат сложения двух парабол:
параболы
четвёртого
порядка,
симметричной
относительно оси, параллельной оси дебитов, и параболы
второго порядка (относительно дебита Q) симметричной
относительно оси, параллельной оси депрессий ( рс) и
отстоящей от последней.
74
75.
Идеальный газ в деформируемом (трещиноватом)пласте
Закон фильтрации в дифференциальной форме
через потенциал
2
1,69 l бл
d т
G
G
2
dr
2 hr 120 1 m т 2 hr
Уравнение притока через давление и объемный
дебит
k 0т p к
1
рк
4
4
1 рк
1 1 р к
2
p ст 4 20
5
1,69 l бл Q 2 1 1
Q rк
ln
2
2 h rc 120 1 m т h rc rк
75
76.
ФИЛЬТРАЦИЯ В НЕОДНОРОДНЫХ СРЕДАХПласт называется макронеоднородным, если
его
фильтрационные
характеристики
(проницаемость,
пористость)
значительно,
скачкообразно отличаются в разных областях.
Виды макронеднородности
Слоистая
Зональная
Общая
76
77.
СЛОИСТАЯ НЕОДНОРОДНОСТЬМногослойный пласт - неоднородность по
толщине пласта.
Пропластки - гидравлически изолированы,
либо гидравлически сообщающиеся.
В
пределах
каждого
пропластка
фильтрационные параметры постоянны, а на
границе соседних они претерпевают скачок.
Если течение потенциально, то полный дебит
пласта определяется как сумма дебитов всех
пропластков.
Квазиоднородное приближение:
k cp
k ihi
h
i
77
78.
ЗОНАЛЬНАЯ НЕОДНОРОДНОСТЬПласт по площади состоит из нескольких зон
различных
фильтрационных
параметрах,
на
границах которых данные параметры меняются
скачкообразно.
Массовый дебит постоянен и равен:
а)при прямолинейно
b) при плоскорадиальном
-параллельном потоке
потоке
к с
к с
G 2 h
G Вh
1
ri
li
ln
k
ri 1
i ki
i
i
Квазиоднородное
приближение:
k cp
L
li
k
i
i
ln
k cp
Rк
rc
1
ri
ln
ri 1
i ki
78
79.
ДВУХЗОНАЛЬНЫЙ ПЛАСТ1) Ухудшение проницаемости призабойной
зоны сильнее влияет на дебит, чем
увеличение проницаемости в этой зоне.
2) В случае фильтрации по закону Дарси
увеличивать проницаемость призабойной
зоны более чем в 20 раз не имеет смысла,
т.к. дальнейшее увеличение проницаемости
практически не ведёт к росту дебита.
3) Нарушение в пластовых условиях закона
Дарси усиливает положительное влияние
увеличенной проницаемости призабойной
зоны на производительность скважины.
79
80.
ПЛОСКИЕ ЗАДАЧИТЕОРИИ ФИЛЬТРАЦИИ ОБ
УСТАНОВИВШЕМСЯ ПРИТОКЕ К
СКВАЖИНЕ
80
81.
ПРИНЦИПСУПЕРПОЗИЦИИ
При совместном действии в пласте нескольких стоков
(эксплуатационных скважин) или источников (нагнетательных
скважин) потенциальная функция, определяемая каждым стоком
(источником), вычисляется по формуле для единственного стока
(источника).
Потенциальная
функция,
обусловленная
всеми
стоками
(источниками), вычисляется путём алгебраического сложения этих
независимых друг от друга значений потенциальной функции.
Суммарная скорость фильтрации определяется как векторная
сумма скоростей фильтрации, вызванная работой каждой
81
скважины
82.
Потенциал скважины приплоскорадиальном потоке
Gi
i
ln ri Ci
2 h
Потенциал группы скважин
1
по принципу суперпозиции i 2 h G i ln ri C
Уравнение эквипотенциальных
поверхностей
Уравнение эквипотенциальных
поверхностей при равенстве
дебитов
Gi
i
r
i
sign( G i )
i
r
i
C1
C1
Линии тока образуют семейство кривых, ортогональных изобарам
82
83.
МЕТОД ОТОБРАЖЕНИЯ ИСТОЧНИКОВ (СТОКОВ) - для выполнения тех или иных условий на границах вводятся фиктивные стокиили источники за пределами пласта
Приток к совершенной скважине
Фильтрационный поток от нагнетательной
скважины к эксплуатационной
Исходная формула
1
G i ln ri C
2 h
Для данной постановки
Схема расположения
источника 01 и стока 02
G
G
G r1
ln r1
ln r2 C
ln C
знаки дебитов: источник G 1= - G, а
2 h
2 h
2 h r2
сток G 2= + G.
83
84.
Уравнение изобарr1
C1
r2
Линии изобар
- окружности
центры которых расположены
на прямой, проходящей через
центры скважин
Семейство
линий
тока
ортогонально изобарам и тоже
окружности. Все линии тока
проходят через сток и источник.
Центры всех окружностей линий
тока расположены на прямой,
делящей
расстояние
между
стоком и источником пополам
84
85.
h н эG
, т.к. на контуре эксплуатационной скважины
2a
ln
r1 rc
а на контуре нагнетательной
rc
, скважины
r1 2а
r2 2a
r2 rc
Массовая скорость фильтрации в любой точке
пласта М находится по правилу суперпозиции
сложения векторов скорости от действия
источника и стока
Ga
u
hr1r2
Время движения частицы от некоторой точки
х0 до точки х
3
3
hm x x 0
2
2
t
ax ax0
Qa 3
85
86.
Время обводнения Т (х=0; х0=2а)4 hma 2
T
3 Q
Площадь обводнения из равенства объёмов TQ и mh .
4 2
а
3
Расстояние, пройденное частицей за время Т от
нагнетательной скважины до эксплуатационной,
вдвое больше расстояния пройденного другой
частицей за это же время в положительном
направлении оси х.
86
87.
Приток к группе скважин с удаленнымконтуром питания
Дебиты из системы уравнений
n
1
сi
G i ln rci G j ln rji C
2 h
j 1, i j
1 n
к
G j ln rк C
2 h j 1
Схема группыскважин в
пласте с удаленным
контуром питания
Результат тем точнее, чем
дальше точка отстоит от
контура питания.
87
88.
Приток к скважине в пласте спрямолинейным контуром питания
МЕТОД - отображения источника и
стока
Исходная формула
1
G i ln ri C
2 h
Граничные условия: = к при r1=r2 ,т.е. при r1/r2=1;
= с при r1=rс , r2 2а, т.е. при r1/r2 rс /2а;
2 h к с
G
2a
ln
rc
88
89.
Приток к скважине, расположенной вблизинепроницаемой прямолинейной границы
Данная
задача
может
возникнуть
при
расположении добывающей скважины вблизи
сброса или около границы выклинивания
продуктивного пласта
МЕТОД - отображения источника и стока
Исходные формулы
(n=2)
n
1
сi
G i ln rci G j ln rji C
2 h
j 1, i j
1 n
к
G j ln rк C
2 h j 1
2 h н с
G
rк2
ln
rc 2а
89
90.
Приток к скважине в пластес произвольным контуром питания
. Схема видов
контуров питания
1. При вычислении дебита скважины форма
внешнего контура пласта не имеет скольконибудь существенного значения.
2. Чем дальше от внешнего контура пласта
находится скважина, тем меньший дебит она
имеет. Однако, так как величина расстояния
входит под знаком логарифма, то даже
значительное изменение этого расстояния
мало влияет на величину дебита
3. В случае расположения скважины
эксцентрично относительно контура поток
можно считать плоско-радиальным и дебит
рассчитывать по формуле Дюпюи если
rк.>103 rc и эксцентриситет а1< rк /2.
90
91.
Приток к бесконечным цепочкам и кольцевымбатареям скважин
Приток к скважинам кольцевой батареи
Исходные формулы
n
1
сi
G i ln rci G j ln rji C
2 h
j 1, i j
1 n
к
G j ln rк C
2 h j 1
Граничные условия:
на контуре питания = к=const при rj=rк;
на контуре скважины = с=const при r1=rс;
rj(j 1)=2a sin[(n-1) /n].
91
92.
При данных гр. условиях:G
к
ln rкn C
2 h
n 1
G
j
n 1
с
ln 2a rc sin C
2 h
n
j 1
G
с
ln na n 1rc C
2 h
2 h к с
Выражение для дебита одной
G
скважины
rкn
ln n 1
na rc
Т.к.
j
n
sin n 1 , то
n 2
j 1
n 1
Область применения: размеры пласта во много раз больше
площади внутри окружности батареи скважин (rк 10а ) случай водонапорного режима.
2 h к с
G
rк2n a 2n
ln n 1 n
na rcrк
- rк 10а - случай режима растворенного
газа
92
93.
Дебит батареиG бат
2 h к с
к с
n
2 a
rк n a
ln
1
rк
1
n
ln
ln
а
nr
c
2 h а 2 hn 2 rc
Поле течения в области действия круговой батареи
Уравнение линий изобар
2 j 1
a
r
2
ar
cos
C1
j 1
n
n
2
2
Нейтральные линии тока Н сходятся в центре батареи и делят
расстояние
между
двумя
соседними скважинами пополам.
Главные линии тока Г - проходят
через центры скважин и делят
сектор,
ограниченный
двумя
нейтральными линиями, пополам.93
94.
Скорость фильтрации по главным линиям максимальна, а понейтральным линиям - минимальна. В центре кольцевой батареи
скорость фильтрации равна нулю, т.е. частица жидкости,
находящаяся в точке, в которой изобара пересекает сама себя,
неподвижна. Такие точки фильтрационного поля называются точками
равновесия и при разработке в окрестностях таких точек образуются
“застойные области”.
Семейство изобар подразделяется на два подсемейства, которые
разграничиваются изобарой пересекающей себя в центре батареи
столько раз, сколько скважин составляет данную батарею. Первое
подсемейство изобар определяет приток к отдельным скважинам и
представляет собой замкнутые, каплеобразные кривые, описанные
вокруг каждой скважины. Второе семейство - определяет приток к
батарее в целом и представляет собой замкнутые кривые, описанные
вокруг батареи.
94
95.
Оценки эффекта взаимодействия скважин круговойбатареи:
дебит изменяется непропорционально числу скважин и
радиусу батареи (расстоянию между скважинами);
с увеличением числа скважин дебит каждой скважины
уменьшается при постоянном забойном давлении, т.е.
растет эффект взаимодействия;
взаимодействие скважин может практически не
проявляться только при очень больших расстояниях
между скважинами (в случае несжимаемой жидкости,
строго говоря, влияние скважин распространяется на весь
пласт);
с увеличением числа скважин темп роста суммарного
дебита батареи замедляется т.е. сверх определённого
предела
увеличение
числа
скважин
оказывается
неэффективным в виду прекращения прироста дебита.
95
96.
Приток к прямолинейной батарее скважинРежим: удаленный контур питания и постоянные забойные давления
Состав по числу скважин : четный и нечетный
Эффекты взаимодействия
Величина дебитов скважин:равноудаленные от середины
или от концов батареи - одинаковы, а при разной
удаленности - отличаются.
Для однородных пластов и жидкостей относительные
изменения дебитов скважин, вызванные эффектом
взаимодействия, не зависят от физико-геологических
характеристик пласта и от физических параметров
жидкости.
96
97.
Формула Голосова П.П. для общего дебита скважинпрямолинейной батареи:
G бат
G бат
2 h 2n 1 к c
2
n
L
L
ln ln
rc j 1 j 2
4 hn к c
n
L2
L2
ln
ln
rc j 2 j j 1 2
- для нечетного числа
скважин 2n+1, где n - любое
целое число
- для четного числа скважин
Здесь h - толщина пласта; - расстояние между скважинами; L –
расстояние до контура.
Ошибка в определении дебитов по данным формулам не
превышает 3-4% при L=10км, rс=10см, при расстояниях между
скважинами 100м 500м.
97
98.
Фильтрационное поле бесконечной цепочкиравностоящих скважин
Формула дебита - из формулы дебита скважин круговой
батареи при rк = L + a; a = n /(2 ), где L = const разность между радиусом контура питания и радиусом
кольцевой батареи а; = const - длина дуги окружности
радиусом а между двумя соседними скважинами кольцевой
батареи.
2 h к с
G
rкn
ln n 1
na rc
Подставим значения rк , a
98
99.
G2 h к с
n
2 l
ln 1
ln
n
2 rс
Где z= / (2 L),
2 h к с
1
z
nz
1
ln 1 ln
zn
2 rс
nz
1
lim 1 =е
hz
nz
Массовый дебит скважин линейной батареи
2 h к с
G
2 L
ln
2 rс
Здесь L - расстояние от контура питания до батареи; расстояние между скважинами батареи; h - толщина
пласта.
99
100.
Массовый дебит батареи из n скважинG
к с
L
1
ln
nh 2 hn 2 rс
Для несжимаемой жидкости
Q
pк pс
L
ln
knh 2 khn 2 rс
100
101.
Главные Г и нейтральные Н линии тока перпендикулярны цепочке.• Нейтральными линиями тока вся плоскость течения делится на
бесконечное число полос, каждая из которых является полосой
влияния одной из скважин, находящейся в середине расстояния
между двумя соседними нейтральными линиями.
• Изобара, бесчисленное множество раз пересекающая сама себя,
отделяет изобары внешнего течения ко всей батареи,
охватывающих всю цепочку скважин, от изобар притока к скважине,
охватывающих только данную скважину.
•Точки пересечения граничной изобары являются точками
равновесия.
101
102.
Метод эквивалентных фильтрационныхсопротивлений (метод Борисова)
Метод позволяет сложный фильтрационный поток в
пласте при совместной работе нескольких батарей
эксплуатационных и нагнетательных скважин разложить
на простейшие потоки - к одиночно работающей
скважине и к одиночно работающей батареи.
закон Ома
I =U / R
Дебит прямолин. батареи
G
к с
L
1
ln
nh 2 hn 2 rс
сопротивления
внешнее
внутреннее
102
103.
Внешнее фильтрационное сопротивление - выражаетфильтрационное сопротивление потоку от контура питания к
участку прямолинейной бесконечной цепочки, занятому n
скважинами, в предположении замены батареи галереей.
L
L
или р
nh
nkh
Дебит равен дебиту в прямолинейно-параллельном потоке
через площадь величиной n h на длине L .
Внутреннее
сопротивление
выражает
местное
фильтрационное сопротивление, возникающее при подходе
жидкости к скважинам за счет искривлений линий тока
1
ln
или р
ln
2 nh 2 rc
2 nkh 2 rc
Дебит равен
суммарному дебиту n скважин при
плоскорадиальном течении, в предположении, что каждая
скважина окружена контуром питания длиной (аналог
формулы Дюпюи)
103
104.
Сопротивлениякольцевой батарея
Внешнее
1
rк
ln
2 h a
Внутреннее
2 a
1
ln n
2 hn 2 rc
области
внутреннего
сопротивления
затемнены.
Схема одной батареи
Электрическая схема
одной батареи
104
-
105.
«n» нагнетательных и эксплуатационныхбатарей
a)
b)
Схема n-батарей с двумя контурами питания
а) линейные батареи; b) кольцевые батареи
105
106.
Электрическая схема n-батарей с двумя контурами питанияСопротивления
прямолинейная батарея
Li
i
;
k i h i
1
i
i
ln
2 h 2 rci
круговая батарея
1
ri 1
1
i
i
ln ; i
ln
2 h ri
2 h 2 rci
106
107.
Законы Кирхгоффаn
1.
Gi 0
i 1
2.
G i i G i i i
для последовательных сопротивлений = i , а
1
для параллельных - 1
i
.
Приведенные формулы тем точнее, чем больше расстояние
между батареями по сравнению с половиной расстояния
между скважинами
Схема замены
соседних батарей
скважин одной
батареей
107
108.
Приток к несовершенным скважинамВиды несовершенств
По степени вскрытия
По характеру вскрытия
a)
b)
Схема притока к несовершенной скважине
а - по степени вскрытия; b - по характеру вскрытия
108
109.
Параметр несовершенстваG
Gс
Параметр несовершенства зависит от
h вс
h
h
• относительного вскрытия пласта
• плотности перфорации (числа отверстий, приходящихся
на 1м фильтра), размеров и формы отверстий;
глубины прострела.
Приведенный радиус несовершенной скважины
rпр rce C
Приведенный радиус - это радиус такой совершенной скважины,
дебит которой равняется дебиту данной несовершенной скважины
при тех же условиях эксплуатации
109
110.
Влияние несовершенства скважины на приток присуществовании закона фильтрации Дарси можно учесть
основываясь на электрической аналогии.
Согласно
данной
аналогии
различие
в
дебитах
совершенной Gc и несовершенной G скважин объясняется
наличием добавочного фильтрационного сопротивления
несовершенной скважины величиной С/2 h, т.е. дебит
несовершенной скважины можно представить в виде:
к с
G
.
1
rк
(ln С)
2 h
rс
Отсюда
rк
rк
ln
ln
rс
rс
rк
rк
ln С ln
rс
rпр
110
111.
Экспериментальные и теоретические исследованияпритока жидкости к гидродинамически
несовершенной скважине
Течение по закону Дарси
Несовершенство по характеру вскрытия: В.И. Щуров
С = С ( a, h) (a=h/D, h - мощность пласта, D- диаметр
скважины; h=hвс/h, hвс - толщина вскрытия ) .
Несовершенство по степени вскрытия: И.М. Доуэлл, Маскет,
Р.А. Ховард и М.С. Ватсон
С = С (плотности перфорации, глубины прострела)
Плотность перфорации - число отверстий на 1 метр
Дебит значительно зависит от плотности перфорации только
до значений 16-20 отверстий на 1 метр
111
112.
Формула Маскета для дебита несовершенной по степенивскрытия скважины (основа метод суперпозиции и
отображения стоков)
2 h к с
G
1
4h
4h
2 ln
f h ln
2h
rc
rк
f - функция относительного
вскрытия
Коэффициент несовершенства
1
4h 1
С 1 ln
f (h )
h
rc 2h
Формула Н.К.Гиринского применяется если толщина
пласта много больше радиуса
скважины
2 h к с
G
1.6h
ln
rк
112
113.
Если скважины несовершенны по характеру вскрытия,то коэффициент С увеличивается на величину
сопротивления фильтра
120
C
Dn h
D - диаметр фильтрового отверстия в см; n - число
отверстий на 1м перфорированной части.
113
114.
Приток реального газа по двухчленномузакону к несовершенной скважине
Уравнение притока реального газа по двухчленному закону
фильтрации к совершенной скважине
2
к
2
с
~ ~z p
~z p
R
cт
cт
А
ln к ; B = cт
kh
rc
2 2h 2rc k
2
cт
р р АQ cт BQ
Уравнение притока реального газа по закону Дарси к
совершенной скважине
2
к
2
2
р р AQcт
Приток к несовершенной скважине учитывается, введением приведённого радиуса скважины в формулу дебита
rc rce
( C C )
114
115.
1) R1 (2-3) rc -из-за
больших скоростей вблизи
перфорации
происходит
нарушение закона Дарси и
проявляется
в
основном
несовершенство по характеру
вскрытия; закон фильтрации двухчленный ;
2
р 22 р12 А1Qcт B1Qcт
~ ~z p
R
cт
А1
(ln 1 C 3 );
kh
rc
cт ~z p cт 1
1
B1 = 2 2
C4
2 h k rc R 1
С3 - по графикам Щурова, а С4 по формуле
h2
С4
3N 2 R 02
N- суммарное число отверстий; R0- глубина проникновения
перфорационной пули в пласт.
115
116.
2) R2 h - линии тока искривляются из-за несовершенства постепени вскрытия; фильтрация плоскорадиальна, но с переменной
толщиной (от hвск до h); закон фильтрации - двухчленный .
2
2
2
1
р р А1Qcт B1Q
2
cт
~ ~z p
~z p 1
R
1
cт
cт
cт
2
А1
(ln
C1 ); B1 = 2 2
C2 ;
kh
R1
2 h k R 1 R 2
1
1 h
h
C1 ln h
ln ;
h
h
R1
h вс
1
1
C2 2 1 ; h =
.
h
h
h
3) R2< r< Rк - действует закон Дарси и течение плоскорадиально
2
к
2
2
р р AQcт
116
117.
Общее уравнение притока к несовершеннойскважине
2
к
2
с
р р АнQcт ВнQ
2
cт
~ ~z p
~z p
R
cт
cт
1 rcC2 rC 4 .
Ан
(ln 2 C1 С3 ); Bн = cт
2 2
kh
R1
2 h rc k
117
118.
Интерференциянесовершенных скважин
1) Определяется дебит совершенных скважин с
радиусами rс по формулам теории интерференции для
притока к стокам и источникам на плоскости.
2) Фильтрационное сопротивление каждой скважины
увеличивается на величину коэффициентов
несовершенства Сi (i = 1,...,4).
3) Используется метод эквивалентных фильтрационных
сопротивлений для исследования интерференции
несовершенных скважин, в том числе при двухчленном
законе фильтрации в виде
р АQ Q
BQ (Q) - нелинейное сопротивление, добавляемое
к внутреннему сопротивлению .
118
119.
Взаимодействие скважин в неоднороднопроницаемом и анизотропном пластах
А) Кольцевая батарея во
внутренней области
Исходные соотношения для дебитов:
1 -ая зона -
2-ая зона -
Исключим 0
G G 1 G 2
2 h 0 с
G
R n0
= kФ+С, где
ln n 1
na rc
2 h к 0
G
Rк
n ln
R0
Ф dp
2 h Фк Фс
R
1
1 Rк
ln
ln
k 1 na rc k 2 R 0
n
0
n 1
n
119
120.
Анализ формулы:1) При k1/k2 = < 1 величина коэффициента суммарного взаимодействия
(отношение суммарного дебита группы совместно
Gi
U
G действующих скважин к дебиту одиночной скважины)
всегда выше, чем U батареи, действующей при тех же
условиях в однородном пласте ( = 1).
2) Если же >1, то U будет меньше его значения в однородном
пласте.
Б) Кольцевая батарея во внешней области (а > R0).
2 h Ф к Ф с
G
R nк
k 2 k1
a 2n
ln n 1
ln 2n
na rc k 2 k 1 a R 02n
120
121.
Анизотропный пластЭффект взаимодействия будет значительно усиленным или
ослабленным лишь при резком различии проницаемостей в двух
определённых направлениях: в направлении линии расстановки
скважин и в направлении перпендикулярном к этой линии.
Ослабление взаимодействия наблюдается в случае более
низкой проницаемости в направлении линии расстановки скважин
по
сравнению
с
проницаемостью
в
перпендикулярном
направлении. Усиление эффекта взаимодействия происходит в
обратном случае. Таким образом, для уменьшения эффекта
взаимодействия при закладывании новых скважин следует
выбирать направление, в котором пласт наименее проницаем.
121
122.
Влияние радиуса скважины на её производительностьОдиночная скважина
rс - радиус 1 -ой скважины, rc/=xrc - радиус 2 -ой скважины;
G - дебит 1 -ой скважины, G/ =уG - дебит 2 -ой скважины;
Закон
фильтрации
Дарси
Краснопольского
плоскорадиальный
R
ln к
rc
y
R
ln к ln x
rc
у х
Тип потока
радиально-сферический
у=х
у х3
122
123.
Взаимодействие скважинСравнение дебитов скважин кольцевой батареи из n
эксплуатационных скважин в двух случаях: 1)скважины
имеют радиус rc и 2)скважины имеют радиус хrc.
R nк
ln n 1 ln x
na rc
Gx
у
G1
R nк
ln n 1
na rc
В центре батареи действует нагнетательная скважина с
дебитом равным дебиту батареи
n 1
a
ln n
ln
xrc
у
n 1
a
ln ln n
rc
123
124.
Анализ1) с увеличением числа эксплуатационных скважин кольцевой
батареи влияние их радиуса на дебит уменьшается, если
отсутствует нагнетание жидкости в пласт;
2) если в центре батареи находится нагнетательная скважина,
то влияние радиуса скважины на дебит будет больше, чем при
отсутствии центрального нагнетания жидкости в пласт.
При этом радиус скважины влияет на производительность
больше, чем при одиночной эксплуатационной скважине. Число
скважин мало влияет на производительность.
Таким образом, взаимодействие эксплуатационных скважин с
нагнетательными повышает влияние радиуса скважин на дебит.
124
125.
НЕСТАЦИОНАРНАЯ ФИЛЬТРАЦИЯУПРУГОЙ ЖИДКОСТИ
Упругий режим - основная форма пластовой энергии энергия упругой деформации жидкостей и материала
пласта.
Упруговодонапорный - приток жидкости поддерживается
за счет напора воды, поступающей извне.
Замкнуто-упругий залежи нефти ограничены либо
зонами выклинивания, либо экранами.
Жестко-водонапорный режим - вытеснение жидкости из
пласта происходит не под действием преобладающего
влияния упругости пласта и жидкости (упругие свойства
проявляются мало)
125
126.
Особенности упругого режима:процессы перераспределения давления в пласте неустановившиеся ;
упругий запас жидкости в пласте изменяется.
Неустановившиеся процессы протекают тем быстрее, чем больше
коэффициент проницаемости пласта k, и тем медленнее, чем больше
вязкость жидкости и коэффициенты объёмной упругости жидкости и
пласта.
Параметры упругого режима
Важнейшие параметры упругого режима: коэффициенты
объёмной упругости жидкости и пласта.
Коэффициент
объёмной
упругости
жидкости
ж
характеризует податливость жидкости изменению её объёма и
показывает, на какую часть первоначального объёма изменяется
объём жидкости при изменении давления на единицу.
1 d ж 1 d
ж
ж dp dp
ж нефти - (7-30)10-10м2/н;
ж воды - (2,7-5)10-10м2/н.
ж - объём жидкости; знак минус
указывает на то, что объём ж
увеличивается
с
уменьшением
давления;
126
127.
Коэффициент объёмной упругости пласта1 d п dm
c
п dp dp
Упругий
запас
п - объём пласта; m - пористость; С слабо и
сильно сцементированных горных
находится в пределах (0,3-2)10-10м2/н.
пород
з
это
количество
жидкости,
высвобождающейся в процессе отбора из некоторой области пласта
при снижении пластового давления до заданной величины, если
высвобождение происходит за счет объёмного расширения жидкости
и уменьшения порового пространства пласта.
з = ж 0ж р + с 0 р= * 0 р. ,
где 0ж - объём жидкости, насыщающей элемент объёма пласта 0
при начальном давлении р0; р - изменение давления;
* = m ж + с - коэффициент упругоёмкости пласта, показывающий
долю объема жидкости от выделенного элемента объема пласта,
высвобождающейся из элемента пласта при снижении давления на
единицу
127
128.
Коэффициент пьезопроводности пласта - характеризуетскорость распространения изменения пластового давления
k
= * L2T 1
В коллекторах – 1000см2/с 50000см2/c или
0.1м2/с 5м2/c.
Параметр Фурье - определяет степень нестационарности процесса
κt
fo 2
rc
κt
Fo 2
rк
128
129.
Дифференциальное уравнение неустановившейсяфильтрации упругой жидкости
(уравнение пьезопроводности)
Допущения: 1) течение по закону Дарси; 2) зависимость плотности
и пористости от давления линейны
0 1 ж р р 0
m
* p
0
t
t
p
р
t
m m 0 1 c р р 0
1 d п dm
c
п dp dp
k
m
dp C
t
- уравнение пьезопроводности,
позволяет определить поле давления
при нестационарных процессах в
пласте с упругим режимом.
129
130.
Приток к скважине в пласте неограниченныхразмеров
Вывод основного уравнения упругого режима
Пласт упругий, горизонтальный и большой
протяженности и в нём имеется одна скважина, тогда
движение
жидкости
в
пласте
можно
считать
плоскорадиальным.
Уравнение пьезопроводности в цилиндрических
координатах
2 р
r 2
1 р 1 р
r t
r
возмущение вызвано
мгновенным стоком,
существовавшим в момент t = t/
Решение
r2
С = рк. - при t = t/ /правило Лопиталя/
A
p( r , t ) C
e
t t
4 (t- t )
2
A
- из d з = * рd 0 130
4 hk
131.
Изменение давления во времени для скважины,введенной в неограниченный пласт в некоторый
(начальный) момент времени и действующей мгновенно
2
p( r , t ) р к
e
4 hk (t t )
r2
4 (t- t )
Изменение давления во времени для скважины,
действовающей непрерывно с постоянным дебитом Q =
Q0 в течение времени dt/
r2
4κ(t- t )
0
Q
p( r , t ) р к
e
4 hk 0
dt
t t
131
132.
Интегрально-показательная функцияr 2 e u
Ei
du
4 t r 2 u
4 сt
Основная формула упругого режима
Q 0
p( r , t ) р к
4 hk
r 2
Ei
4κt
Свойства интегрально-показательной функции:
-Ei(-u) изменяется от 0 до
при изменении аргумента от 0 до ;
функция -Ei(-u) представляется
в виде сходящегося ряда
1
u2 u3
Ei ( u) ln 0,5772 u
.....
u
4 18
Для малых u
1
Ei ( u ) ln 0,5772
u
132
133.
Q0 4 tКривая КВД: p(r, t ) рк
ln
0
,
5772
(1)
2
4 hk r
κt
fo 2 100
rc
погрешность не превышает 0,6% для бесконечного
пласта.
для
конечного пласта погрешность расчета
давления не превышает 1%, если rк > 1000rc и fo <
3,5.105 или Fo < 0,35.
Из (1)
Пьезометрические кривые при
пуске скважины в бесконечном
пласте с постоянным дебитом
p Q 0 1
r 2 kh r
Выводы:пьезометрические
кривые
представляют
собой
логарифмические линии.
Углы наклона касательных на
забое скважины одинаковы для всех
кривых.
133
134.
Анализ основной формулы теории упругого режима1. Основная формула строго справедлива лишь для точечного
стока, т.е. при rс=0. Практические расчеты показывают, что ей
можно пользоваться даже для укрупнённых скважин (rс 1км) и
нельзя использовать только в первые доли секунды после пуска
скважины.
2. Вскоре после пуска скважины вокруг неё начинает непрерывно
увеличиваться область пласта, в которой для каждого момента
времени давление распределяется так, как и при установившемся
движении, т.е. давление оказывается квазиустановившимся и
пьезометрические кривые будут кривыми логарифмического типа.
p Q0 1
e
r 2 hk r
r2
4 t
Q0 1
; u=
e
2 h r
r2
4 t
.
Стационарная скорость достигается очень быстро на небольших
расстояниях от скважины.
134
135.
Приток к скважине в пласте конечных размеров вусловиях
упруго-водонапорного и замкнутоупругого режима
Приток к скважине в пласте конечных размеров с
открытой внешней границей
Исходные уравнения
Уравнение упругого режима
Q 0
p( r , t ) р к
4 hk
r 2
Ei
4κt
Формула Дюпюи
Q 0
p( r , t ) р к
4 hk
r 2
Ei
4κt
Решаем совместно
135
136.
Уравнение для давления2
r 1
рк р
р
1
Ei
rк rк 4Fo
рк р у р у
2 ln
r
ру - установившееся давление в любой точке пласта или в
реагирующей бездействующей скважине (t = или Fo = ).
Пьезометрические кривые при пуске скважины в конечном
пласте с открытой внешней границей
а - с постоянным дебитом;
b - с постоянным забойным давлением рс
Изменение
дебита
скважины с
течением
времени при
постоянном
забойном
давлении
136 рс
137.
Круглый горизонтальный пласт с закрытойвнешней границей
Пьезометрические кривые
при пуске скважины в
конечном
пласте
с
закрытой
внешней
границей при постоянном
дебите
Пьезометрические
кривые
при
пуске
скважины в конечном
пласте с закрытой
внешней границей при
постоянном забойном
давлении
Изменение дебита
Q (кр.1) скважины и
суммарной добычи
Qcp (кр.2) с течением времени t
137
138.
Взаимодействие скважин принеустановившихся процессах
По методу суперпозиции
2
r
j
р p j
Q j Ei
4 hk j 1
4
t
j 1
n
n
n - число скважин; Qj - объемный дебит стока (+) или источника(-) за
номером j; р -понижение давления в какой либо точке пласта; rjрасстояние данной точки пласта от скважины за номером j
n
2,246κt
р p j
Q j ln
2
4
hk
r
j 1
j 1
j
n
Данная зависимость используется для расчета параметров
пласта путем обработки кривой восстановления давления в
случае
скважины,
эксплуатирующейся
в
течение
длительного времени и остановленной для исследования.
138
139.
Периодически работающая скважинаПостановка
задачи. В
неограниченном пласте
останавливается
скважина,
эксплуатирующаяся
с
постоянным дебитом Q в течении времени Т, сравнимого
со временем проведения исследований.
С момента остановки давление в скважине и окружающей
области пласта повышается, т.е. с данного момента
можно считать, что одном и том же месте пласта
действуют совместно и непрерывно эксплуатационная
(сток) и нагнетательная (источник) скважины. При этом
источник имеет тот же дебит Q. Обозначим повышение
давления за счет работы источника через р//.
139
140.
Q 4 (Т t )p
ln
0
,
5772
2
4 hk
r
Q 4 t
p
ln 2 0,5772
4 hk r
Результирующее понижение давления
Q
Т t
p p p
ln
4 hk
t
или
Q
t
p с p к 0,1832
ln
hk Т t
Зависимость
(1)
используется
при
гидродинамических
исследованиях
скважин, работающих не
продолжительное
время, методом построения
кривой восстановления
давления.
(1)
140
141.
Определение коллекторских свойствпласта по данным исследования скважин
нестационарными методами
Уравнение КВД
р с р к р с A i ln t ,
Q 0
2,246
где А=i ln
; i=
.
2
4 hk
rс
141
142.
Неустановившееся фильтрация газа впористой среде
Уравнение Лейбензона
Исходные соотношения
kp
P
ΔP
mμ
t
р2=Р
ст
р
рст
k ст 2
р С
2 рст
Р=р2, -- /=
kp к ,
mμ
Q Q р
ст ст
2 kh
kh
142
143.
2Q
р
r
2
ст ст
p( r , t ) р к
Ei
2 hk
4 t
Qстрст 2,25 t
p(r, t ) р
ln
2 hk
r2
2
к
(1)
Пьезометрические
кривые
при
неустановившемся притоке газа к
скважине в разные моменты времени
(а) и изменение давления с течением
времени в фиксированных
пласта (b)
точках
Уравнение (1) используется для расчета коллекторских параметров
газовых пластов методом обработки КВД. Принцип расчета такой же,
что и в случае нефтяных скважин, но для получения линейной
зависимости по оси ординат надо откладывать не депрессию, а
разность квадратов пластового и забойного давлений
143
144.
ОСНОВЫ ТЕОРИИ ФИЛЬТРАЦИИМНОГОФАЗНЫХ СИСТЕМ
Связь с проблемой нефтегазоотдачи пластов
Углеводородные
системы
Гомогенные
Составляющие (компоненты)
“размазаны” по пространству
и взаимодействуют на молекулярном уровне. Изменение
физических и химических
свойств непрерывно.
Гетерогенные
Составляющие(фазы) - разделены
отчетливыми
геометрическими
границами и взаимодействуют на
поверхностях раздела. Изменение
физических и химических свойств
разрывно.
144
145.
Характеристикимногофазной среды
Насыщенность
Насыщенностью i порового
пространства i –й фазой
называется доля объема пор
Vi , занятая этой фазой в
элементарном объеме:
Vi
i
Vп
n
i 1
i 1
Скорость фазы
вектор скорости фильтрации ui
фазы
определяется
как
вектор, проекция которого на
некоторое
направление
L
равна отношению объемного
расхода Qi данной фазы к
площадке i , перпендикулярной
к
указанному
направлению:
Qi
ui L
i
145
146.
Допущение:• каждая фаза двигается под действием своего давления
Закон фильтрации каждой из фаз:
k
u i k i ( ) gradp i i g
i
Характерная несимметричная форма
кривых относительной проницаемости
объясняется тем, что при одной и той
же насыщенности более смачивающая
фаза
занимает
преимущественно
мелкие
поры
и
относительная
проницаемость у неё меньше.
Сумма относительных проницаемостей для
каждого
фиксированного
значения
меньше 1.
Зависимость относительных
проницаемостей ki от насыщенности
k 1 ( ) k 2 ( ) 1
Присутствие связанной смачивающей фазы мало влияет на течение не
смачивающей жидкости, тогда как присутствие остаточной не смачивающей
фазы значительно "стесняет" движение смачивающей фазы.
146
147.
Диаграмма для определенияграниц преобладания потоков
различных фаз при трехфазном течении
Характер
зависимостей
определяется
различной
степенью
смачивания твердых зерен породы
фазами, причем оказывается, что
относительная
проницаемость
зависит
только
от
водонасыщенности - наиболее проницаемой
фазы - воды, и почти не зависит от
нефте- и газонасыщенности.
Относительная
фазовая
проницаемость в многофазном
потоке почти не зависит от вязкости
жидкости,
ее
плотности,
внутрижидкостного
натяжения,
градиента давления.
147
148.
Капиллярное давление - рк =р2-р1Большее давление - на стороне жидкости, не смачивающей
твердые зерна породы.
m
р к р к ( ) п cos
J( )
k
п - коэффициент межфазного поверхностного
натяжения; - статический краевой угол
смачивания между жидкостями и породой; m пористость; J( ) — безразмерная функция
Леверетта.
Зависимость
функции
Леверетта от насыщенности:
1 - кривая вытеснения; 2 - кривая
пропитки;
А
остаточная
насыщенность
вытесняемой
жидкости
148
149.
Процессы многофазной фильтрации зависят от:1) от характерного времени фильтрационного процесса;
2) размеров области течения
Влияние капиллярных сил на распределение давления
незначительно и их действие проявляется в локальных процессах
перераспределения фаз.
Исходные уравнения многофазной фильтрации
Уравнения неразрывности
m 1 div 1u 1 0
t
m 2 1 div 2 u 2 0
t
Жидкости несжимаемы - нестационарные процессы упругого
перераспределения давления заканчиваются в начале
процесса вытеснения
m
div u 1 0
t
m
div u 2 0
t
149
150.
Уравнения движения для многофазной фильтрацииk
u i k i ( ) gradp i i g
i
Связь между давлениями
m
р 2 р 1 р к ( ) п cos
J( )
k
150
151.
Одномерные модели вытеснения несмешивающихсяжидкостей
Основные допущения:
жидкости предполагаются несмешивающимися (взаимно
нерастворимыми);
жидкости считаются несжимаемыми, а пористая среда недеформируемой; фазовые переходы отсутствуют;
коэффициенты вязкости фаз постоянны;
относительные фазовые проницаемости и капиллярное
давление являются известными однозначными функциями
насыщенности;
гистерезисные явления не учитываются (рассматриваются только
однонаправленные процессы).
151
152.
Полная система уравненийm
u 1
t
х
u 2
m
t
х
k
p 1
u 1 k 1 ( )
1 g sin
1
x
u2
k
p
k 2 ( ) 2 2 g sin
2
x
Характерной особенностью данной системы является то, что её можно
свести к одному уравнению для насыщенности.
Знание распределения насыщенности в пласте позволяет
проанализировать эффективность вытеснения нефти или газа
несмешивающейся с ними жидкостью.
Данное уравнение представляет собой сложное нелинейное
уравнение параболического типа второго порядка и точное решение
получено лишь для некоторых сравнительно простых частных случаев.
152
153.
Модель Рапопорта Лиса - для прямолинейнопараллельного вытеснения уравнение для насыщенностибез учета силы тяжести.
Дифференциальное уравнение для насыщенности в данной модели –
параболического типа.
Модель Баклея Леверетта - без учета капиллярных
сил.
Уравнение насыщенности задач данного типа принадлежит к классу
квазилинейных гиперболических уравнений первого порядка.
153
154.
Задача Баклея Леверетта и ее обобщенияФункция Баклея Леверетта или
функция распределения потоков фаз f( ) представляет собой отношение скорости фильтрации
вытесняющей фазы к суммарной скорости, и равна
объемной доле потока вытесняющей жидкости (воды) в
суммарном потоке двух фаз.
Функция Баклея Лаверетта определяет
полноту вытеснения и характер распределения
газоконденсатонефтенасыщенности по пласту.
Вид функции
Баклея-Леверетта и
её производной
Задачи повышения нефте- и газоконденсатоотдачи в значительной
степени сводятся к применению таких воздействий на пласт, которые
в конечном счете изменяют вид функции f( ) в направлении
увеличения полноты вытеснения
154
155.
Графики функции Баклея - Леверетта (а) и еёпроизводной (b) для различных отношений
вязкости 0= 1 / 2
Дисперсия волн -
С ростом отношения вязкостей
кривая f( ) сдвигается вправо и
эффективность
вытеснения
возрастает.
зависимость скорости распространения
того или иного
значения насыщенности от величины этой насыщенности.
При 0 п большие насыщенности
распространяются
с
большими
скоростями, а при п 1 скорость
распространения
постоянного
значения насыщенности начинает
уменьшаться.
Устранение
многозначности
распределения насыщен-ности
введением скачка
155
156.
Задача Рапопорта – ЛисаРаспределение насыщенности
в стабилизированной зоне l
Cтабилизированная зона насыщенности перемещается, не
изменяя своей формы, и распределение насыщенности в
ней при постоянной скорости вытеснения – стационарно.
156
157.
Рассматриваемнелинейные
законы
фильтрации,
описывающие
только
безинерционные движения при условии, что
фильтрующиеся
жидкости
обладают
неньютоновскими свойствами.
157
158.
Реологические модели фильтрующихсяжидкостей
du
dy
Ньютоновские
жидкости
du
f
dy
du
f , t
dy
Стационарно
реологические
жидкости
Нестационарно
реологические
жидкости
du d
f ,
dy dt
Вязкоупругие
жидкости
Вязкоупругие жидкости - среды, обладающие свойствами
как твердого тела, так и жидкости, а также способные к
частичному восстановлению формы после снятия
158
напряжений.
159.
Стационарно реологическиежидкости
du 1
0 при > 0,
dy
du
0
dy
при 0.
Вязкопластичные
жидкости
0- начальное
(предельное) напряжение
сдвига
*
du
dy
a) n < 1
du
k
dy
Псевдопластичные
жидкости
n
b) n > 1
Дилатантные
жидкости
Связь между и градиентом скорости в
логарифмических координатах на некотором участке линейна с угловым коэффициентом (от 0 до 1- a, . от 1 до 2 - b)
- кажущаяся
*
вязкость
du
* k
dy
убывает с
возрастанием
градиента скорости.
n 1
* увеличивается с
возрастанием
градиента скорости.
159
160.
Зависимость касательного напряженияот градиента скорости
жидкость: 1 - дилатантная; 2 - ньютоновская; 3 псевдопластичная; 4 - вязкопластичная
Дилатантная -суспензии с
большим содержанием твердой фазы.
Псевдопластичная - растворы
и расплавыполимеров
160
161.
ЗАКОНЫ ФИЛЬТРАЦИИВязкопластичная жидкость в пористой среде
u
gradp u
k
u
gradp ,
- u>0;
u=0, где
~
0
k
предельный
(начальный)
градиент
Индикаторные линии:
1 - линейная аппроксимация неньютоновской жидкости; 2 - реальная неньютоновская
жидкость; 3 - течение по закону Дарси
Неньютоновские эффекты проявляются
при малых скоростях фильтрации и в
средах с малым размером пор, т. е. с
малой проницаемостью
161
162.
Из-за неньютоновских свойств нефтей пропласткипоследовательно
включаются в работу по мере
превышения градиента давления предельного
градиента сдвига.
Степенной закон фильтрации
n
u C gradp gradp , где С — экспериментальная
константа; n>0.
Степенной закон, соответствующий псевдопластичному флюиду, хорошо описывает движение
растворов полимеров в пористой среде и
используется
при
расчете
“полимерного”
заводнения пластов с целью повышения их
162
нефтеотдачи.
163.
Одномерные задачи фильтрациивязкопластичной жидкости
Установившееся течение вязкопластичной жидкости
dp
u
k
Поток плоскорадиален и dr
dp
dr
Отсюда формула притока u
(u>0);
(u=0).
Q
k dp
, если dp
2 rh dr
dr
u=0,если dp/dr
163
164.
Интегрируем формулу притока при р(rc)=рc; р(Rк)=ркQ
r
p(r ) pc r rc
ln ,
2 kh rc
rc r R к
2 kh
p c R к при p c R к ;
R
ln к
rc
Q 0 при p c R к p c р к р с .
Q
Анализ
• Часть разности давлений в виде линейного слагаемого с угловым
коэффициентом теряется на преодоление предельного градиента
сдвига.
• При Q 0давление не постоянно (как в случае фильтрации по
закону Дарси), а изменяется по линейному закону.
• При тех же условиях наличие предельного градиента давления в
пласте ведет к уменьшению дебита скважины по сравнению с
фильтрацией по закону Дарси (формула Дюпюи).
• Индикаторная линия скважины Q( рс) - прямолинейная, но не
проходит через начало координат, а отсекает на оси депрессий
164
отрезок, равный Rк.
165.
Слоистый пластИндикаторные линии при
плоскорадиальном течении
вязкопластичной жидкости через
трёхслойный пласт.
Неустановившаяся фильтрация
вязкопластичной жидкости
Уравнение пьезопроводности:
p
gradp ,
div 1
t
gradp
gradp
При решении нестационарных задач на основе модели
фильтрации с предельным градиентом в пласте образуется
переменная область фильтрации, на границе которой (пока она не
достигнет границы пласта) модуль градиента давления должен
равняться предельному градиенту а давление - начальному
пластовому.
165
166.
Пуск скважины с постоянным дебитом при фильтрациивязкопластичной жидкости с предельным градиентом
Из решения уравнения пьезопроводности
получаем зависимость забойного давления
от времени
Q
Q t
3Q t
pc pк
ln
3
6 kh kh rc
kh
Основная роль при малом
времени, когда преобладают
упругие силы.
1
3
Q
2 kh
При больших значениях
времени
166
167.
Образование застойных зон при вытеснениинефти водой - эффект фильтрации с
предельным градиентом давления
Схема образования застойных зон
а - между двумя добывающими скважинами;
b - при пятиточечной расстановке скважин
(1 - нагнетательная скважина; 2 - добывающая
скважина; 3 - зона застоя)
Отношение незаштрихованных областей ко всей площади пятиточечной ячейки можно считать площадным коэффициентом
охвата пласта заводнением.
Величина застойной зоны и коэффициент охвата пласта зависят
от параметра
Коэффициент охвата пласта
Q
увеличивается с увеличением
k L
параметра
167



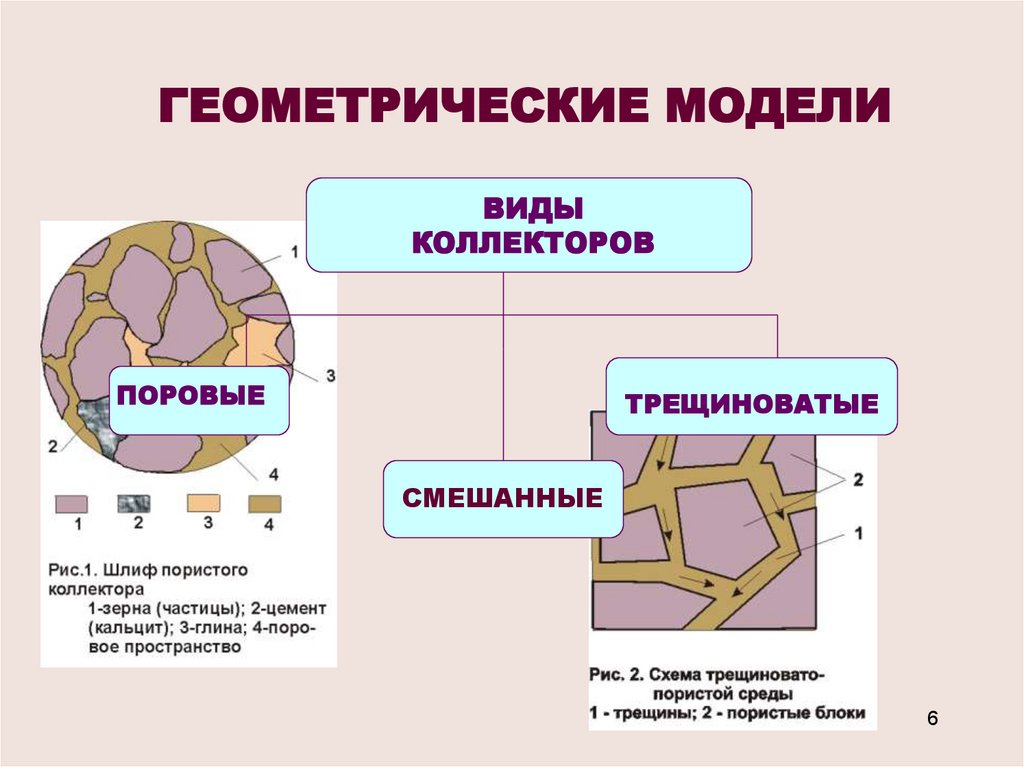
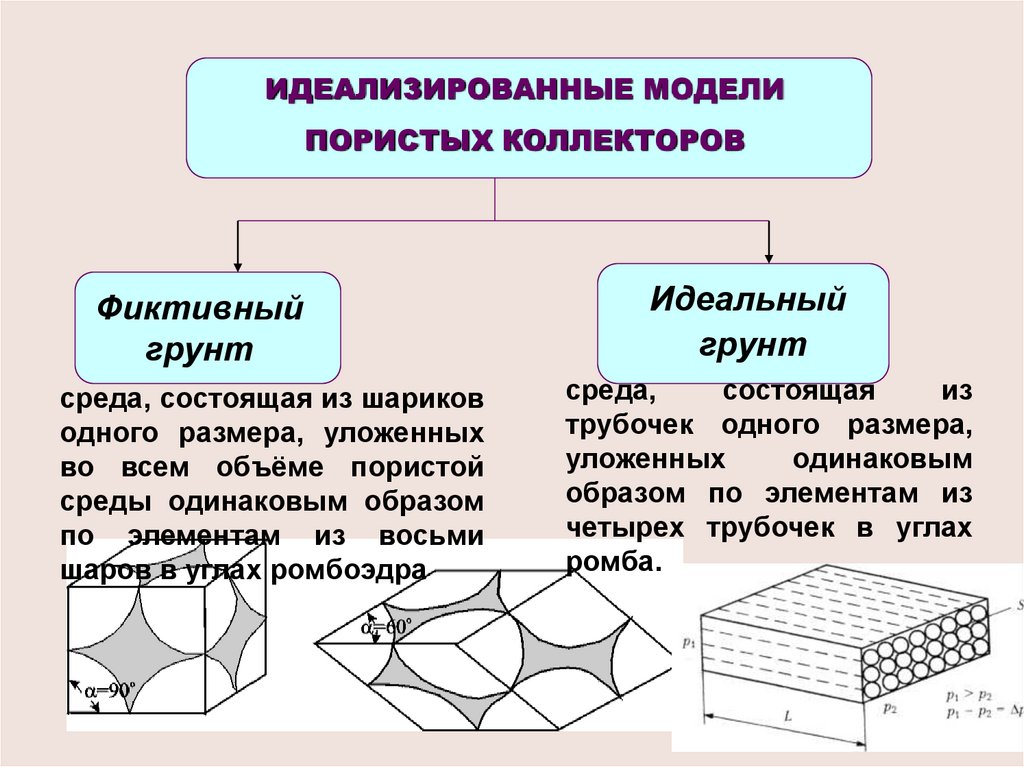

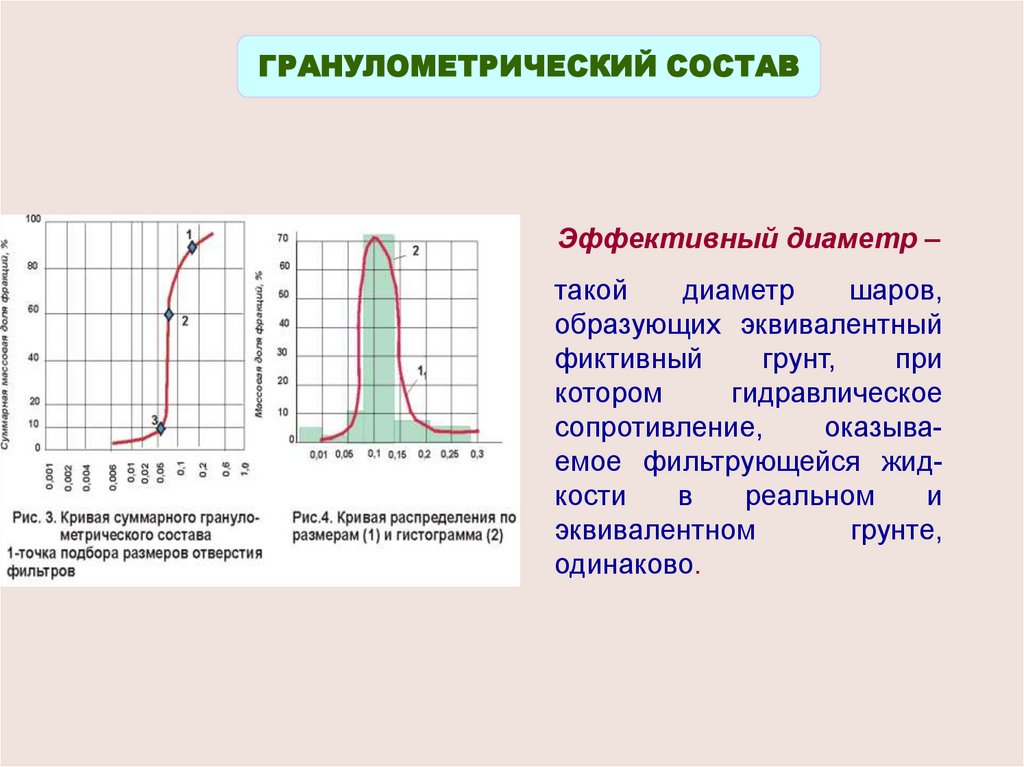
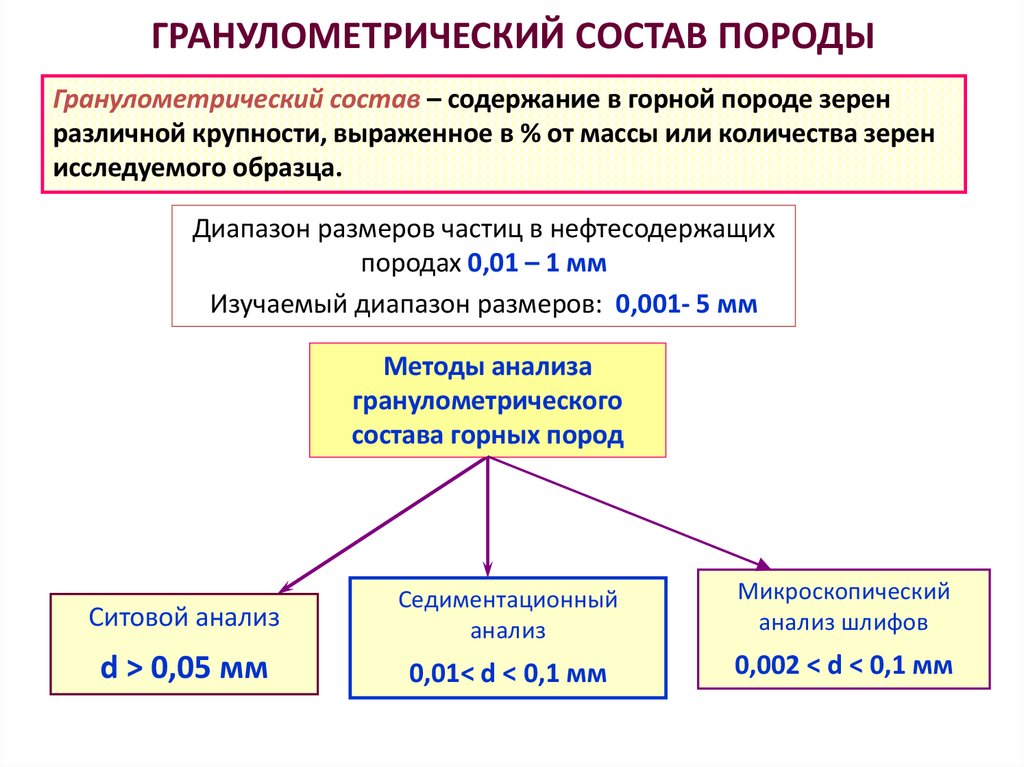
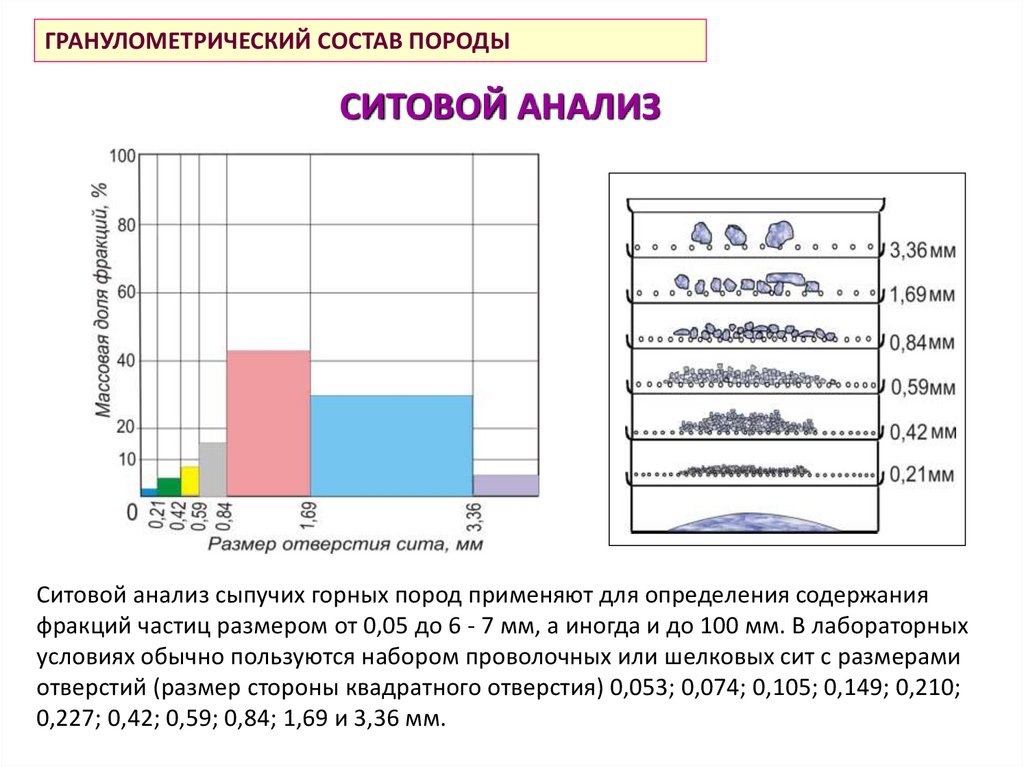
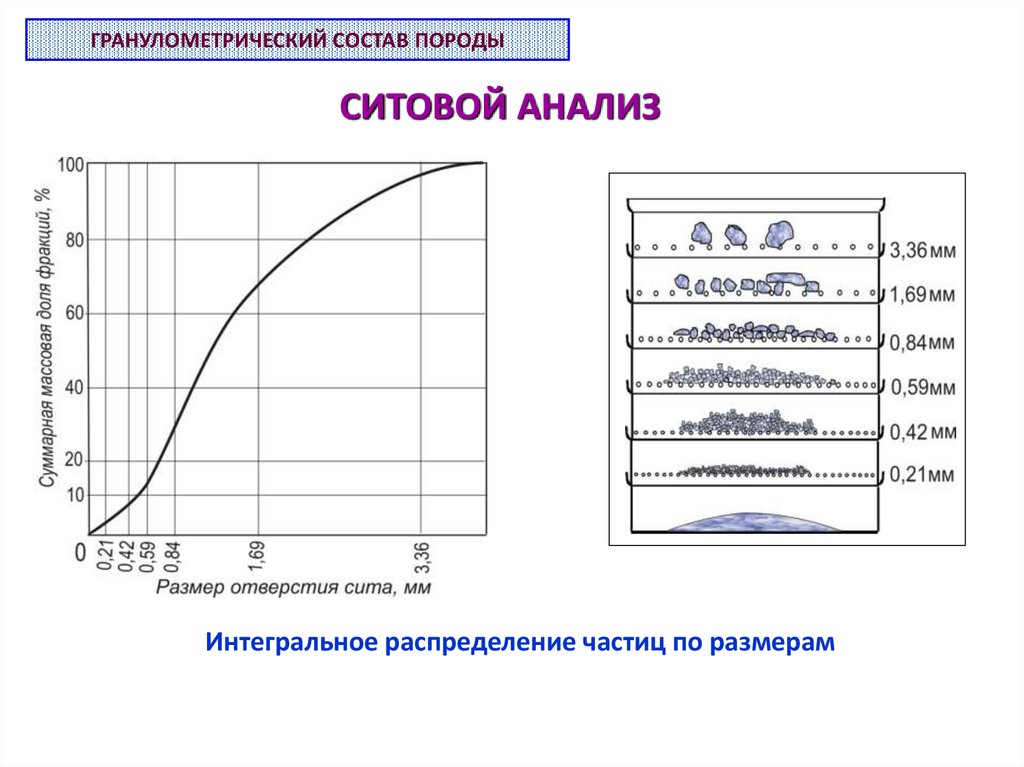
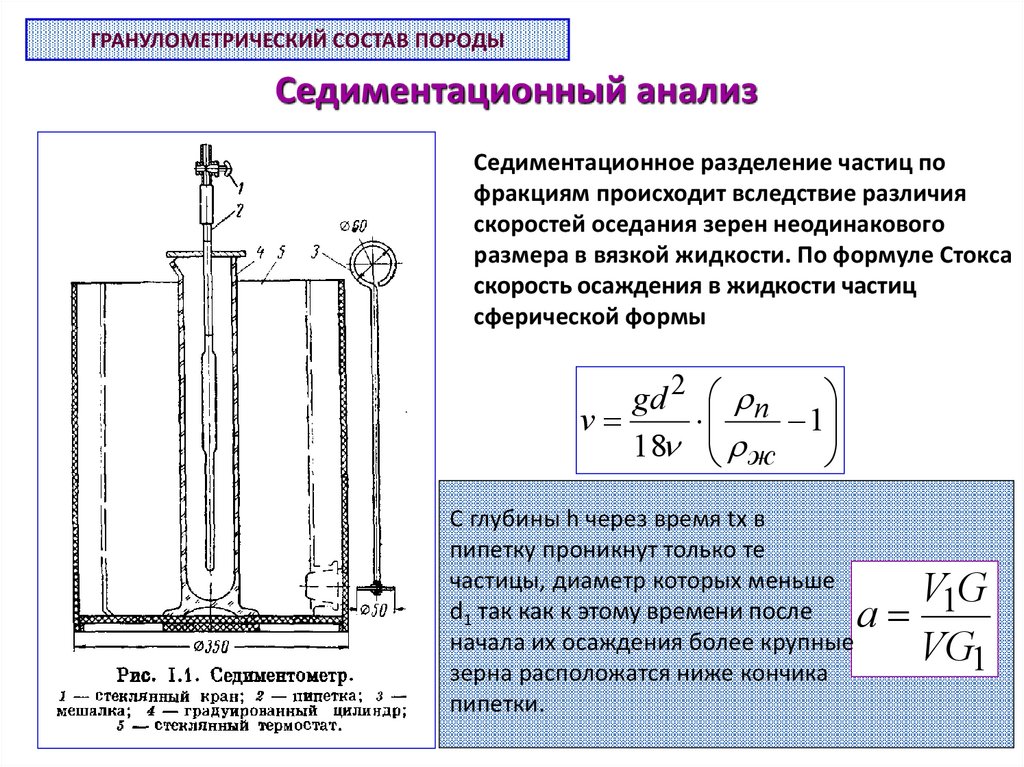

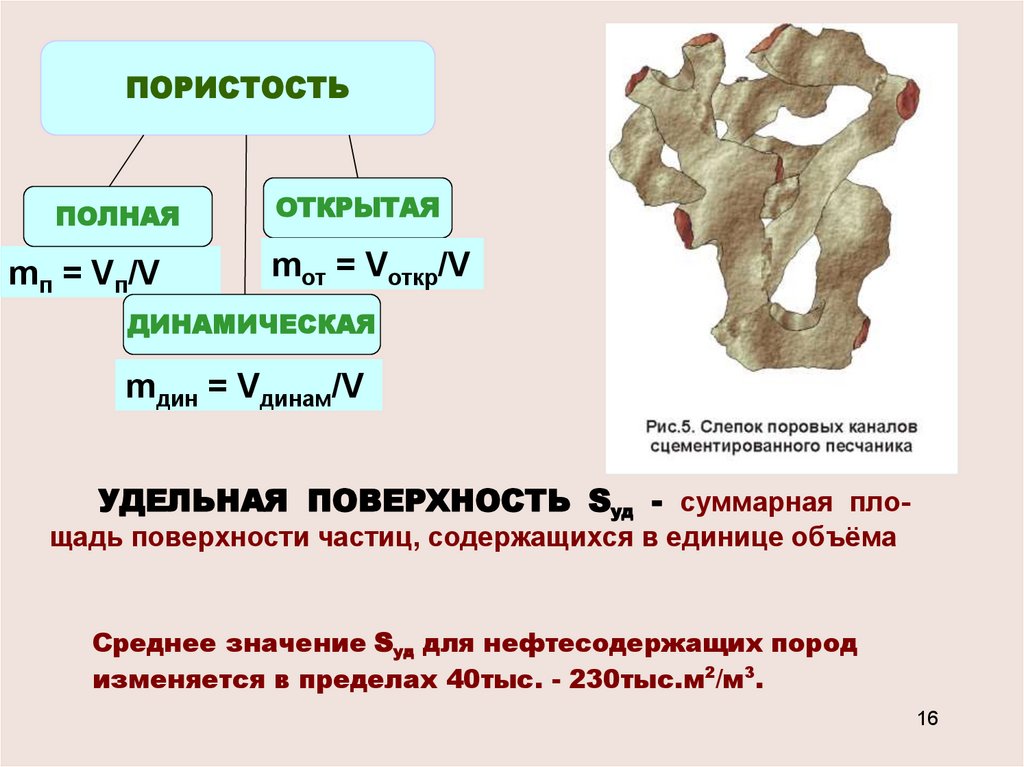
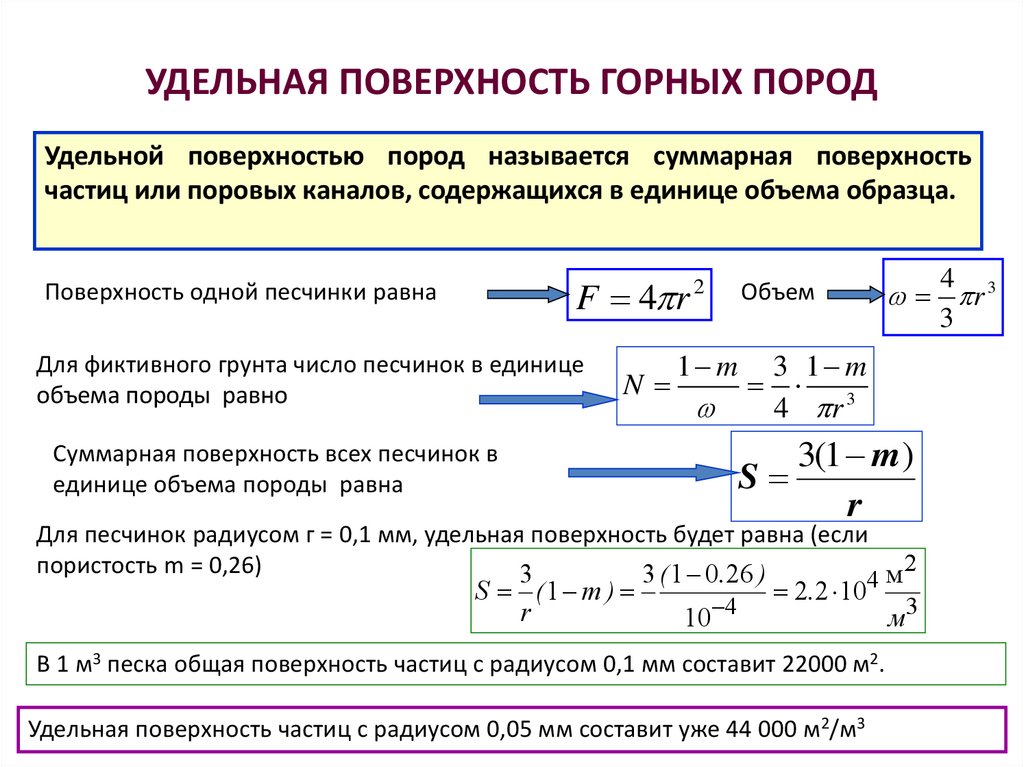
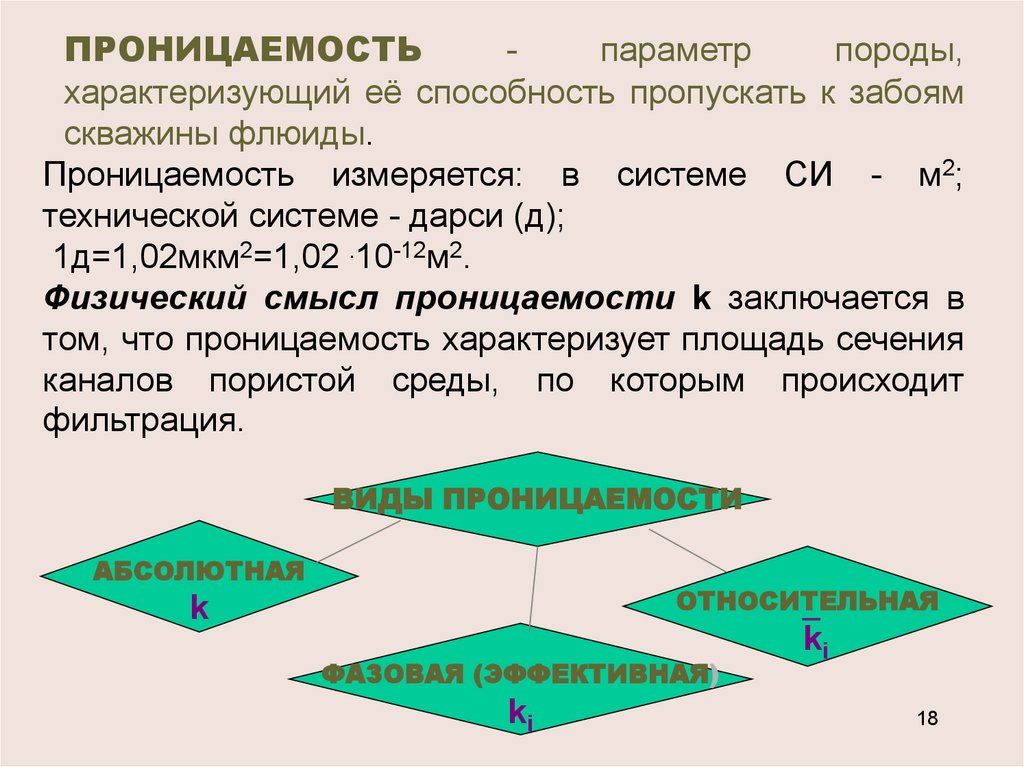

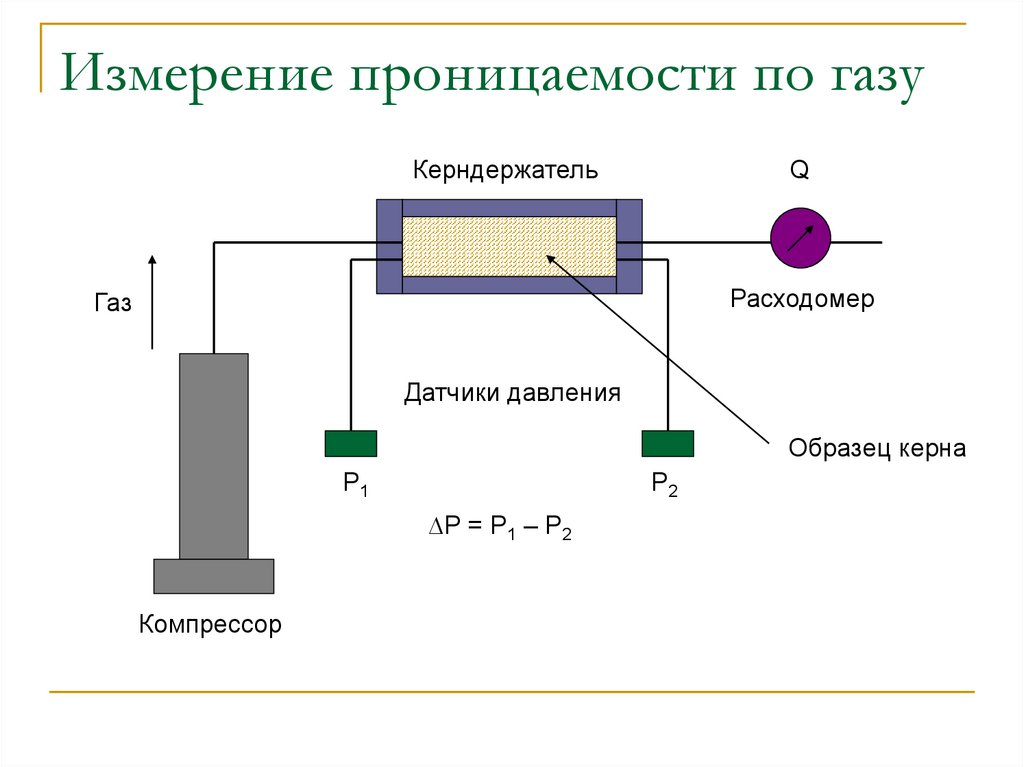

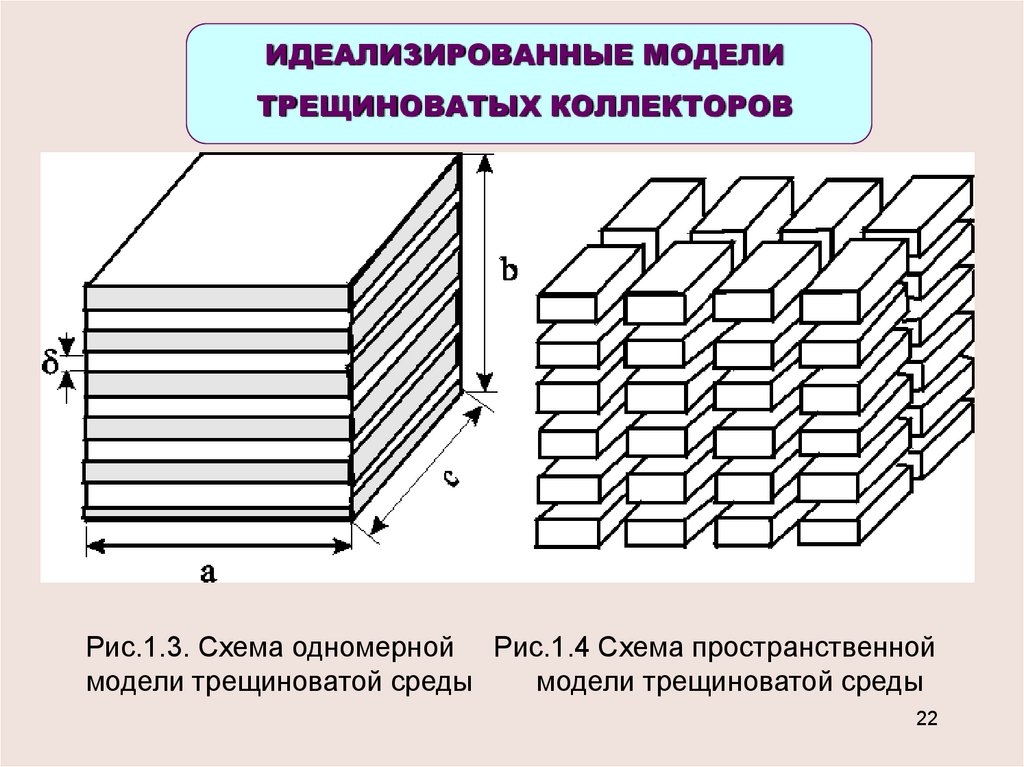
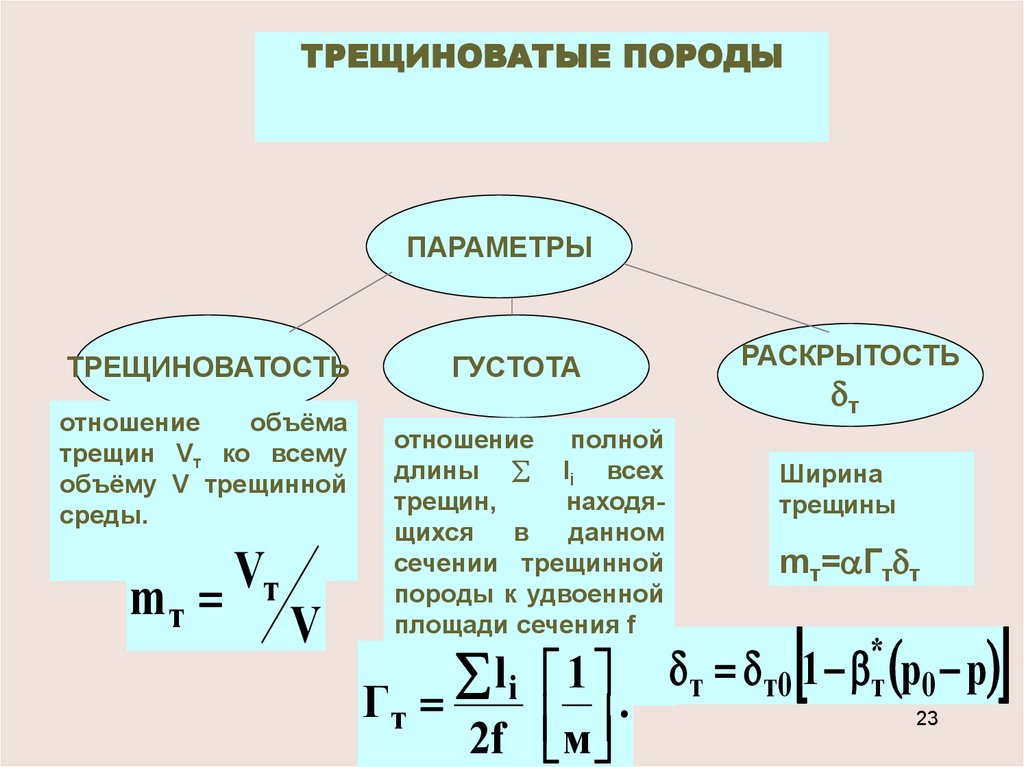
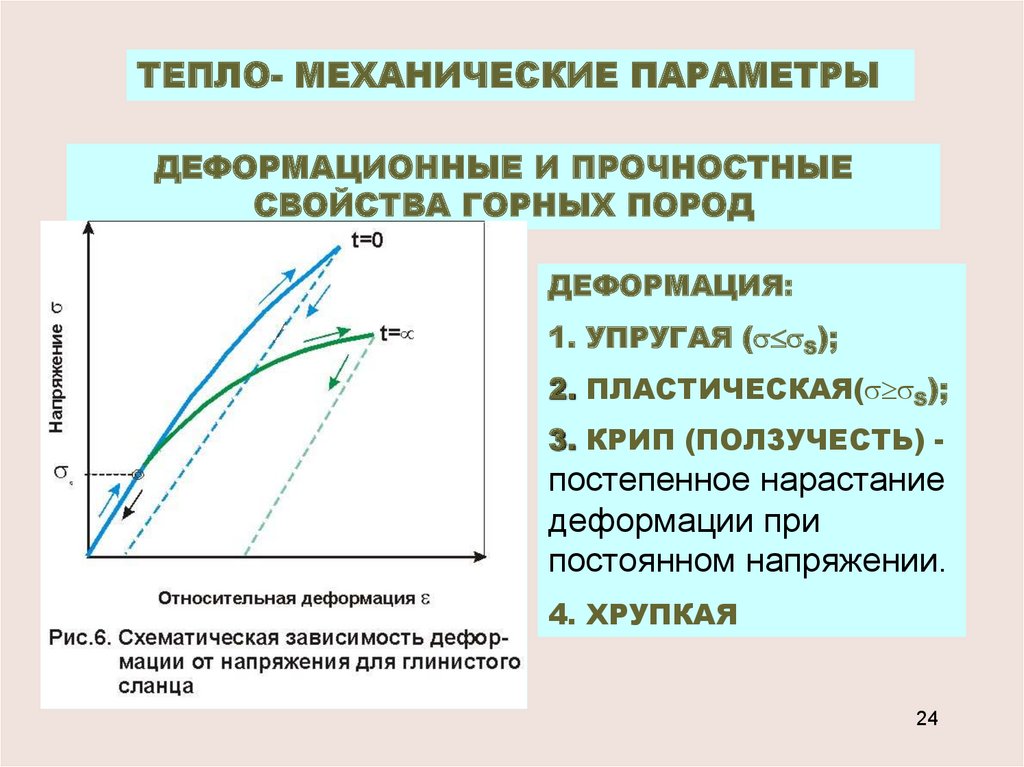
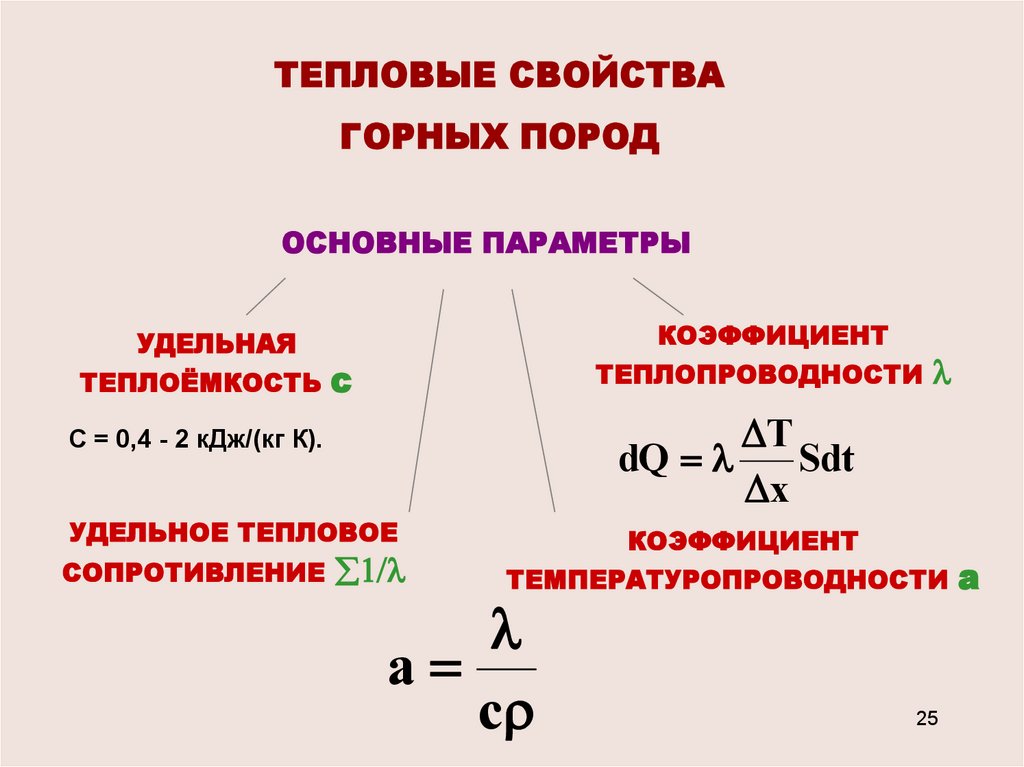


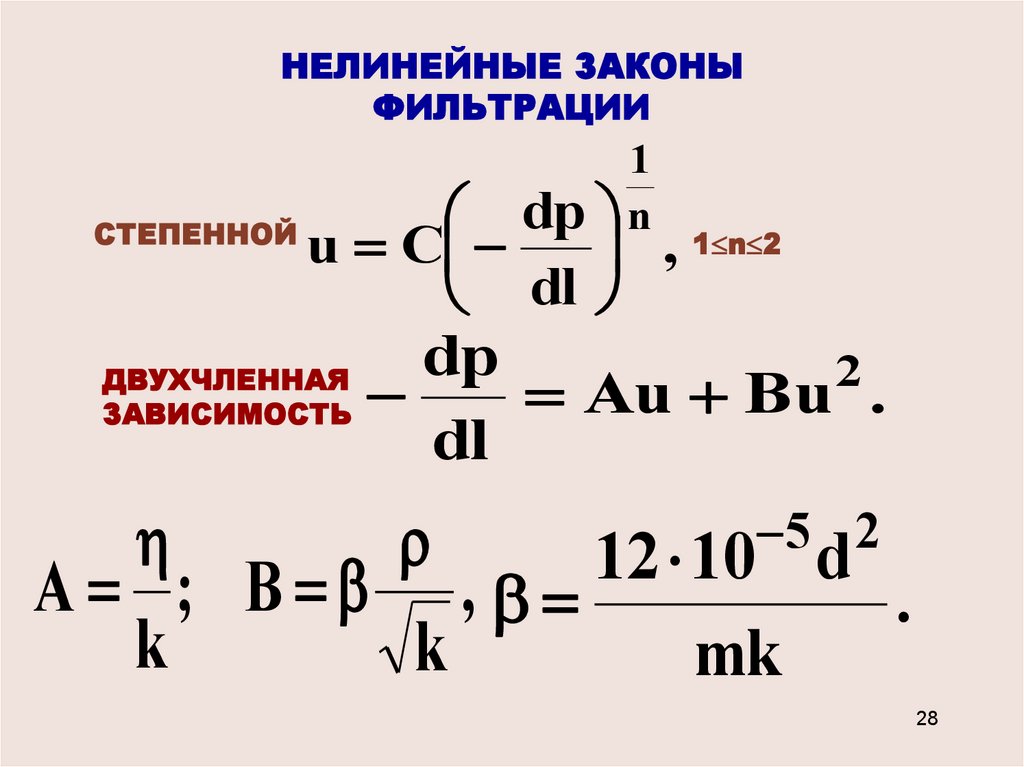









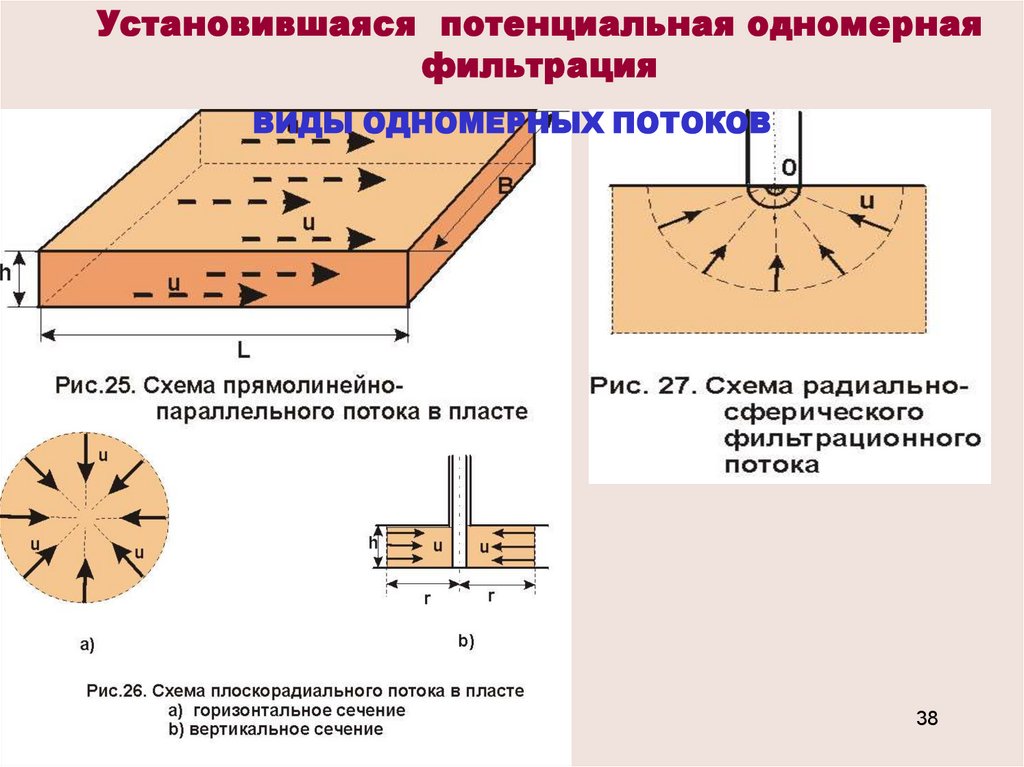















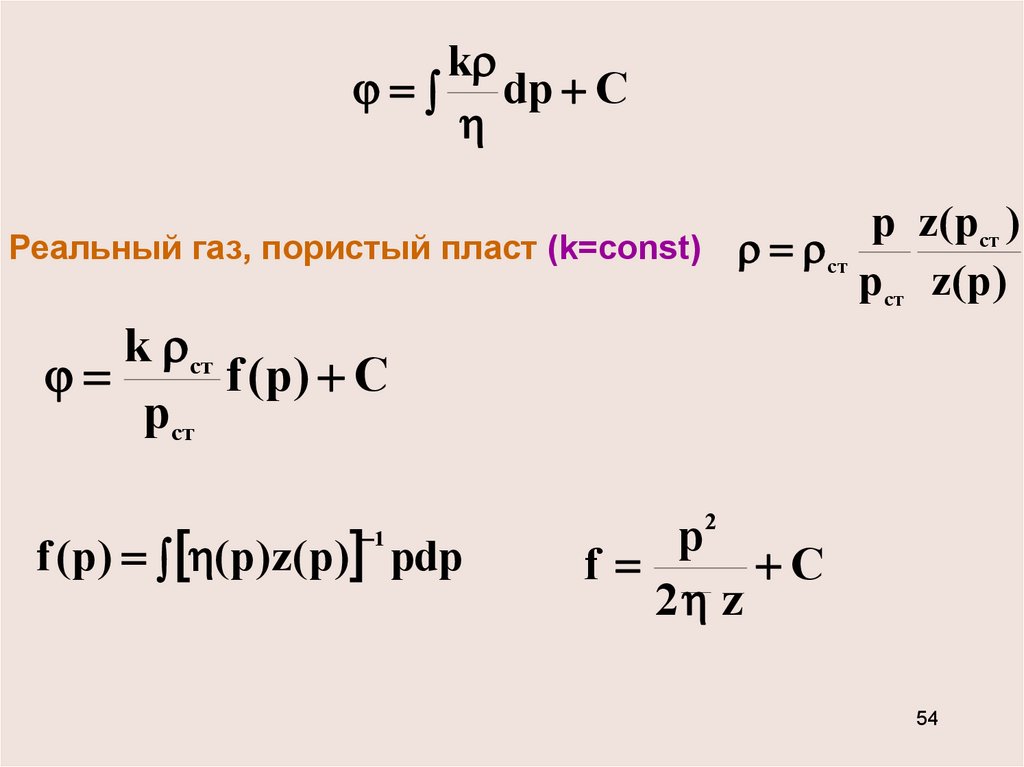



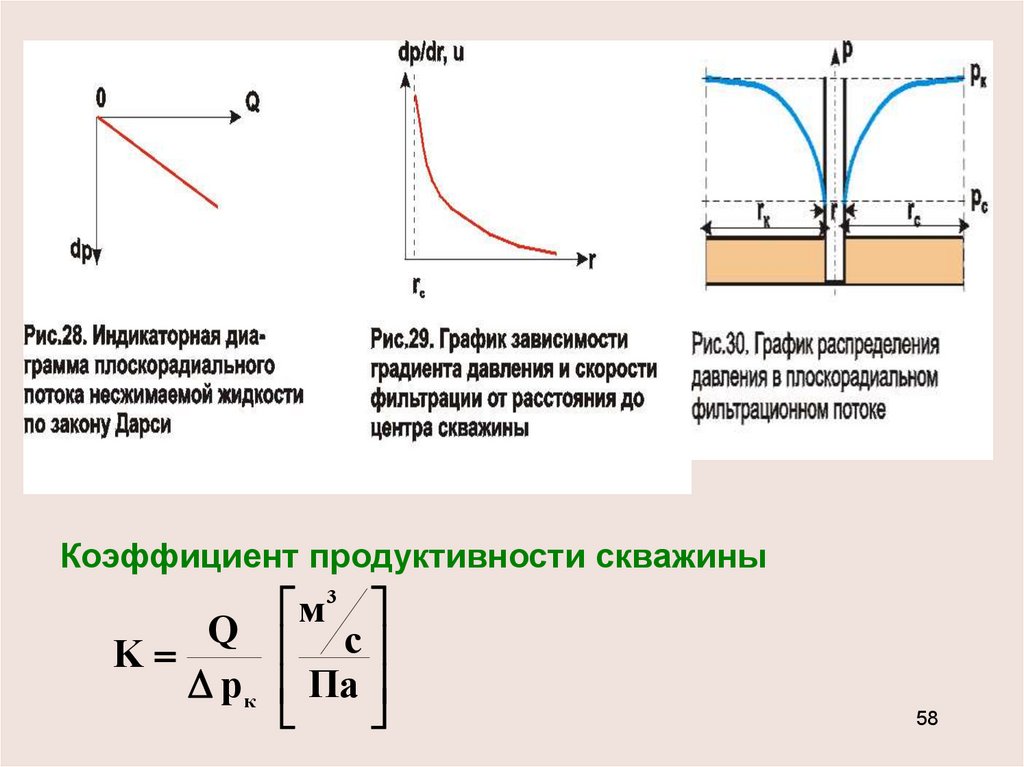

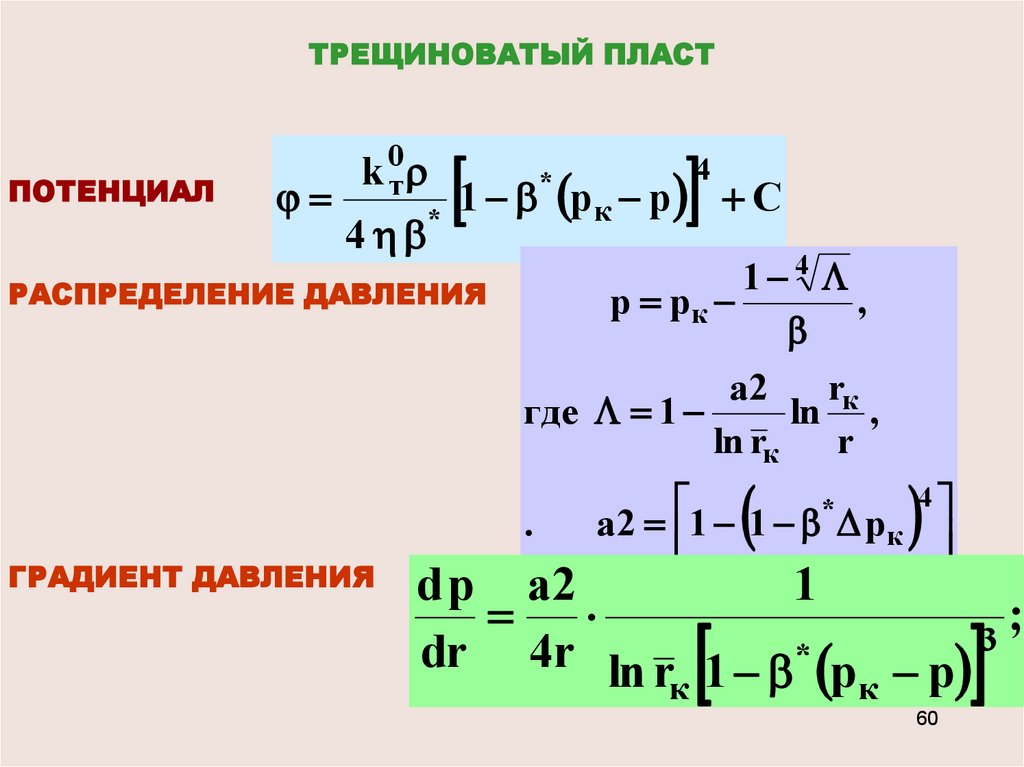
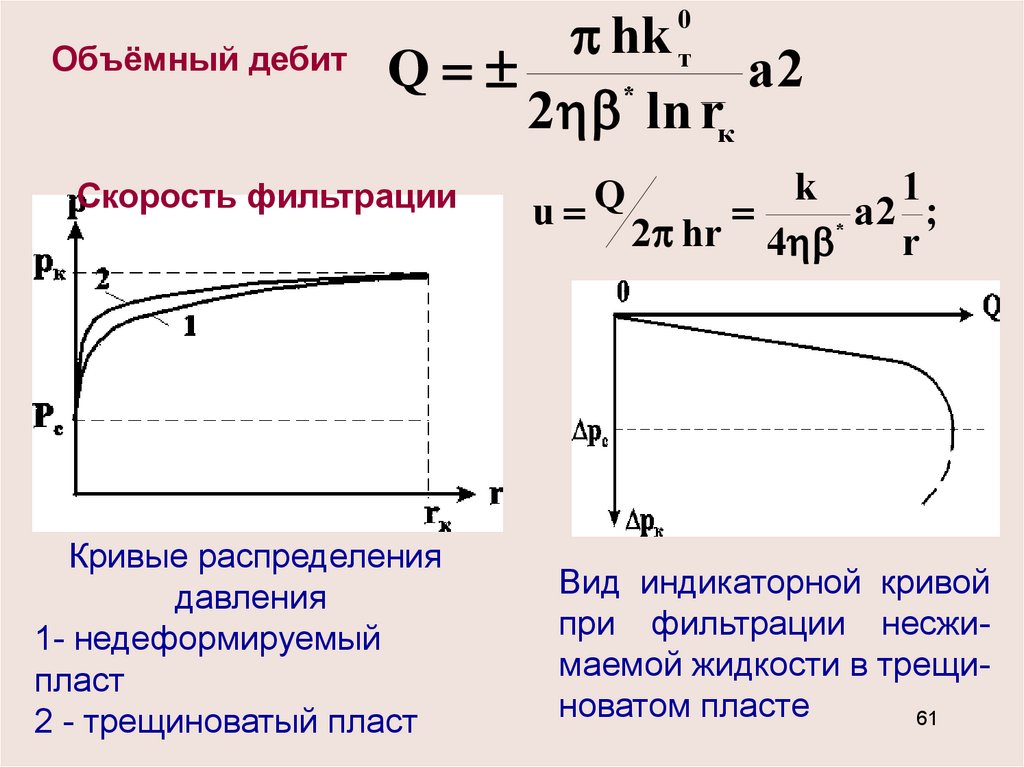



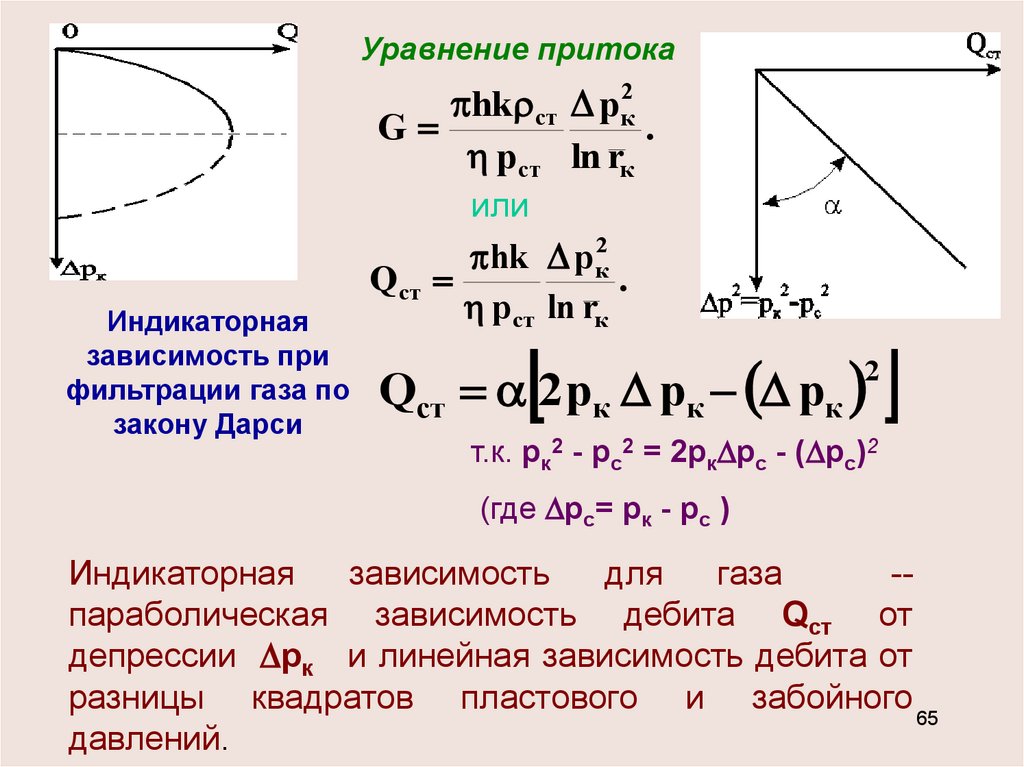














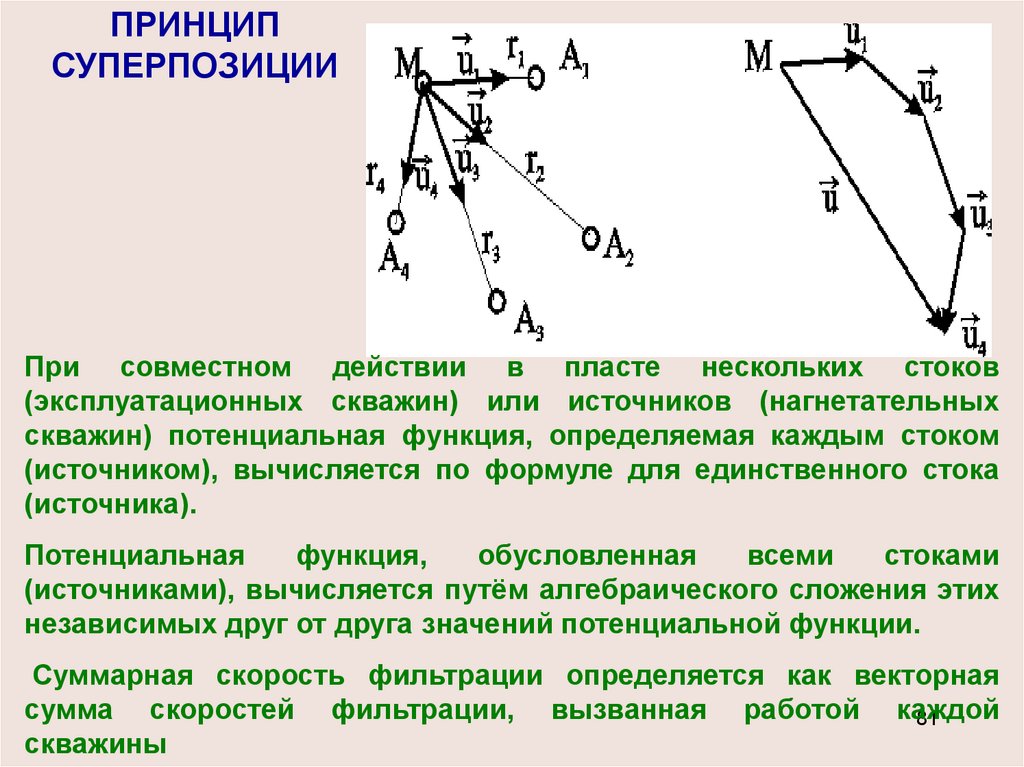

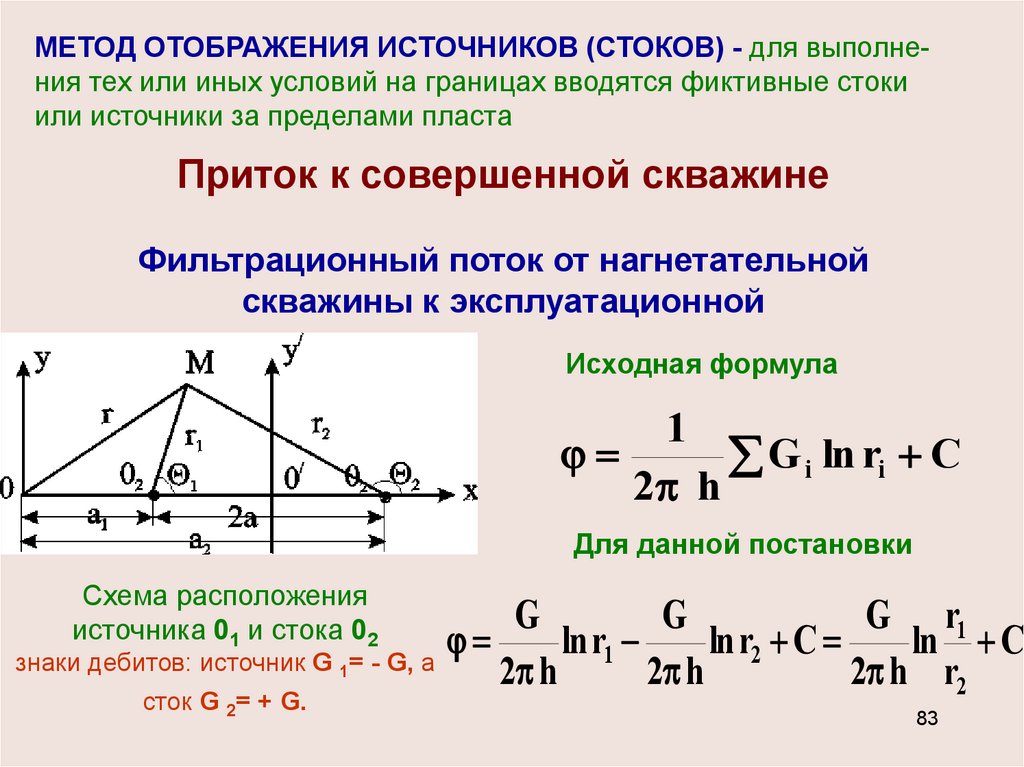
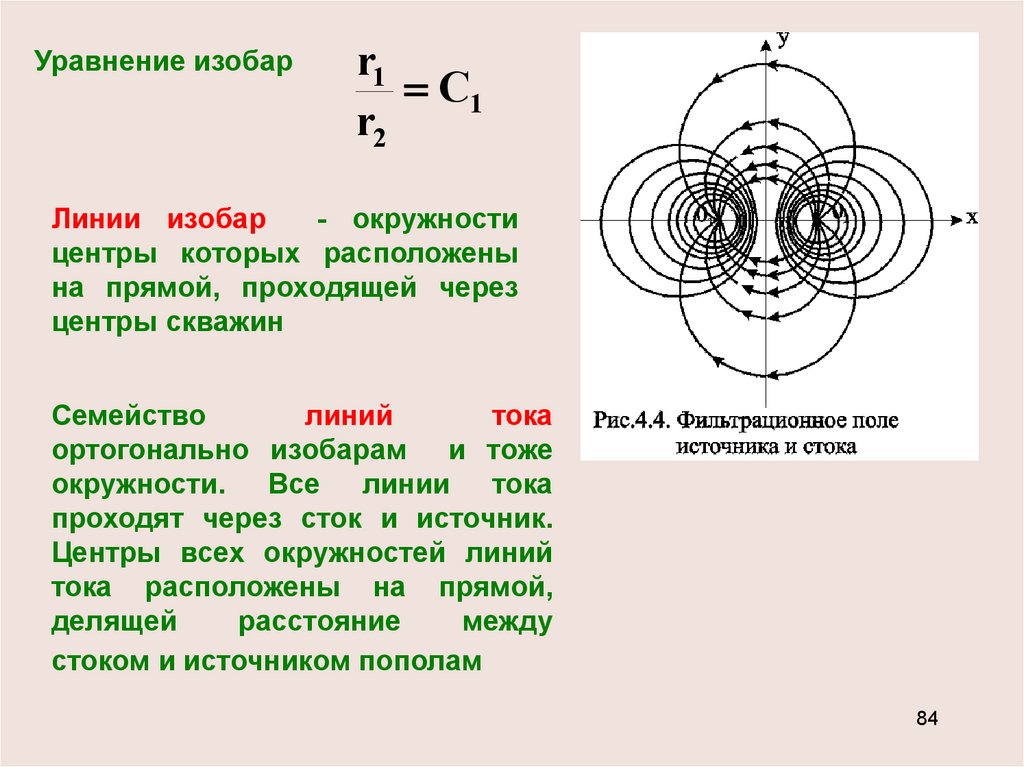


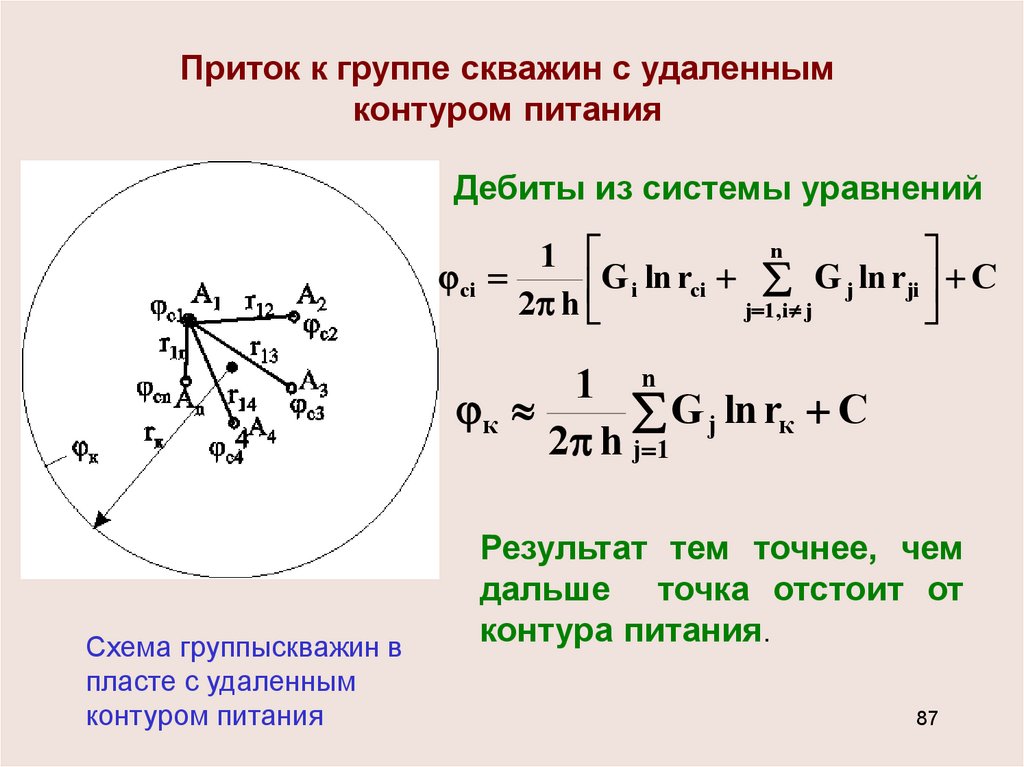

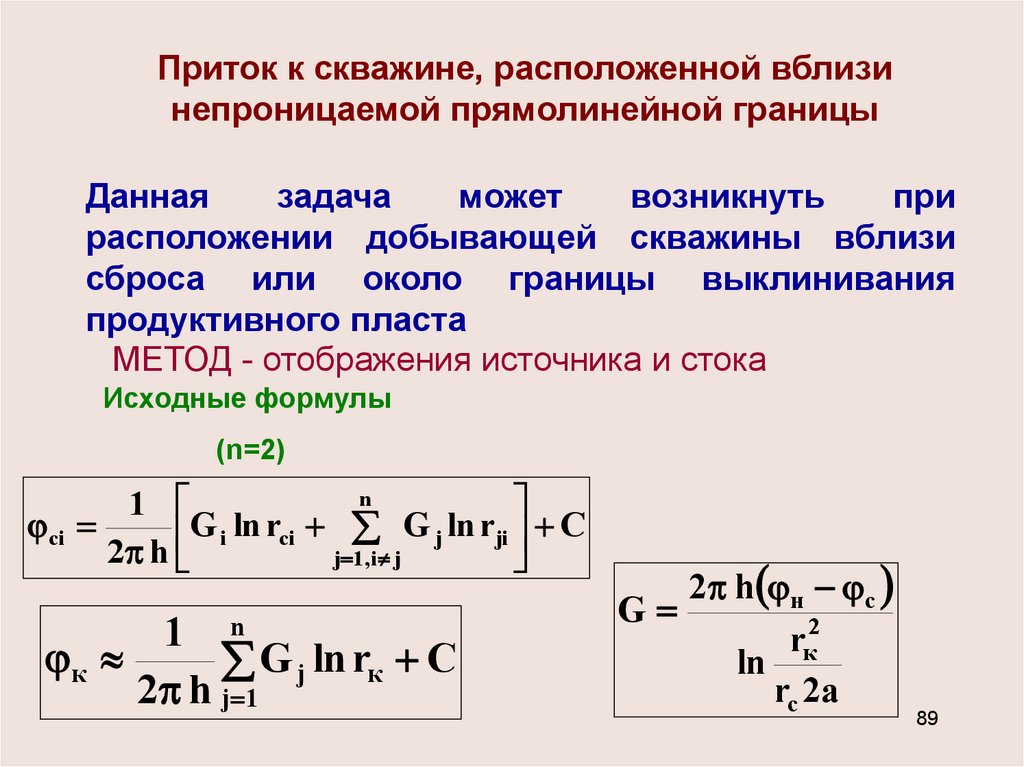
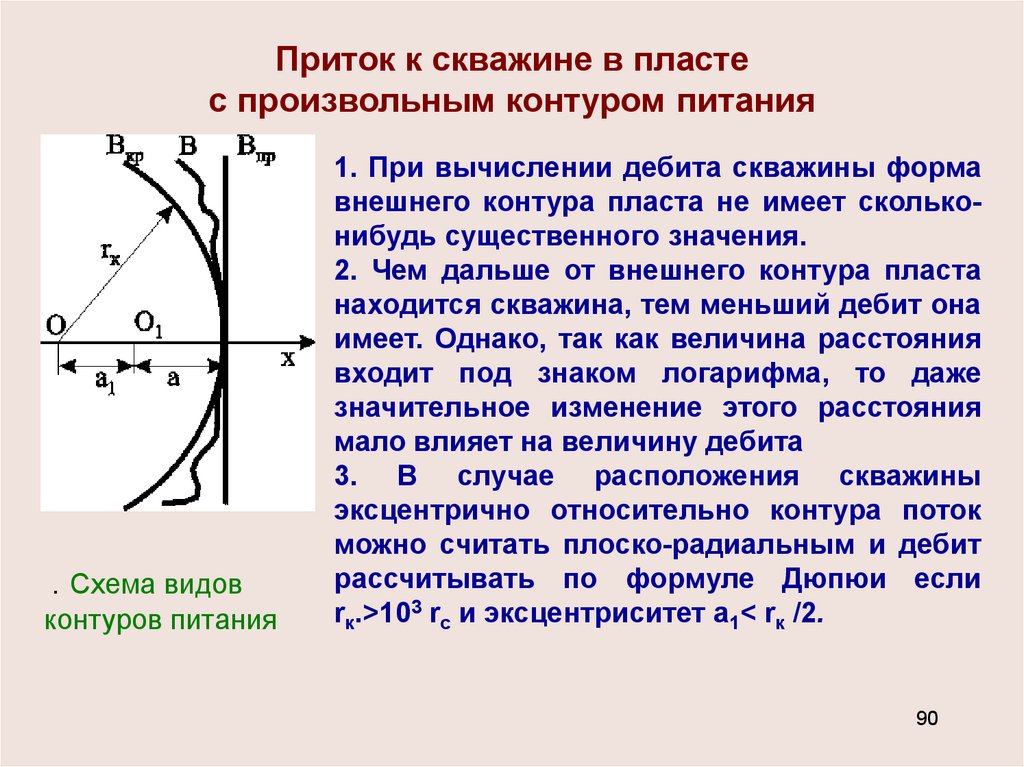
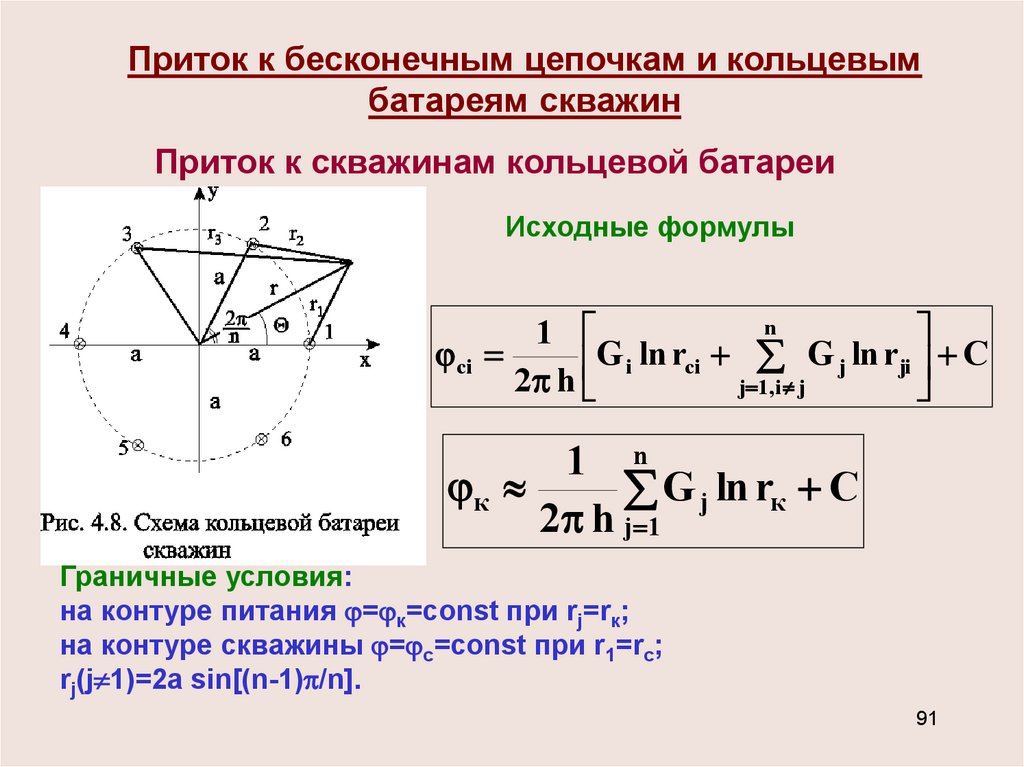

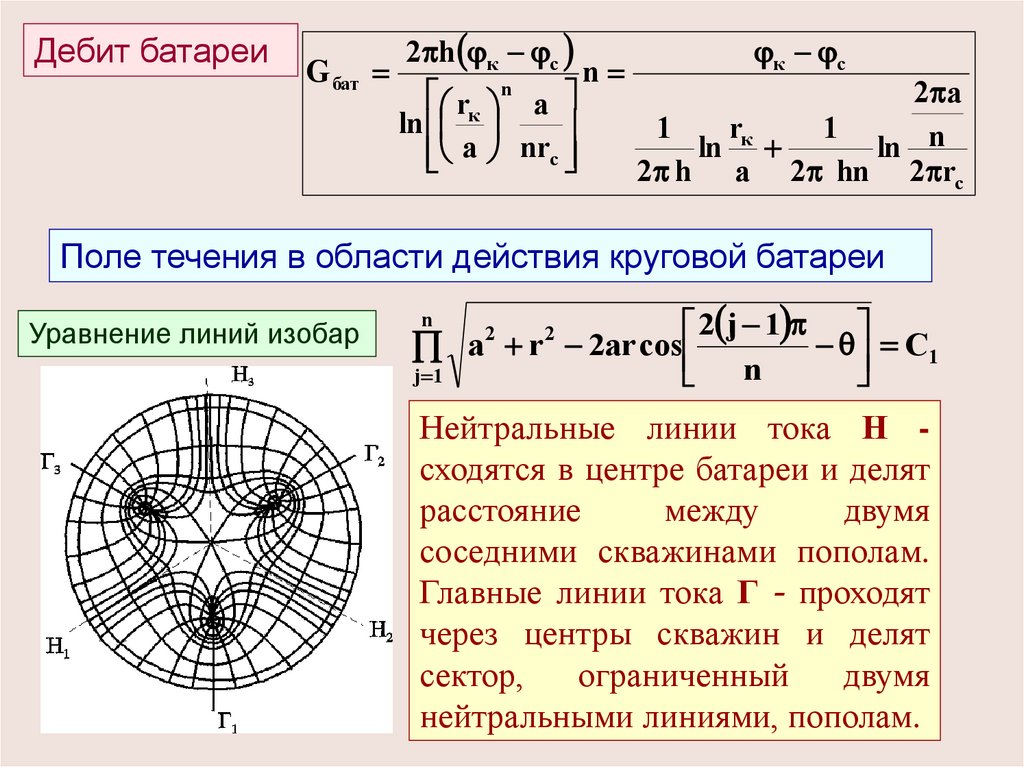








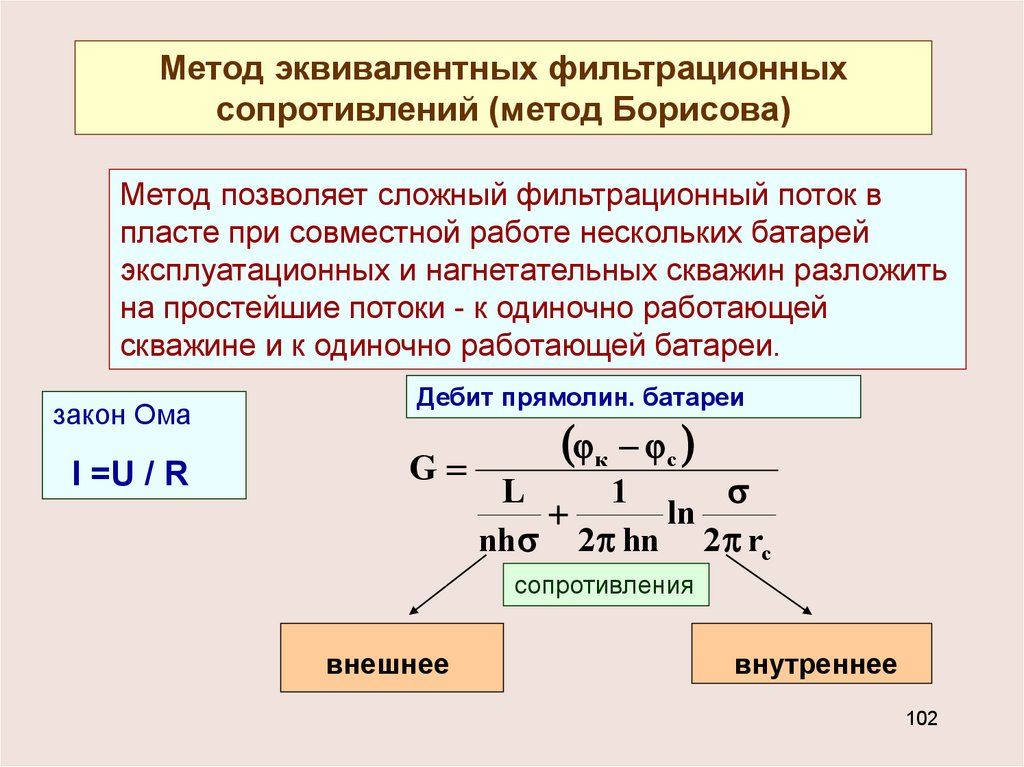
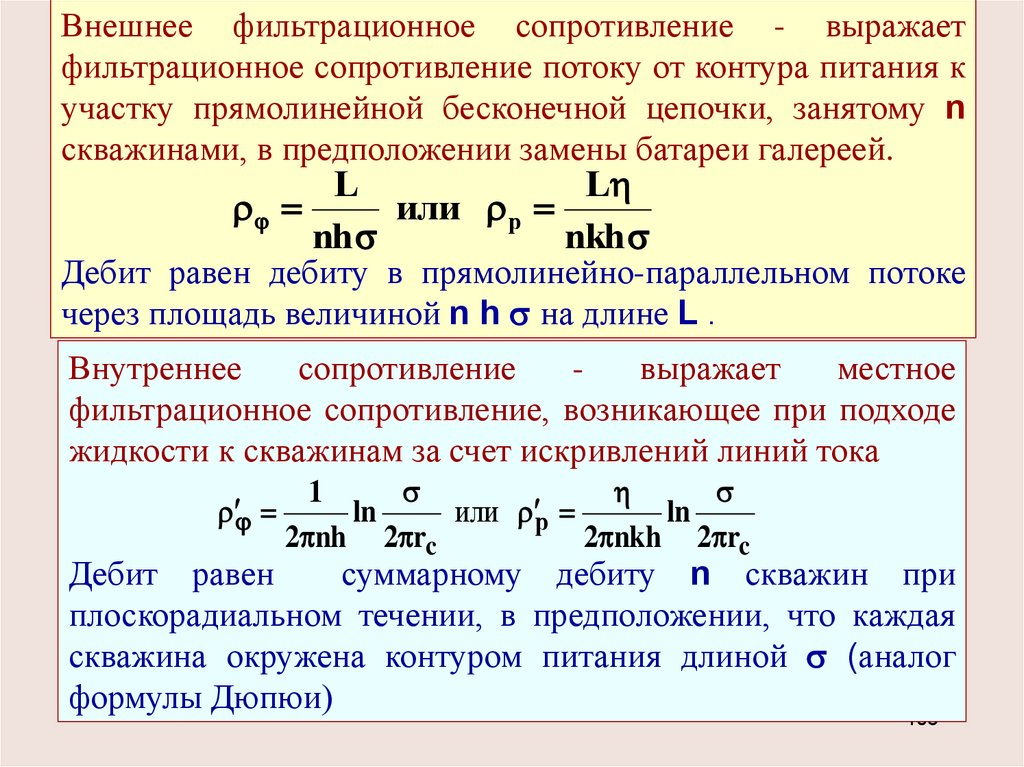
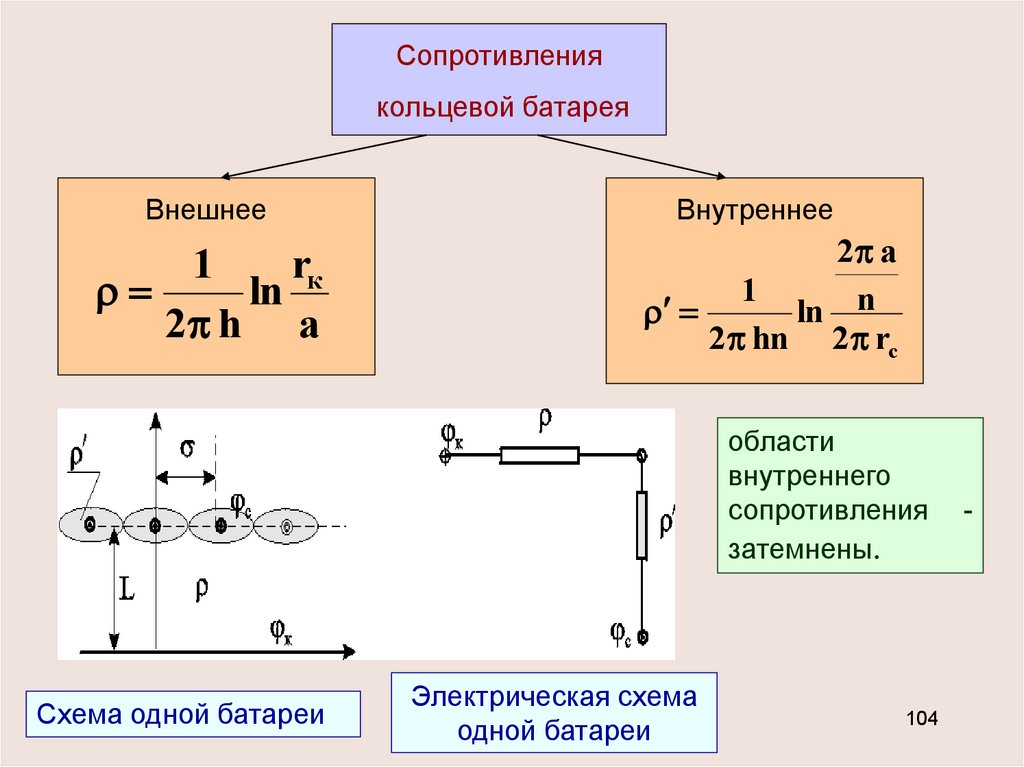
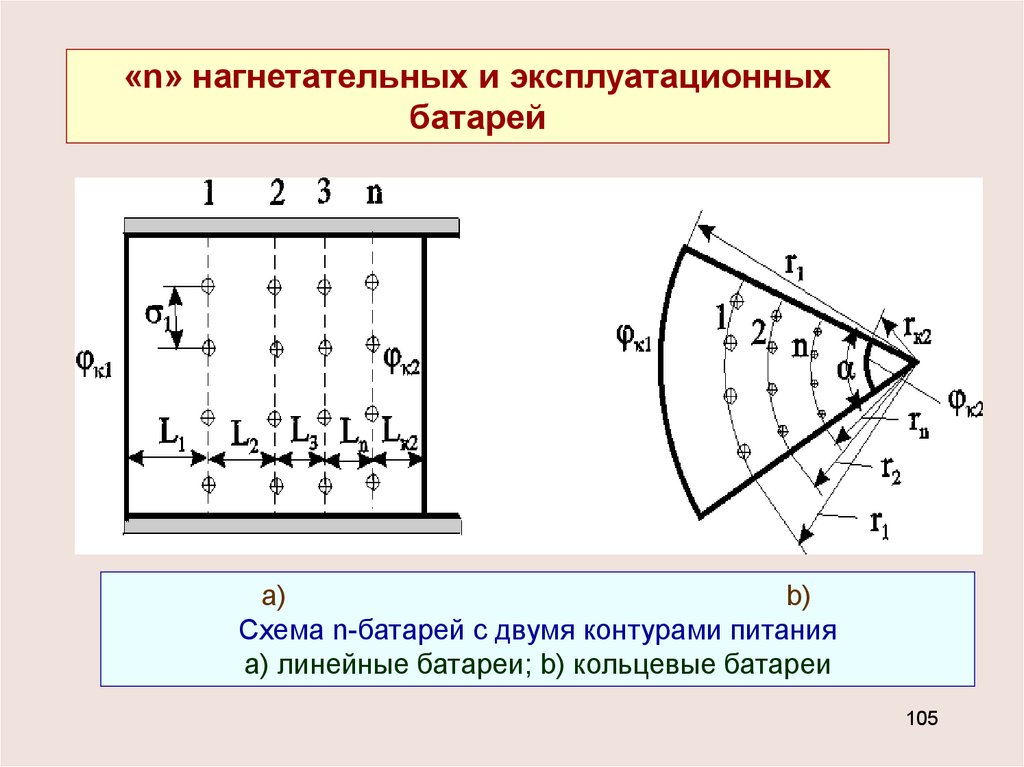
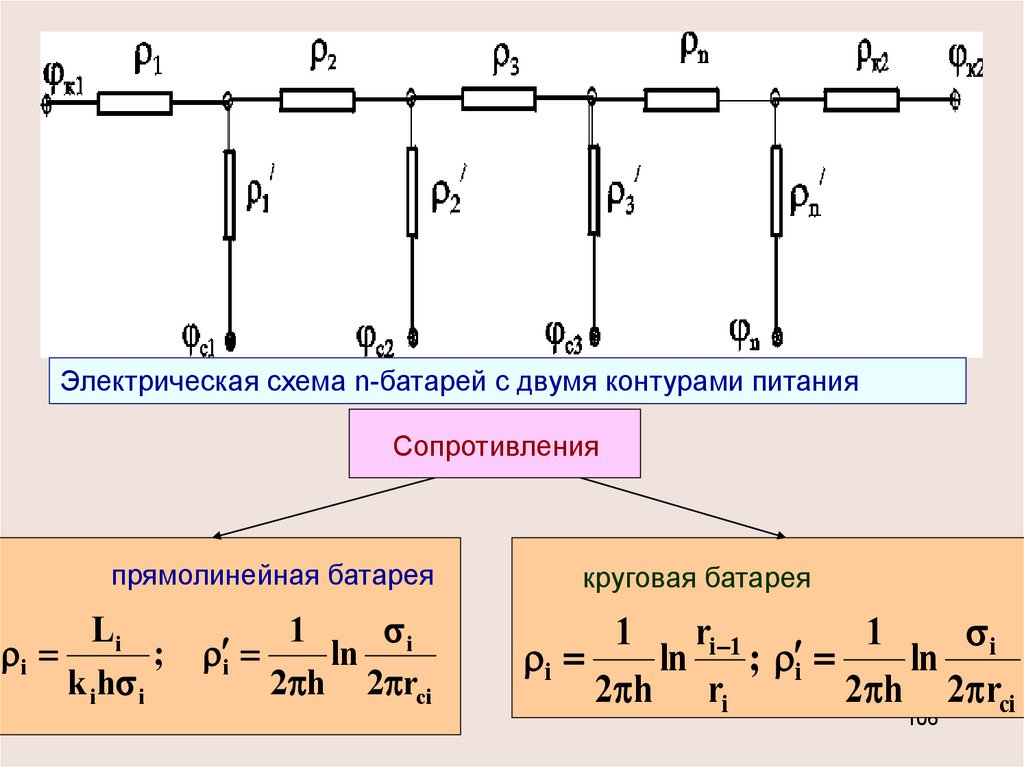
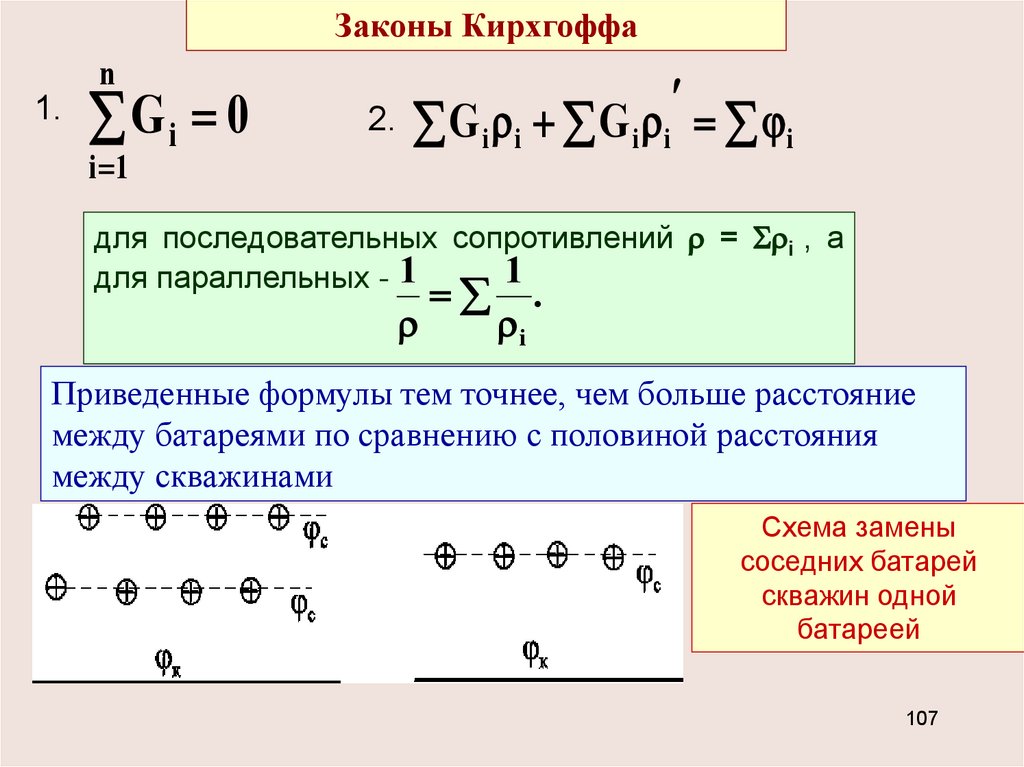
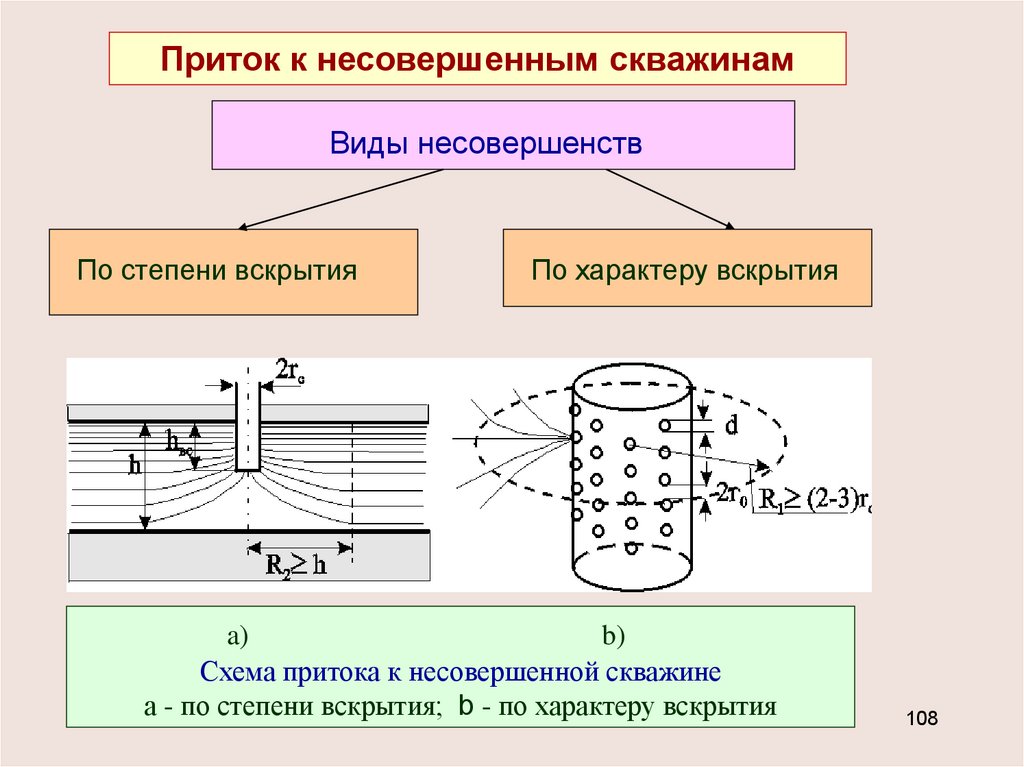

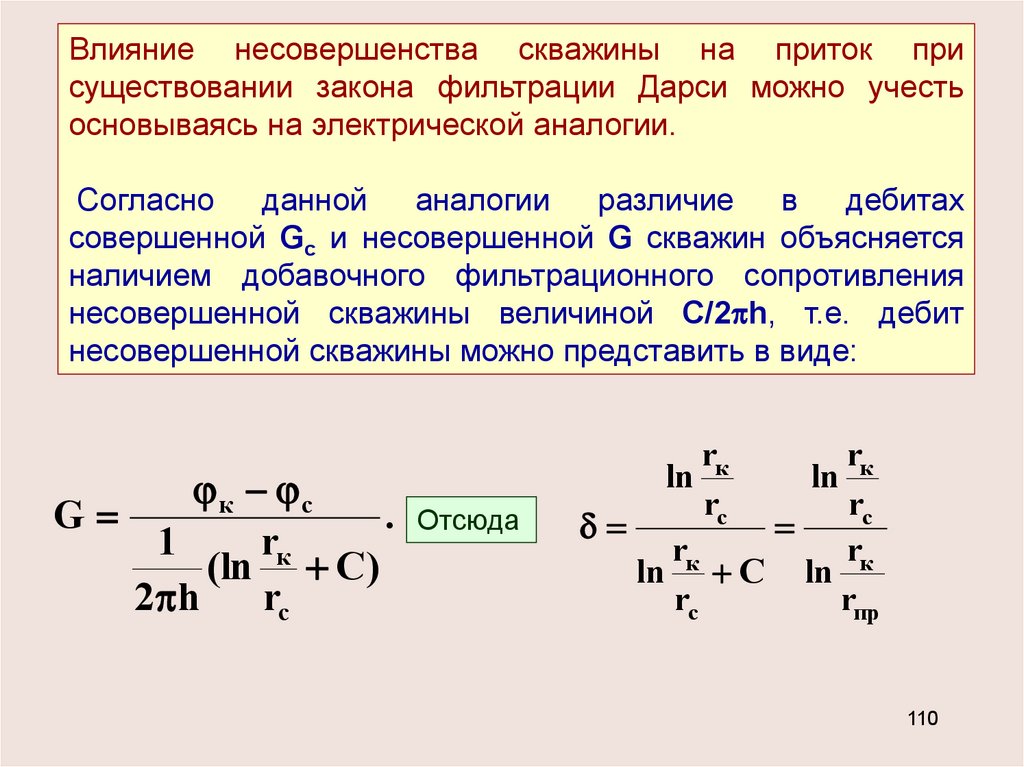

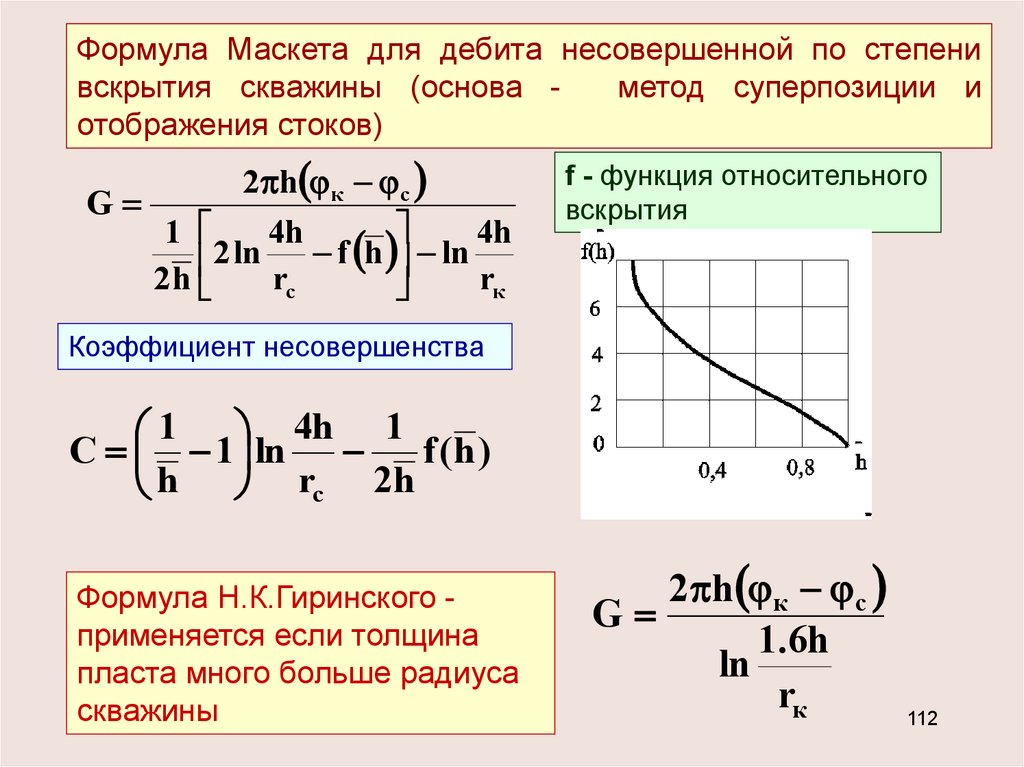


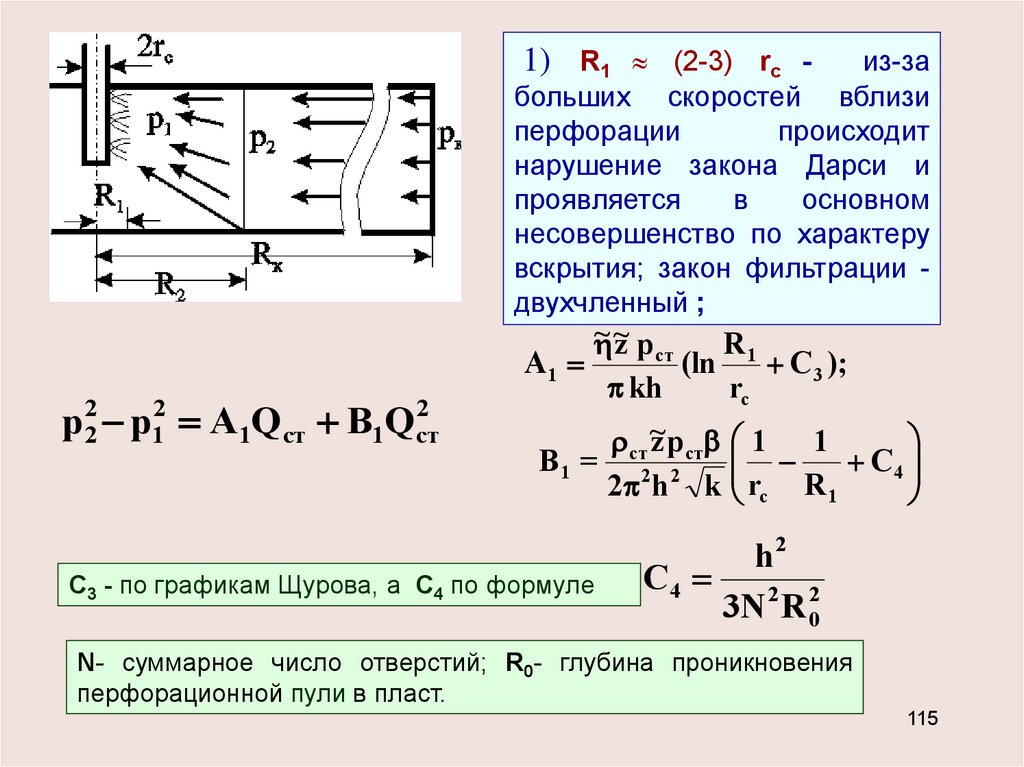



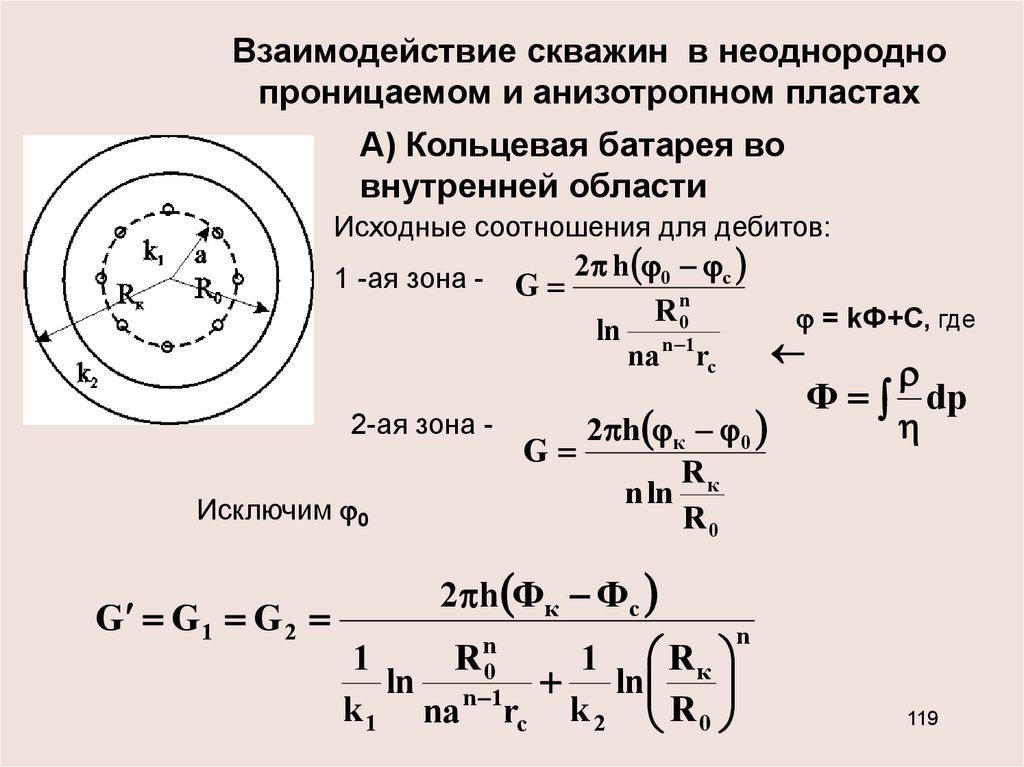



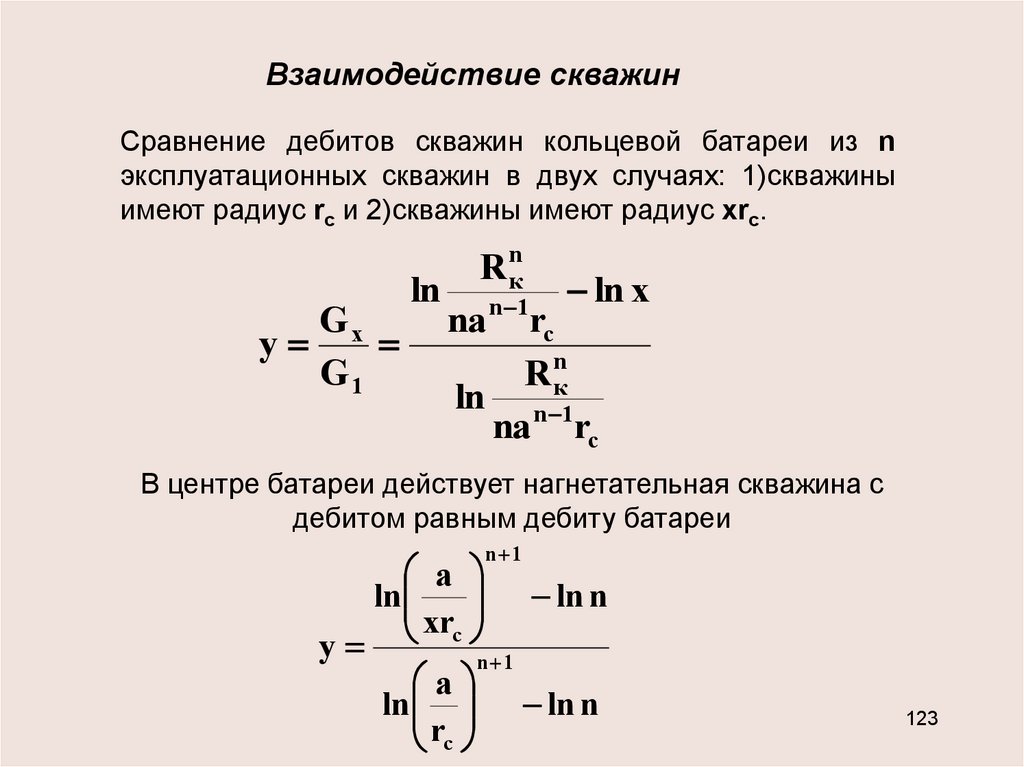








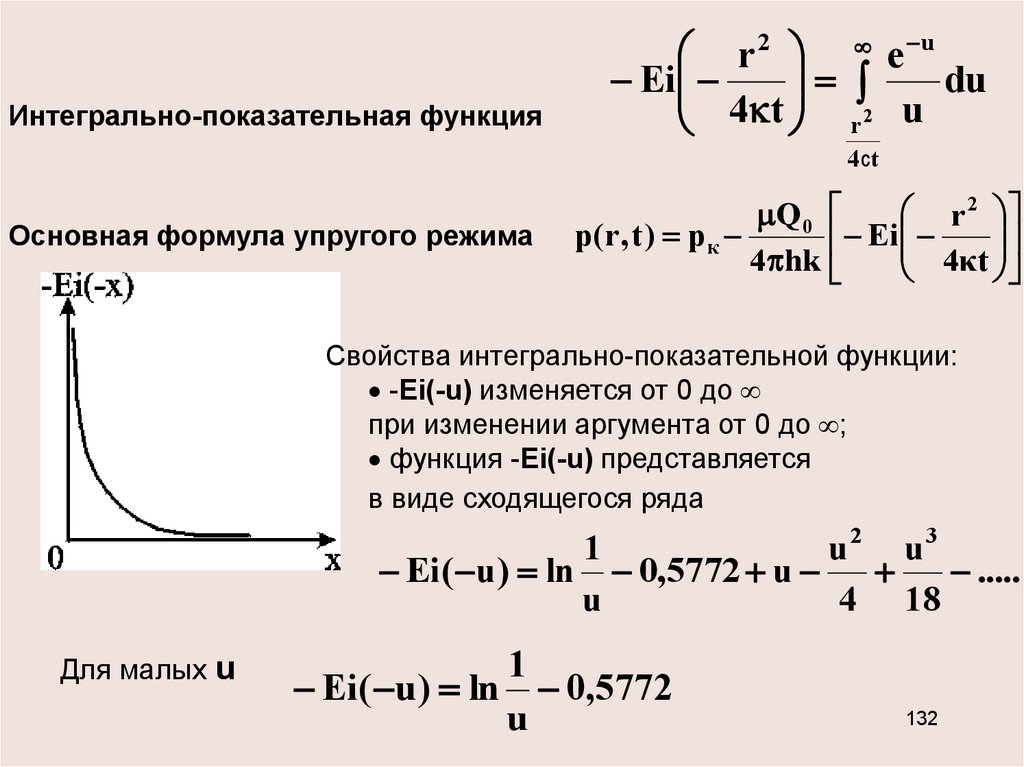


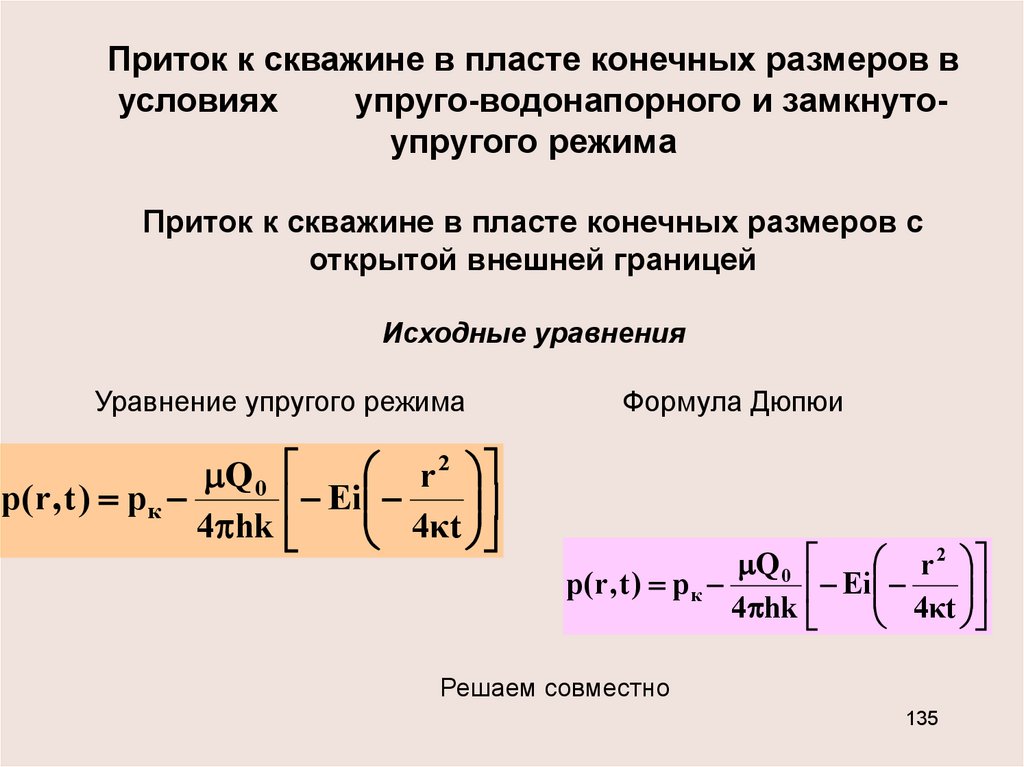
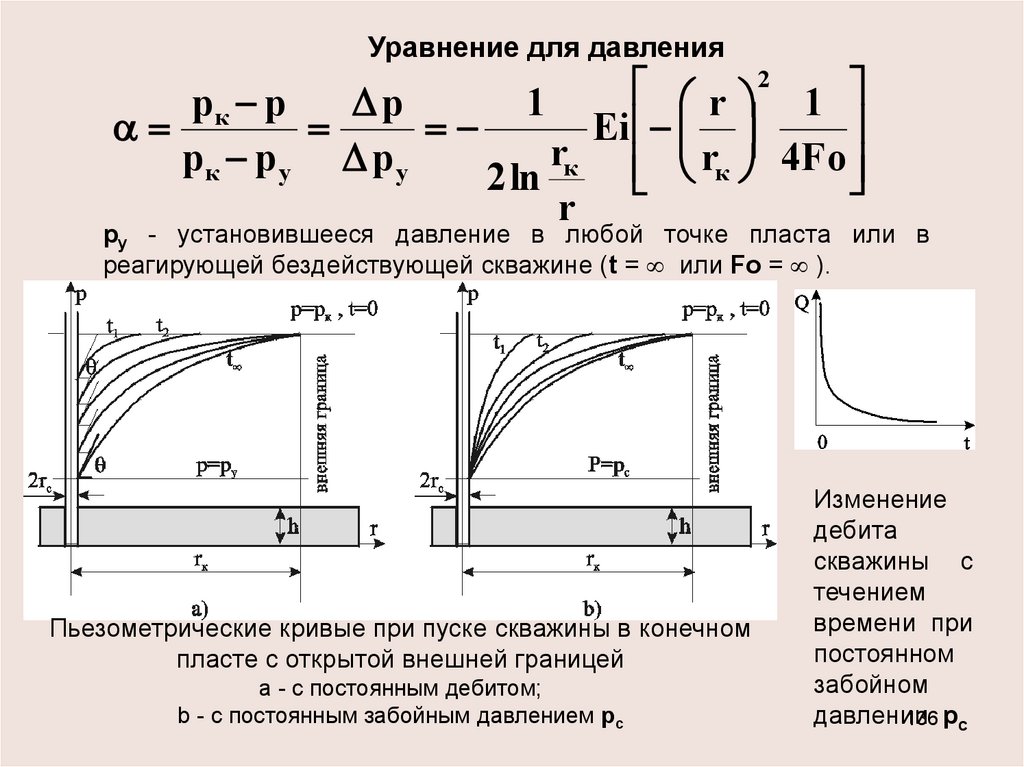
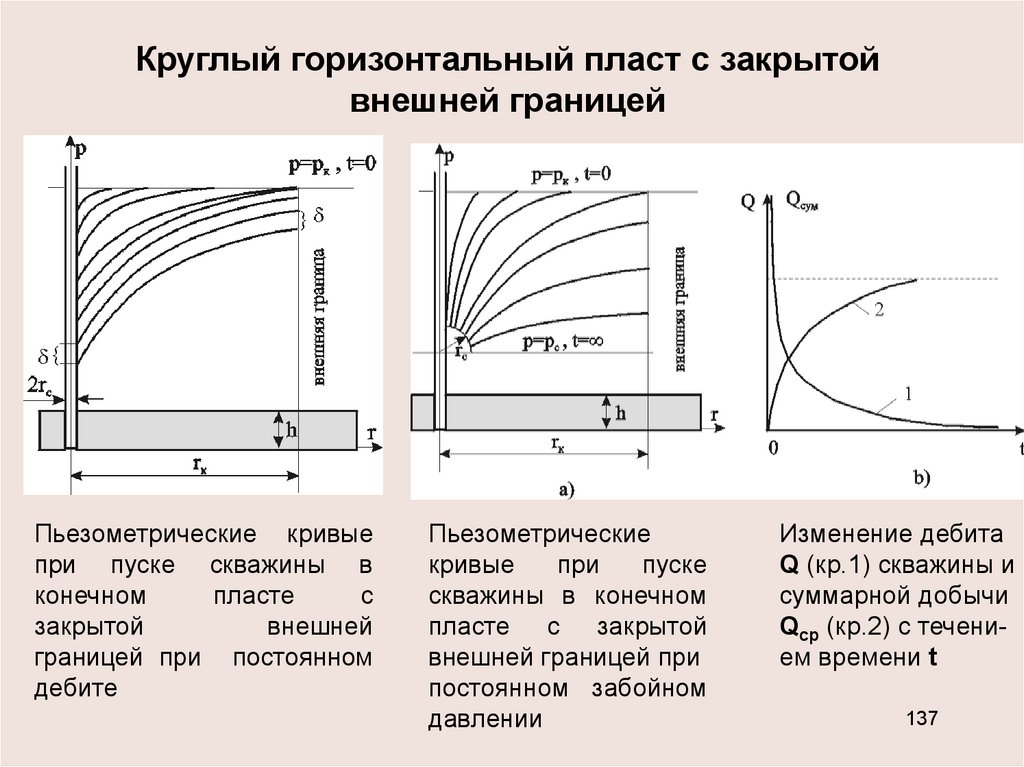



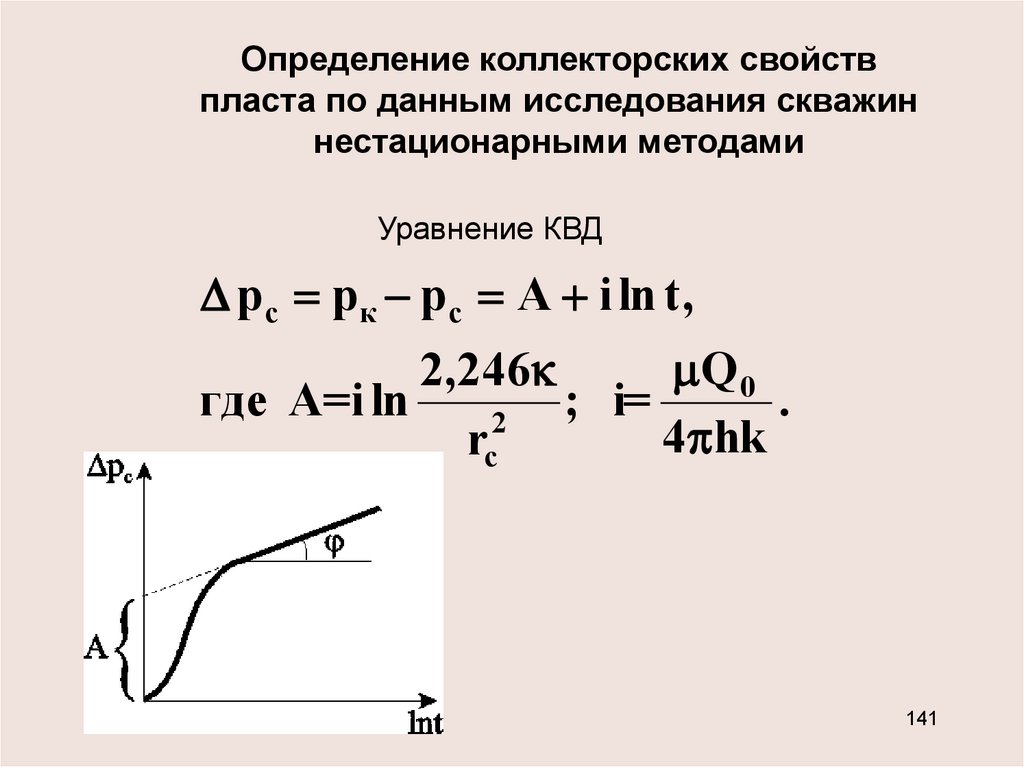
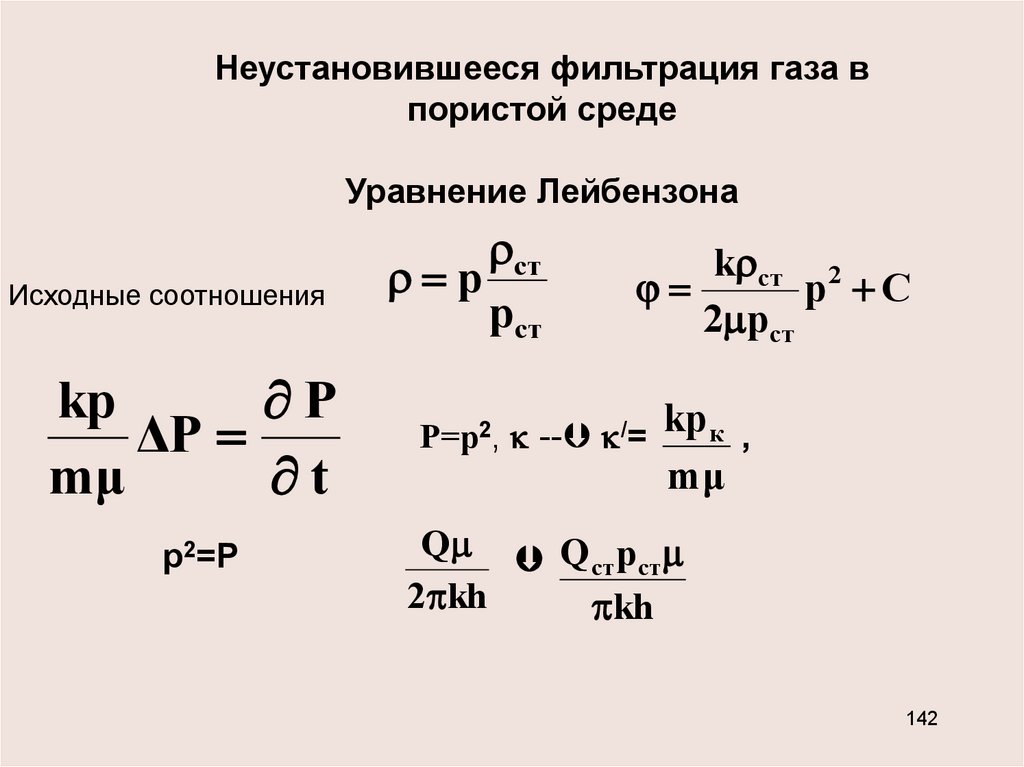

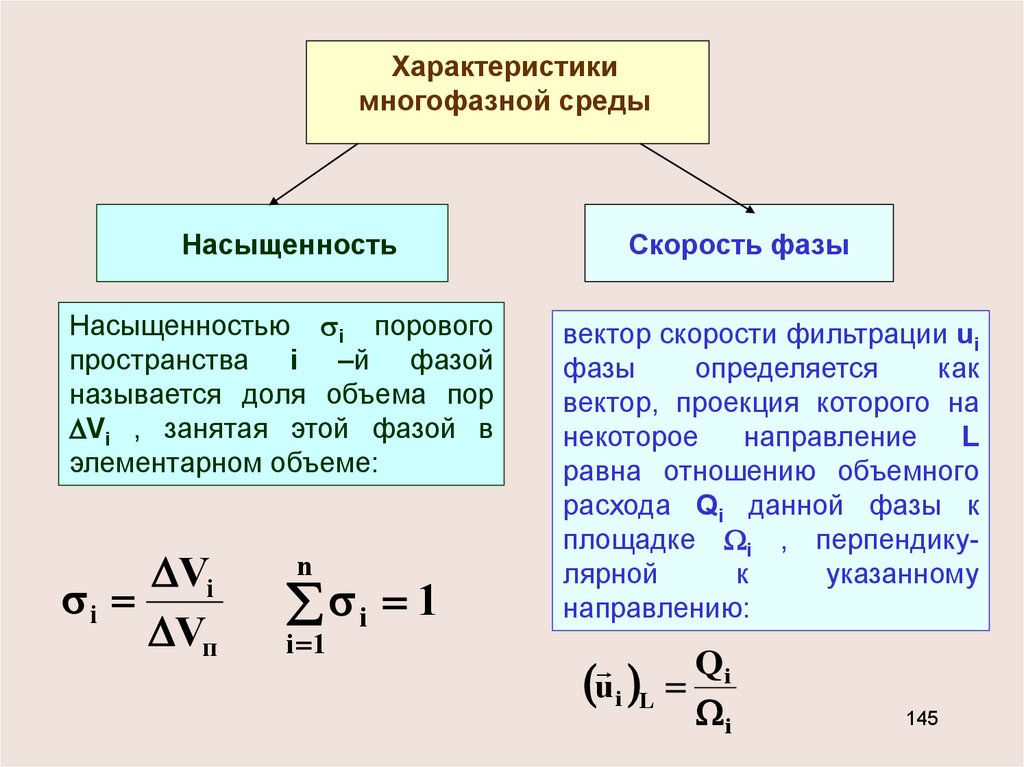
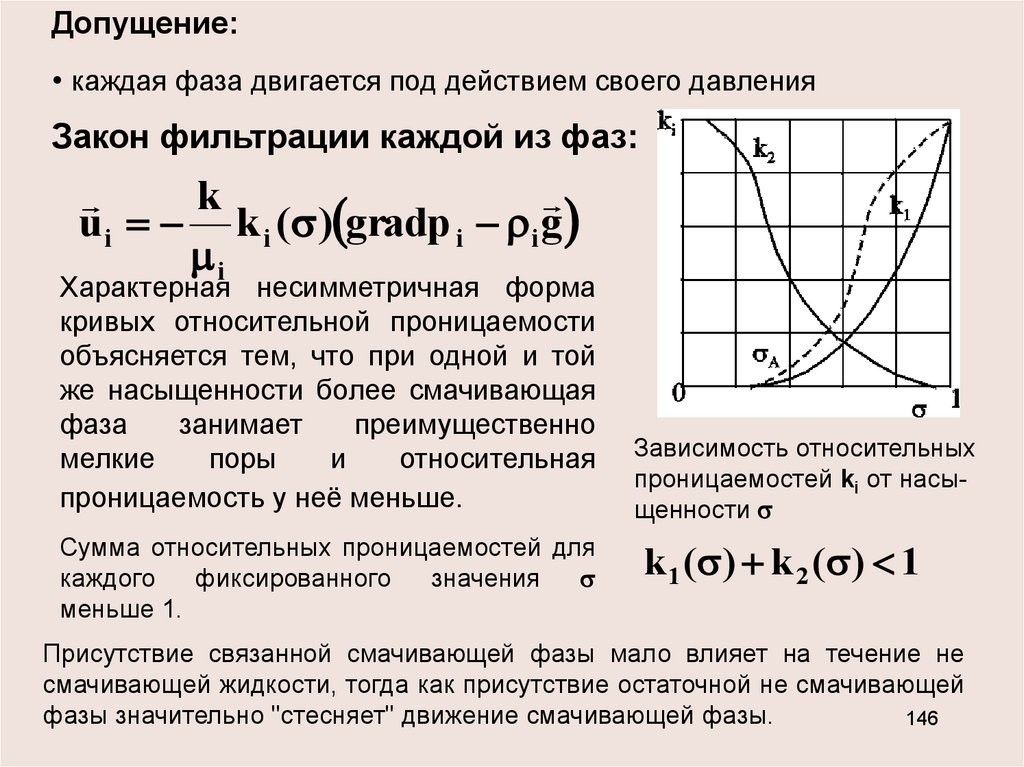
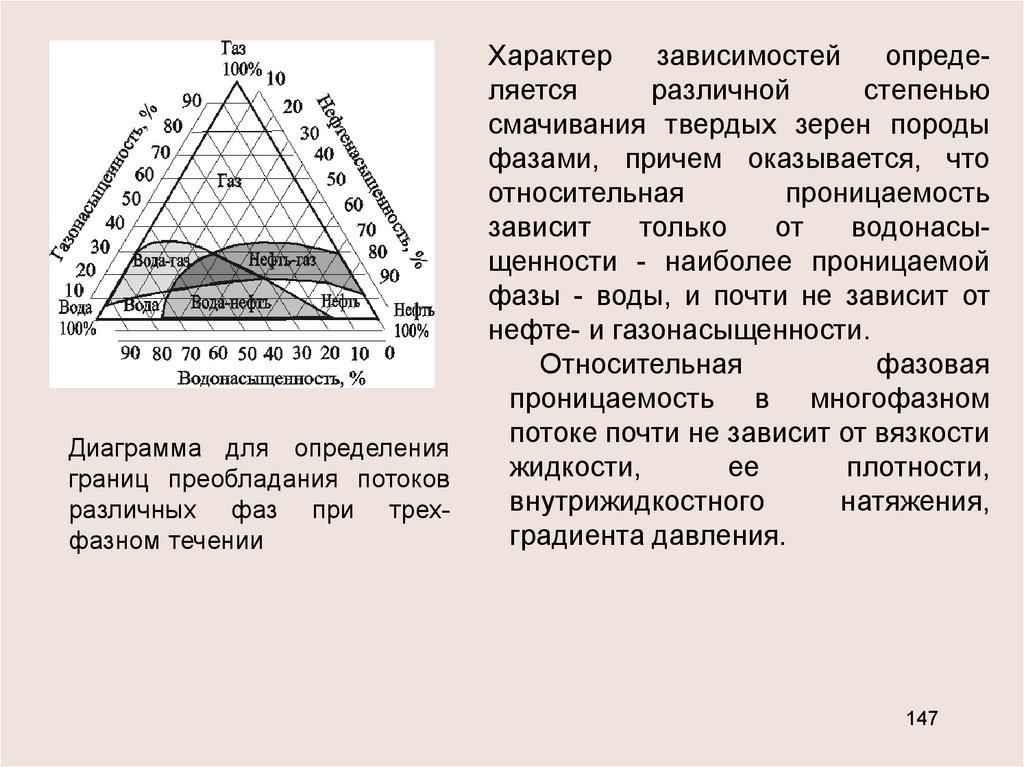






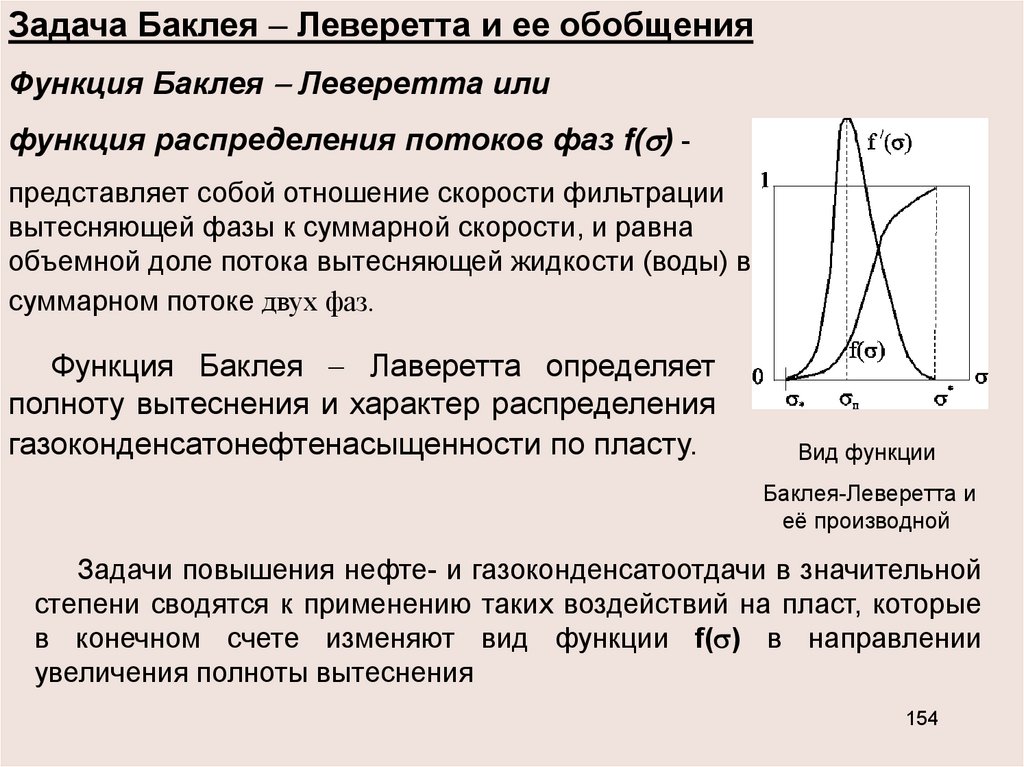
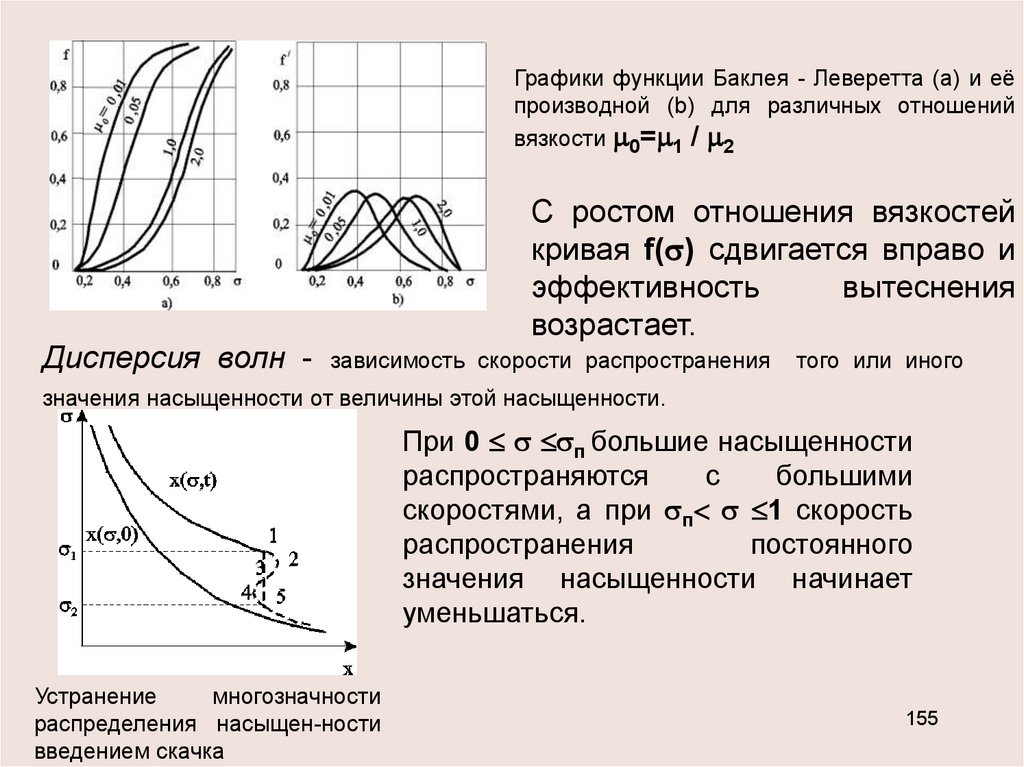
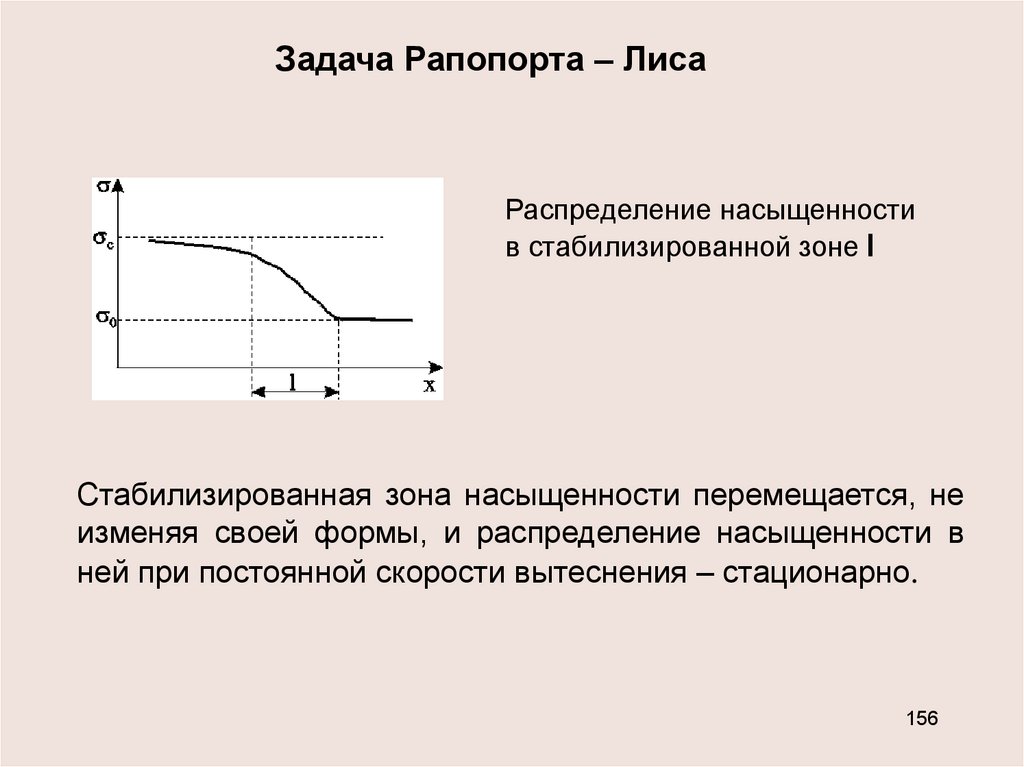

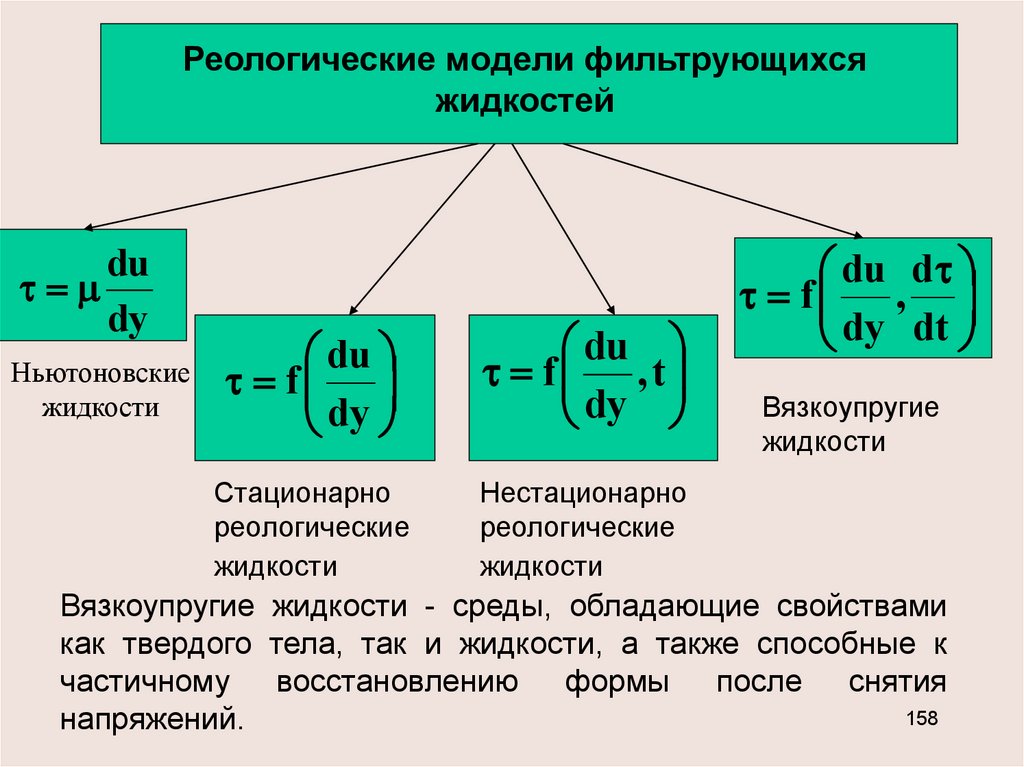
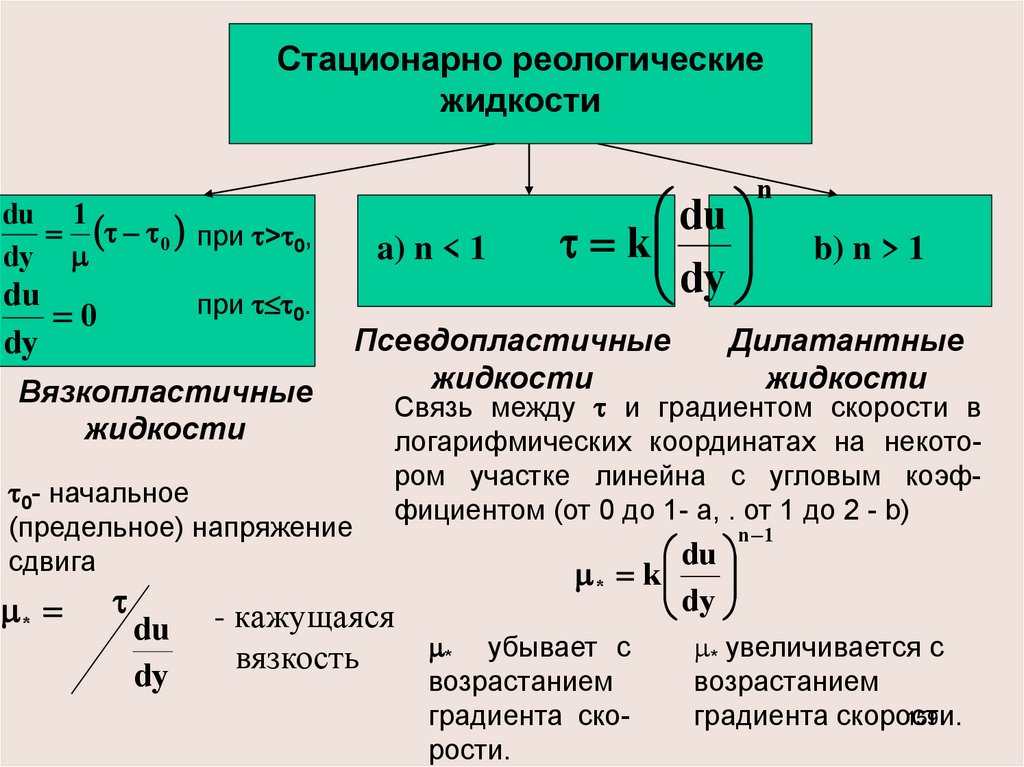
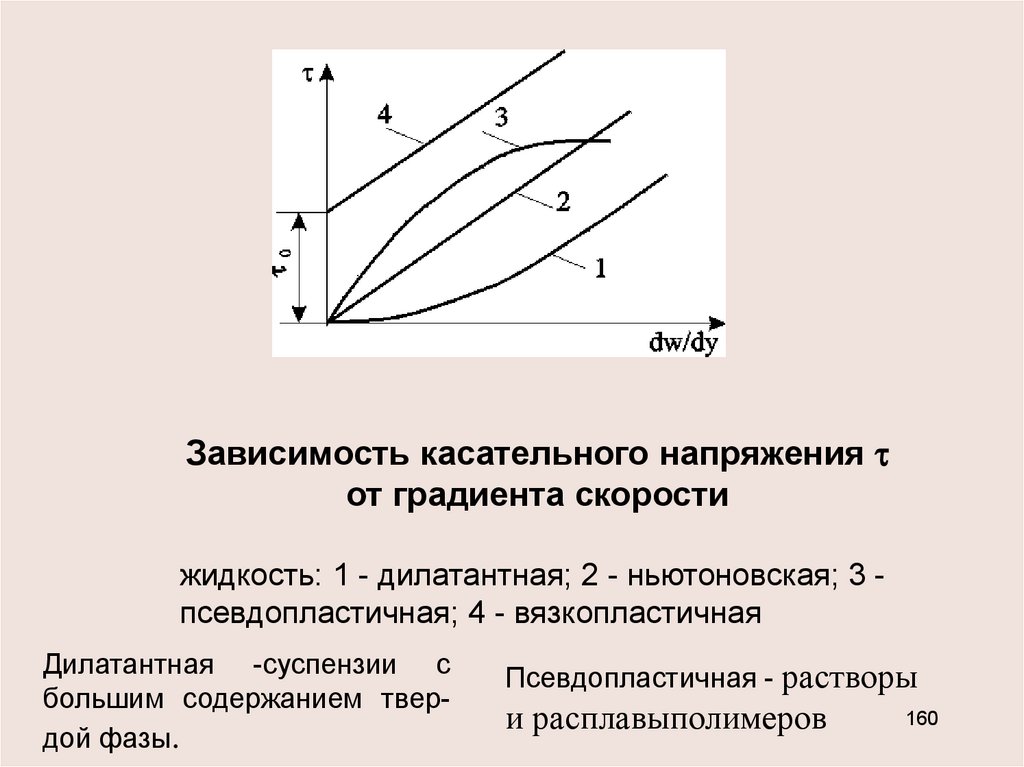
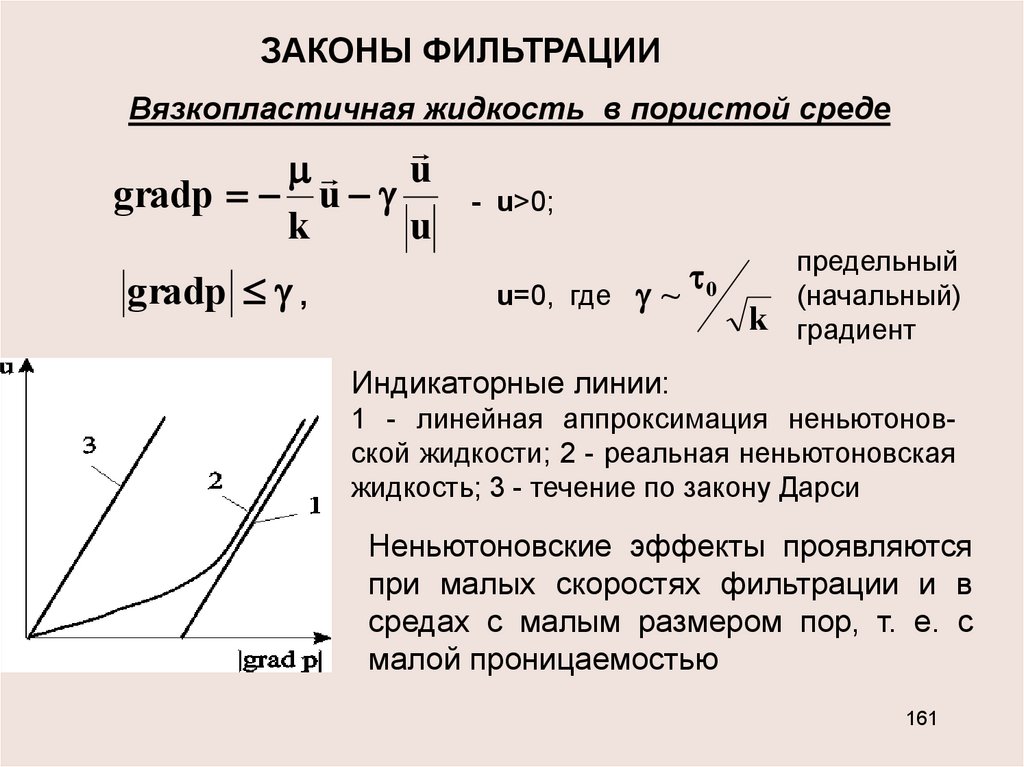



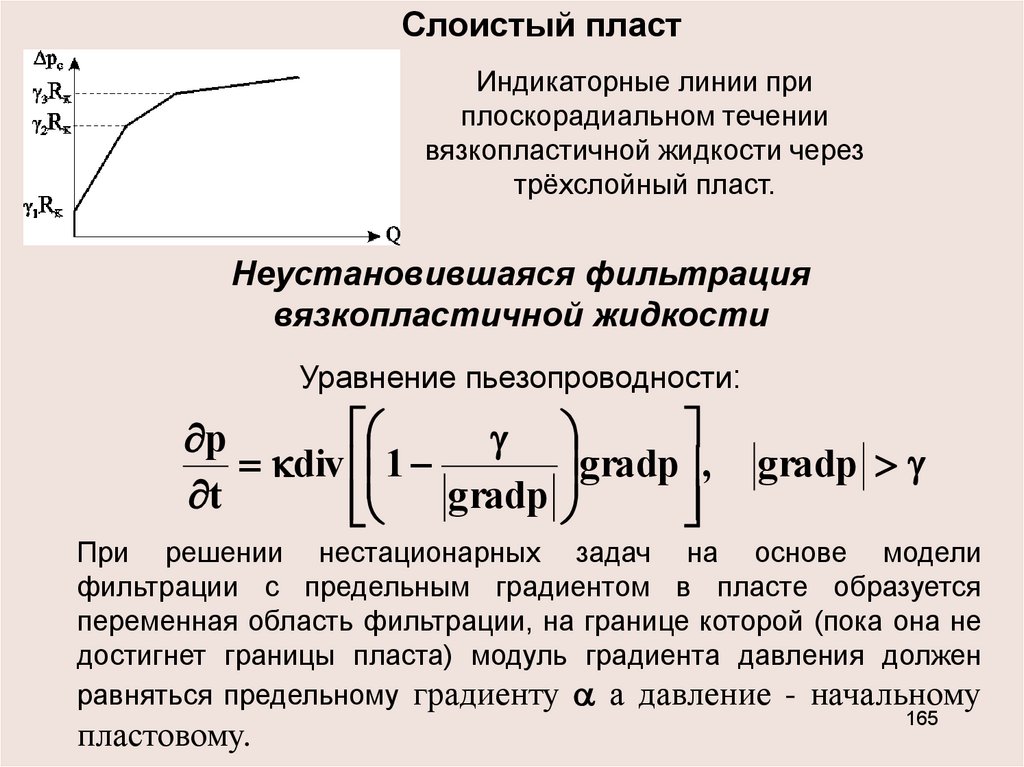
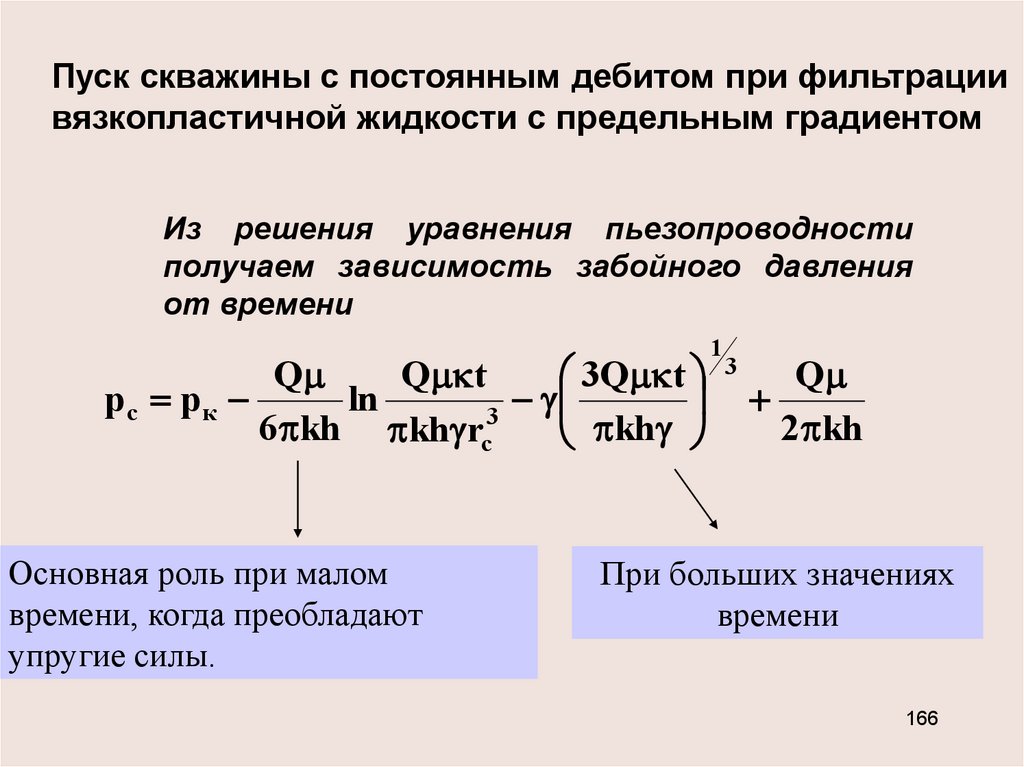

 Промышленность
Промышленность








