Вероятность случайного события. Примеры невозможных и достоверных случайных событий

1.

2.

1. Какие значения может принимать вероятность
случайного события?
2. Какие события называют достоверными? Чему равна
вероятность достоверных событий?
3. Какие события называют невозможными? Чему равна
вероятность невозможного события?
4. Приведите примеры невозможных и достоверных
случайных событий.

3.

Какие вы знаете способы для определения вероятностей?
В некоторых случаях вероятность события можно
установить, зная свойства самого события или
обстоятельства, в которых оно может наступить.
Например, при бросании монеты (если эта монета не
испорчена) естественно считать, что шансы на появление
орла и решки одинаковы.
Экспериментальный способ определения вероятности
основан на наблюдениях. Выше было сказано, что при
многократных повторениях опыта частоты случайных
событий оказываются близки к их вероятностям. Поэтому
если опыт можно повторять достаточно много раз, то
вероятность случайного события можно приближенно
найти, вычисляя его частоту.

4.

Как узнать вероятность события
Иногда мы можем установить вероятности событий
исходя из особенностей эксперимента. Например,
при бросании монеты разумно считать, что
шансы на появление орла и решки одинаковы, и
поэтому мы считаем, что вероятность выпадения
каждой стороны равна 1/2. Правильная игральная
кость симметрична, и поэтому вероятности
выпадения всех граней мы тоже полагаем одинаковыми, а потому равными 1/6.

5.

Но симметрия в случайном эксперименте имеет
место редко. Чаще приходится оценивать вероятности
событий экспериментально, опираясь на их частоты.
При многократных повторениях опыта частоты
случайных событий оказываются близки к их
вероятностям. Поэтому, если опыт можно повторять
много раз, то вероятность случайного события можно
приближённо найти, вычислив его частоту.
Вероятность часто оценивается при помощи
собранных данных: синоптики это делают на основе
данных о погоде, медики — на основе исследований,
инженеры – на основе экспериментов.

6.

В социологии и маркетинге для оценки вероятностей
используются опросы и анкетирования. Опрос
используется для получения надежных данных на
основе выборки.
Пример 9. В классе провели опрос «У кого в семье
живет собака?». Выборкой из всего множества
школьников здесь служит один класс.
Опрос показал, что из 32 учеников собаку дома
держат 7 человек. Значит, неизвестная вероятность
события «В случайно выбранной семье есть собака»
7
оценивается дробью .
32

7.

Нельзя утверждать, что эта оценка — точное
значение вероятности события «У школьника дома
есть собака». Такая оценка — случайная величина.
Она зависит от выборки и будет меняться от класса
к классу.

8.

На оценку вероятности исследуемого события
могут влиять могут различные факторы.
Например, если опрос проводили бы в деревне, то
оценка была бы выше: в деревне собак заводят не
только в качестве любимцев, но и для охраны. То
есть, оценка может зависеть от культурных
традиций местности и подобного.
Заметим, чем больше выборка, тем, скорее всего,
результат будет ближе к истинной вероятности.
Приведем пример.

9.

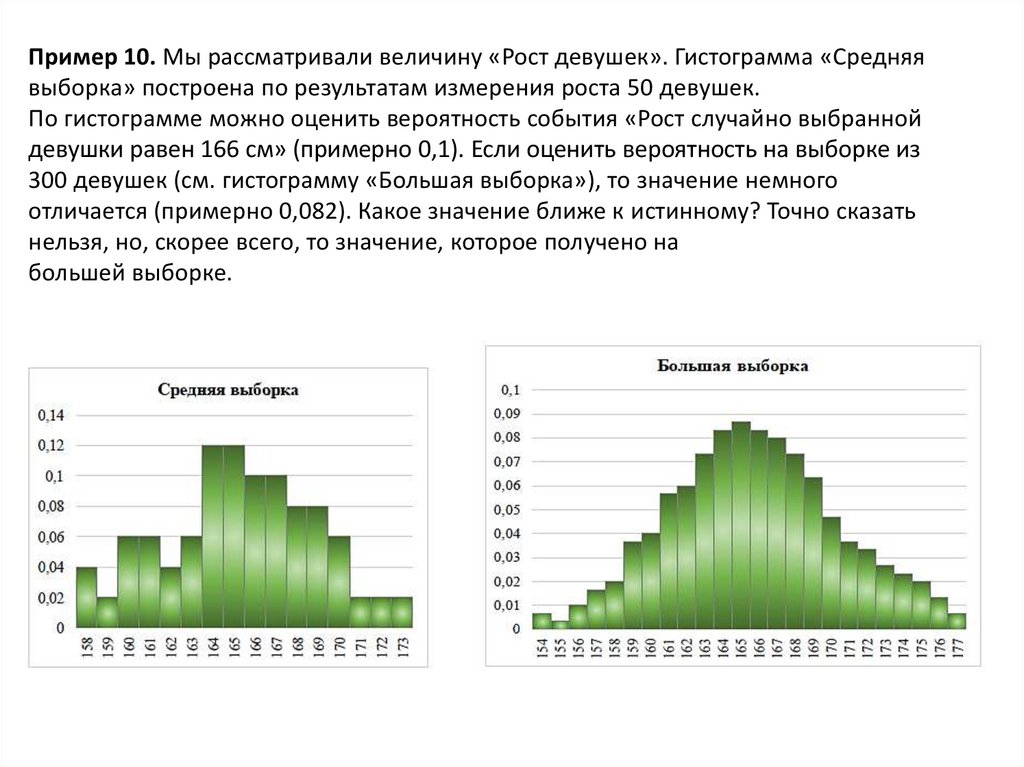
Пример 10. Мы рассматривали величину «Рост девушек». Гистограмма «Средняя
выборка» построена по результатам измерения роста 50 девушек.
По гистограмме можно оценить вероятность события «Рост случайно выбранной
девушки равен 166 см» (примерно 0,1). Если оценить вероятность на выборке из
300 девушек (см. гистограмму «Большая выборка»), то значение немного
отличается (примерно 0,082). Какое значение ближе к истинному? Точно сказать
нельзя, но, скорее всего, то значение, которое получено на
большей выборке.

10.

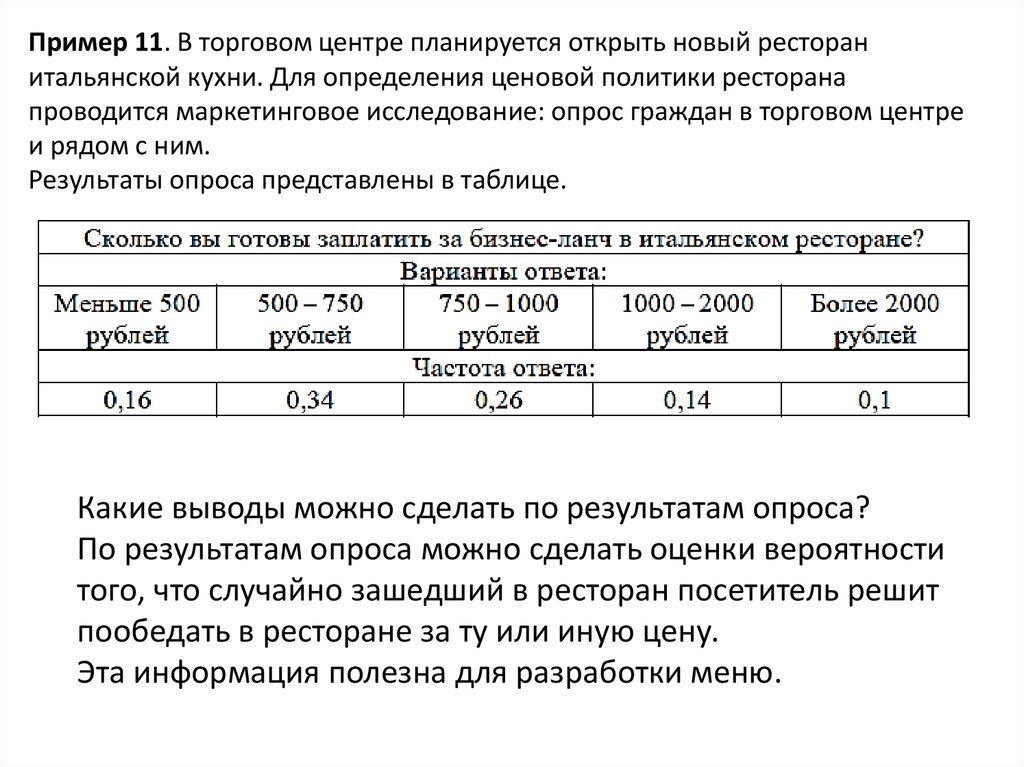
Пример 11. В торговом центре планируется открыть новый ресторан
итальянской кухни. Для определения ценовой политики ресторана
проводится маркетинговое исследование: опрос граждан в торговом центре
и рядом с ним.
Результаты опроса представлены в таблице.
Какие выводы можно сделать по результатам опроса?
По результатам опроса можно сделать оценки вероятности
того, что случайно зашедший в ресторан посетитель решит
пообедать в ресторане за ту или иную цену.
Эта информация полезна для разработки меню.

11.

Зачем нужно знать вероятность событий
Что может дать вероятность случайного события? Как эти знания можно
использовать?
Зная вероятность события, мы можем сказать, насколько часто это событие
будет происходить в жизни. Например, если какое-то событие имеет
вероятность 0,99, то в среднем его следует ожидать в 99 случаях из 100, т. е.
почти всякий раз. Напротив, если событие имеет вероятность 0,01, то
происходит оно редко, примерно в одном случае из ста. Зная вероятности,
мы можем планировать будущие действия. В некоторых профессиях важно
уметь оценивать вероятности, и чем точнее, тем лучше.
Метеорология
Пример 15. На сегодняшний день в Москве действует система СМСоповещений граждан о надвигающихся на город природных катаклизмах,
которые могут представлять угрозу жизни и здоровью граждан. Мы
периодически получаем сообщения от МЧС.
Синоптики изучают погодные условия, делают прогнозы, основываясь
на оценках вероятности того или иного погодного явления (скорость ветра,
град, гроза), и в зависимости от этого определяют уровень погодной
опасности.

12.

В зависимости от уровня погодной опасности и вероятности наступления
прогнозируемых явлений МЧС принимает решение об оповещении
граждан, а также о приведении служб и техники в готовность.
Синоптики в своей профессиональной деятельности оценивают
вероятность того или иного явления, а также следят за изменением этой
вероятности.
Например, если крупное кучевое облако с мощным вертикальным
развитием превращается в «наковальню» или «гриб» (то есть расширяются
с высотой), выбрасывая при этом опахала перистых и/или перисто-слоистых
облаков, — есть вероятность града. Причем вероятность града тем выше,
чем больше высота облака.

13.

Медицина
Пример 16. Прежде чем новое лекарство поступит в продажу,
производится тщательное изучение его безопасности, эффективности и
побочных эффектов.
Сначала испытания нового лекарства проводятся на отдельных тканях и
на лабораторных животных с целью оценки рисков, а уже потом
исследуется его действие на человеке. Необходимо оценить соотношение
рисков побочных действий с ожидаемой пользой.
Исследование действия препарата на человеке (клинические испытания)
проходит в несколько этапов. Сначала препарат принимает небольшая
группа добровольцев, и на основе собранных данных оценивается риск
для здоровья. Если риски минимальны, то испытания продолжаются на
большем числе пациентов. На основе собранных данных оценивается
вероятность лечебного эффекта и вероятность осложнений при приеме
лекарства. Затем составляются инструкции к препарату, понятные не
только исследователям, но и врачам, и пациентам.

14.

Пример 17. В августе 1945 года на японские города Хиросима и
Нагасаки были сброшены ядерные бомбы, что привело к ужасающим
разрушениям и жертвам. Примерно 200 000 людей сразу погибло от
взрыва и сильной радиации. Около половины из тех, кто выжил,
приняли участие в исследованиях на протяжении всей жизни. Медики
собрали статистику о заболеваниях у людей, получивших высокую
дозу радиации. Также оценивалась вероятность патологий у потомков
облучённых.
Например, в ходе исследования было установлено, что
злокачественные новообразования и генетические нарушения могут
возникать при любых дозах облучения. С увеличением дозы
радиации повышается не тяжесть этих болезней, а вероятность их
возникновения. Данные стали основой для определения безопасных
доз облучения для работников атомной отрасли. Также результаты
исследования широко использовались и используются медиками,
работающими с пострадавшими от аварий АЭС в Чернобыле и в
Фукусиме и от других аварий с радиационными выбросами.

15.

Инженерная деятельность
Любая новая техника подробно изучается. Важная инженерная задача —
создание безопасных технологий и техники.
Пример 18. На атомных электростанциях собирается статистика
работы реактора. Это нужно для изучения поведения реактора в
случае сбоя в его работе и для подготовки персонала. Определяется
ядерная безопасность реактора — свойство реакторной установки с
высокой вероятностью предотвращать ядерную аварию. В процессе
испытаний исследуется поведение реактора и вспомогательных систем на
разных мощностях, работоспособность аварийных систем и так далее.
Специалисты по безопасности делают точный прогноз и оценивают
вероятности возможных сбоев, пишут инструкции на случай той или иной
чрезвычайной ситуации.
История атомной энергетики знает печальные последствия недооценки
вероятности аварий.

16.

В 1986 году на 25 апреля была запланирована остановка 4-го
энергоблока Чернобыльской АЭС для ремонта. Во время
таких остановок обычно проводятся испытания
оборудования.
26 апреля 1986 года примерно в 1:24 ночи на энергоблоке
произошёл взрыв, который разрушил реактор. Причина
была в том, что персонал станции не знал, что из-за
изменения режима реактора резко возросла вероятность
взрыва. Последствия известны всему миру — произошла
крупнейшая и истории атомной энергетики катастрофа.
Соблюдения правил безопасности требует и более
привычная нам техника. С повышением скоростей и
мощностей автомобилей растут требования
к их исправности.

17.

Пример 19. Перед массовым выпуском новый автомобиль испытывают на
разных скоростях и на разных дорогах, в дождь, в снег и в гололёд, при различном направлении и скорости ветра. В ходе испытаний оцениваются
скорость, экономичность, торможение, управляемость и устойчивость,
плавность хода, проходимость, шум и вибрация, эргономические свойства,
надежность, пассивная безопасность и др. Исследуется вероятность отказа
тормозной системы, ремней и подушек безопасности.
К сожалению, иногда конструкторы совершают ошибки. Если выявляется
опасный недостаток в конструкции, то компания отзывает машины для
устранения дефекта. Часто отзыв партии осуществляется на основе оценки
вероятности отказа какой-либо системы. Если она высокая, то партию
автомобилей отзывают.
Например, компания Ford в 2018 г. отозвала 2 млн. автомобилей после
многочисленных жалоб на самовозгорание в системе натяжения ремней
безопасности.

18.

Пример 20. Испытания самолетов гражданской авиации
регламентируются специальным стандартом.
Эксплуатационным испытаниям подвергаются все новые, а
также модифицированные самолеты.
Сейчас в Иркутске готовится к серийному выпуску новый
Российский самолет МС-21. Первый полёт состоялся 28 мая 2017
года, и испытания продолжаются до сих пор. Программа
испытаний включает 1600 полётов, вовремя которых
оценивается вероятность отказа каждой системы — от
двигателя до чайника, в котором будут кипятить воду в полёте.
Только в августе 2019 года МС-21, наконец, появился на
авиасалоне МАКС. В рамках программы импортозамещения
этот самолет оснастили отечественными двигателями, и с
августа 2021 проводятся лётные испытания, в ходе которых идет
сбор статистики по нагруженности планера во время взлётов и
посадок.

19.

Страхование
Страхование — способ возмещения ущерба имуществу или
здоровью людей. Страховая деятельность полностью основана
на теории вероятностей.
Страхователь, покупая страховой полис, платит небольшой
взнос страховщику, а страховщик обязуется возместить ущерб
(пожар, кража, ДТП, болезнь и т.п.). Стоимость полиса во
много раз ниже суммы ущерба. При расчёте стоимости полиса
оцениваются вероятности разных неприятных событий
и вычисляется средняя выплата на один купленный полис.

20.

Пример 21. Каждый автовладелец в России должен
иметь страховой полис ОСАГО (обязательное
страхование автогражданской ответственности). В
случае ДТП по вине владельца полиса страховая
компания оплачивает нанесённый им материальный
ущерб.
Статистика ДТП постоянно пополняется, меняются
цены на автомобили, поэтому полис ОСАГО часто
переоценивается.

21.

Пример 22. Страховые компании предлагают
медицинское страхование:
оплату стоимости лечения и — иногда — ущерба,
понесенного из-за болезни.
В России действует программа ОМС (обязательное
медицинское страхование). Кроме того, клиент
может заключить договор о добровольном медицинском страховании (ДМС).
Любое страхование требует расчетов и оценок.
Поэтому в страховых компаниях работают
специальные аналитики — математики,
специализирующиеся на теории вероятностей в
страховании.

22.

Выводы
О случайном событии чаще всего нельзя сказать заранее,
произойдёт оно или нет. Но можно говорить о том, насколько
оно правдоподобно. Правдоподобие события измеряют с
помощью вероятностей. Вероятность события выражается
числом от 0 до 1. Чем больше шансов у события, тем выше
его вероятность.
Не существует единого и универсального способа определить
вероятности событий.
1. Иногда вероятности элементарных событий назначают из
соображений симметрии (пример: вероятности орла и решки
при бросании монеты).
2. Иногда вероятности можно найти приближенно с помощью
многократных экспериментов (пример: вероятность поломки
телевизора определенной модели в течение гарантийного
срока). Если в некотором опыте наблюдается событие А, и этот
опыт повторяется много раз, то частота события А постепенно
приближается к вероятности события А.

23.

Монета и игральная кость — простейшие
вероятностные модели. С их помощью удобно
учиться, но не только. С помощью таких простых
моделей как кость или монета можно моделировать
гораздо более сложные и ответственные случайные
опыты.
На основе статистических данных можно оценивать
вероятность события. Точность оценки зависит от
качества и объема выборки. Оценка вероятностей
событий часто служит основой для принятия
решений.