Похожие презентации:
Двойственный симплекс-метод
1.
Двойственный симплекс-методC ( х) 5 x1 7 x 2 min
4 x1 3 x 2 21
x1 3
x2 2
x1 , x 2 0
Приведем к каноническому виду, введя дополнительные
переменные х3, х4, х5 0.
2.
C1 ( х) 5 x1 7 x2 max4 x1 3 x2 x3 21
x x 3
1 4
х 2 х5 2
x j 0,
j 1,5
Умножим второе и третье структурное ограничение на (-1)
C1 ( х) 5 x1 7 x 2 max
4 x1 3 x 2 x3 21
x1 x 4 3
x 2 x5 2
x j 0,
j 1,5
3.
Векторы А3, А4, А5 образуют единичный базис этой ЗЛП.Частным решением будет вектор х0 = (0; 0; 21; -3; -2).
Опр. Решение системы линейных уравнений
x 0 ( x10 , x 20 ,..., x n0 ) , соответствующее базису А ,
называется псевдопланом или почти
допустимым базисным решением (ПДБР), если
все двойственные оценки неотрицательны
( j , j 1, n), а среди координат плана существует,
по крайней мере, одна отрицательная координата
(x0k < 0, k ).
Здесь ik : xik 0,
k 1, l , l m .
4.
Чаще всего псевдоплан появляется в задачах, в которых:1. Ограничения имеют вид Ах b.
2. Коэффициенты целевой функции сj 0, j 1, n
и при этом C(х) min.
3. В ЗЛП вводится существенное или активное
ограничение, т.е. такое ограничение, которое изменяет
оптимальный план в первоначально заданном
множестве допустимых планов.
5.
Теорема. Признак оптимальности псевдоплана.Пусть х* = (х*1 ,…, х*n) – псевдоплан, в котором
x *j 0,
j 1, n , тогда х* – оптимальный план.
Доказательство. Так как х* псевдоплан, то ему
соответствует некоторый базис. Поскольку по условию
теоремы x *j 0,
j 1, n , то х* – БДП.
Из определения псевдоплана следует, что j 0,
При
этом
попадаем
в
условия
теоремы
j 1, n.
«Признак
оптимальности БДП». Таким образом, х* – оптимальный
план.
6.
Алгоритм двойственного симплекс-метода(с, х) max
Aх b
х 0
(1)
Мы имеем систему ограничений вида:
xk akj x j xk 0 , k
(2)
j
В (2) все координаты x0k не определены по знаку. При этом в
ЗЛП (2) все оценки
j 0,
j 1, n
.
7.
Правило 1. Определение номера вектора, выводимого избазиса.
Из базиса выводится вектор Ar , у которого номер r
определяется из соотношения:
min xk 0 xr 0 0 или
k
max xk 0 xr 0
xk 0 0
8.
Правило 2. Определение номера вектора, вводимого вбазис.
Номер вектора s, вводимого в базис, выбирается из
отношений двойственных оценок к отрицательным
элементам r-ой строки симплекс-таблицы:
j
min
a rj 0
a
rj
s
a
rs
или
Ведущим элементом будет
j
s
max
0
a rj 0 a
a
rj
rs
ars
.
9.
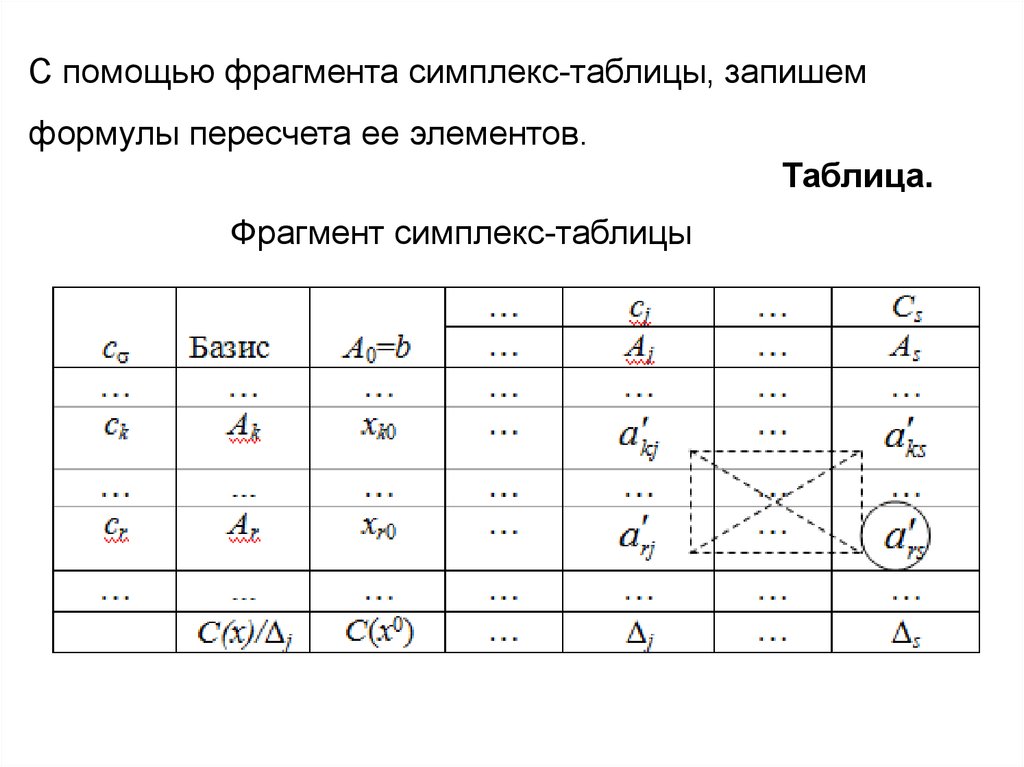
С помощью фрагмента симплекс-таблицы, запишемформулы пересчета ее элементов.
Таблица.
Фрагмент симплекс-таблицы
10.
Компоненты нового псевдоплана определяются согласно (3).x kнов
xr 0
а ks ,
xk 0
а rs
xr 0
,
а rs
0,
k s,
k
(3)
k s
k
Другие элементы симплексной таблицы вычисляются по
формулам:
а rj
нов
а ks ,
а kj а kj
а rs
а rj
нов
а kj
,
а rs
нов
а
rs
k s,
k s,
j 1, n,
j 1, n
1, r s
0, r s
j s
(4)
11.
Двойственные оценки:нов
j
j
аrj
аrs
s
(5)
Значение целевой функции на новом псевдоплане:
C(х
нов
хr 0
) C(х )
s
а rs
0
(6)
12.
Теорема 10.Применение правил 1 и 2, а также формул (3) (6)
обеспечивает:
1) переход к новому псевдоплану, т. е. гарантируется
а) j 0,
j 1, n
б) новый псевдоплан хнов есть базисный план.
2) Значение целевой функции на новом псевдоплане не
больше, чем значение целевой функции на предыдущем
псевдоплане, т.е. С(хнов) С(х0).
13.
П р и м е р 15.Приведем ЗЛП к каноническому виду
Базисный план х0 = (0; 0; 0; -16; -4) есть псевдоплан
14.
Строим симплекс-таблицу и решаем задачу.Получен оптимальный план х* = (0; 0; 8; 0; 44)
Значение целевой функции C1(х*) = -8
Значение целевой функции исходной задачи C(х*) = 8.
15.
Признак отсутствия допустимых плановТеорема. Признак неразрешимости ЗЛП в двойственном
симплекс-методе.
Пусть в ЗЛП (1) имеется псевдоплан х* = (x1*, …, xr*, …, xn*)
такой, что r-я координата меньше нуля, а все элементы r-й
строки симплексной таблицы неотрицательны, тогда ЗЛП
неразрешима.
Более короткая формулировка теоремы:
Если существует псевдоплан х* = (x1*,…, xr*,…, xn*) такой,
что xr * < 0, а элементы а rj 0, j =1, n , то мн-во D = .
16.
П р и м е р.Выполнив эквивалентные преобразования получаем:
Составим симплексную таблицу:
17.
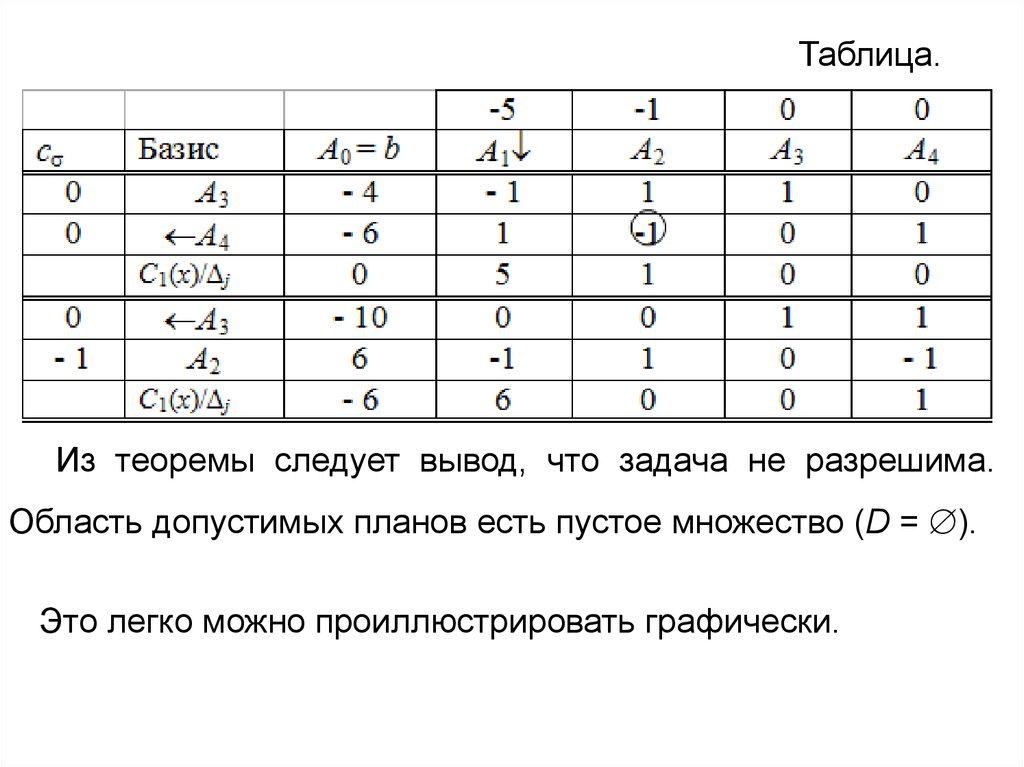
Таблица.Из теоремы следует вывод, что задача не разрешима.
Область допустимых планов есть пустое множество (D = ).
Это легко можно проиллюстрировать графически.
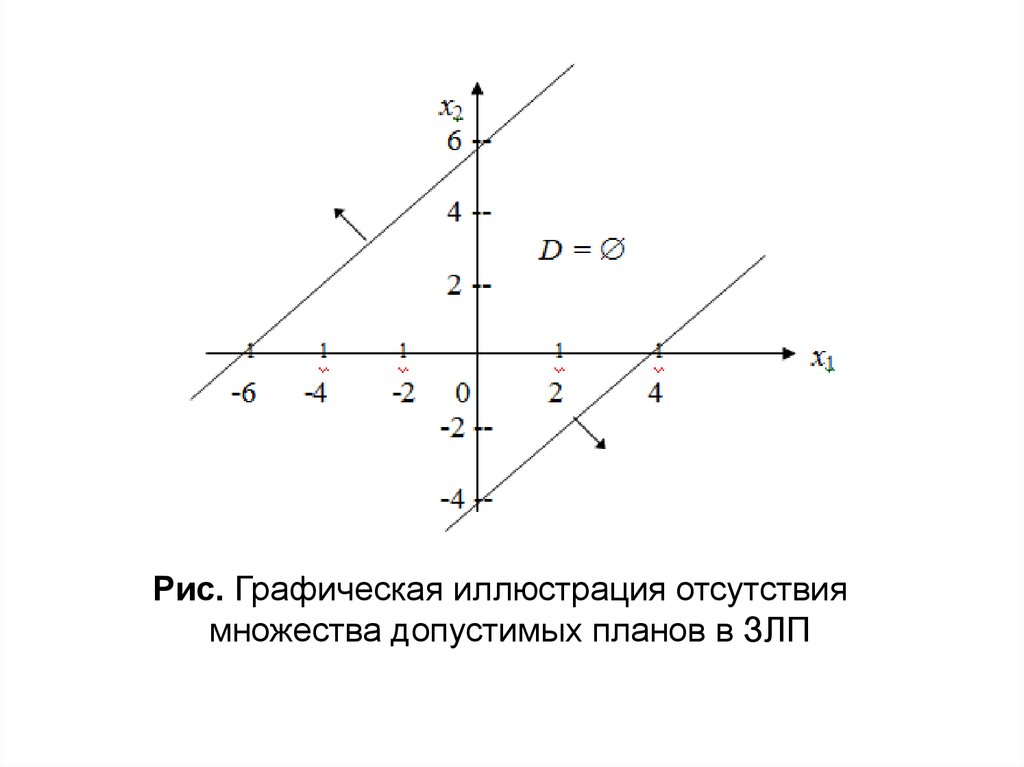
18.
Рис. Графическая иллюстрация отсутствиямножества допустимых планов в ЗЛП
19.
Решение ЗЛП с дополнительным активным ограничениемДопустим, что ЗЛП (1) имеет оптимальный план
x * ( x1* ,..., x n* )
Известен носитель оптимального плана
* i1 , i2 ,..., im и *j 0,
j 1, n
Последней итерации симплексной таблицы соответствует
система уравнений
xk akj x j xk 0 , k *
j
Координаты оптимального плана х*
*
xk 0 , k
*
xk
0 , k
(7)
20.
Добавим к исходной ЗЛП (1) дополнительное активное или,как еще говорят, существенное ограничение вида:
n
a
j 1
m 1, j
x j bm 1
(8)
Введем в неравенство (8) дополнительную переменную
x n+1 0.
n
a
j 1
a
k *
m 1, k
m 1, j
x j xn 1 bm 1
(9)
xk am 1, j x j xn 1 bm 1
j
(10)
21.
Выразим xk из (7) и подставим в уравнение(10). Получим уравнение (11).
a
k *
m 1,k
(xk 0 akj x j ) am 1, j x j xn 1 bm 1
j
j
(11)
22.
Выделим и сгруппируем свободные переменные, апостоянные члены перенесем в правую часть уравнения (11):
xn 1 (am 1, j
j
a
m 1,k
akj ) x j bm 1
k *
a
m 1,k
xk 0
(12)
k *
Обозначим xm 1, 0 bm 1
a
m 1, k
xk 0 , тогда дополнительная
k *
переменная xn+1 = xm+1,0. Запишем (12) в (m+1) строку
симплекс-таблицы. Появляется новый единичный
базисный вектор An+1.
За счет дополнительного ограничения (12) получили новую
ЗЛП, в которой имеется псевдоплан
x нов
x*
x
m 1, 0
23.
Действительно, n новых двойственных оценок равныпрежним двойственным оценкам, а оценка n+1 = 0, как
оценка базисного вектора An+1. Кроме того, xm+1,0 0,
так как
bm 1
a
k
*
m 1,k
xk 0
в силу предположения, что
дополнительное ограничение активное.
Имея псевдоплан, можно продолжать решение ЗЛП
двойственным симплекс-методом.
24.
П р и м е р 19.Предприятие изготавливает для постоянного заказчика
изделие А основной номенклатуры и изделие В
второстепенной номенклатуры. Издержки на производство
одного изделия А равны 5 ден. ед., а изделия В – 1 ден. ед.
Заказчик требует как минимум на четыре единицы больше
изделия А , чем изделия В. Производство одного изделия А
дает единицу токсичных отходов, а изделия В – две
единицы отходов. Общее количество токсичных отходов не
должно превышать 12 единиц. Необходимо так
организовать производство, чтобы минимизировать
издержки.
25.
(l1) и (l2) обозначения прямых линий, ограничивающихсоответствующие полуплоскости.
26.
Решение производственной задачи27.
Получен оптимальный план х* = (4; 0; 8; 0)Издержки составят С(х*) = 20 ден. ед.
Теперь обстоятельства изменились. Заказчик потребовал
изготовить не менее 6 штук изделий А. Появляется новое
активное ограничение х1 6 (обозначим соответствующую
прямую l3).
Вводим дополнительную переменную х5 0
28.
Выразим х1 из второго уравнения и подставимв третье уравнение. Тогда
Применяя алгоритм двойственного симплекс-
метода, получаем оптимальный план
х1* = (6; 0; 6; 2; 0), С(х1*) = 30 ден. ед.
Геометрическая иллюстрация решения данной
задачи показана на рис.


























 Математика
Математика








