Функции нескольких переменных. Тема 7.5. Экстремум функции двух переменных

1.

2.

7. ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ
7.1 ФНП и способы её задания
7.2. Предел и непрерывность
7.3. Частные производные 1-го порядка
7.4. Частные и смешанные производные различных порядков
7.5 Экстремум функции двух переменных
7.6 Полное приращение и полный дифференциал
7.7 Производная по направлению
7.8 Градиент
7.9 Касательная плоскость и нормаль к поверхности

3.

7.5 ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Точка М0(х0 ,у0) называется точкой локального максимума функции z=f(x,y),
если существует такая окрестность этой точки, что для любой точки М(x,y)
из этой окрестности выполняется неравенство: f ( M ) f ( M ).
0
или
Точка М0(х0 ,у0) называется точкой локального максимума функции z=f(x,y),
если
U ( M 0 ) : M x, y U ( M 0 ) f ( M 0 ) f ( M ).
M 0 точка максимума
Значение функции в точке
локального максимума
называется локальным
максимумом функции.
f ( M 0 ) максимум функции

4.

7.5 ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Точка М0(х0 ,у0) называется точкой локального минимума функции z=f(x,y),
если существует такая окрестность этой точки, что для любой точки М(x,y)
из этой окрестности выполняется неравенство: f ( M ) f ( M ).
0
или
Точка М0(х0 ,у0) называется точкой локального минимума функции z=f(x,y),
если
U ( M 0 ) : M x, y U ( M 0 ) f ( M 0 ) f ( M ).
M 0 точка минимума
Значение функции в точке
локального минимума
называется локальным
минимумом функции.
f ( M 0 ) минимум функции

5.

7.5 ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Понятие «экстремум» является обобщающим,
это или локальный максимум, или локальный минимум.
Замечания
1) Слово «локальный» можно опускать, не забывая, что речь идёт
о достаточно малой окрестности точки.
2) Функция может иметь экстремум только во внутренних точках
области определения.
Теорема. (необходимое условие существования экстремума)
Пусть функция z=f(x,y) дифференцируема в точке М0(х0 ,у0) и имеет в ней
экстремум, тогда частные производные 1-го порядка в этой точке равны 0.
Точка М0(х0 ,у0), в которой частные производные 1-го порядка равны 0,
называется стационарной точкой.

6.

7.5 ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Замечание
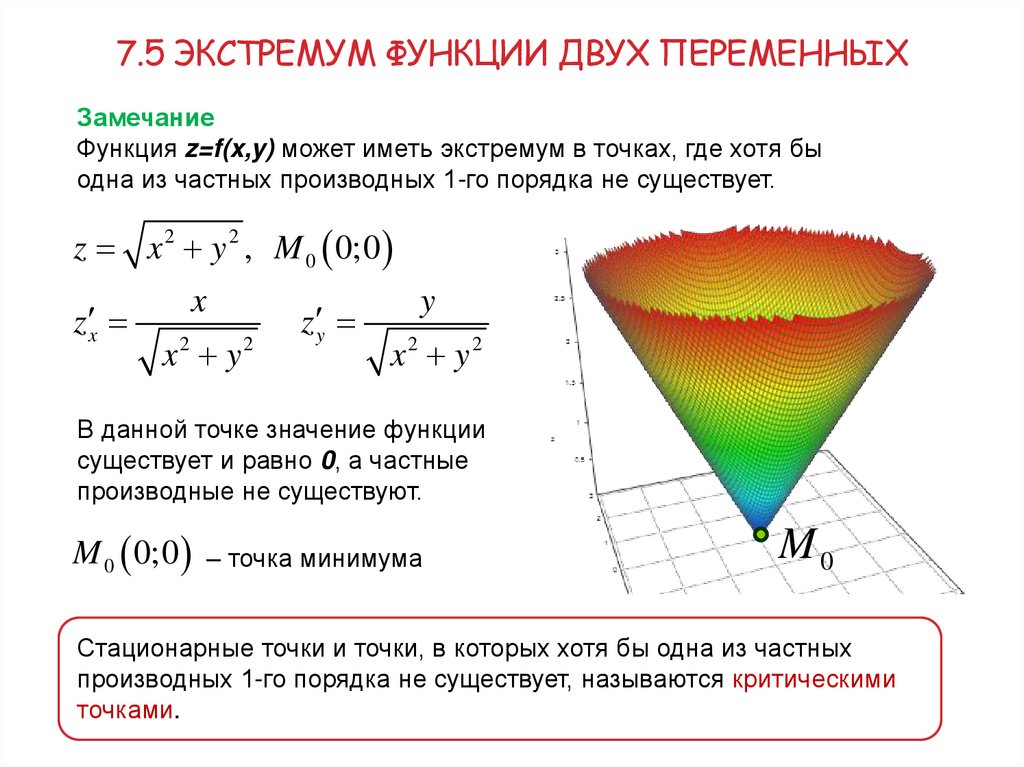
Функция z=f(x,y) может иметь экстремум в точках, где хотя бы
одна из частных производных 1-го порядка не существует.
z x 2 y 2 , M 0 0;0
z x
x
x y
2
2
z y
y
x2 y 2
В данной точке значение функции
существует и равно 0, а частные
производные не существуют.
M 0 0;0 – точка минимума
M0
Стационарные точки и точки, в которых хотя бы одна из частных
производных 1-го порядка не существует, называются критическими
точками.

7.

7.5 ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Теорема. (достаточное условие существования экстремума)
(Признак Сильвестра)
Пусть в критической точке М0(х0 ,у0) и её некоторой окрестности функция
z=f(x,y) имеет все производные 2-го порядка.
Пусть
A B
D M0
AC B 2 , где
B C
A z xx M 0 , B z xy M 0 , C z yy M 0 .
M 0 0, то в точке М (х ,у ) экстремума нет.
2) если D M 0 0, то в точке М (х ,у ) экстремум есть, причём:
Тогда: 1) если D
0
0
0
0
0
0
а) если А>0, то это локальный минимум,
б) если А<0, то это локальный максимум.

8.

7.5 ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Схема исследования функции z=f(x,y) на экстремум
1) Найти частные производные 1-го порядка.
z x 0
2) Решить систему уравнений
z y 0
3) Обозначить стационарные точки M 1 x1; y1 , M 2 x2 ; y2 , M 3 x3 ; y3 ...
4) Найти все производные 2-го порядка.
5) Для каждой стационарной точки вычислить А, В, С, D.
6) Сделать выводы по признаку Сильвестра.
7) Найти экстремум.

9.

7.5 ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Пример
Исследовать функцию
z 4 x 2 y 24 xy y 2 32 y 6 на экстремум.
z x 4 y 2 x 24 y 1 0 8 xy 24 y
z y 4 x 2 1 24 x 1 2 y 32 0 4 x 2 24 x 2 y 32
8 y x 3 0
8 xy 24 y 0
2
2
4 x 24 x 2 y 32 0
2 x 12 x y 16 0
8 y x 3 0
y 0 или x 3
y 0
2
2 x 12 x y 16 0
x 3
2
2 x 12 x y 16 0

10.

7.5 ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Пример
y 0
2
2 x 12 x y 16 0
2 x 2 12 x 16 0
x2 6 x 8 0
x 2 или x 4
2 3 12 3 y 16 0
2
x 3
2
2 x 12 x y 16 0
Получили три стационарные точки:
z xx 8 xy 24 y x 8 y
z 8 xy 24 y 8 x 24
xy
y
18 36 y 16 0
y 2 0
y 2
M 1 2;0 , M 2 4;0 , M 3 3;2 .
z yy 4 x 2 24 x 2 y 32 2
y

11.

7.5 ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Пример
A z xx 8 y; B z xy 8 x 24; C z yy 2
Найдём для каждой стационарной точки А, В, С, D и сделаем выводы:
M 1 2;0
A 2;0 0; B 2;0 8 2 24 8; C 2;0 2
0 8
D 2;0
0 64 64 0 экстремума нет
8 2
M 2 4;0
A 4;0 0; B 4;0 8 4 24 8; C 4;0 2
0 8
D 4;0
0 64 64 0 экстремума нет
8 2

12.

7.5 ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Пример
M 3 3;2
A 3;2 16; B 3;2 8 3 24 0; C 3;2 2
16 0
D 3;2
32 0 32 0 экстремум есть
0 2
A 3;2 16 0 в точке М 3 локальный минимум
Найдём этот минимум (экстремум):
zmin z 3;2 4 3 2 24 3 2 22 32 2 6 10
2

13.

7.5 ЭКСТРЕМУМ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
z 4 x 2 y 24 xy y 2 32 y 6

14.

7.6 ПОЛНОЕ ПРИРАЩЕНИЕ И ПОЛНЫЙ
ДИФФЕРЕНЦИАЛ
Полное приращение функции z=f(х,у) в точке M(x;y) имеет вид
z f ( x x, y y ) f ( x, y )
Функция z=f(х,у) называется дифференцируемой в точке M(x;y),
если её полное приращение в этой точке можно представить в виде:
z A( x; y ) x B ( x; y ) y x y
где и – бесконечно малые величины при
x 0 и y 0.
Замечание
A( x; y ) x B( x; y ) y
– главная часть полного
приращения функции.

15.

7.6 ПОЛНОЕ ПРИРАЩЕНИЕ И ПОЛНЫЙ
ДИФФЕРЕНЦИАЛ
Теорема (необходимое условие дифференцируемости)
Если функция z=f(х,у) дифференцируема в точке M(x;y), то
1) Она непрерывна в точке M(x;y).
2) Существуют частные производные первого порядка, причём
z x M A( x; y ) и z y M B ( x; y ).
Теорема (достаточное условие дифференцируемости)
Если частные производные первого порядка функции z=f(х,у)
существуют в некоторой окрестности точки M(x;y)
и непрерывны в самой точке M(x;y),
то функция z=f(х,у) дифференцируема в этой точке.

16.

7.6 ПОЛНОЕ ПРИРАЩЕНИЕ И ПОЛНЫЙ
ДИФФЕРЕНЦИАЛ
Главная часть полного приращения функции z=f(х,у) в точке M(x;y)
называется дифференциалом, т.е.
dz M z x M x z y M y
1
Пусть
z f ( x, y ) x dz 1 x 0 y
dx x
2
Пусть
z f ( x, y ) y dz 0 x 1 y
dy y
Тогда
dz z x dx z y dy
Для функции u=f(х,у,z)
du u x dx u y dy u z dz
Примеры
Найти дифференциалы функций (для функции u в точке M(1; 3; -2)).
z tg x y sin 2 y 15 y ;
3
2
x
y
u
2 2.
yz x z

17.

7.6 ПОЛНОЕ ПРИРАЩЕНИЕ И ПОЛНЫЙ
ДИФФЕРЕНЦИАЛ
Примеры
Найти дифференциал функции
1) z tg x3 y sin 2 y 2 15 y .
3x 2 y
z x
cos 2 x3 y
x3
2
z y
4
y
15
cos
2
y
15 y
2
3
cos x y
3x 2 y
x3
2
dz
dx
4 y 15 cos 2 y 15 y dy
2
3
2
3
cos x y
cos x y

18.

7.6 ПОЛНОЕ ПРИРАЩЕНИЕ И ПОЛНЫЙ
ДИФФЕРЕНЦИАЛ
Примеры
Найти дифференциал функции
1
2 xy
u x
yz x 2 z 2 2
u y
x
1
2 2
2
y z x z
x
2 yz
u z 2
yz x 2 z 2 2
2) u
x
y
2 2 в точке M (1;3; 2).
yz x z
1 6
61
u x (1;3; 2)
6 25
150
u y (1;3; 2)
1 1 23
18 5 90
1 12 119
u z (1;3; 2)
12 25 300
61
23
119
du (1;3; 2)
dx dy
dz
150
90
300

19.

7.6 ПОЛНОЕ ПРИРАЩЕНИЕ И ПОЛНЫЙ
ДИФФЕРЕНЦИАЛ
Применение дифференциала к приближённым вычислениям
Рассмотрим полное приращение функции z=f(х,у) :
1)
z f ( x x, y y ) f ( x, y )
2)
z z x ( x; y ) x z y ( x; y ) y x y
f ( x x, y y ) f ( x, y ) z x ( x; y ) x z y ( x; y ) y
Тогда
z ( x x, y y ) z ( x, y ) z x ( x; y ) x z y ( x; y ) y
Возьмём конкретную точку M 0 ( x0 ; y0 )
z ( x0 x, y0 y ) z ( x0 , y0 ) z x ( x0 ; y0 ) x z y ( x0 ; y0 ) y
Пример
Приближённо вычислить
1,07
4,94
Формула для приближённого
вычисления значения функции
z=f(х,у) в «неудобной» точке
M ( x0 x; y0 y )

20.

7.6 ПОЛНОЕ ПРИРАЩЕНИЕ И ПОЛНЫЙ
ДИФФЕРЕНЦИАЛ
Пример
Приближённо вычислить
1,07
4,94
.
z ( x0 x, y0 y ) z ( x0 , y0 ) z x ( x0 ; y0 ) x z y ( x0 ; y0 ) y
x 1,07 x0 1; x 0,07
z xy
z 1;5 15 1
y 4,94 y0 5; y 0,06
z x yx y 1
z x 1;5 5 14 5
z y x y ln x
z y 1;5 15 ln1 0
1,07
4,94
1 5 0,07 0 0,06 1 0,35 1,35

21.

ПРОДОЛЖЕНИЕ СЛЕДУЕТ...