Применение производной к исследованию и построению графиков функций

1. Применение производной к исследованию и построению графиков функций

2.

Одними из основных задач, возникающих при
исследовании функции, являются:
1) нахождение промежутков монотонности
функции
(промежутков
возрастания
и
убывания);
2) нахождение экстремумов функции (точки
минимума и максимума функции);
3) нахождение наибольшего и наименьшего
значений функции на промежутке.
Такой анализ легко сделать с помощью
производной.

3.

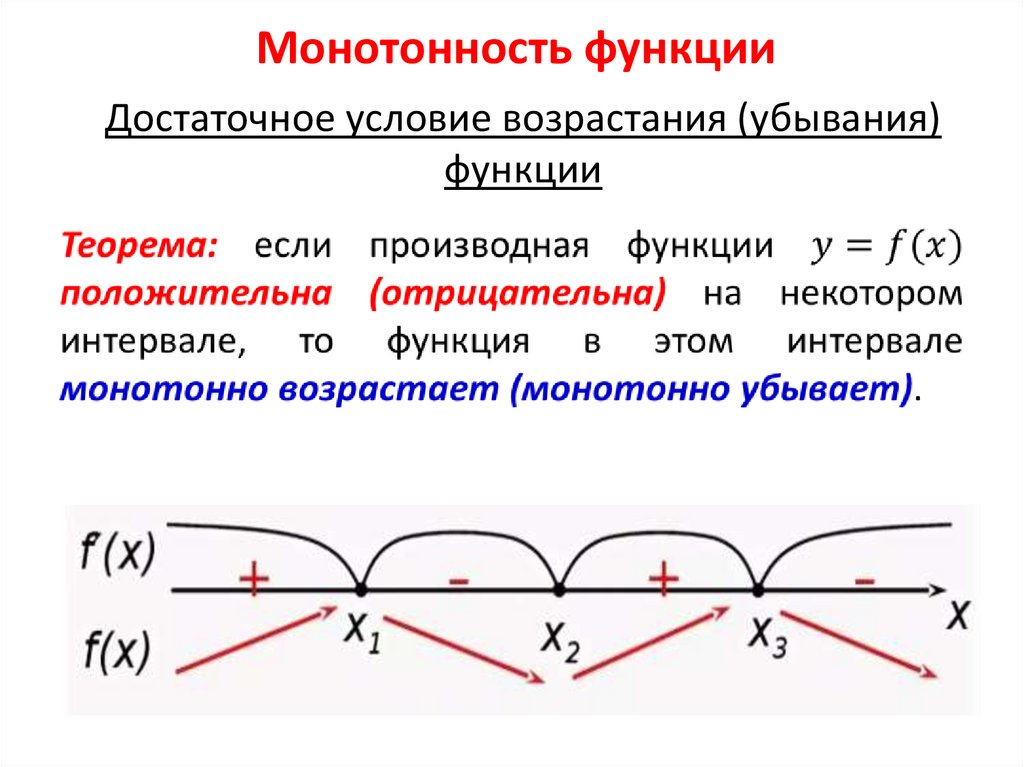
Монотонность функции
Достаточное условие возрастания (убывания)
функции

4.

Экстремумы функции
Определение: точки максимума и минимума
функции называются точками экстремума.

5.

Если производная меняет знак с + на –, то точка будет
являться точкой максимума, если с – на +, то точка
будет точкой минимума.

6.

Определение: точки в которых производная
функции
равна
нулю,
называются
стационарными точками функции, а точки в
которых производная не существует, критическими.

7.

8.

Правило нахождения интервалов
монотонности и экстремумов функции

9.

Пример №1. Найти промежутки монотонности
функции y=2x³-3x²-36x+5
1. Область определения: R. Функция непрерывна.
2. Вычисляем производную : y’=6x²-6x-36.
3. Находим критические точки: y’=0.
x²-x-6=0
Д=1-4*(-6)*1=1+24=25
4. Делим область определения на интервалы:
-
+
-2
+
3
5. Функция возрастает при xϵ(-∞;-2]υ[3;+∞),
убывает при xϵ[-2;3].
функция

10.

Пример №2. Найти промежутки монотонности
функции y=x³-3x²
1. Область определения: R. Функция непрерывна.
2. Вычисляем производную : y’=3x²-6x.
3. Находим критические точки: y’=0.
x²-2x=0
x(x-2)=0
x1=0 и x2=2
4. Делим область определения на интервалы:
+
0
2
5. Функция возрастает при xϵ(-∞;0]υ[2;+∞),
убывает при xϵ[0;2].
функция

11.

Пример №3. Найти экстремумы функции
y=-2x³-3x²+12x-4
1. Область определения: R. Функция непрерывна.
2. Вычисляем производную : y’=-6x²-6x+12.
3. Находим критические точки: y’=0.
-x²-x+2=0
Д=1-4*(-1)*2=1+8=9
x1=1; x2=-2
4. Делим область определения на интервалы:
+
-
-2
-
1
5. x=-2 – точка минимума. Найдём минимум функции
ymin=-24. x=1 – точка максимума. Найдём максимум
функции: ymax=3.

12.

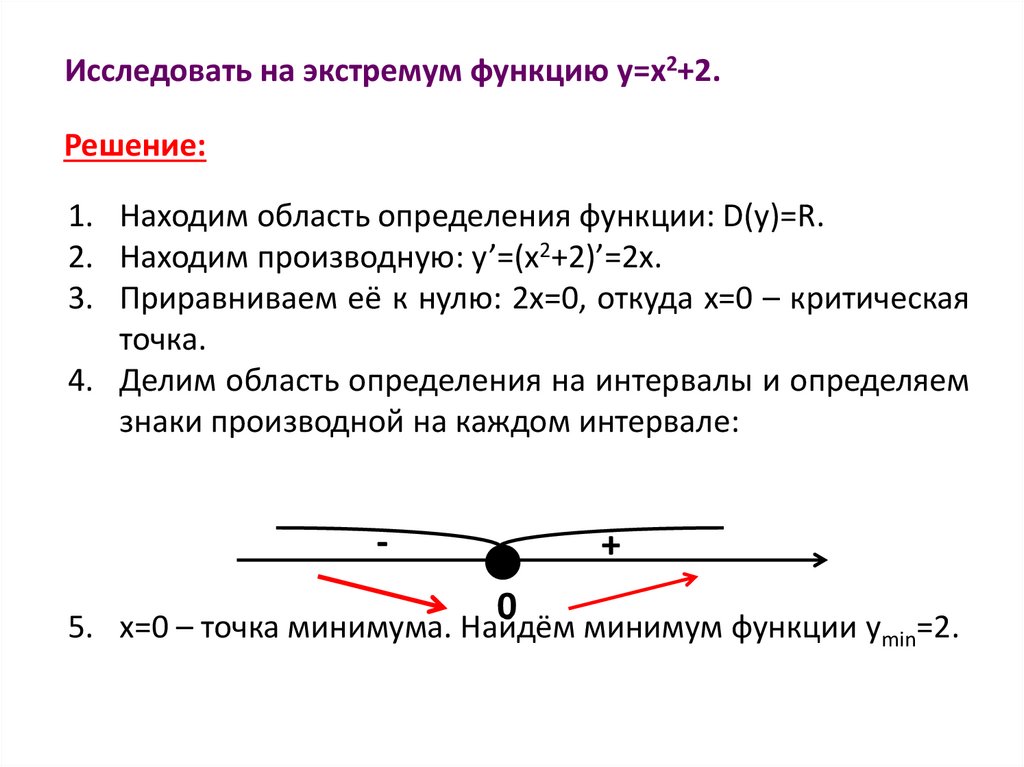
Исследовать на экстремум функцию y=x2+2.
Решение:
1. Находим область определения функции: D(y)=R.
2. Находим производную: y’=(x2+2)’=2x.
3. Приравниваем её к нулю: 2x=0, откуда x=0 – критическая
точка.
4. Делим область определения на интервалы и определяем
знаки производной на каждом интервале:
-
+
0
5. x=0 – точка минимума. Найдём минимум функции ymin=2.

13.

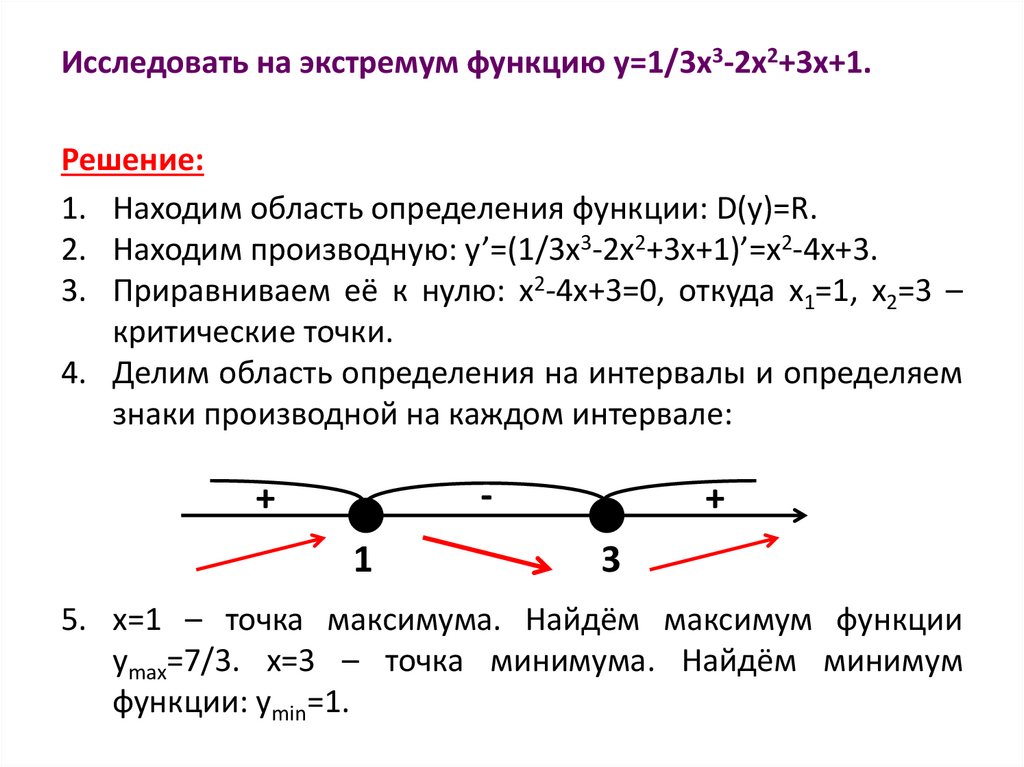
Исследовать на экстремум функцию y=1/3x3-2x2+3x+1.
Решение:
1. Находим область определения функции: D(y)=R.
2. Находим производную: y’=(1/3x3-2x2+3x+1)’=x2-4x+3.
3. Приравниваем её к нулю: x2-4x+3=0, откуда x1=1, x2=3 –
критические точки.
4. Делим область определения на интервалы и определяем
знаки производной на каждом интервале:
-
+
1
+
3
5. x=1 – точка максимума. Найдём максимум функции
ymax=7/3. x=3 – точка минимума. Найдём минимум
функции: ymin=1.

14.

Исследовать на экстремум функцию y=x3+3x2+9x-6.
Решение:
1. Находим область определения функции: D(y)=R.
2. Находим производную: y’=(x3+3x2+9x-6)’=3x2+6x+9.
3. Приравниваем её к нулю: 3x2+6x+9=0, откуда D<0. То есть
критических точек не существует.
4. Однако, функция возрастает на всей D(y), так как
y’=3x2+6x+9 >0:

15.

Исследовать на экстремум функцию y=x2-x-6.
Решение:
1. Находим область определения функции: D(y)=R.
2. Находим производную: y’=(x2-x-6)’=2x-1.
3. Приравниваем её к нулю: 2x-1=0, откуда x=1/2 –
критическая точка.
4. Делим область определения на интервалы и определяем
знаки производной на каждом интервале:
-
+
1/2
5. x=1/2 – точка минимума. Найдём минимум функции:
ymin=-6,25.

16.

17. Спасибо за внимание !!!