Дискретная случайная величина. Закон распределения

1.

Задание: Прочитать. Конспект
(кадры 1,2,3,4). Знать, по каким
формулам вычисляется
математическое ожидание,
дисперсия, среднее квадратическое
отклонение.

2.

Дискретная
•случайная величина.
Закон распределения.
Тема:

3.

Случайной величиной называется величина, которая в результате опыта
может принять то или иное значение, неизвестно заранее, какое именно.
Дискретной (прерывной) случайной величиной называется
случайная величина, принимающая отдельные друг от друга
значения, которые можно перенумеровать.
Непрерывной случайной величиной называется случайная величина,
возможные значения которой непрерывно заполняют какой-то промежуток.
Законом распределения случайной величины называется
всякое
соотношение,
устанавливающее
связь
между
возможными
значениями
случайной
величины
и
соответствующими им вероятностями. Закон распределения
может иметь разные формы.
Рядом распределения дискретной случайной величины Х называется
таблица, где перечислены возможные (различные) значения этой случайной
величины х1, х2, ..., хn с соответствующими им вероятностями р1, р2, ..., рn.

4.

X
…
P
…
X – случайная величина,
,…,
- перечень всех возможных значений случайной величины X,
,…,
- соответствующие им вероятности.
Такую таблицу называют
законом распределения дискретной
случайной величины.

5.

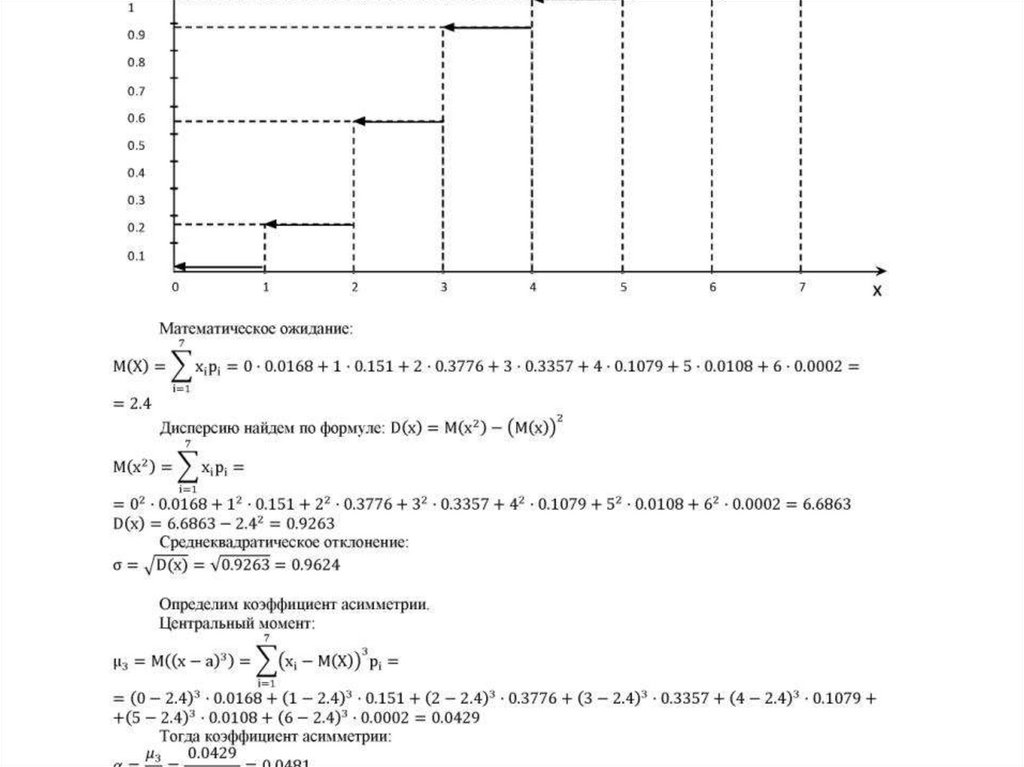
Характеристики закона распределения
Математическим ожиданием называется
средняя величина возможных значений случайных
величин, взвешенных по их вероятности.
Выражается формулой:
M (X) =
+
…+
Дисперсией (рассеянием) дискретной случайной
величины называется математическое ожидание квадрата отклонения
случайных величин от математического ожидания:
D[Х]=M[X-M(X)]2 = M(X2) -[M(X)]2
D[Х]= M(X2) -[M(X)]2
Среднее квадратическое отклонение
вычисляется по формуле:
σ =