Кинематика точки. Лекция №2.1

1.

Лекция № 2.1
Учебная дисциплина: Теоретическая механика
Раздел: Кинематика
Тема:
Кинематика точки.
Учебные вопросы:
1.
Основные понятия кинематики.
2.
Способы задания движения точки.
3.
Частные случаи движения точки.

2.

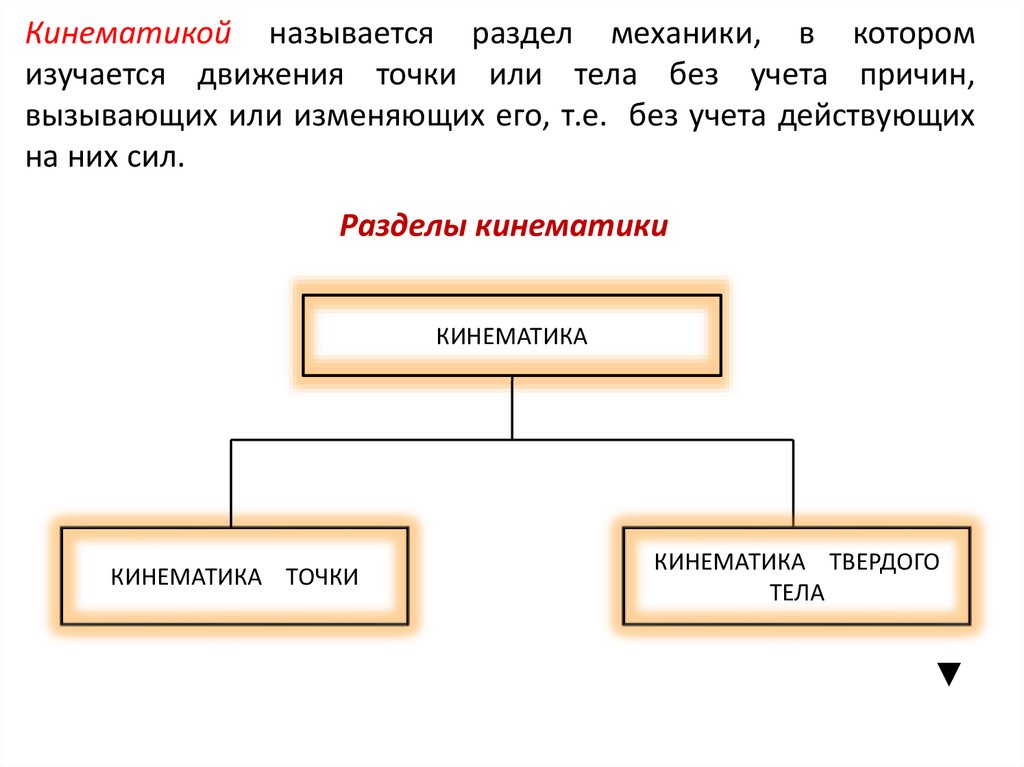
Кинематикой называется раздел механики, в котором
изучается движения точки или тела без учета причин,
вызывающих или изменяющих его, т.е. без учета действующих
на них сил.
Разделы кинематики
КИНЕМАТИКА
КИНЕМАТИКА ТОЧКИ
КИНЕМАТИКА ТВЕРДОГО
ТЕЛА
▼

3.

Основные задачи кинематики точки
описание способов задания движения точки;
определение кинематических характеристик движения точки
(скорости, ускорения).
Скорость точки – это величина, которая характеризует как быстро и в каком
направлении меняется положение точки в пространстве.
Ускорение точки – это мера движения, которая характеризует как быстро и в
каком направлении меняется скорость точки в пространстве.
Для решения задач кинематики необходимо, чтобы изучаемое движение было
каким-либо образом задано (описано).
Задать движение или закон движения тела (точки) относительно какойнибудь системы отсчета − значит задать условия, позволяющие определить
положение этого тела относительно данной системы отсчета в любой
момент времени.

4.

СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИ ТОЧКИ
1. Векторный способ задания движения
2. Координатный способ задания движения
3. Естественный способ задания движения

5.

Векторный способ задания движения точки состоит в том, что
задается закон изменения радиус−вектора движущейся точки
М как функции времени:
М
z
О
y
x
Это равенство называется векторным уравнением движения
точки или законом движения точки в векторной форме.

6.

Определение скорости точки
Пусть
– радиус−вектор, определяющий положение точки
М в момент времени t;
М
z
М1
О
y
x
– радиус−вектор, определяющий положение
точки М в момент времени
t1 = t + Δt
▼

7.

Тогда
где
М
z
М1
О
y
x
▼

8.

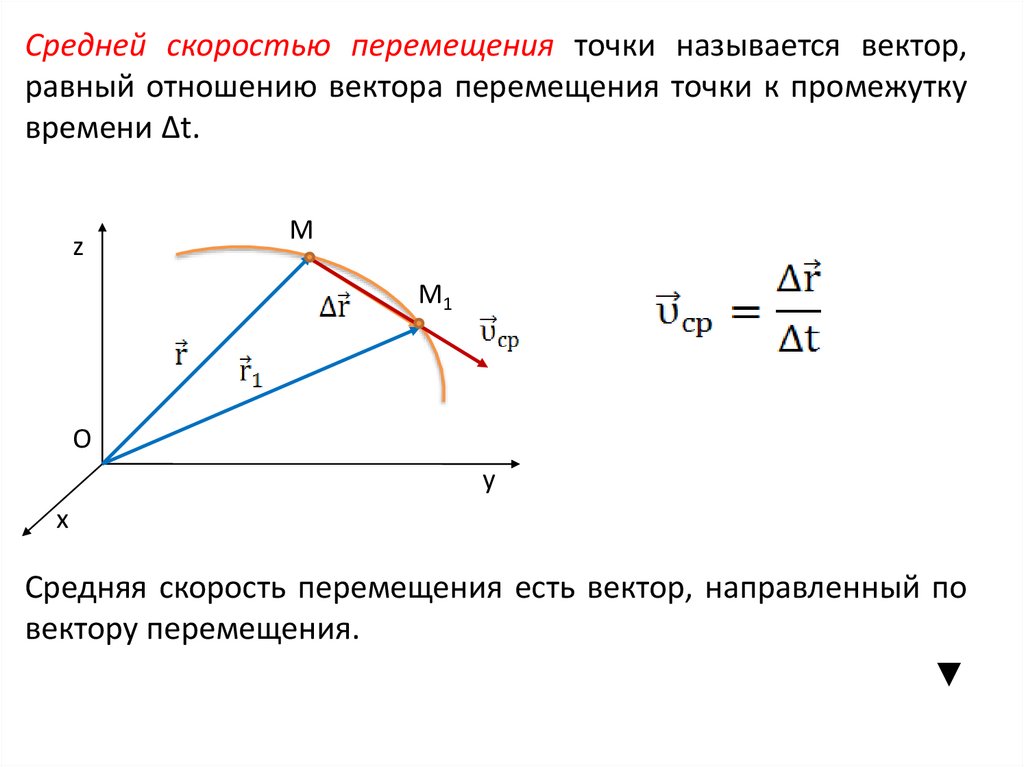
Средней скоростью перемещения точки называется вектор,
равный отношению вектора перемещения точки к промежутку
времени Δt.
z
М
М1
О
y
x
Средняя скорость перемещения есть вектор, направленный по
вектору перемещения.
▼

9.

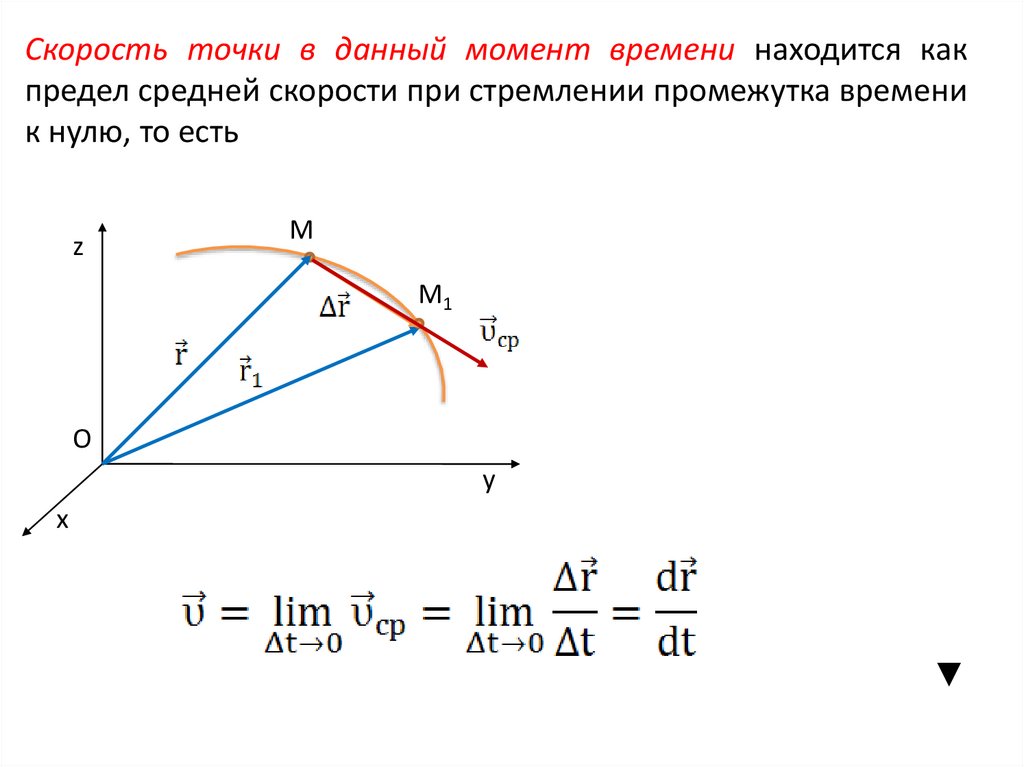
Скорость точки в данный момент времени находится как
предел средней скорости при стремлении промежутка времени
к нулю, то есть
z
М
М1
О
y
x
▼

10.

Следовательно,
Скорость точки в данный момент времени равна векторной
производной от радиуса−вектора точки по времени.
z
М
М1
О
y
x
Вектор скорости направлен по касательной к траектории точки
в сторону движения.
▼

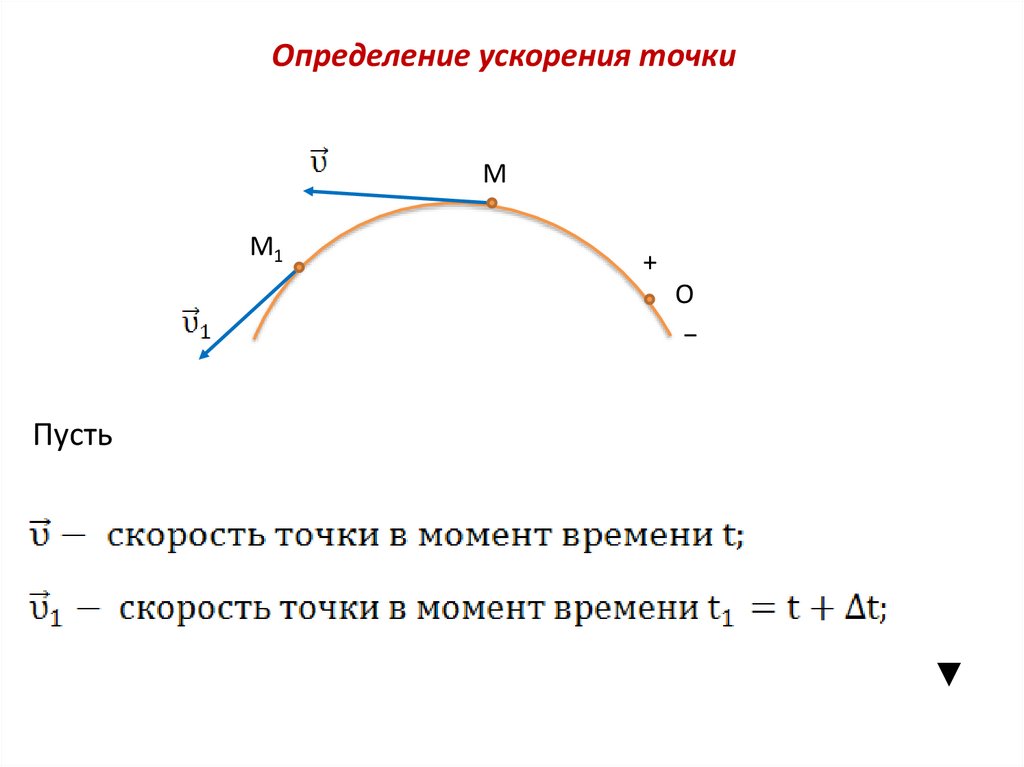
11.

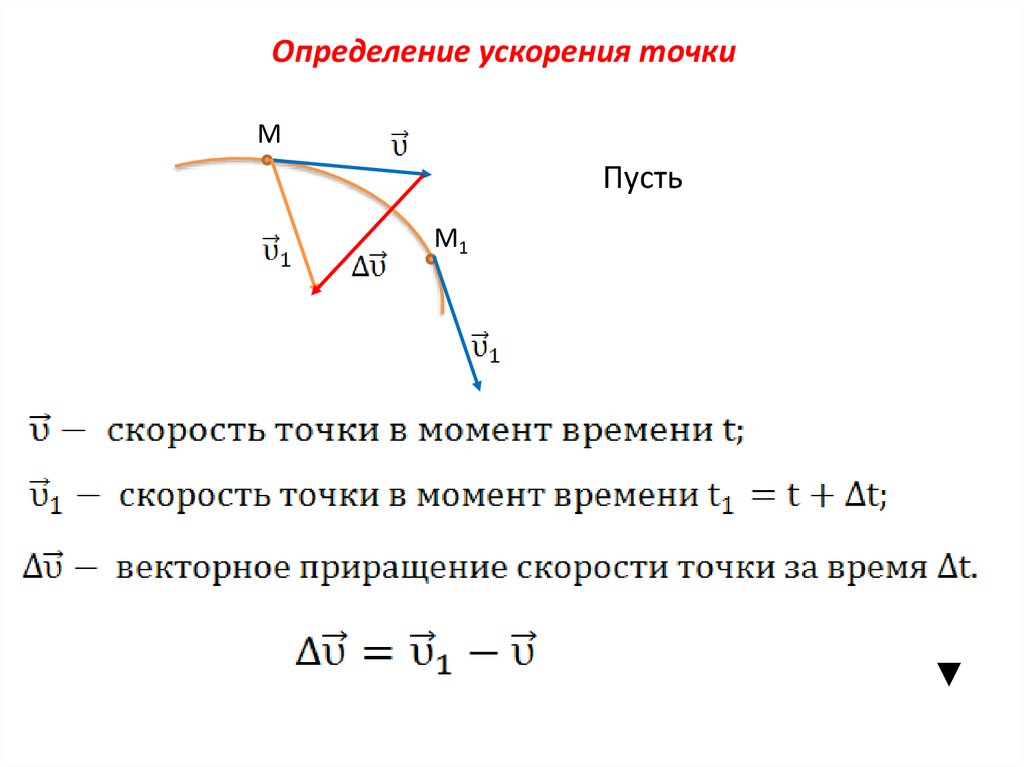
Определение ускорения точки
М
Пусть
М1
▼

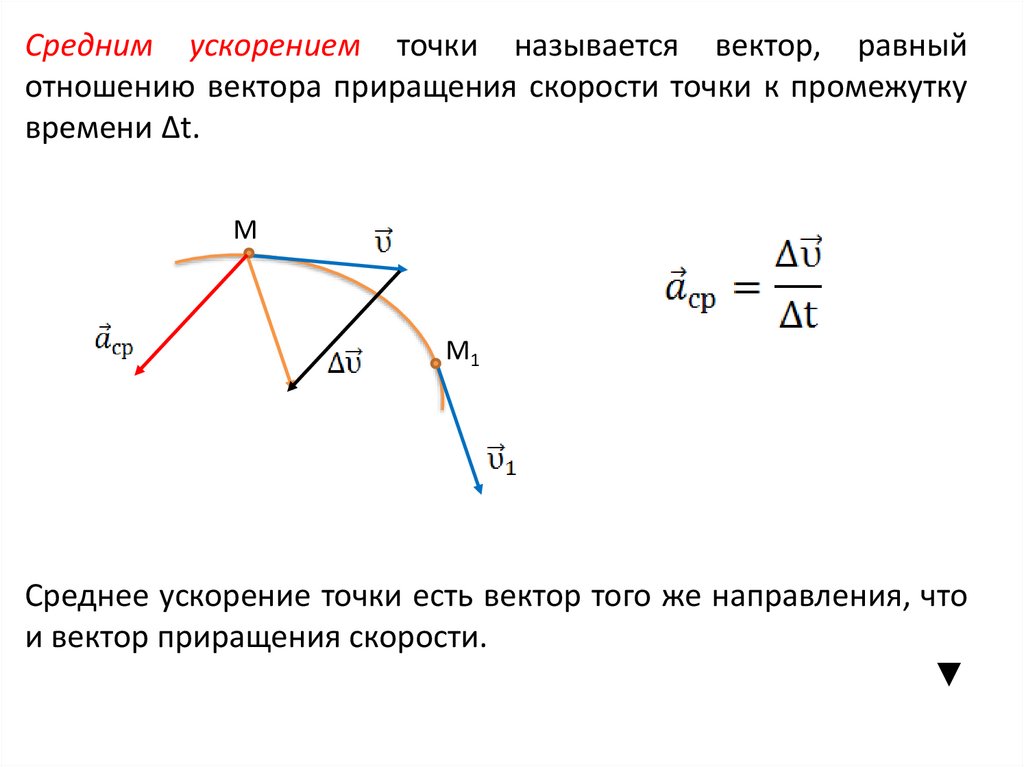
12.

Средним ускорением точки называется вектор, равный
отношению вектора приращения скорости точки к промежутку
времени Δt.
М
М1
Среднее ускорение точки есть вектор того же направления, что
и вектор приращения скорости.
▼

13.

Ускорением в данный момент времени называется
предельное значение среднего ускорения при стремлении
промежутка времени к нулю, то есть
М
М1
▼

14.

Таким образом:
Ускорение точки есть вектор, равный первой производной
вектора скорости по времени или второй производной от
радиуса−вектора точки по времени.
Вектор ускорения
траектории.
направлен
в
сторону
вогнутости
▼

15.

Координатный способ задания движения точки состоит в том,
что в некоторой системе отсчета Оxyz задаются координаты
движущейся точки М как функции времени:
z
x = x(t)
М
y = y(t)
z(t)
x(t)
x
О
z = z(t)
y(t)
y
▼

16.

Эти уравнения, заданием которых полностью определяется
движение точки, называются уравнениями движения точки в
координатной форме.
Уравнения являются параметрическими, в которых роль
параметра играет время t.
По ним легко определить уравнение траектории точки в
декартовых координатах.
Чтобы записать уравнение траектории в явном форме, надо
исключить из них время.
▼

17.

Как известно из математики, радиус−вектор выражается
формулой:
(1)
где
x (t), y (t), z (t) − проекции радиус−вектора на
декартовой системы координат;
оси
Формула (1) выражает связь между координатным и
векторным способами задания движения.
▼

18.

Определение скорости точки
По определению
Так как
Следовательно,
▼

19.

Продифференцировав выражение, получаем:
С другой стороны
Следовательно,
Проекции скорости точки на оси неподвижных декартовых
координат равны первым производным от соответствующих
координат точки по времени.
▼

20.

Определение ускорения точки
Из определения ускорения:
Так как
Следовательно,
▼

21.

Продифференцировав выражение, получаем:
С другой стороны
Следовательно,
Проекции ускорения точки на оси неподвижных декартовых
координат
равны
вторым
производным
от
соответствующих координат точки по времени.
▼

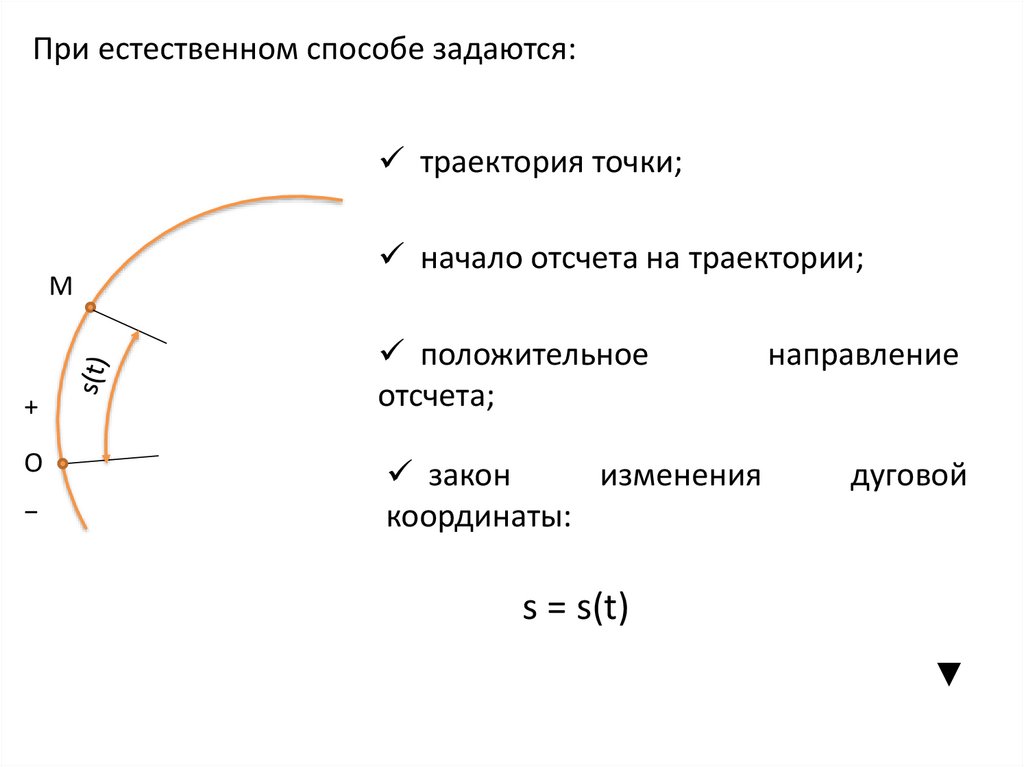
22.

При естественном способе задаются:
траектория точки;
М
+
О
−
начало отсчета на траектории;
положительное
отсчета;
закон
изменения
координаты:
направление
дуговой
s = s(t)
▼

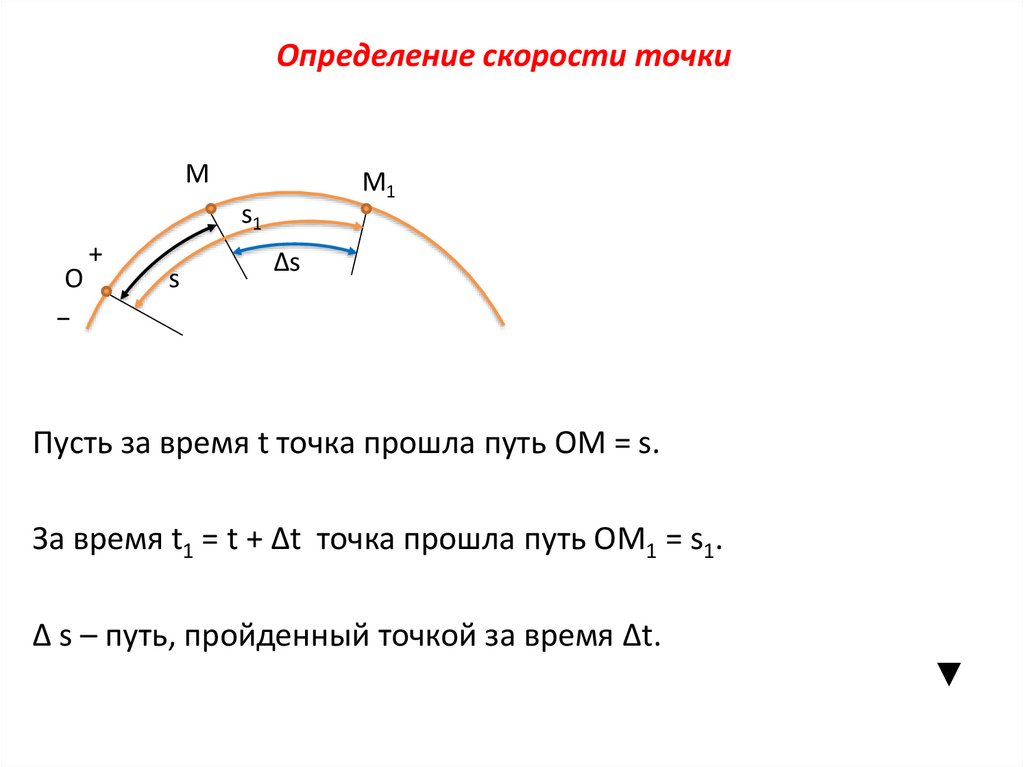
23.

Определение скорости точки
М
М1
s1
О
−
+
s
Δs
Пусть за время t точка прошла путь ОМ = s.
За время t1 = t + Δt точка прошла путь ОМ1 = s1.
Δ s – путь, пройденный точкой за время Δt.
▼

24.

Отношение пройденного пути Δs к промежутку времени Δt
называется средней скоростью точки за время Δt.
Скорость точки в данный момент времени находится как
предел средней скорости при стремлении промежутка времени
к нулю, то есть
▼

25.

Следовательно,
Алгебраическое значение скорости в данный момент времени
равно производной от дуговой координаты по времени.
М
Вектор скорости направлен по касательной к траектории точки
в сторону движения.
▼

26.

Определение ускорения точки
М
М1
+
О
−
Пусть
▼

27.

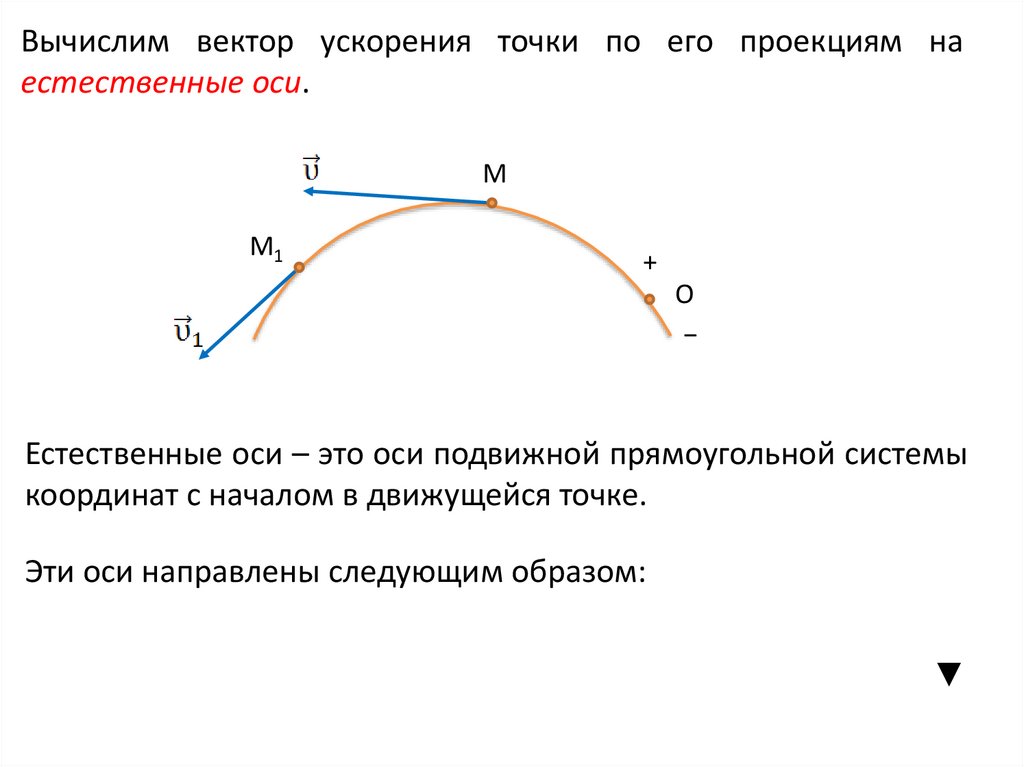
Вычислим вектор ускорения точки по его проекциям на
естественные оси.
М
М1
+
О
−
Естественные оси – это оси подвижной прямоугольной системы
координат с началом в движущейся точке.
Эти оси направлены следующим образом:
▼

28.

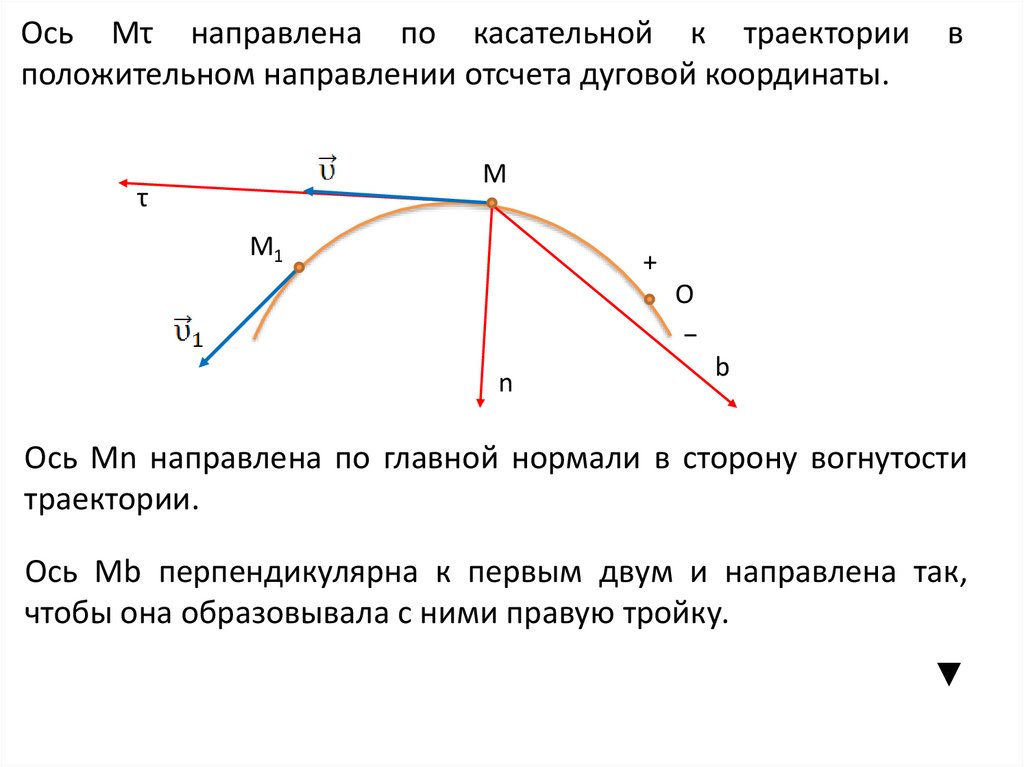
Ось Мτ направлена по касательной к траектории
положительном направлении отсчета дуговой координаты.
в
М
τ
М1
+
О
−
n
b
Ось Мn направлена по главной нормали в сторону вогнутости
траектории.
Ось Мb перпендикулярна к первым двум и направлена так,
чтобы она образовывала с ними правую тройку.
▼

29.

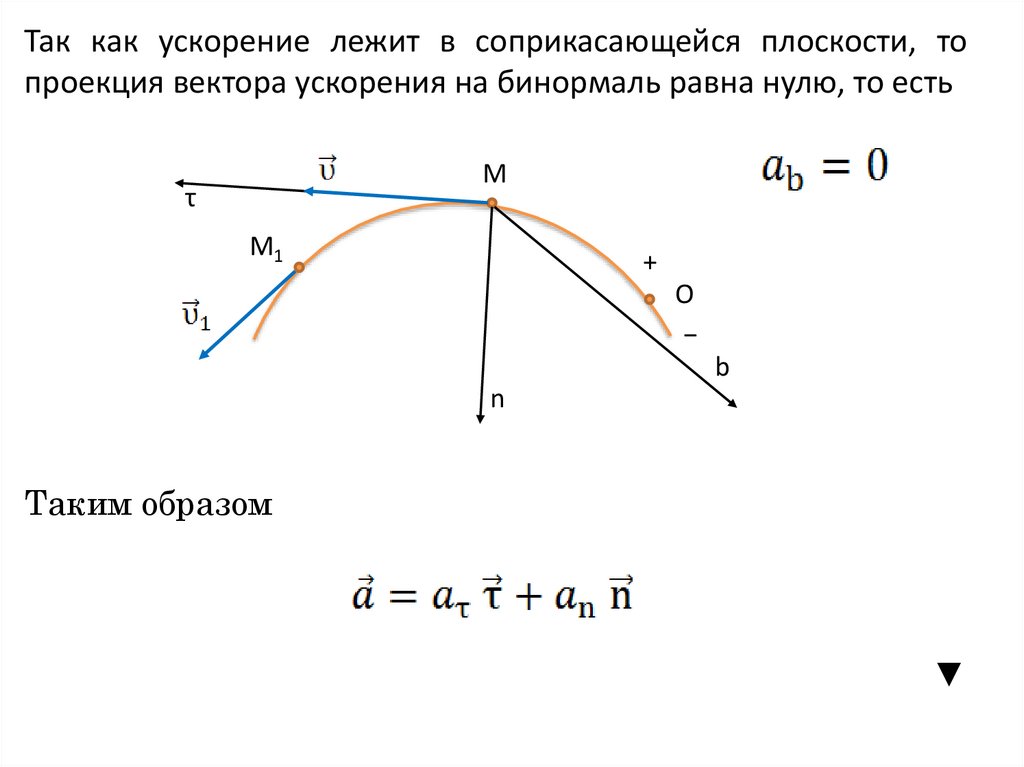
Так как ускорение лежит в соприкасающейся плоскости, то
проекция вектора ускорения на бинормаль равна нулю, то есть
М
τ
М1
+
О
−
b
n
Таким образом
▼

30.

где
τ
М
+
О
−
b
n
Проекция ускорения точки на касательную равна
первой производной от численной величины скорости
или второй производной от дуговой координаты по
времени.
Эта составляющая характеризует изменение скорости
по модулю.
▼

31.

τ
М
+
О
−
b
n
Проекция ускорения на главную нормаль равна
квадрату скорости, деленному на радиус кривизны
траектории в данной точке кривой.
Эта составляющая характеризует изменение скорости
по направлению.
▼

32.

Вектор
ускорения
точки
изображается
диагональю
параллелограмма, построенного на касательной и нормальной
составляющих.
τ
М
+
О
−
b
n
Так как эти составляющие взаимно перпендикулярны, то по
модулю
▼

33.

Равномерное движение точки
Движение точки называется равномерным, если модуль ее
скорости не изменяется во время движения, то есть
Уравнение равномерного движения точки имеет вид:
▼

34.

Равнопеременное движение точки
Равнопеременным движением точки называется такое
движение, при котором касательное ускорение является
величиной постоянной, то есть
Уравнение равнопеременного движения точки имеет вид:
▼

35.

Если
то равнопеременное
равноускоренным.
движение
называется
то равнопеременное
равнозамедленным.
движение
называется
▼

36.

Если движение равномерное, то
Следовательно,
Если движение прямолинейное, то
Следовательно,
▼

37.

1. Движение равномерное и прямолинейное.
Следовательно,
М
▼

38.

2. Движение переменное и прямолинейное.
Следовательно,
М
Приведен случай замедленного движения.
▼

39.

3. Движение равномерное и криволинейное.
Следовательно,
М
▼

40.

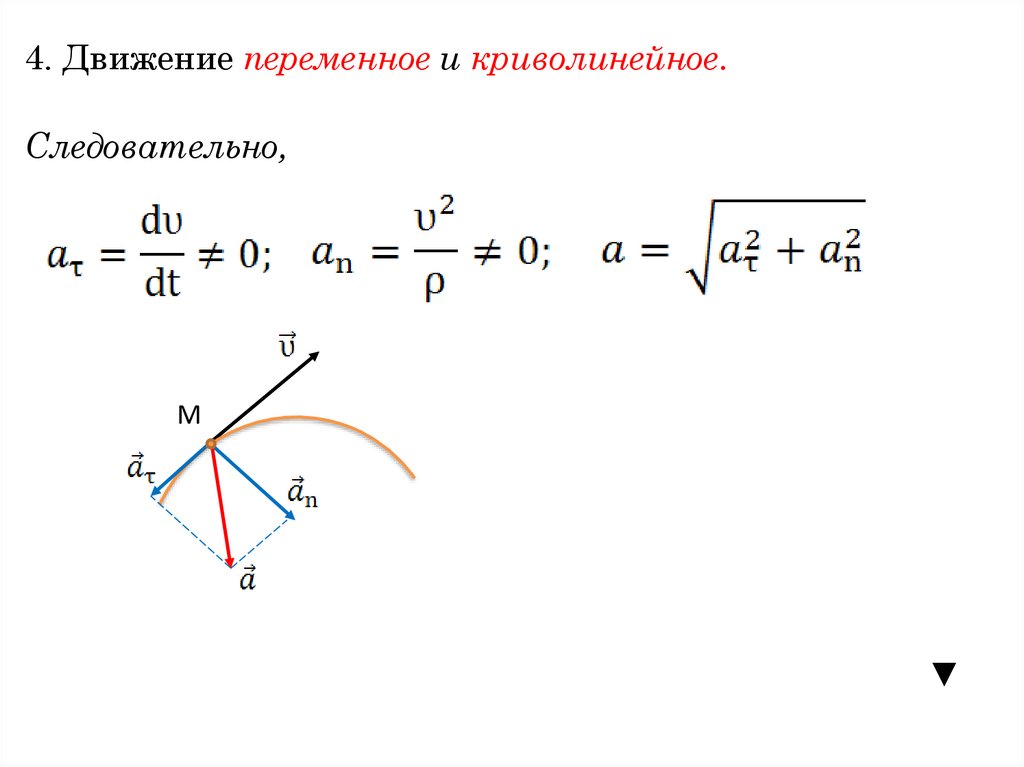
4. Движение переменное и криволинейное.
Следовательно,
М
▼

41.

Пример
По заданному уравнению движения точки М установить вид ее
траектории и для момента времени t = t1 найти положение
точки на траектории, ее скорость, полное, касательное и
нормальное ускорение, а также радиус кривизны.
(1)
при
▼

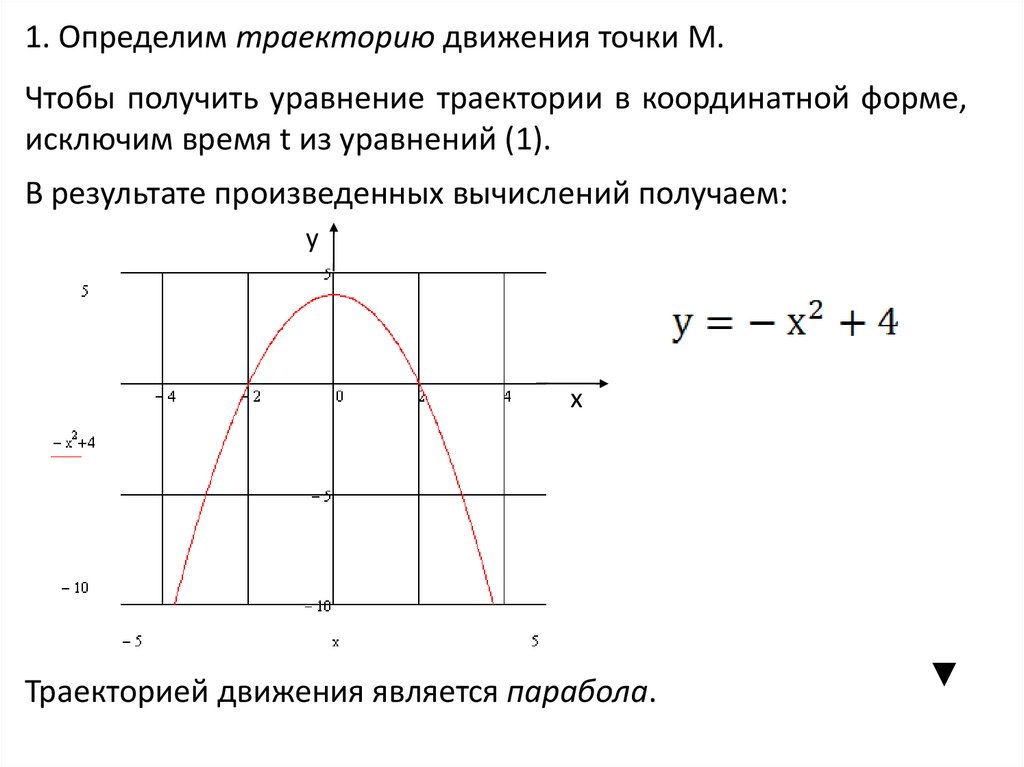
42.

1. Определим траекторию движения точки М.
Чтобы получить уравнение траектории в координатной форме,
исключим время t из уравнений (1).
В результате произведенных вычислений получаем:
y
x
Траекторией движения является парабола.
▼

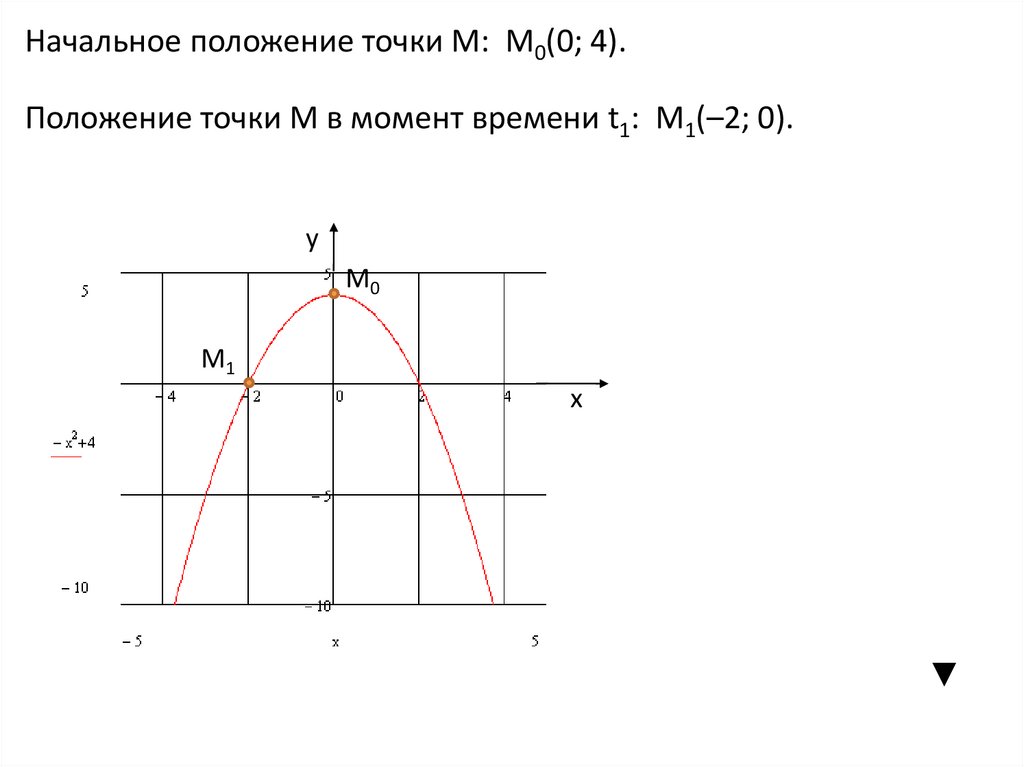
43.

Начальное положение точки М: М0(0; 4).
Положение точки М в момент времени t1: М1(–2; 0).
y
М0
М1
x
▼

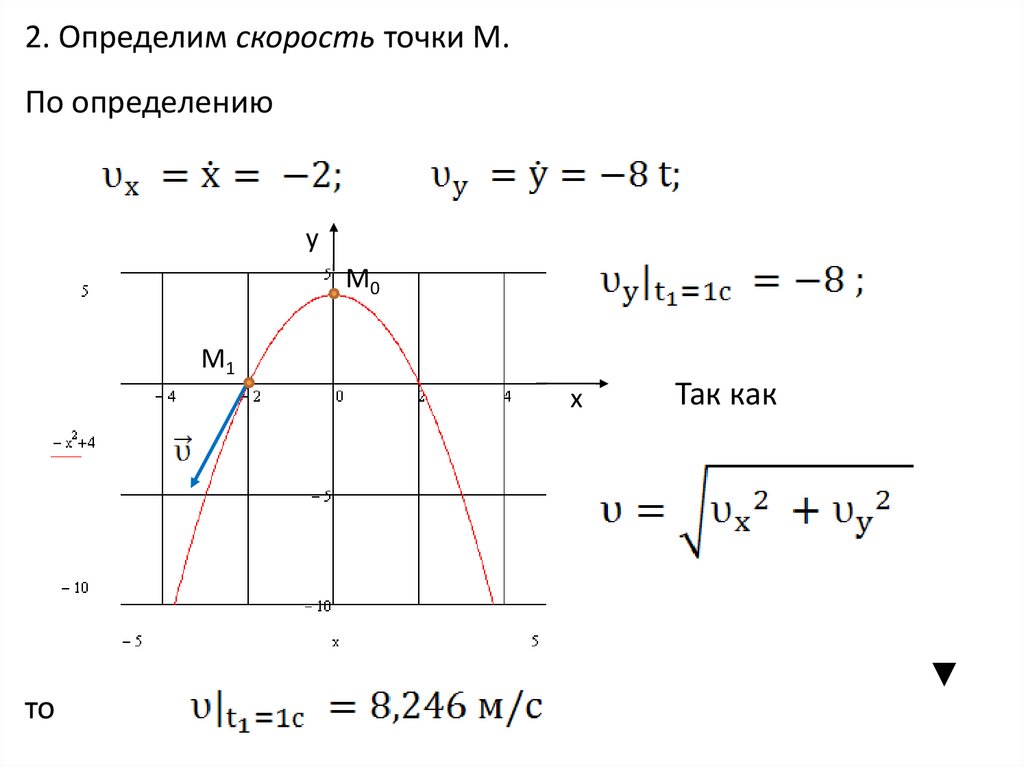
44.

2. Определим скорость точки М.
По определению
y
М0
М1
x
то
Так как
▼

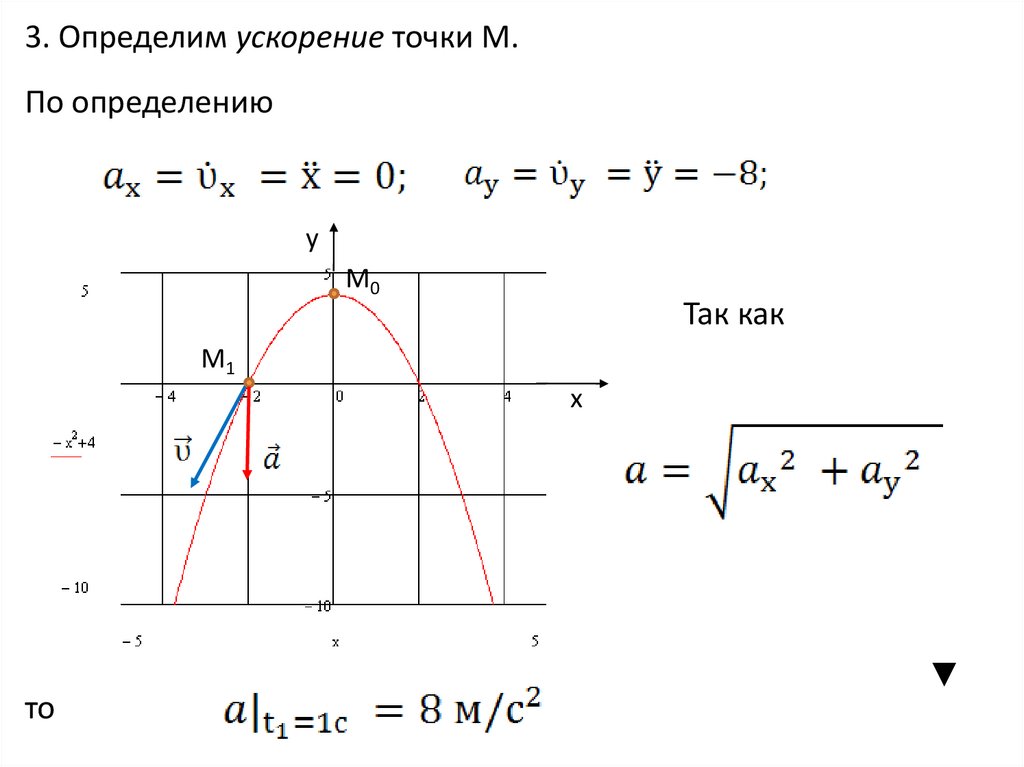
45.

3. Определим ускорение точки М.
По определению
y
М0
Так как
М1
x
то
▼

46.

4. Определим радиус кривизны траектории в точке М.
По определению
Так как
где
или
Окончательно получаем:
▼