Похожие презентации:
Кинематика точки
1. Кинематика точки
2.
Предмет кинематики
Способы задания движения точки
Скорость точки
Ускорение точки
Равномерное и равнопеременное
движение точки
3. Предмет кинематики
• Кинематика – раздел теоретической механики, вкотором описываются способы задания движения
объекта, определяются кинематические
характеристики движения объекта (линейной или
угловой скорости, ускорения)
• Задать движение – описать способ, с помощью
которого можно определить положение объекта
(точек объекта) в любой момент времени по
отношению к выбранной системе отсчета
• В качестве объекта в кинематике точки
рассматривается геометрическая точка
4. Способы задания движения точки
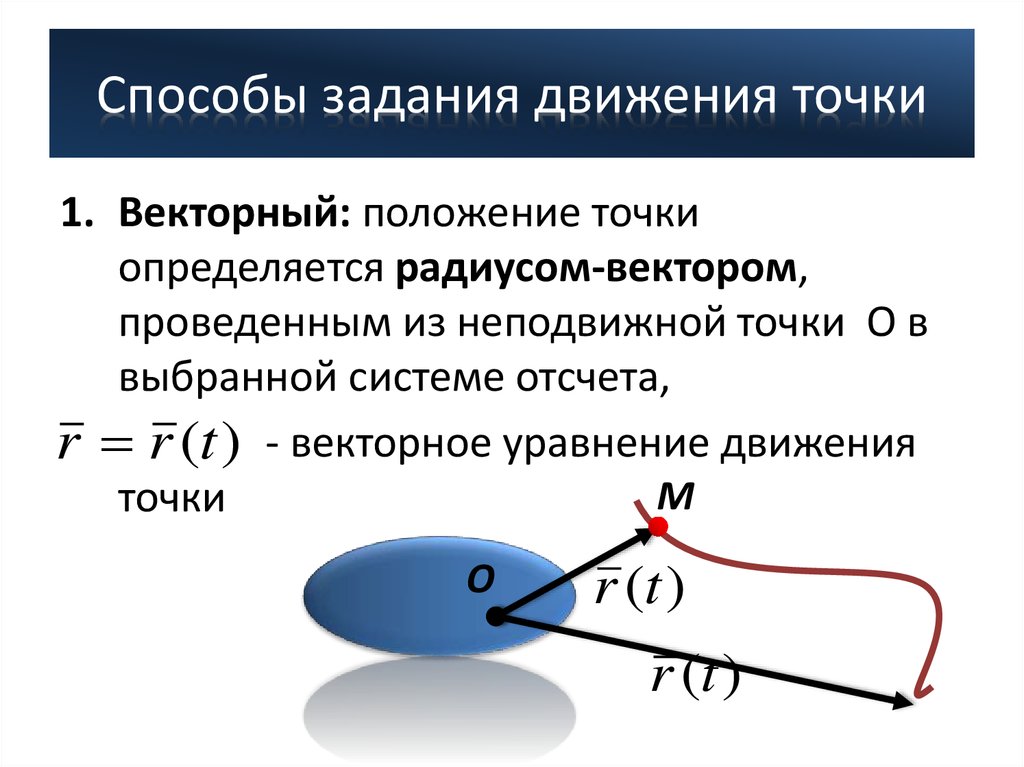
1. Векторный: положение точкиопределяется радиусом-вектором,
проведенным из неподвижной точки O в
выбранной системе отсчета,
r r (t ) - векторное уравнение движения
M
точки
O
r (t )
r (t )
5.
2. Координатный : положение точкиопределяется координатами точки,
являющимися функциями времени
x x(t ),
y y (t ),
z z (t )
- уравнения движения точки в координатной
форме
M
z
O
x(t)
x
r (t )
y(t)
z(t)
y
6.
2. Естественный: положение точкиопределяется траекторией движения,
началом отсчета О на траектории с
указанием положительного направления
(+) движения, законом изменения дуговой
координаты s s (t )
-
+
O
s (t ) M
7.
• Траектория точки – геометрическое местоположений движущейся точки в
рассматриваемой системе отсчета
• Задание 1. Точка М совершает движение из
начала отсчета О в отрицательном
направлении: прошла путь 17 метров и
вернулась в точку O. Определить конечное
значение дуговой координаты.
8. Скорость точки
Вектор скорости – вектор, равныйdr
dt
r r (t ) - радиус-вектор точки М
Скорость – кинематическая мера движения
точки, проекция вектора скорости на
положительное направление
касательной к траектории
ds
dt
Касательная к
траектории
s-закон изменения дуговой координаты
M
9.
Для координат (проекций) вектора скорости( x ; y ; z )
на оси системы координат Oxyz имеем
x x' ; y y ' ; z z ' ;
M
z
r (t )
O
k
x(t) i j
x
z(t)
y
y(t)
10. Ускорение точки
Вектор ускорения – вектор, равныйd
d r
a
2
dt
dt
r r (t ) - радиус-вектор точки М
2
Ускорение – мера изменения скорости точки.
Модуль вектора ускорения
d 2s
a ' 2 ,
dt
2
an
Касательная к
траектории
s-закон изменения дуговой координаты
a
M
a
an
11.
• Радиус кривизны траектории – радиусокружности, которая описывает поведение
траектории в окрестности данной точки
a n - нормальное ускорение точки
a - тангенциальное ускорение точки
! Если движение точки прямолинейное
(траектория движения - прямая), то
an 0,
12.
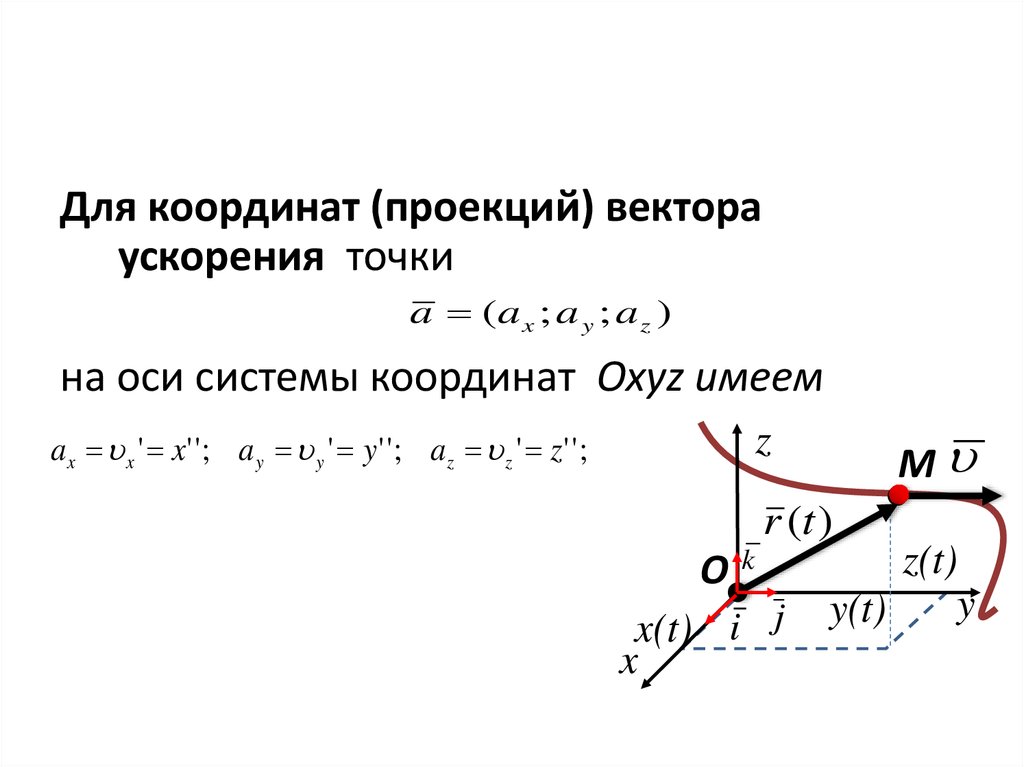
Для координат (проекций) вектораускорения точки
a (a x ; a y ; a z )
на оси системы координат Oxyz имеем
M
z
a x x ' x' ' ; a y y ' y ' ' ; a z z ' z ' ' ;
r (t )
O
k
x(t) i j
x
z(t)
y
y(t)
13. Равномерное и равнопеременное движение точки
• Движение• Движение
называется
называется
равнопеременным,
равномерным, если
если a const
const
и следовательно
aM , 0,
s s0 M , 0t
M M ,0 aM , t ,
s s0 M , 0t
aM , t 2
2











 Физика
Физика








