Похожие презентации:
Кинематика. Кинематика точки
1. 1. КИНЕМАТИКА. Кинематика точки.
• Кинематика точки• Кинематика – раздел механики, в котором изучаются
геометрические свойства движения тел. При этом не
учитываются масса тел и силы, которые действуют на них.
• Все величины в кинематике рассматриваются как изменяющиеся
с течением времени, т.е. как функции времени.
2. 2. Кинематика.
• Векторный способ задания движения точки.• Положение точки М задается ее радиусом-вектором
,
проведенным из начала координат О в точку М (рис.37).
r
Рис.37.
• При движении точки М вектор r рассматривается как переменный
вектор (вектор-функция), зависящий от аргумента t:
- уравнение движения или закон движения точки
r r t
в векторной форме.
• В прямоугольных декартовых координатах проекции вектора r на
оси x, y, z (рис.37): r x,..r y,..r z .
x
y
z
3. 3. Кинематика.
• Координатный способ задания движения точки.• Положение точки можно задать ее координатами x, y, z,
изменяющимися с течением времени.
x f t ; y f 2 t ; z f 3 t
1
• - уравнения движения точки или закон движения точки.
Из этих уравнений, исключая время t, можно найти уравнения
траектории движения точки.
4. 4. Кинематика.
• Естественный способ задания движения.• Траектория точки М – кривая АВ – известна (рис.38). Точку
O примем за
начало отсчета. Определим положительное и отрицательное направление отсчета движения точки на кривой.
• s – криволинейная координата, равная расстоянию от точки O
до точки М ( M1 , M 2 ,…).
Рис. 38.
s=f(t) - закон движения точки М вдоль траектории.
5. 5. Кинематика.
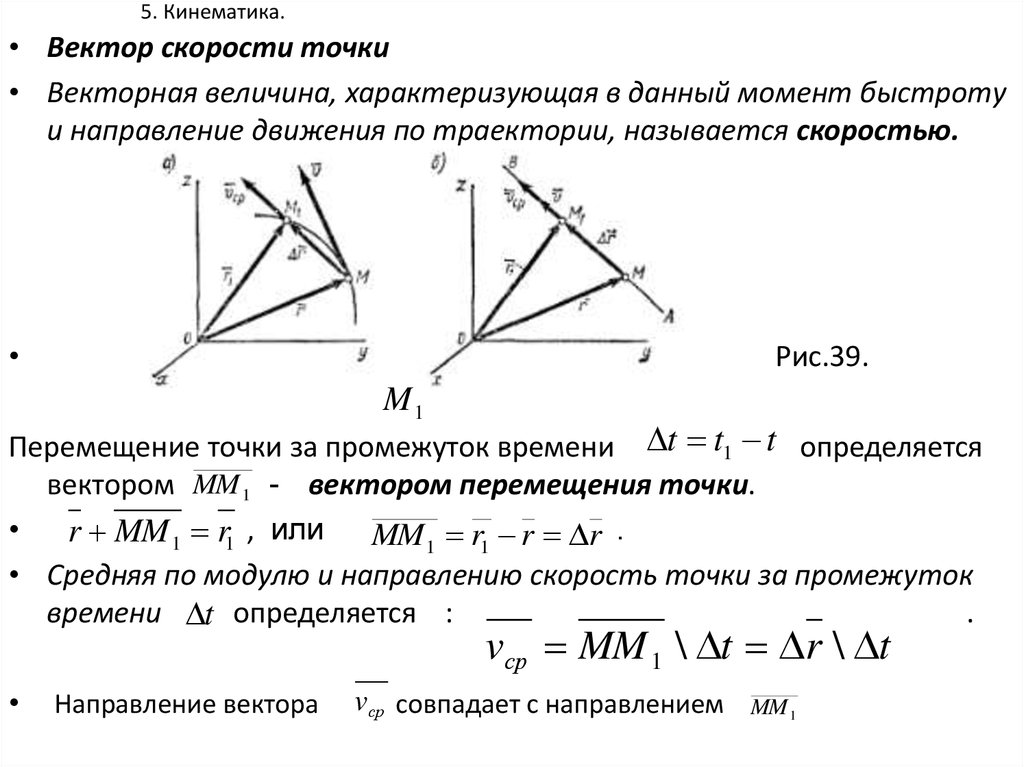
• Вектор скорости точки• Векторная величина, характеризующая в данный момент быстроту
и направление движения по траектории, называется скоростью.
Рис.39.
M1
Перемещение точки за промежуток времени t t1 t определяется
вектором MM 1 - вектором перемещения точки.
r MM 1 r1 , или MM 1 r1 r r .
• Средняя по модулю и направлению скорость точки за промежуток
времени t определяется :
.
vср MM 1 \ t r \ t
Направление вектора
vср совпадает с направлением
MM 1
6. 6. Кинематика. Вектор скорости точки.
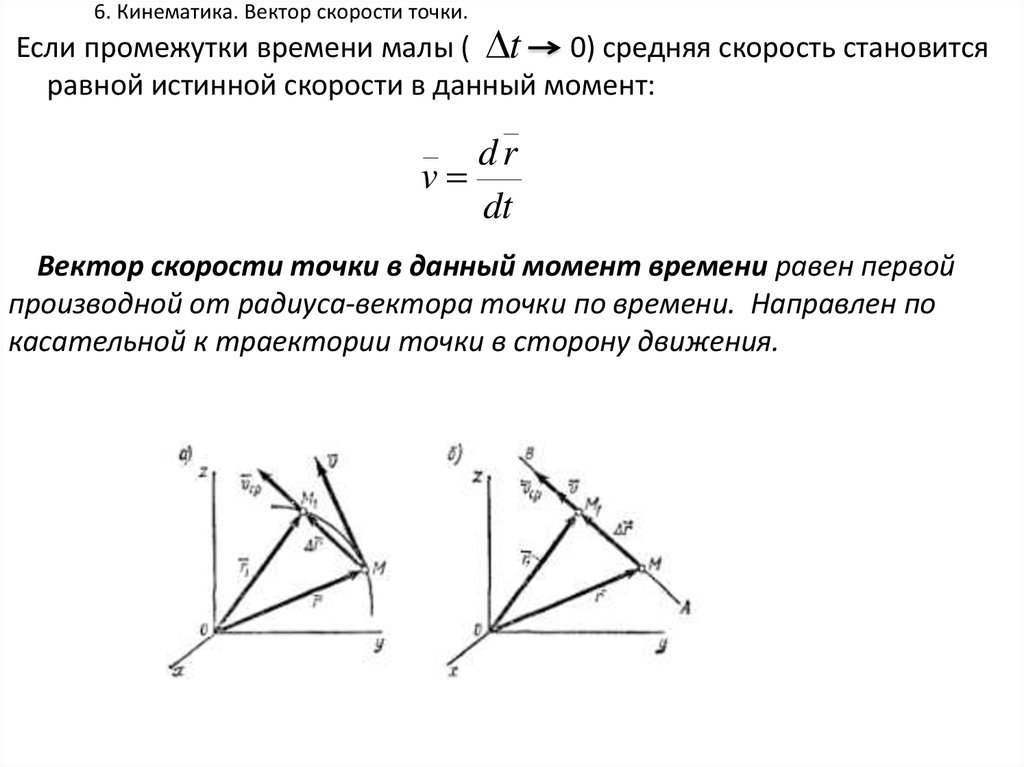
Если промежутки времени малы ( t0) средняя скорость становится
равной истинной скорости в данный момент:
dr
v
dt
Вектор скорости точки в данный момент времени равен первой
производной от радиуса-вектора точки по времени. Направлен по
касательной к траектории точки в сторону движения.
7. 7. Кинематика.
• Вектор ускорения точки• Ускорением точки называется векторная величина,
характеризующая изменение с течением времени модуля и
направления скорости точки.
dv d 2 r
a
2.
dt
dt
Вектор направлен в сторону вогнутости траектории.
• Вектор ускорения a лежит в соприкасающейся плоскости и направлен в
сторону вогнутости кривой.
Плоскость, в которой происходит бесконечно малый поворот касательной к траектории при
элементарном перемещении движущейся точки. Для плоской кривой соприкасающаяся плоскость
совпадает с плоскостью этой кривой и является общей для всех точек.
8. 8. Кинематика.
• Скорость и ускорение точки при координатном способе,
задания движения
Воспользуемся теоремой: проекция производной от вектора на ось, неподвижную в данной
системе отсчета, равна производной от проекций дифференцируемого вектора на ту же ось.
• 1. Скорость точки.
• Учитывая, что rx x,..ry y,..rz z , найдем:
dx
dy
dz
v
,
vy
, vz ,
x
dt
dt
dt
• или
vx x , v y y , , vz z .
• Модуль и направление скорости (углы , ,
• v образует с координатными осями):
v v x2 v y2 v z2
cos v x / v
,
cos v y / v
,
, которые вектор
cos vz / v
.
9. 9. Кинематика.
• 2. Ускорение точки.• Вектор ускорения:
• Отсюда:
dv d 2 r
a
2.
dt
dt
dv x d 2 x
ax
2 ,
dt
dt
d2y
ay
2 ,
dt
dt
dv y
dv z d 2 z
az
2 ,
dt
dt
• или ax v x x
, a y v y y
, az v z z .
• Проекции ускорения точки на координатные оси равны первым
производным от проекций скорости или вторым производным от
соответствующих координат точки по времени.
Модуль и направление ускорения ( 1 , 1 , 1 - углы, которые вектор
ускорения образует с координатными осями):
a a2 a2 a2 ;
x
y
z
cos 1 a x / a ; cos 1 a y / a
;
cos 1 a z / a .
10. 10. Кинематика.
• Скорость и ускорение точки при естественном задания движения• Даны траектория точки и закон движения точки вдоль траектории
s=f(t).
• Значения векторов v и a определяют по их проекциям на
подвижные оси M nb , которые движутся вместе с точкой М и
называются осями естественного трехгранника, или скоростными
осями.
Рис.41.
• Направление осей: ось M - по касательной к траектории в сторону
положительного отсчета расстояния s, ось Мn – по нормали к
траектории, лежащей в соприкасающейся плоскости и направленной в
сторону вогнутости траектории, ось Mb – перпендикулярно к осям M
и Mn так, чтобы она образовала с ними правую систему осей. Нормаль
Mn - главная нормаль, нормаль Mb – бинормаль.
11. 11. Кинематика. Скорость и ускорение точки при естественном задании движения.
• Поскольку вектор скорости точки совпадает с осью M , товеличина скорости определяется проекцией вектора на эту ось с
учетом знака v v
. Знак принято опускать и
называть v числовым (алгебраическим) значением скорости.
ds
v
s
dt
Числовое значение скорости точки в данный момент времени равно первой производной от расстояния
(криволинейной координаты) s этой точки по времени.
• Величина v определяет и модуль скорости, и ее направление – по знаку
модуля.
12. 12. Кинематика.
• Касательное и нормальное ускорение точки• Проекции вектора a d v на оси M , Mn, Mb: a d v / dt ,
dt
an d v n / dt ab 0
,
,
где
d v v v .
Рис.42.
• Касательное ускорение a характеризует изменение скорости по
величине и всегда направлено по касательной к траектории; при
ускорении движения тела направление a совпадает с направлением
вектора скорости, а при замедлении – противоположно направлению.
dv d 2 s
a
2
dt dt
13. 13. Кинематика. Касательное и нормальное ускорения точки
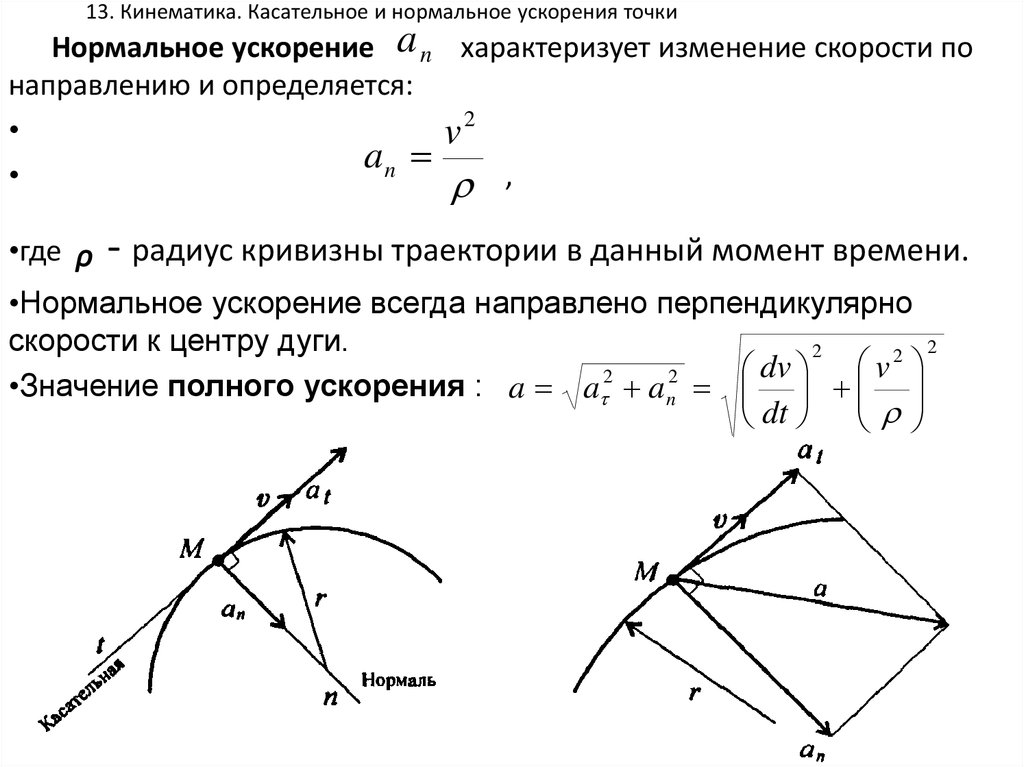
Нормальное ускорение a n характеризует изменение скорости понаправлению и определяется:
v2
an
,
•где
ᵨ - радиус кривизны траектории в данный момент времени.
•Нормальное ускорение всегда направлено перпендикулярно
скорости к центру дуги.
2
2 2
dv v
•Значение полного ускорения : a a 2 a n2
dt
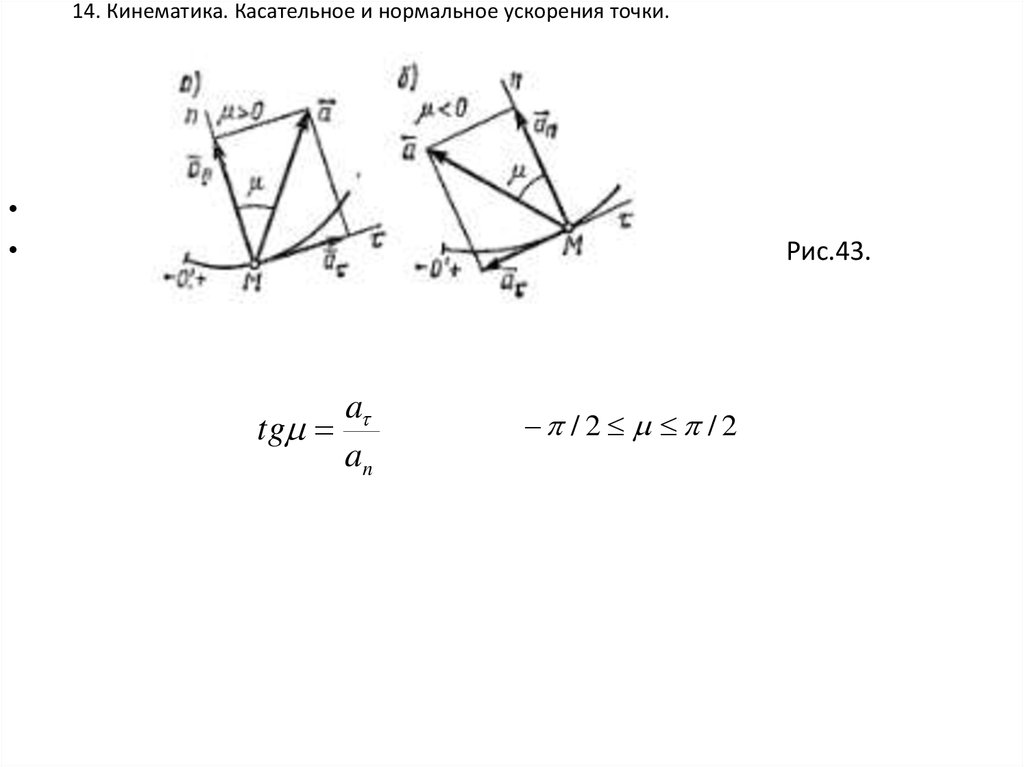
14. 14. Кинематика. Касательное и нормальное ускорения точки.
Рис.43.
a
tg
an
/ 2 / 2
15. 15. Кинематика.
• Частные случаи движения точки.• 1. Прямолинейное движение.
,
dv
v2
a
a
an
0
dt .
,
,
• Касательное ускорение характеризует изменение числового
значения скорости.
• 2.Равномерное криволинейное движение.
a
v2
dv
a an
0
,
.
dt
• V=сonst,
• Вектор a направлен по нормали к траектории точки.
• Нормальное ускорение характеризует изменение скорости по
направлению.
• Закон равномерного криволинейного движения:
ds
v
ds vdt
dt ,
,
При
s0 0
s
t
ds vdt
s0
s=vt, v=s/t.
0
,
s s0 vt
,
s s0 vt
.
16. 16. Кинематика. Частные случаи движения точки.
• 3. Равномерное прямолинейное движение.an a 0 , a 0 . Ускорение точки равно нулю только при
равномерном прямолинейном движении.
• 4. Равнопеременное криволинейное движение.
a const .
s 0 0 , v v0 .
• При t=0
dv
ds
a
v0 a t
, dv a dt . Интегрируем: v v0 a t . Или
dt
dt
ds v0 dt a tdt
.
• Интегрируем:
s s 0 v0 t a t 2 / 2
криволинейного движения точки.
- закон равнопеременного
17. 17. Кинематика. Поступательное движение.
• Кинематика твердого тела• Поступательное движение
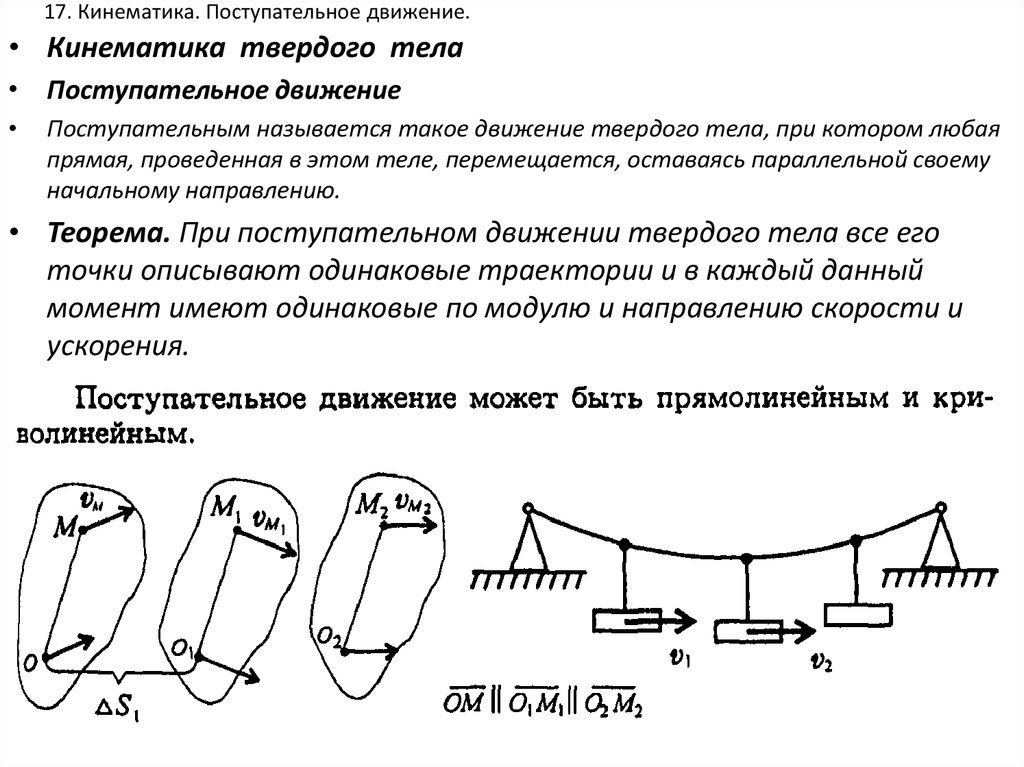
Поступательным называется такое движение твердого тела, при котором любая
прямая, проведенная в этом теле, перемещается, оставаясь параллельной своему
начальному направлению.
• Теорема. При поступательном движении твердого тела все его
точки описывают одинаковые траектории и в каждый данный
момент имеют одинаковые по модулю и направлению скорости и
ускорения.
18. 18. Кинематика. Поступательное движение
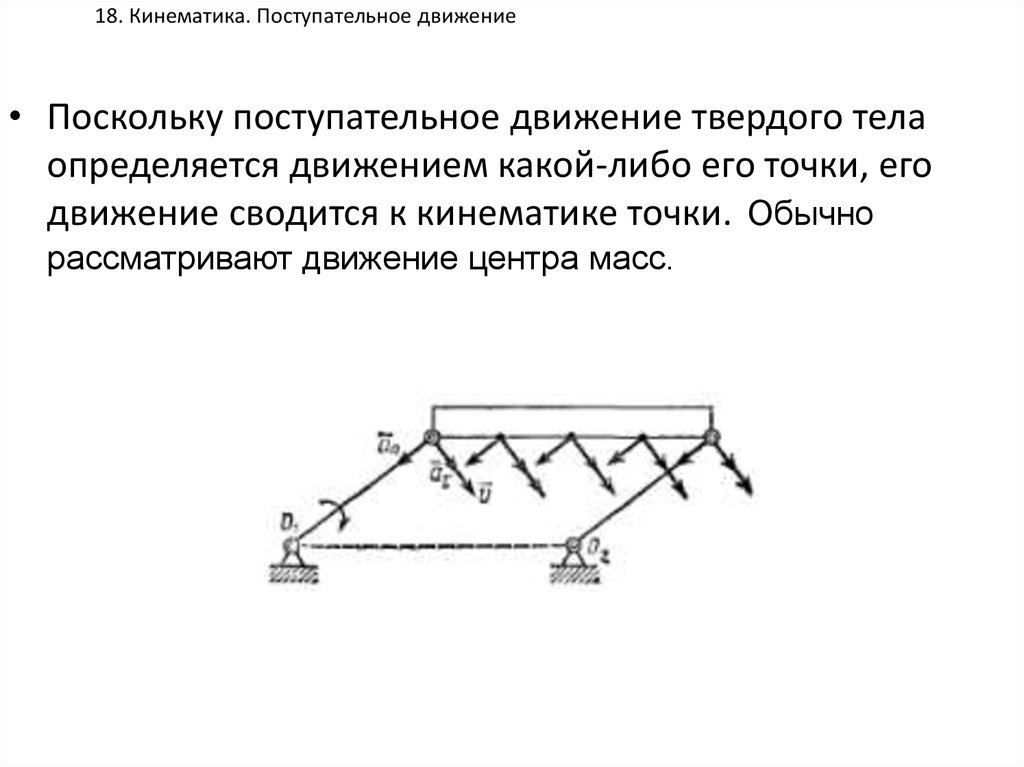
• Поскольку поступательное движение твердого телаопределяется движением какой-либо его точки, его
движение сводится к кинематике точки. Обычно
рассматривают движение центра масс.
19. 19. Кинематика.
• Вращательное движение твердого тела вокруг неподвижной оси.• Если твердое тело движется так, что две какие-нибудь его точки
остаются неподвижными, то такое движение называются
вращательным.
Неподвижная прямая АВ - ось вращения тела.
Каждая точка тела, не лежащая на оси вращения, описывает при таком вращении окружность, плоскость которой
перпендикулярность к оси вращения и центр которой
лежит на этой оси.
Для описания вращательного движения тела
вокруг неподвижной оси можно использовать
только угловые параметры.
Рис.48.
Вдоль оси вращения направим ось Az и проведем две полуплоскости: неподвижную – I,
- угол поворота тела. Считаем, что положителен,
и подвижную – II.
если он отложен от неподвижной плоскости в направлении против хода часовой
стрелки, если смотреть с положительного конца оси Az.
[ ] = рад.
• Положение тела в любой момент времени определяется углом , закон
вращательного движения твердого тела вокруг неподвижной оси:
.
f t
20. 20. Кинематика. Вращательное движение.
dопределяется:
или .
dt
20. Кинематика. Вращательное движение.
• Угловая скорость тела
• Таким образом, числовое значение угловой скорости тела в данный момент
времени равно первой производной от угла поворота по времени.
• Размерность – 1/T, рад/сек=1/сек= сек 1 .
• Угловое ускорение характеризует изменение угловой скорости тела с
течением времени.
d d 2
2
dt
dt
или
.
• Числовое значение углового ускорения тела в данный момент времени
равно первой производной от угловой скорости или второй производной от
угла поворота тела по времени.
• Размерность – 1/ T 2 , 1/ с 2 сек 2 .
21. 21. Кинематика.
• Равномерное вращениеУгловая скорость постоянна, т.е.
0 t
= const .
s s0 vt
- закон
равном. кривол. дв-я
• Равнопеременное вращение
Угловое ускорение тела постоянно, т.е.
0 0 t
t 2
= const .
2
Если величины
и
имеют одинаковые знаки, то вращение будет
равноускоренным, а если имеют разные знаки – равнозамедленным.
s s 0 v0 t a t 2 / 2
- з-н равноперем. кривол.
дв-я точки.
22. 22. Кинематика.
• Определение скоростей и ускорений точек вращающегосятела
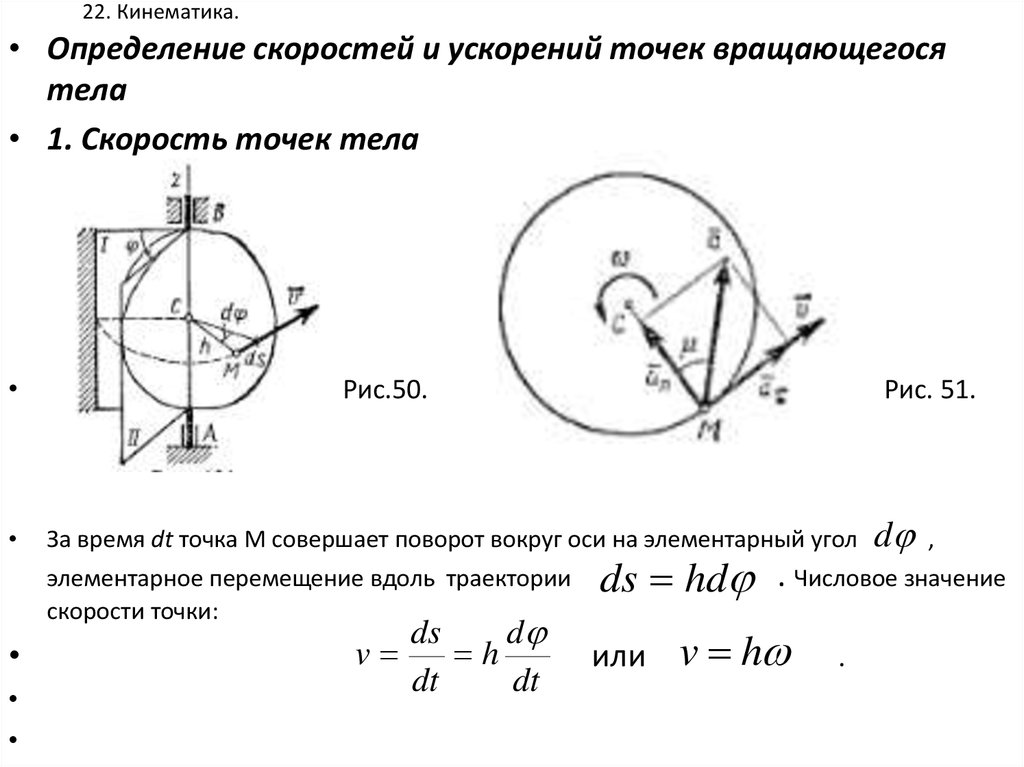
• 1. Скорость точек тела
Рис.50.
За время dt точка М совершает поворот вокруг оси на элементарный угол
элементарное перемещение вдоль траектории
скорости точки:
Рис. 51.
ds
d
v
h
dt
dt
d
,
ds hd . Числовое значение
или
v h
.
23. 23. Кинематика. Скорость точек твердого тела при вращательном движении.
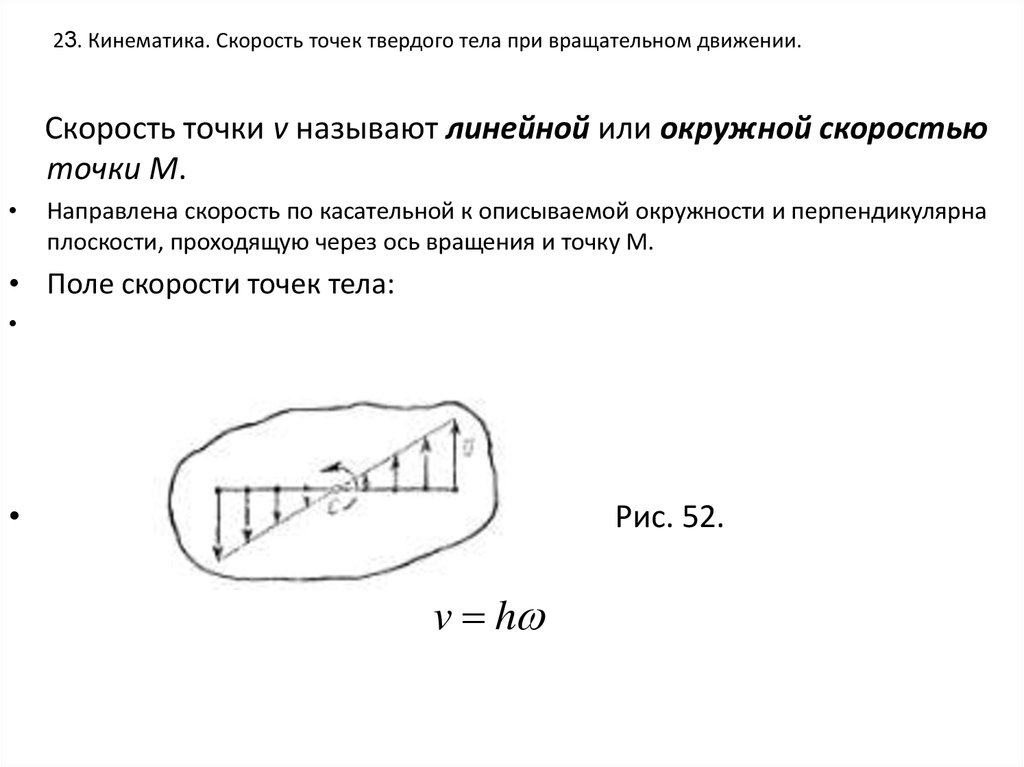
Скорость точки v называют линейной или окружной скоростьюточки М.
Направлена скорость по касательной к описываемой окружности и перпендикулярна
плоскости, проходящую через ось вращения и точку М.
• Поле скорости точек тела:
Рис. 52.
v h
24. 24. кинематика. Вращательное движение твердого тела.
• 2.Ускорение точек тела.Воспользуемся формулами: a dv
dt
2 2
d
h
• Тогда, a h
, a
.
n
dt
h
2
a
h
a
h
• Или
, n
.
• Полное ускорение
2
v
, a
,
n
h
.
v h
a a 2 a n2 или a h 2 2 .
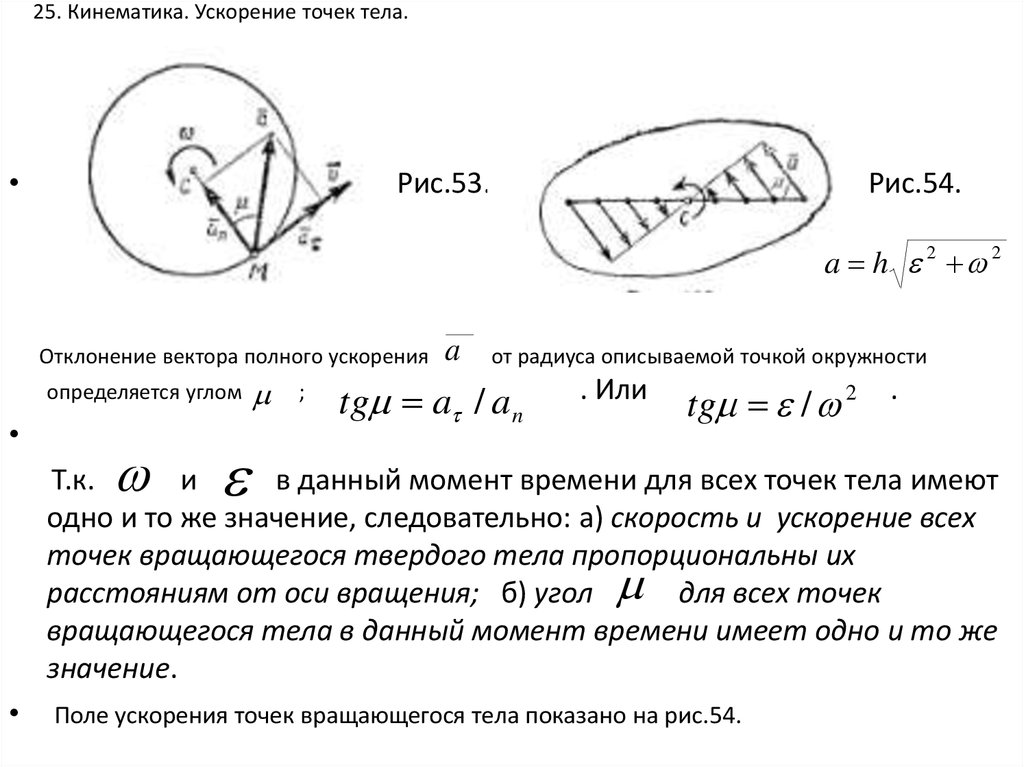
25. 25. Кинематика. Ускорение точек тела.
Рис.53.
Рис.54.
a h 2 2
Отклонение вектора полного ускорения
определяется углом
;
a
от радиуса описываемой точкой окружности
tg a / a n
. Или
tg / 2 .
Т.к.
и
в данный момент времени для всех точек тела имеют
одно и то же значение, следовательно: а) скорость и ускорение всех
точек вращающегося твердого тела пропорциональны их
расстояниям от оси вращения; б) угол для всех точек
вращающегося тела в данный момент времени имеет одно и то же
значение.
Поле ускорения точек вращающегося тела показано на рис.54.
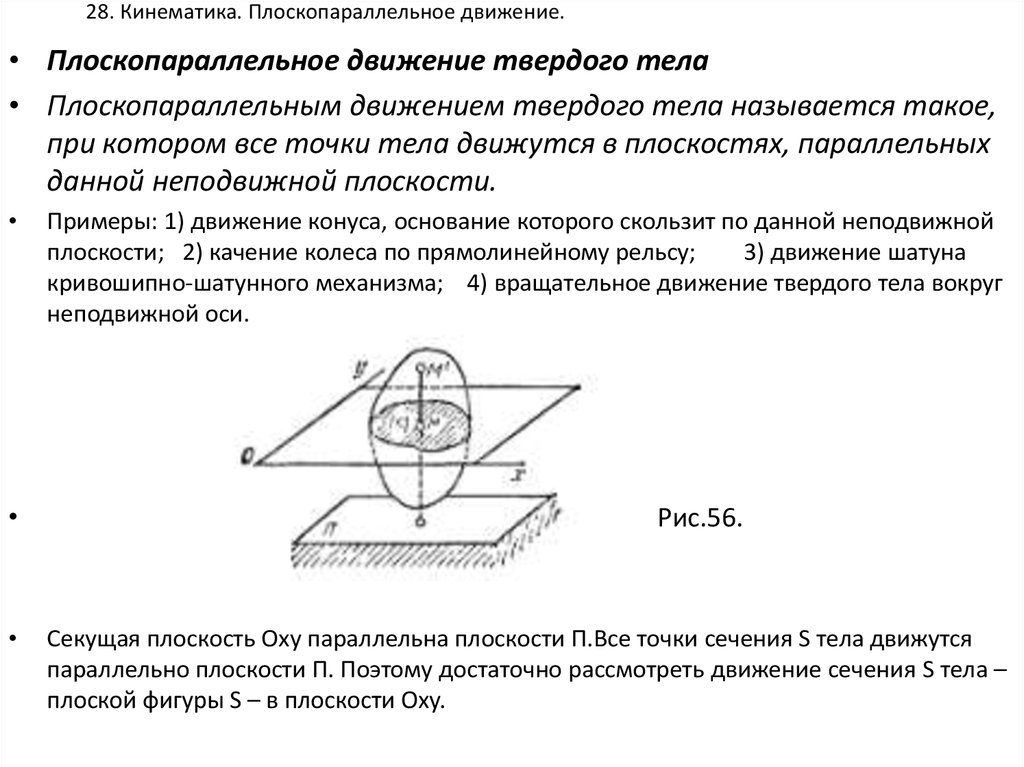
26. 28. Кинематика. Плоскопараллельное движение.
• Плоскопараллельное движение твердого тела• Плоскопараллельным движением твердого тела называется такое,
при котором все точки тела движутся в плоскостях, параллельных
данной неподвижной плоскости.
Примеры: 1) движение конуса, основание которого скользит по данной неподвижной
плоскости; 2) качение колеса по прямолинейному рельсу;
3) движение шатуна
кривошипно-шатунного механизма; 4) вращательное движение твердого тела вокруг
неподвижной оси.
Рис.56.
Секущая плоскость Оxy параллельна плоскости П.Все точки сечения S тела движутся
параллельно плоскости П. Поэтому достаточно рассмотреть движение сечения S тела –
плоской фигуры S – в плоскости Oxy.
27. 29. Кинематика. Плоскопараллельное движение твердого тела.
На плоскости сечения S проведем отрезок АВ, который и будет определять положение
плоской фигуры S.
Положение отрезка определяется координатами
и углом (с осью x). Точку А назовем полюсом.
xA , yA
Рис. 57.
x A f1 t y A f 2 t
,
,
f 3 t
- уравнения
плоскопараллельного движения твердого тела.
Первые два уравнения – уравнения поступательного движения. Третье уравнение определяет движение, которое совершила бы фигура S при неподвижном
полюсе А. Следовательно
,
Движение плоской фигуры в общем случае можно разложить на два
движения: 1) поступательное движение со скоростью, равной
скорости произвольно выбранной точки фигуры (полюса);
2) вращательное движение вокруг этой точки.
28. 30. Кинематика. Плоскопараллельное движение.
• Основные кинематические характеристики этогодвижения являются: 1) скорость и ускорение
поступательного движения, равные скорости и
ускорению полюса (
a пост a A ), и
v пост v A ,
2) угловая скорость и угловое ускорение
вращательного движения вокруг полюса.
• Вращательная часть движения не зависит от
выбора полюса.
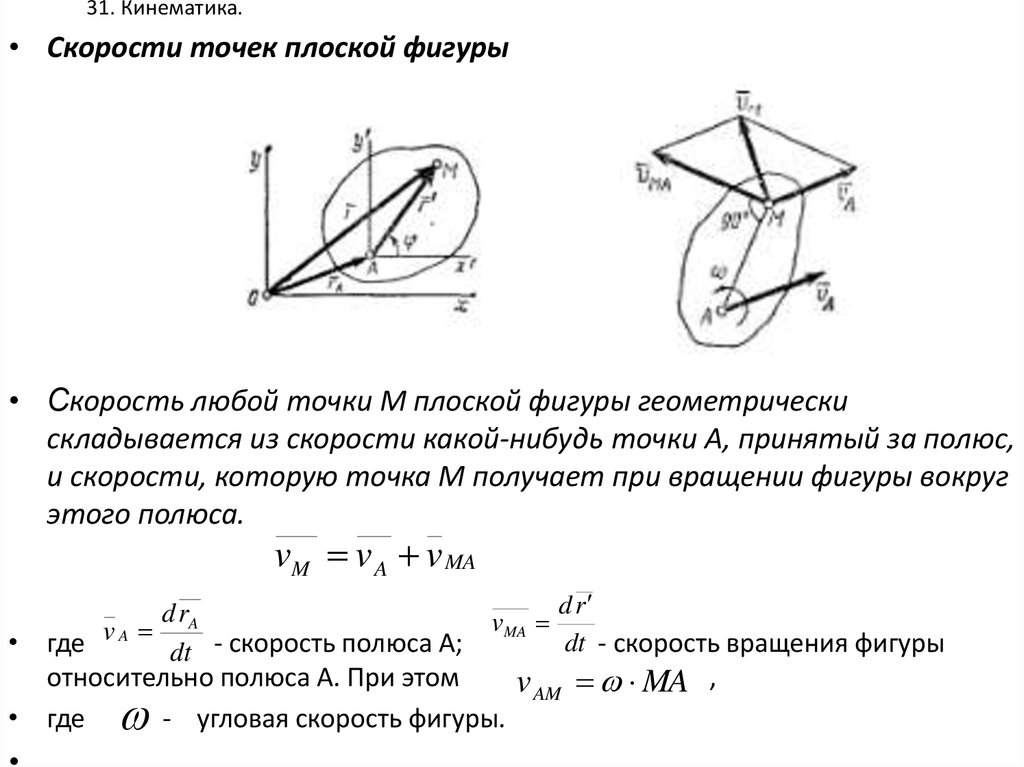
29. 31. Кинематика.
• Скорости точек плоской фигуры• Скорость любой точки М плоской фигуры геометрически
складывается из скорости какой-нибудь точки А, принятый за полюс,
и скорости, которую точка М получает при вращении фигуры вокруг
этого полюса.
vM v A v MA
d rA
v
A
где
dt - скорость полюса А;
vMA
d r
dt - скорость вращения фигуры
относительно полюса А. При этом
v AM MA ,
• где
- угловая скорость фигуры.
30. 32. Кинематика.
• Ускорение точек плоской фигурыУскорение каждой точки движущейся плоской фигуры равно
геометрической сумме двух ускорений: 1) ускорения в
поступательном (переносном) движении полюса и 2) ускорения во
вращательном движении вокруг полюса (в относительном
движении).
aM a A a MA
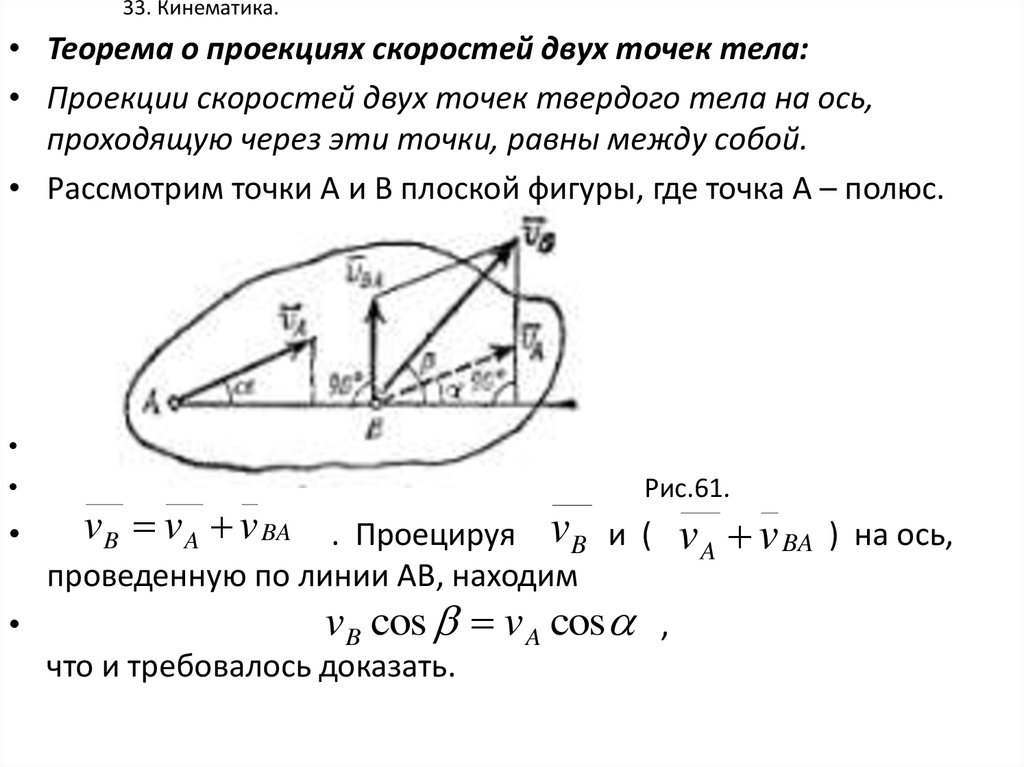
31. 33. Кинематика.
• Теорема о проекциях скоростей двух точек тела:• Проекции скоростей двух точек твердого тела на ось,
проходящую через эти точки, равны между собой.
• Рассмотрим точки А и В плоской фигуры, где точка А – полюс.
Рис.61.
vB v A v BA . Проецируя v B и ( v v BA ) на ось,
A
проведенную по линии АВ, находим
vB cos v A cos ,
что и требовалось доказать.
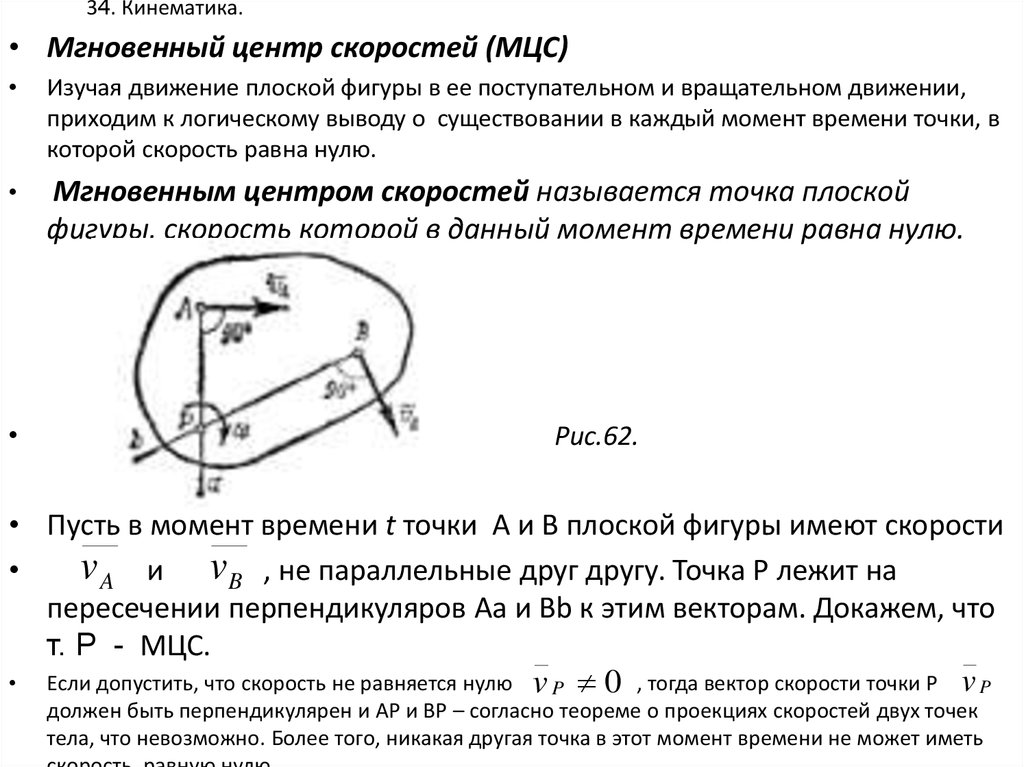
32. 34. Кинематика.
• Мгновенный центр скоростей (МЦС)Изучая движение плоской фигуры в ее поступательном и вращательном движении,
приходим к логическому выводу о существовании в каждый момент времени точки, в
которой скорость равна нулю.
Мгновенным центром скоростей называется точка плоской
фигуры, скорость которой в данный момент времени равна нулю.
Рис.62.
• Пусть в момент времени t точки А и В плоской фигуры имеют скорости
v A и vB , не параллельные друг другу. Точка Р лежит на
пересечении перпендикуляров Aa и Вb к этим векторам. Докажем, что
т. Р - МЦС.
• Если допустить, что скорость не равняется нулю v P 0 , тогда вектор скорости точки Р v P
должен быть перпендикулярен и АР и ВР – согласно теореме о проекциях скоростей двух точек
тела, что невозможно. Более того, никакая другая точка в этот момент времени не может иметь
33. 35. Кинематика. МЦС.
• Если Р - полюс, то скорость, например, точки А в момент времени t:v v v
v
PA
PA
A
P
,
• т.к. v P 0 . Следовательно, скорости точек плоской фигуры
определяются в данный момент времени так, как если бы движение
фигуры было вращением вокруг МЦС.
• Покажем, что скорости точек плоской фигуры пропорциональны их
расстояниям от МЦС.
v A PA ;
vB PB
; следовательно, v A v B .
PA PB
34. 36. Кинематика. МЦС.
• Выводы:• 1. Для определения МЦС надо знать только направления
скоростей v и v
двух точек А и В плоской фигуры.
A
B
• 2. МЦС лежит в точке пересечения перпендикуляров,
восстановленных в двух точках фигуры к скоростям этих
точек.
• 3. Для определения скорости любой точки плоской фигуры надо
знать модуль и направление скорости какой-нибудь одной
точки А фигуры и направление скорости другой ее точки В.
• 4. Угловая скорость плоской фигуры равна в каждый
данный момент времени отношению скорости какой-нибудь
точки фигуры к ее расстоянию от МЦС (т. Р):
vB
PB
.
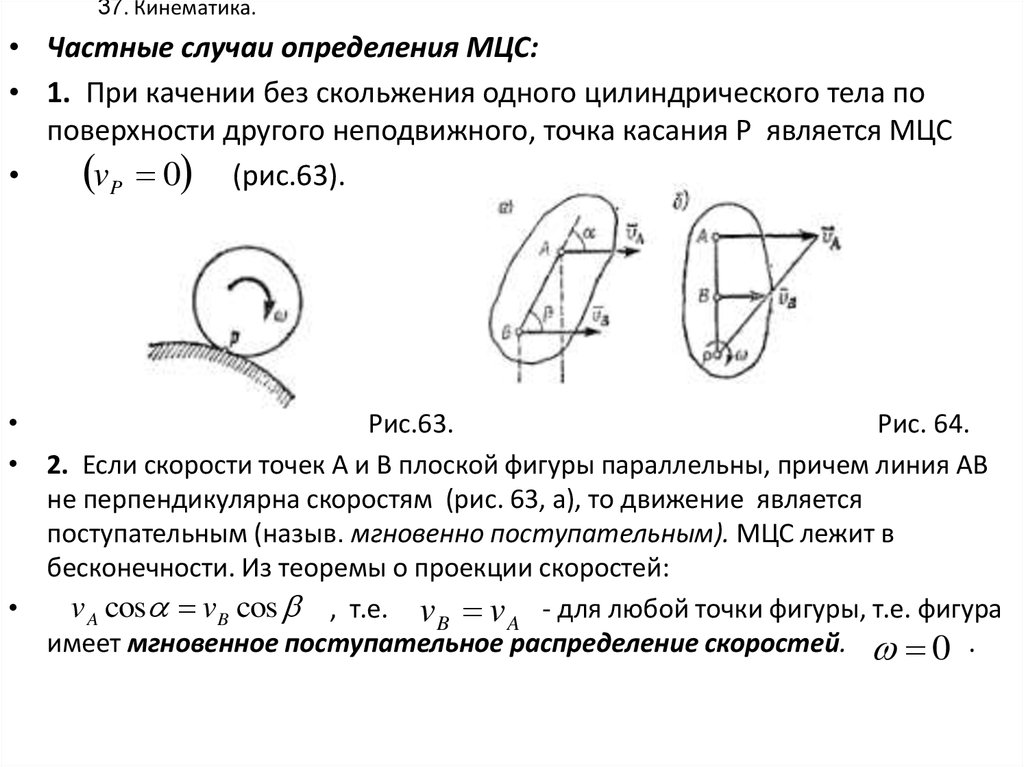
35. 37. Кинематика.
• Частные случаи определения МЦС:• 1. При качении без скольжения одного цилиндрического тела по
поверхности другого неподвижного, точка касания Р является МЦС
vP 0 (рис.63).
Рис.63.
Рис. 64.
• 2. Если скорости точек А и В плоской фигуры параллельны, причем линия АВ
не перпендикулярна скоростям (рис. 63, а), то движение является
поступательным (назыв. мгновенно поступательным). МЦС лежит в
бесконечности. Из теоремы о проекции скоростей:
v A cos vB cos , т.е. v B v A - для любой точки фигуры, т.е. фигура
имеет мгновенное поступательное распределение скоростей. 0 .
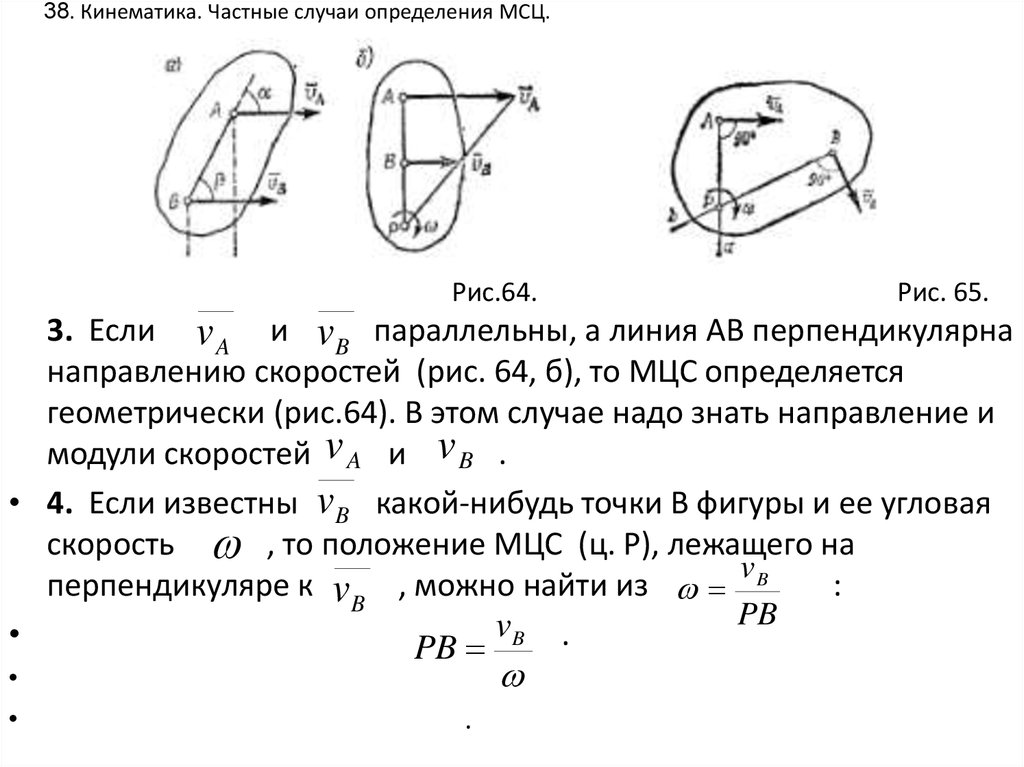
36. 38. Кинематика. Частные случаи определения МСЦ.
Рис.64.Рис. 65.
3. Если v A и v B параллельны, а линия АВ перпендикулярна
направлению скоростей (рис. 64, б), то МЦС определяется
геометрически (рис.64). В этом случае надо знать направление и
модули скоростей v A и v B .
• 4. Если известны v B какой-нибудь точки В фигуры и ее угловая
скорость , то положение МЦС (ц. Р), лежащего на
v
перпендикуляре к v B , можно найти из B
:
PB
v
PB B .
.





















 Физика
Физика








