Похожие презентации:
Определители. Свойства определителей
1. Определители. Свойства определителей.
2.
• Определителем(детерминантом)
матрицы n-го порядка называется число:
a11
a 21
n det A
...
a n1
a12
a 22
...
an 2
... a1n
... a 2 n
... ...
... a nn
3.
a11 a122
a11a22 a12a21
a21 a22
2
4.
a113 a 21
a31
a12
a 22
a32
a13
a 23 a11a 22 a33 a 21a32 a13 a12 a 23 a31
a33
a13 a 22 a31 a32 a23 a11 a21a12 a33
5.
• Правило Сарруса:a11 a12
a21 a22
a31 a32
a13
a23
a33
a11 a12
a21 a22
a31 a32
a11a22a33 a12a23a31 a13a21a32
a13a22a31 a11a23a32 a12a21a33
6.
a113 a 21
a31
a12
a 22
a32
a13
a 23 a11a 22 a33 a 21a32 a13 a12 a 23 a31
a33
a a a a a a a a a
13 22 31
• Правило треугольника:
«+»
«-»
32 23 11
21 12 33
7.
Примеры:1)
3 2
3 5 2 1 15 ( 2) 17
1 5
2)
cos x sin x
cos 2 x sin 2 x cos 2 x
sin x cos x
3)
cos x sin x
2
2
cos x sin x 1
sin x cos x
8.
Примеры:4)
log 2 32 log 3 27
log 4 16 log 5 125
5 3
15 6 9
2 3
9.
Примеры:5)
4 7 2 4 7
3 1 5 3 1
5 0
7 5 0
4 ( 1) 7 7 5 5 ( 2) 3 0
5 ( 1) ( 2) 0 5 4 7 3 7
28 175 0 10 0 147 10
10. Свойства определителей.
1.Определитель не изменится, если егоT
транспонировать:
det A det A
3 5
det A
12 10 22
2 4
3 2
det A
12 10 22
5 4
T
11.
2.При перестановке двух строк илистолбцов определитель изменит свой
знак на противоположный.
3 5
12 10 22
2 4
2 4
10 12 22
3 5
12.
3. Общий множитель всех элементовстроки или столбца можно вынести за
знак определителя.
a11 ka12
a11 a12
k
a21 ka22
a21 a22
13.
12
2
1 2 2
1 2 1
36 12 24 12 3 1 2 12 2 3 1 1
1 3 4
1 3 4
1 3 2
24 2 9 2 1 12 3 24 15 360
14.
4. Определитель с двумя одинаковымистроками или столбцами равен нулю.
1 1 3
1 1 3
2 1 4
4 3 6 6 3 4 0
15.
5. Если все элементы двух строк (илистолбцов) определителя пропорциональны,
то определитель равен нулю.
3 7 1
3 7 1
2 3 1 2 2 3 1 2 0 0
2 3 1
4 6 2
16.
6. Если каждый элемент какого-либо рядаопределителя представляет собой сумму
двух слагаемых, то такой определитель
равен сумме двух определителей, в первом
из которых соответствующий ряд состоит из
первых слагаемых, а во втором- из вторых
слагаемых.
17.
a11a21
...
an1
a11
a21
...
an1
... a1 j
... a2 j
... ...
... anj
... a1 j b1 j
... a2 j b2 j
...
...
... anj bnj
... a1n
... a2 n
... ...
... ann
... a1n
a11
... a2 n
a21
... ...
...
... ann
an1
... b1 j
... b2 j
... ...
... bnj
... a1n
... a2 n
... ...
... ann
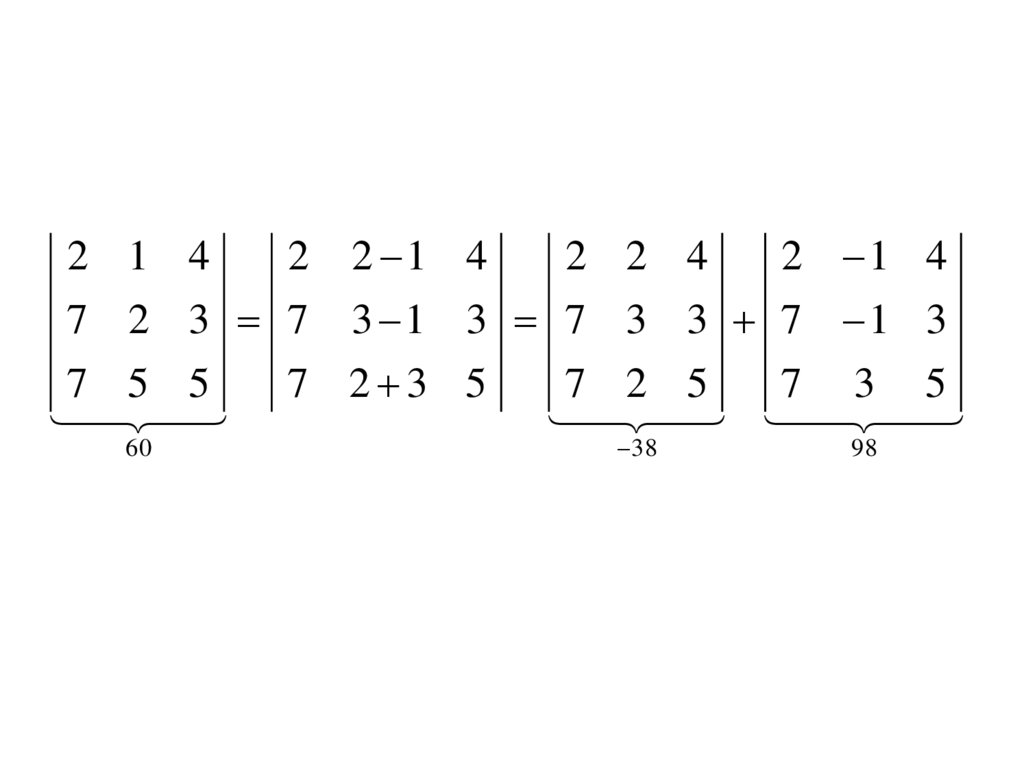
18.
2 1 42 2 1 4
2 2 4
2 1 4
7 2 3 7 3 1 3 7 3 3 7 1 3
7 5 5
7 2 3 5
7 2 5
7 3 5
60
38
98
19.
7. Если к какой-либо строке (или столбцу)определителя прибавить соответствующие
элементы другой строки (или столбца) ,
умноженные на одно и то же число, то
определитель не изменится.
a11 a12
a21 a22
к
×
a11
a12
ka11 a21 ka12 a22
20.
5 110 0 10
0 2
5 1 ×2
5 1
0 10 10
+
0 2
10 0
21.
8.Треугольный
произведению
диагонали.
a11 0
a21 a22
a31 a32
определитель
равен
элементов
главной
0
a11 a12
0 0 a22
a33
0
0
a13
a23 a11 a22 a33
a33
22. Привести определитель к треугольному виду и вычислить его:
2 1 41 2 4 ×(-2) ×(-5)
7 2 3 2 7 3
7 5 5
5 7 5
1 2
4
0 3 5
0 3 15
=
1 2
4
0 3 5 60
+
0 0 20
23. Разложение определителя по элементам строки или столбца.
• Минором Mij элемента aij det Dназывается такой новый определитель,
который
получается
из
данного
вычеркиванием i-ой строки и j-го
столбца содержащих данный элемент.
24.
a11 a12det D a21 a22
a31 a32
a13
a23
a33
a21 a23
M12
a31 a33
a11 a12
det D a21 a22
a31 a32
a13
a23
a33
a11 a12
M 23
a31 a32
25. Для данного определителя найти миноры: М22, М31,М43
1 23
0 1 5
3 2 1
1 1 3
4
2
4
2
2
3 4
M 31 1 5 2 36
1 3 2
1 3 4
M 22 3 1 4 28
1 3 2
1 2 4
M 43 0 1 2 16
3 2 4
26.
• Алгебраическимдополнением
Aij
элемента aij det D называется минор Mij
этого элемента, взятый со знаком 1 i j
т.е.
Aij 1
i j
M ij
27.
Aij 1i j
a11 a12
det D a21 a22
a31 a32
a13
a23
a33
M ij
a21 a23
M 12 1
a31 a33
A12 1
1 2
A22 1
2 2
a11 a13
M 22
a31 a33
28.
• Сумма произведений элементов любойстроки (или столбца) определителя на их
алгебраические дополнения равна этому
определителю.
29.
разложение по i-ой строке:n
det D ai1 Ai1 ai 2 Ai 2 ... ain Ain aik Aik , i 1,..., n
k 1
разложение по j-му столбцу:
n
det D a1 j A1 j a2 j A2 j ... anj Anj akj Akj ,
k 1
j 1,..., n
30. Разложить данный определитель по элементам: 1) 3-ей строки; 2) 1-го столбца.
1 23
0 1 5
3 2 1
1 1 3
4
2
4
2
31. 1) Разложим данный определитель по элементам 3-ей строки:
1) Разложим данныйэлементам 3-ей строки:
определитель
по
det D a31 A31 a32 A32 a33 A33 a34 A34
a31 1 M 31 a32 1 M 32
4
5
a33 1 M 33 a34 1 M 34
6
7
32.
23 4
1 3 4
4
5
3 1 1 5 2 2 1 0 5 2
1 3 2
1 3 2
1 2 4
1 2
3
6
7
1 1 0 1 2 4 1 0 1 5
1 1 2
1 1 3
3 36 2 2 4 4 11 56
33. 2) Разложим данный определитель по элементам 1-го столбца:
2) Разложим данныйэлементам 1-го столбца:
определитель
по
det D a11 A11 a21 A21 a31 A31 a41 A41
a11 1 M 11 a21 1 M 21
2
3
a31 1 M 31 a41 1 M 41
4
5
34.
1 5 22 3 4
2
3
1 1 2 1 4 0 1 2 1 4
1 3 2
1 3 2
2
3 4
2 3 4
4
5
3 1 1 5 2 1 1 1 5 2
1 3 2
2 1 4
20 0 3 36 32 56
35. Основные методы вычисления определителя.
1. разложение определителя поэлементам строки или столбца;
2. метод эффективного понижения
порядка;
3. приведение определителя к
треугольному виду.
36.
Метод эффективного понижения порядка:Вычисление определителя n-го порядка
сводится
к
вычислению
одного
определителя (n-1)-го порядка, сделав в
каком-либо ряду все элементы, кроме
одного, равными нулю.
37.
1 23
0 1 5
3 2 1
1 1 3
4 ×(-3) ×(-1)
2
4
2
1 2
3
4
0 1 5
2
0 4 10 8
0 1 6 2
38.
1 23
4
1 2
0 1 5
2
0 1
2
2 2 1
0 2
5
4
0 2
0 1 6 2
0 1
1 5 1
2
4 1 1 2 5 2 4 14 56
1 6 1
3
5
5
6
2
1
2
1
39. Вычислить определитель приведением его к треугольному виду.
1 23
0 1 5
3 2 1
1 1 3
4 ×(-3) ×(-1)
2
4
2
1 2
3
4
0 1 5
2
0 4 10 8
0 1 6 2
40.
1 23
4
1 2
0 1 5
2
0 1
2
2 2 1
0 2
5
4
0 2
0 1 6 2
0 1
1 2
0 1
4
0 2
0 1
3
5
5
6
2
1 ×2
2
+
1
3
5
5
6
2
1
2
1
1 2 3 2
0 1 5 1
4
0 0 15 4
0 0 11 2
41.
1 20 1
4
0 0
0 0
2 3
1 5
4 15
2 11
1 2
0 1
4
0 0
0 0
1 2
0 1
4
0 0
0 0
2 3
1 5
4 14 56
2 11
0 7
2 3
1 5
2 11 ×(-2)
4 15


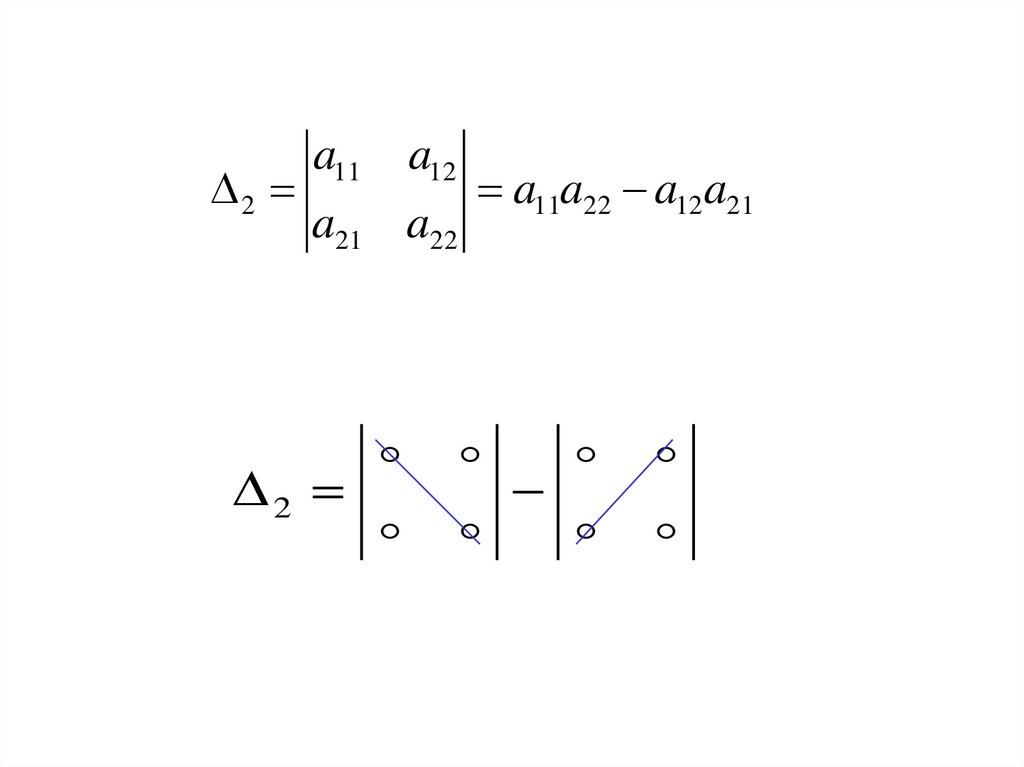




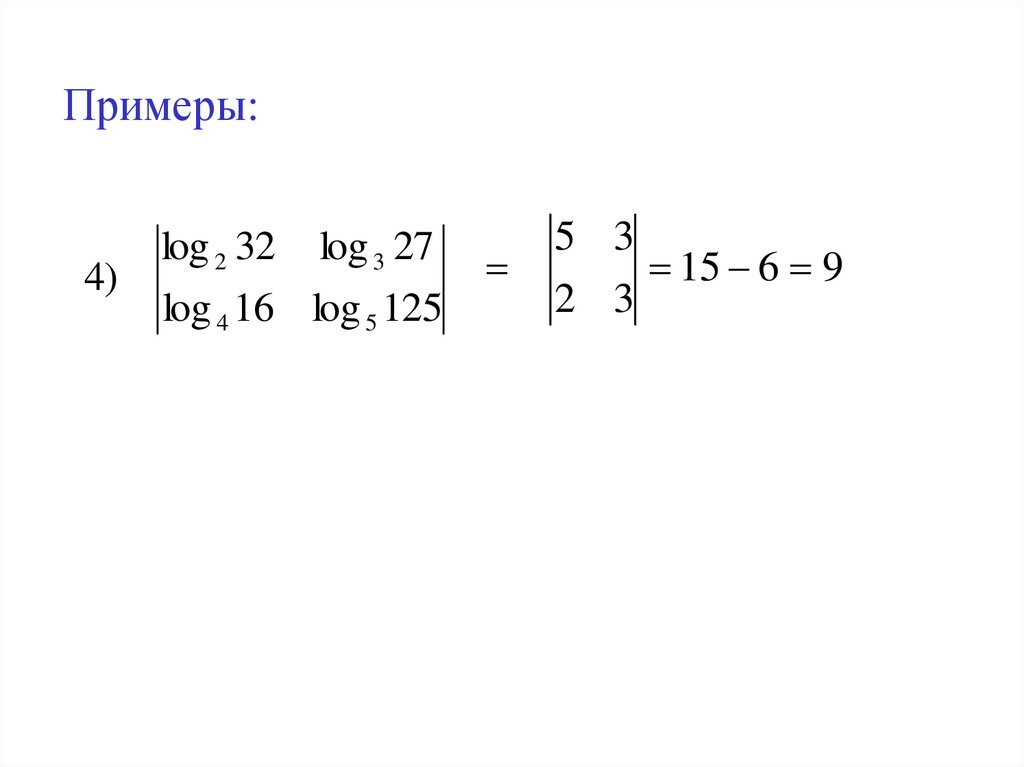

















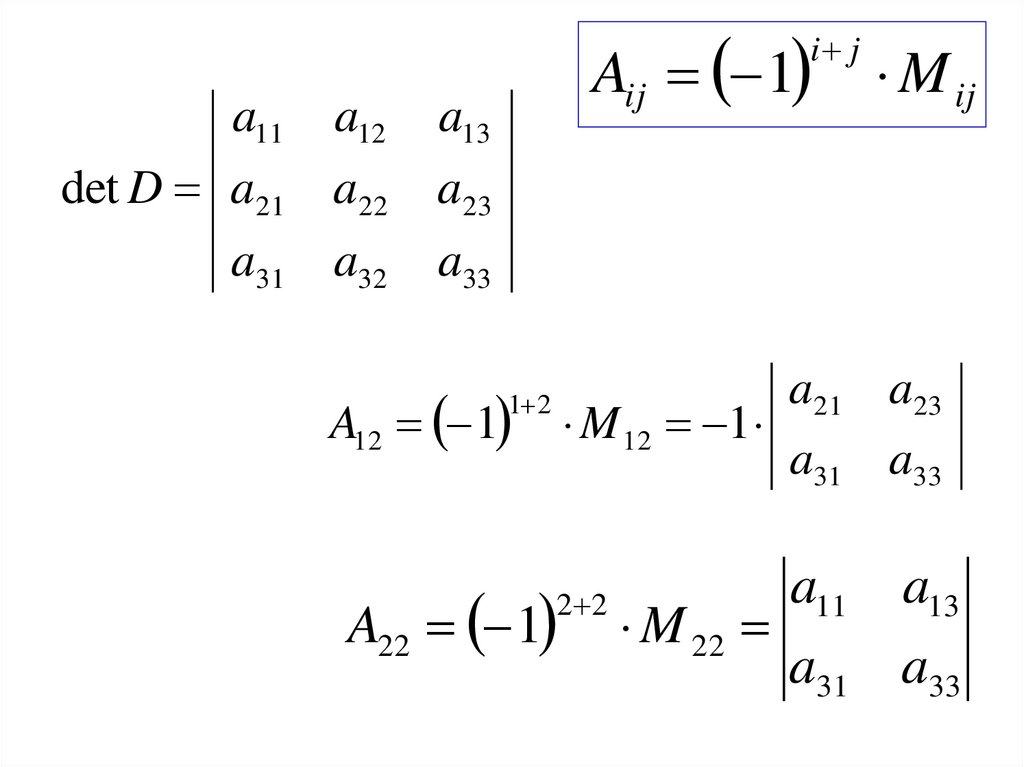










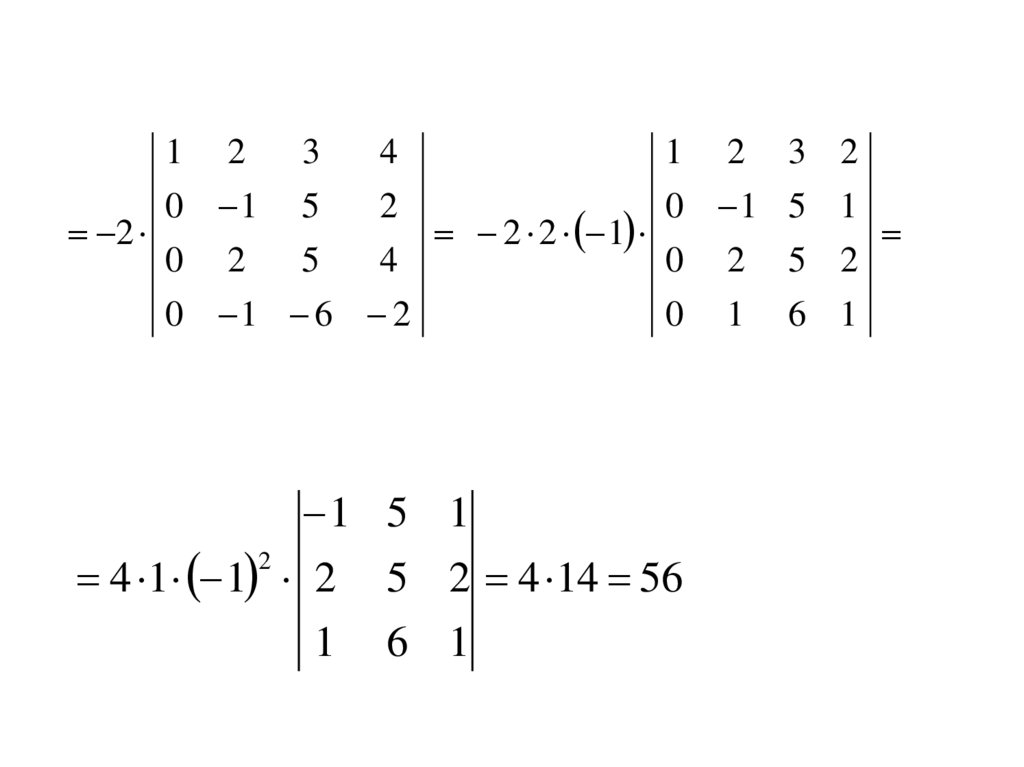



 Математика
Математика








