Похожие презентации:
Неопределённый интеграл
1. Неопределённый интеграл
Все записать решить сфотографироватьи выслать на почту Korotkova681@mail.ru
2.
Задача интегрального исчисления:найти
функцию,
зная
её
производную.
• Функция F(x) называется первообразной для
функции f(x) на заданном промежутке, если
для любого х из этого промежутка справедливо
равенство Fʹ(x) = f(x).
3. Неопределённый интеграл.
Множество всех первообразных F(x)+C
функции f(x) на некотором промежутке
называется неопределённым интегралом и
обозначается символом f ( x)dx , т.е
f ( x) dx F ( x) C
4.
f ( x) dx F ( x) Cf (x ) - подынтегральная функция
f ( x) dx - подынтегральное выражение
х – переменная интегрирования
- знак неопределённого интеграла
F(x)+C – множество всех первообразных
С – постоянная интегрирования
Процесс нахождения первообразной функции называется
интегрированием, а раздел математики- интегральным
исчислением.
5. Свойства неопределённого интеграла.
• 1. Дифференциал от неопределённогоинтеграла
равен
подынтегральному
выражению, а производная неопределённого
интеграла равна подынтегральной функции:
d f ( x) dx f ( x) dx,
f ( x) dx f ( x)
6.
• 2.Неопределённый
интеграл
от
дифференциала некоторой функции равен этой
функции плюс произвольная постоянная, т.е
d F ( x) F ( x) C
7.
• 3.Неопределённый
интеграл
от
алгебраической суммы двух или нескольких
функций равен алгебраической сумме их
интегралов, т.е
f ( x) g ( x) dx f ( x) dx g ( x) dx
8.
• 4. Постоянный множитель можно выносить зазнак интеграла, т.е
a f ( x) dx a f ( x) dx , a 0
9. Таблица интегралов.
1)0dx C , C const
n 1
x
2) x dx
C , n 1
n 1
n
dx x C
dx
3)
ln x C
x
10.
xa
4) a dx
C , a 0, a 1
ln a
x
5)
cos
xdx
sin
x
C
e
dx
e
C
x
6)
x
sin
xdx
cos
x
C
11. Пример . Вычислить интеграл
2 x 3sin x 5e dx4
x
2 x 3sin x 5e dx 2 x dx 3sin x dx 5e dx
4
x
2 5
x
x 3 cos x 5e C ,
5
4
x
C C1 C 2 C3
12. . Вычислить интеграл
2 xx dx
4
.
Вычислить интеграл









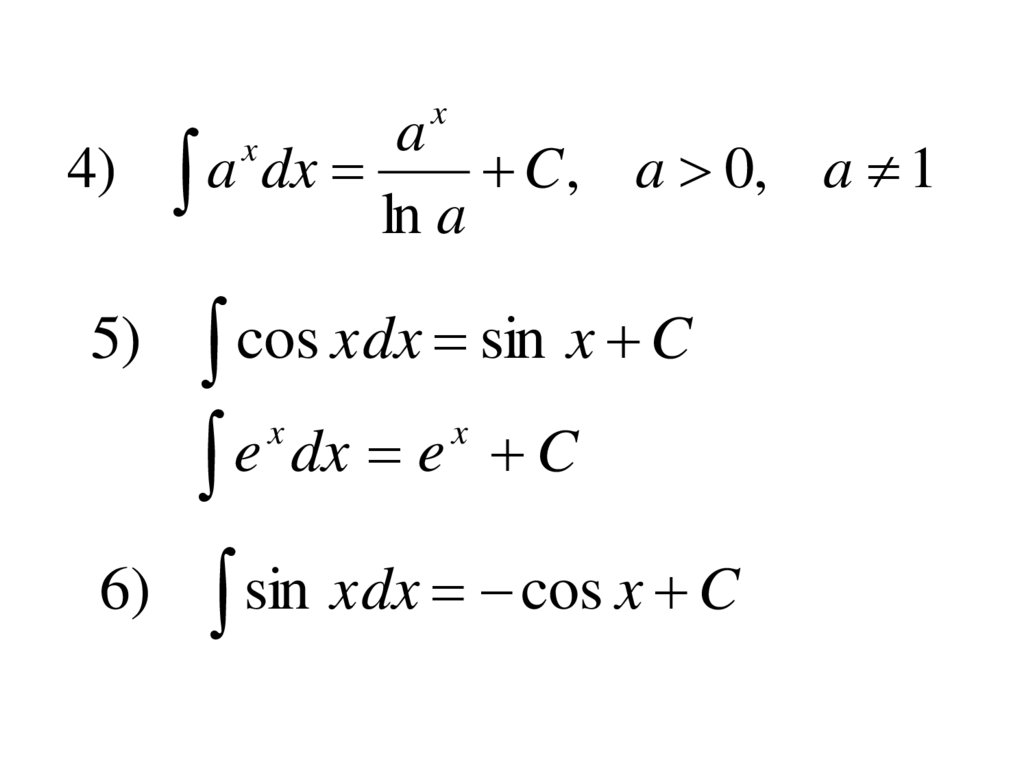
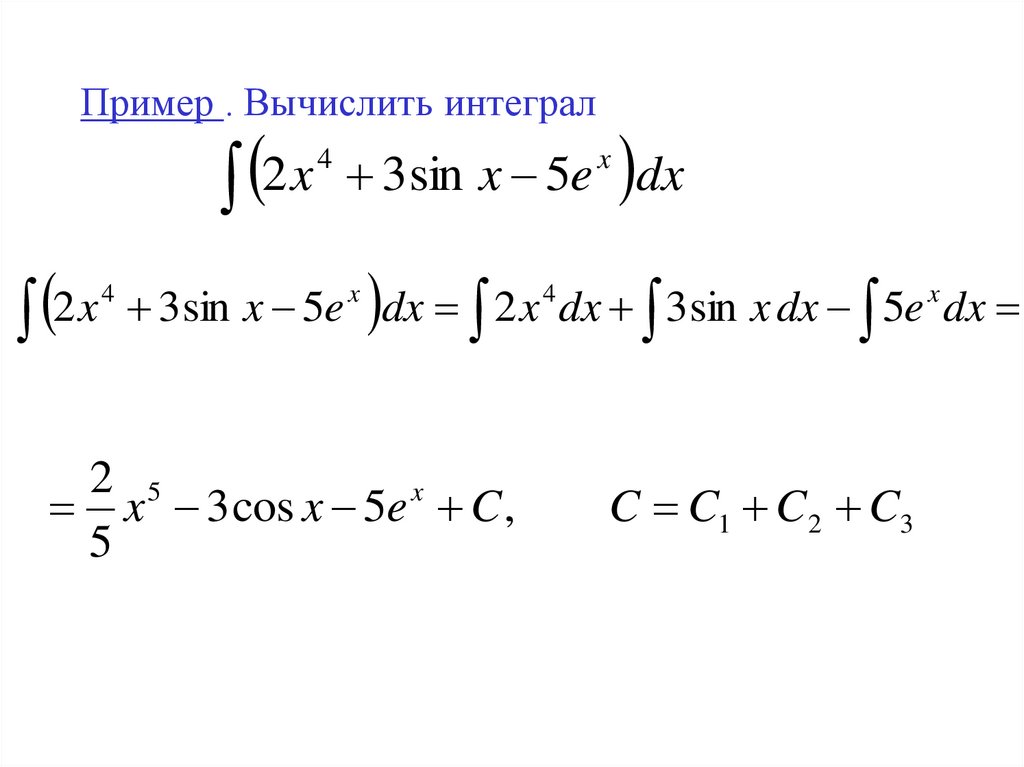

 Математика
Математика








