Похожие презентации:
Неопределённый интеграл, его свойства . Непосредственное интегрирование. Метод замены переменной в неопределенном интеграле
1. Математика ППИ
Лекция 11.Неопределённый интеграл, его свойства .
Непосредственное интегрирование. Метод
замены переменной в неопределенном
интеграле. Интегрирование функций,
содержащих квадратный трехчлен
2. Математика ППИ
Лекция 11.Неопределённый интеграл . Методы
интегрирования: замена переменной.
3. Цели и задачи:
Дать понятие первообразной инеопределенного интеграла.
Изучить основные свойства
интеграла.
4. Цели и задачи:
Изучить основные методыинтегрирования:
интегрирование методом замены
переменной, по частям.
5. Вопросы лекции
1. Первообразная инеопределенный интеграл.
2. Основные свойства
неопределённого интегра.
3.Интегрирование
разложением, внесением под
знак дифференциала.
4. Метод замены переменной в
неопределенном интеграле.
Интегрирование функций,
содержащих квадратный
трехчлен.
6. ЛИТЕРАТУРА
[1] Н.С. Пискунов. Дифференциальноеи интегральное исчисления. Т 1.
Москва: Интеграл-Пресс, 2004. с. 340375;
[3] Б.П. Демидович, В.А. Кудрявцев.
Краткий курс высшей математики.
Москва: Издательство АСТ, 2004.. с.
229-275;
7.
Интеграл (от лат. integer — целый), одноиз важнейших понятий математики. Оно
возникло в связи с потребностью, с одной
стороны, отыскивать функции по их
производным.
Например, находить функцию,
выражающую путь, пройденный
движущейся точкой, по скорости этой
точки.
8.
А с другой — измерять площади, объёмы,длины дуг, работу сил за определённый
промежуток времени и т. п. В
соответствии с этим различают
неопределённые и определённые
интегралы, вычисление которых является
задачей интегрального исчисления.
9.
Немецкий учёный Г. Лейбницодновременно с английским учёным
И. Ньютоном и независимо от него
открыл основные принципы
дифференциального и
интегрального исчислений в 80-х
годах XVII века.
10.
Теория приобрела силу после того,как Лейбницем и Ньютоном было
доказано, что дифференцирование и
интегрирование –
взаимно обратные
операции.
Исаак Ньютон
(1643 – 1727)
11.
12.
Работы Коши и Вейерштрассаподвели итог многовековому
развитию интегрального
исчисления.
Огюстен Луи Коши
(1789 – 1857)
Карл Теодор Вильгельм
Вейерштрасс (1815 -1897 )
13.
Работы Коши и Вейерштрассаподвели итог многовековому
развитию интегрального
исчисления.
Огюстен Луи Коши
(1789 – 1857)
Карл Теодор Вильгельм
Вейерштрасс (1815 -1897 )
14. Учебный вопрос.
Первообразная инеопределенный интеграл.
15. Первообразная и неопределённый интеграл.
Определение. Функция F(x) называетсяпервообразной для функции f(x) на отрезке
[a; b] если во всех точках этого отрезка
выполняется равенство F’(x)=f(x).
Пример. Найти первообразную от функции
f x x
2
Из определения первообразной следует, что
x3 . Действительно,
F ( x)
3
x3 1 3
1
F '( x) ' x ' 3x 2 x 2
3
3 3
16.
Замечание. Задача отыскания функции по заданнойпроизводной этой функции решается, например, в
инерциальных системах счисления пути самолёта. В
них с помощью акселерометров определяются
ускорения движения самолёта. По ускорениям
вычисляются скорости, а по скоростям – пройденный
самолётом путь с указанием его текущих координат.
Замечание. Легко видеть, что если для данной
функции f(x) существует первообразная, то эта
первообразная не является единственной.
17.
Пример.Рассмотрим функцию
f ( x) x 2 и найдём её первообразные.
Решение. Первообразные
1 3
F1 ( x) x
3
1 3
F2 ( x) x 1
3
1 3
F3 ( x) x 1
3
18.
Теорема. Если F(x)– первообразная
для функции f(x), то любая
первообразная для f(x) имеет вид
Ф(x)=F(x)+C, где C=const.
19.
Доказательство. В силу определенияпервообразной : F’(x)=f(x). Пусть Ф(x) – другая
первообразная, тогда Ф’(x)=f(x). Рассмотрим
функцию
.
Найдём
'( x) F ( x) ( x) ' F '( x) '( x)
f ( x) f ( x) 0
Таким образом, производная равная нулю. Такое
возможно лишь если
, ( x) C
Следовательно, ( x) F ( x) ( x) C
F ( x ) ( x ) C
откуда
▲
20.
Определение. Совокупность всехпервообразных F ( x) ( x) C для функции
f(x) на некотором интервале называется
неопределённым интегралом от функции
f(x) на этом интервале и обозначается
f x dx F x С
где - знак интеграла,
f x dx - подынтегральное выражение,
- подынтегральная функция.
21.
Пример. cos( x)dx sin( x) CПроверим результат:
sin x С
cos x
Отыскание всех первообразных для данной
функции или одной из них называется
интегрированием.
Интегрирование – есть действие, обратное
дифференцированию. С геометрической точки
зрения неопределённый интеграл представляет
совокупность (семейство) интегральных
кривых .
22.
Естественно возникает вопрос: для всякой лифункции f ( x )существуют первообразные, а значит
и неопределённый интеграл?
На этот вопрос отвечает теорема
существования неопределённого интеграла, которую
мы примем без доказательства.
Теорема. Если функция f ( x ) непрерывна на
некотором интервале, то для неё на этом
интервале существует первообразная, то
есть неопределённый интеграл.
23. УЧЕБНЫЙ ВОПРОС,
Основные свойстванеопределённого интеграла.
24. Основные свойства неопределённого интеграла.
1. Производная от неопределённогоинтеграла равна подынтегральной
функции: если F x f x ,
то
f x dx F x С f x
2. Дифференциал от неопределённого
интеграла равен подынтегральному
выражению, то есть
d
f x dx f x dx
25.
3. Неопределённый интеграл отдифференциала некоторой функции равен
этой функции, плюс произвольная
постоянная
d F x F x С
Справедливость последующего равенства
легко проверить дифференцированием
(дифференциалы от обеих частей равенства
равны
d F x
26.
4. Неопределённый интеграл оталгебраической суммы функций равен
алгебраической сумме интегралов от
слагаемых
(
f
(
x
)
g
(
x
))
dx
f ( x)dx g ( x)dx
27.
5. Числовой множитель можно выноситьза знак неопределенного интеграла:
C
f
(
x
)
dx
C
f
(
x
)
dx
.
28.
6. Свойство инвариантности (постоянства) формулинтегрирования.
Всякая формула интегрирования сохраняет
свой вид при подстановке вместо
независимой переменной любой
дифференцируемой функции,
т.е., если
f x dx F x С ,
то
f u du F u С
29.
Доказательство.Возьмём функцию
F u F x ;
для её дифференциала в силу теоремы об
инвариантности вида первого
дифференциала имеем:
d F u F u du f u du
отсюда
f u du
d F u F u С
▲
30. 7.
1f (kx b)dx F (kx b) C
k
31.
а. F(x) =Сх+С11.f(x) = хn
б. F(x) =
2.f(x) = C
в. F(x) =tg x+С
3.f(x)=sinx
1
4.f(x) = cos 2 x
г. F(x) = sin x+С
д. F(x) = сtg x+С
5.f(x) =cosx
6.f(x)=
x n 1
С
n 1
1
2
sin x
е. F(x) = - cos x+С
32. Таблица основных интегралов (через u(x)!)
1. u dxu
1
C , где 1
1
du
2.
u ln u C
3.
sin u dx cos u C
4.
cos u dx sin u C
5.
dx
cos2 u tg u C
33.
6.dx
sin 2 u ctgu C
7.
tgudu
ln
cos
u
C
8.
ctgudu
ln
sin
u
C
9.
e
du
e
C
u
u
u
a
10. a du
C
ln a
u
34.
du1
u
11.
arctg
C
2
2
a u a
a
du
1
a u
a2 u 2 2a ln a u C
dx
u
13.
a 2 u 2 arcsin a C
12.
14.
dx
u a
2
ln u u a C
2
2
2
35.
15.16.
du
u
ln
tg
C
sin u
2
du
u
cos u ln tg 2 4 C
36.
Замечание. Таблица основных интеграловв силу свойства инвариантности формул
интегрирования оказывается
справедливой независимо от того,
является ли переменная интегрирования
независимой переменной или любой
дифференцируемой функцией от неё.
37.
Пример.5
1
sin(5 x)dx sin(5 x) 5 dx sin(5 x) 5 d 5 x
5x t
1
1
sin(5 x)d 5 x
sin tdt
d (5 x) dt 5
5
1
1
cos t C cos 5 x C
5
5
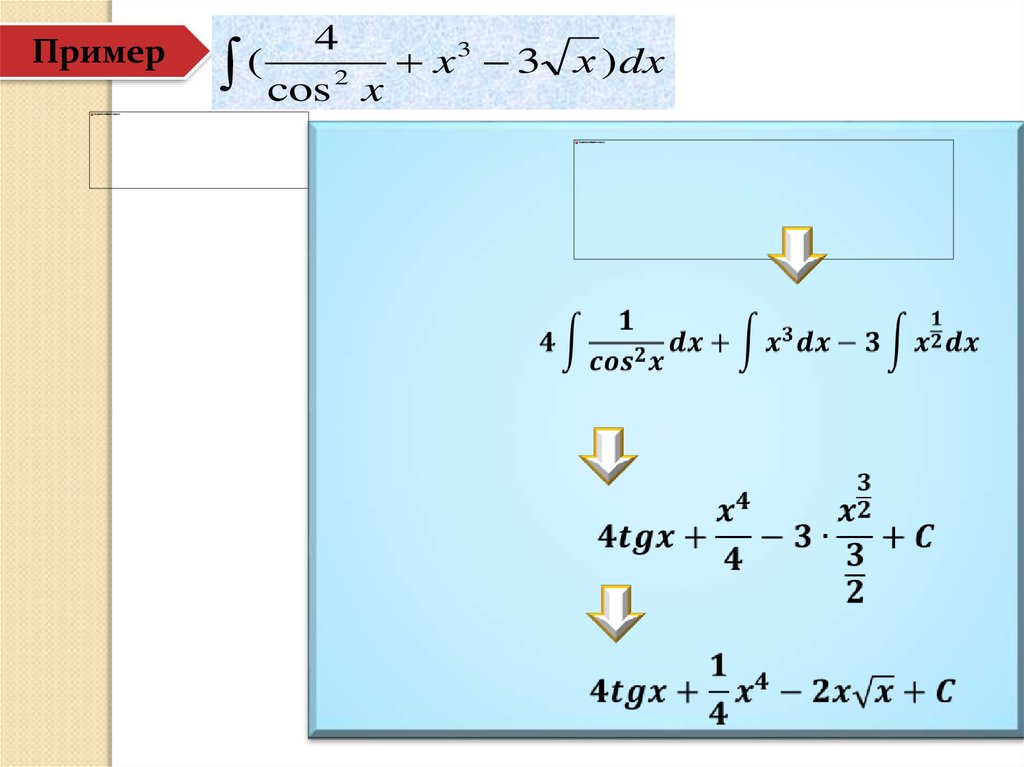
38.
Пример4
3
(
x
3 х ) dx
cos 2 x
39. Найти интегралы для функций:
1) f(x) =10х2) f(x) =3 х²
3) f(x) = sinх+5
4) f(x) = 5cosx
5) f(x) = 6х²
6) f(x) = 3-2х
40. Верно ли что:
а)в)
x
dx
5
x
C
5
4
3
x
dx
x
C
2
г)
б)
3
x
dx
6
x
C
2
3
41. УЧЕБНЫЙ ВОПРОС
Интегрированиеразложением, внесением
под знак дифференциала.
42.
Непосредственное интегрирование вычисление интеграла с помощью• его свойств,
• тождественных преобразований
подынтегральной функции,
• таблицы основных интегралов.
Использование при этом свойства
линейности неопределённого интеграла
называется методом разложения
вычисления интеграла.
43.
Таблица основных интегралов в силу.
свойства инвариантности формул
интегрирования оказывается
справедливой независимо от того,
является ли переменная
интегрирования независимой
переменной или дифференцируемой
функцией.
Например,
dx
1 5dx
1 d 5x
1
sin 2 5x 5 sin 2 5x 5 sin 2 5x 5 ctg5x C
44.
Найти интеграл2 x xe 4
dx
.
x
3
x
Решение:
2 x xe 4
2 x 4
dx
2
x
e
dx
x
x
3
x
dx 2 3 x
2 x dx e dx 4 x e 4ln x C.
x 3
2
x
45.
Интегрирование внесениемпод знак дифференциала.
Известно, что дифференциал функции
равен произведению производной этой
функции и дифференциала её аргумента:
x dx d x
Переход в этом равенстве слева
направо называют подведением
множителя x под знак
дифференциала.
46. Таблица дифференциалов
47.
Пусть требуется найти интеграл видаf x x dx.
Подводя в этом интеграле множитель
x под знак дифференциала, а затем
используя свойство инвариантности
формул интегрирования, получим
x dx f x d x F x C ,
f
x
если
f
x
dx
F
x
C
.
48.
Метод интегрирования введением подзнак дифференциала используется для
интегрирования сложных функций:
• аргумент сложной функции записывается
под знак дифференциала;
• затем необходимо разделить
подынтегральное выражение на
производную этого аргумента.
49.
Пример. Найти интегралdx
2 x 3
5
2 x 3 dx
5
dx
2 x 3
5
2 x 3
.
d 2 x 3
2
5
1
5
2 x 3 d 2 x 3 .
2
Здесь подынтегральное выражение
разделено на 2, так как d 2x 3 2dx,
d 2 x 3
dx
.
2
50.
Теперь используем свойствоинвариантности и применим формулу 1
таблицы относительно переменной
интегрирования 2х – 3.
dx
1 2 x 3
1
2 x 3 5 2 4 C C 8 2 x 3 4 .
4
Таким образом,
1
f
аx
b
dx
F
(
ax
b
)
C
,
где
F
(
x
)
f
(
x
a
51.
Примеры.52.
1. F(x) =Сх+С11.f(x) = хn
2. F(x) =
2.f(x) = C
x n 1
С
n 1
3. F(x) = tg x+С
3.f(x)=sinx
1
4. F(x) = sin x+С
5.f(x) =cosx
5. F(x) = сtg x+С
4.f(x) = cos 2 x
6.f(x)=
1
2
sin x
6. F(x) = - cos x+С
53. УЧЕБНЫЙ ВОПРОС
Метод замены переменной внеопределенном интеграле.
Интегрирование функций,
содержащих квадратный трехчлен.
54.
Замена переменной или подстановка.Метод заключается во введении новой
переменной интегрирования.
При этом интеграл приводится к
новому интегралу, который является
табличным или к нему сводящимся (в
случае «удачной» подстановки).
Общих методов подбора подстановок
не существует.
55.
Введём в интеграле f x dx новуюпеременную t, положив x=φ(t), где φ(t) –
непрерывная, дифференцируемая
функция. Тогда dx=φ’(t) dt и справедливо
равенство
f x dx f t t dt
Это формула замены переменной
или метода подстановки. После этого
получим новый интеграл, который
проще приводится к табличному.
56.
Доказательство.Находим производную от левой части
равенства
.
f x dx
x
f x
Правую часть равенства будем
дифференцировать по x как сложную
функцию, где t – промежуточный аргумент,
при этом dx
и по правилу
dt
t
дифференцирования обратной функции
dt
1
dx t
57.
Таким образом, имеемdt
f
t
t
dt
f
t
t
dt
x
t dx
.
1
f t t
f t f x
t
Следовательно, производные по х от
правой и левой частей равенства равны,
что и требовалось доказать. ▲
58.
Замечание 1. После интегрированияв правой части равенства вместо t
необходимо подставить его выражение
через x на основании равенства x=φ(t).
Замечание 2. При замене
переменной функцию x=φ(t) надо
подбирать так, чтобы новый интеграл
стал проще.
Замечание 3. При интегрировании
иногда целесообразно подбирать
замену переменной не в виде x=φ(t), а в
виде t=ψ(x).
59.
60.
61. Интегрирование функций, содержащих квадратный трехчлен.
62.
63.
64. Задание на самостоятельную работу
[1] Н.С. Пискунов. Дифференциальное иинтегральное исчисления. Т 1. Москва: ИнтегралПресс, 2004, с. 340-375.
[3] Б.П. Демидович, В.А. Кудрявцев. Краткий
курс высшей математики. Москва: Издательство
АСТ, 2004, с. 229-250.
Выучить таблицу основных интегралов.
65. Математика ППИ
Лекция 12.Метод интегрирования по частям в
неопределенном интеграле. Интегрирование
тригонометрических функций
66. Вопросы лекции
1. Интегрирование по частям внеопределенном интеграле.
2. Интегрирование
тригонометрических функций.
67.
УЧЕБНЫЙ ВОПРОСИнтегрирование по частям.
68.
Одной из причин сложности операцииинтегрирования является отсутствие
формулы интегрирования произведения
функций.
Есть метод интегрирования
произведения некоторых классов
функций, который называется методом
интегрирования по частям.
Выведем формулу интегрирования по
частям.
69.
Пусть u=u(x) и v=v(x) –дифференцируемые функции и
d u v udv vdu
Отсюда, интегрируя последнее
равенство, получаем:
u v udv vdu
или
udv
u
vdu
формулой интегрирования по частям.
70.
Успех формулы интегрирования почастям зависит от умения правильно разбить
подынтегральное выражение на множители u
и dv.
Как правило, за u выбирается функция,
которая при дифференцировании
упрощается.
Иногда необходимо применять
интегрирование по частям последовательно
несколько раз.
Укажем некоторые часто встречающиеся
интегралы, которые вычисляются методом
интегрирования по частям.
71.
I. Интегралы вида:P x ln xdx, P x log xdx, P x arcsin x dx, P x arccos xdx,
P x arctg xdx, P x arcctg xdx,
a
где P(x) – многочлен.
Во всех случаях за u при
интегрировании по частям применяют
функцию, являющуюся множителем
после P(x).
72.
kxP
x
e
dx,
kx
P
x
a
dx,
P x sin kx dx, P x cos kxdx,
73.
Решение.(опечатка
в du)
v
74.
75. Контрольные вопросы:
1. В чем заключается метод непосредственногоинтегрирования ?
2. В чем заключается метод интегрирования
заменой?
3. В чем заключается метод интегрирования по
частям?





























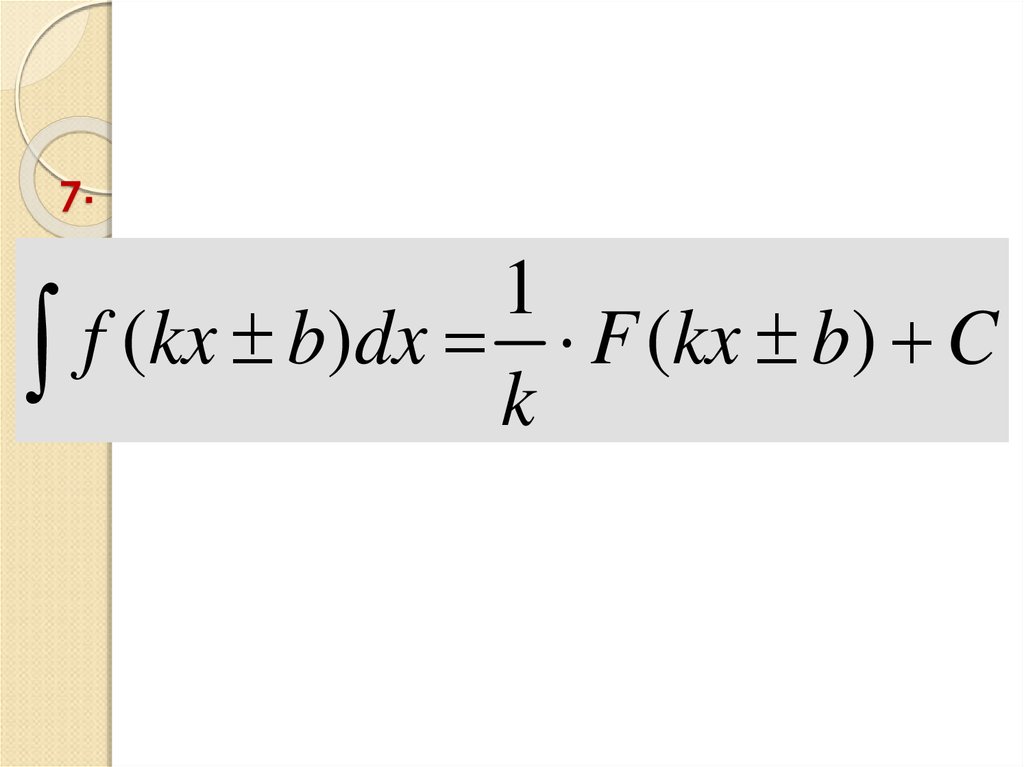


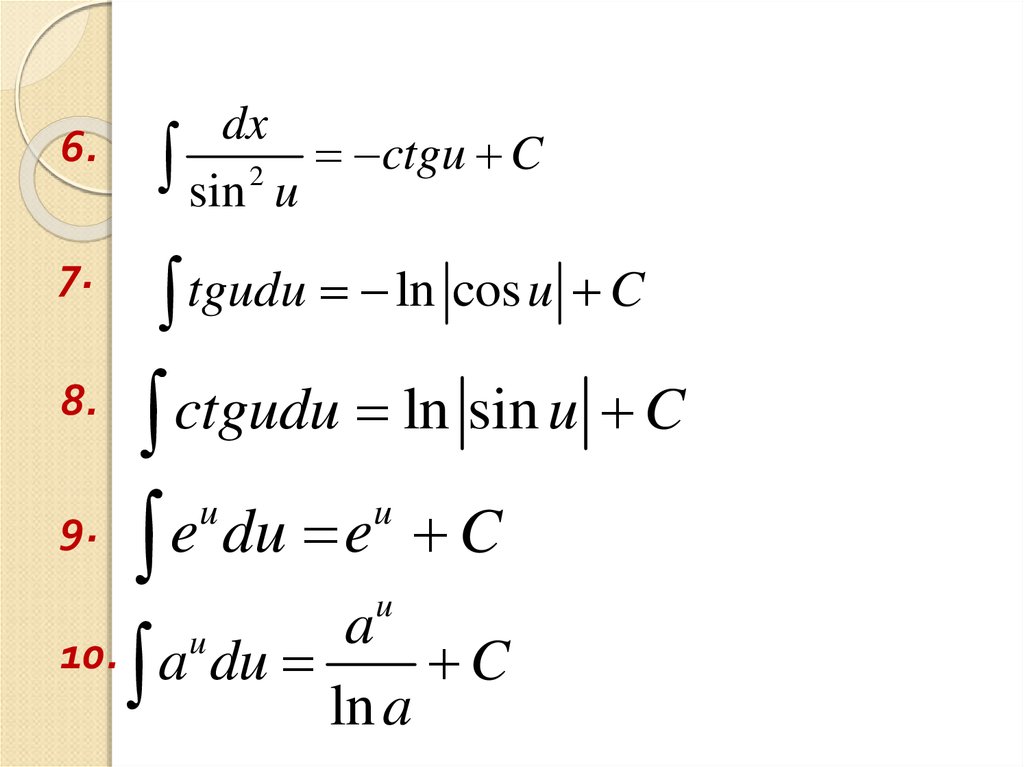
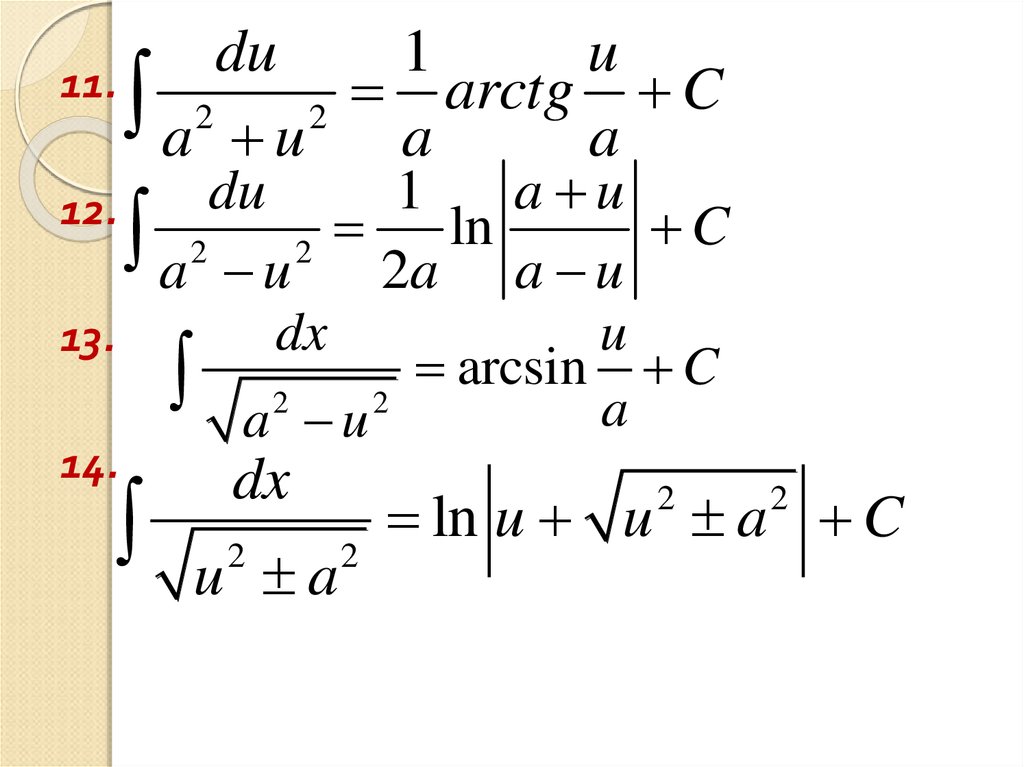
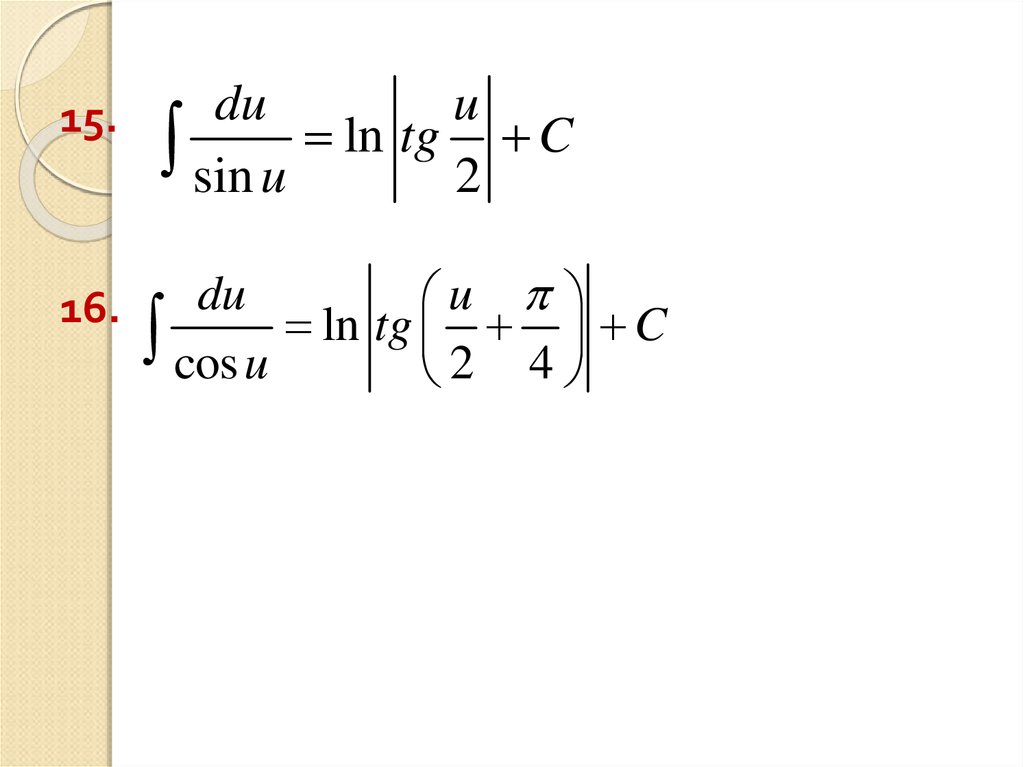

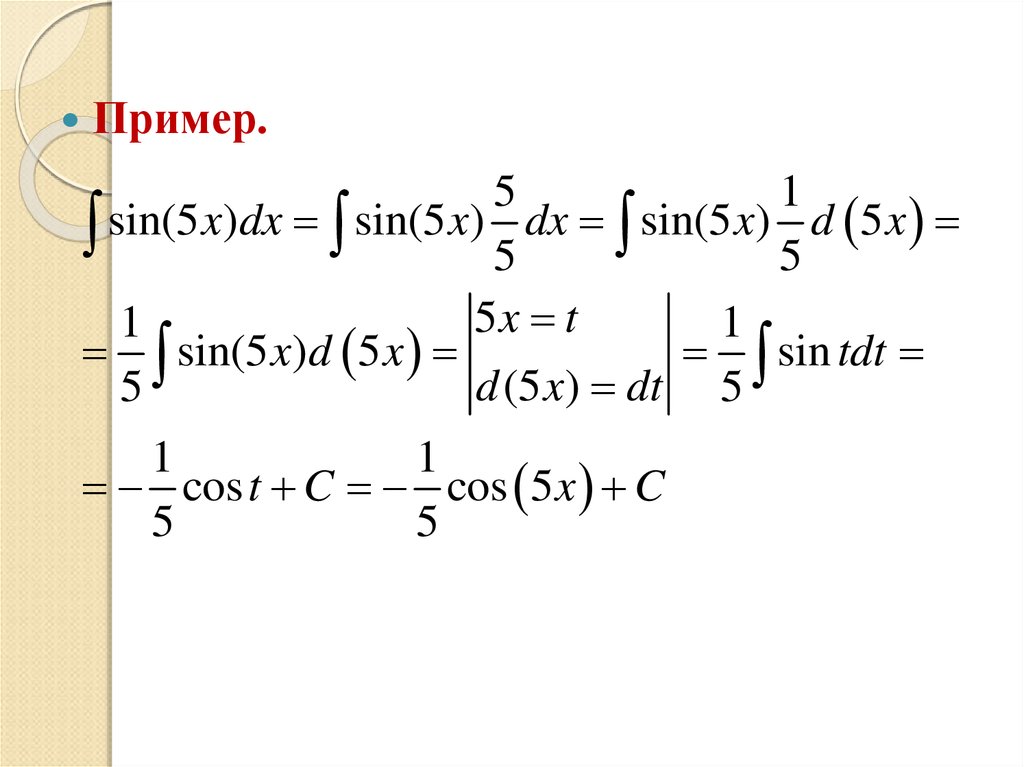




















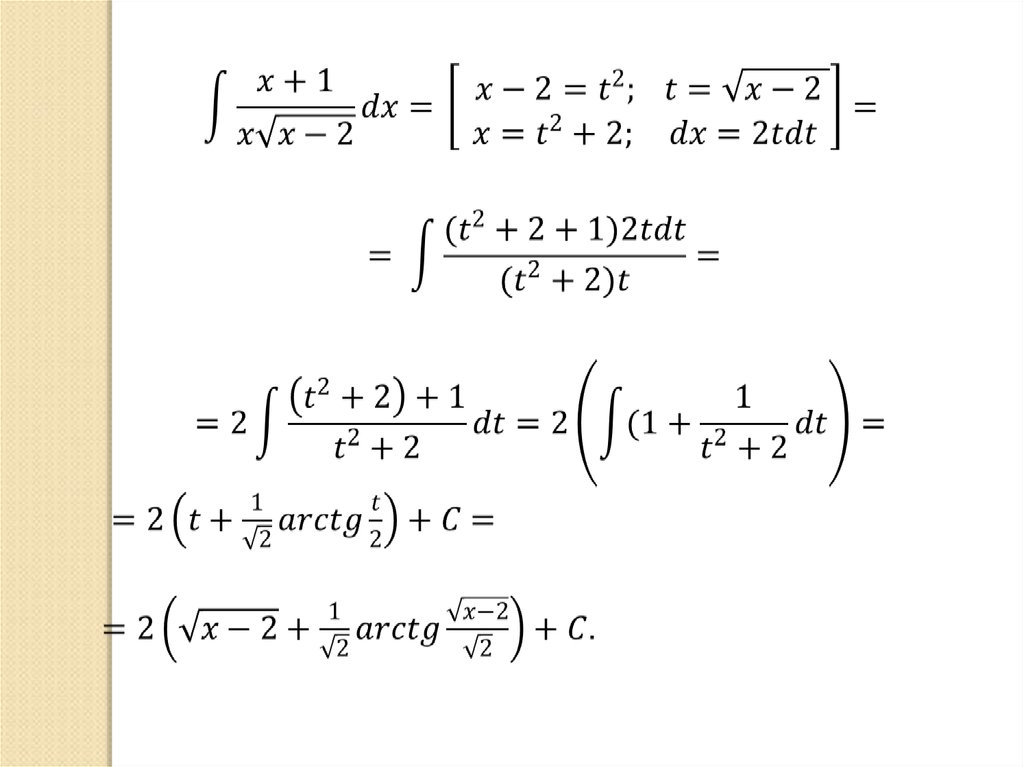
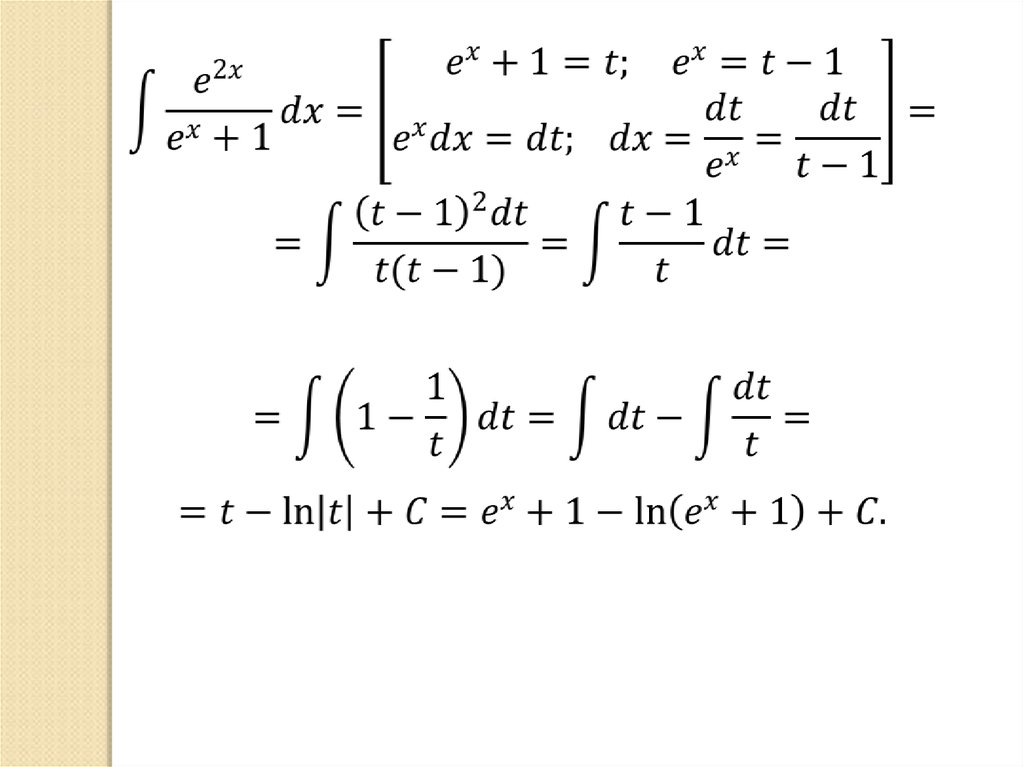














 Математика
Математика








