Пирамиды. Примеры пирамид. Определения

1.

2.

Стоит на земле пирамида, и Боги о ней говорят.
На ней не рванье, не хламида, а вечного камня наряд.
Она здесь стоять не устала, хоть минуло много веков,
Она головою достала до самых, седых облаков.
Что людям она сохранила?
Великих камней забытье?
Зрачки желтого Нила лениво глядят на нее.
Кто спит в этой древней мгле?
Расскажут ли камни о том,
Как всех их слезами солили и кровью кропили потом.
Стоит на земле пирамида, и Боги о ней говорят.
На ней не рваны, не хламида, а вечного камня наряд

3. Пирамиды древности

4. Пирамиды древности

5. Пирамиды древности

6.

Париж.
Новый вход в Лувр
Париж.
Новый проект.
Севастополь. Храм-пирамида.

7. Магические пирамиды

8. Пирамиды

9. Примеры пирамид

10. Определения

• Евклид, пирамиду определяет как
телесную фигуру, ограниченную
плоскостями, которые от
каждойплоскости сходятся к одной точке.
• Герон предложил следующее
определение пирамиды: “Это фигура,
ограниченная треугольниками,
сходящимися в одной точке и основанием
которой служит многоугольник”.

11.

S – вершина пирамиды
ABCDE – основание пирамиды
S
Вершина
пирамиды
Основание
пирамиды
B
A
C
E
D

12.

Отрезки, соединяющие вершину пирамиды с
вершинами основания, называются
боковыми рёбрами
SA, SB, SC, SD, SE - боковые рёбра пирамиды
S
SABCDЕ.
Боковые
рёбра
пирамиды
B
A
C
E
D

13.

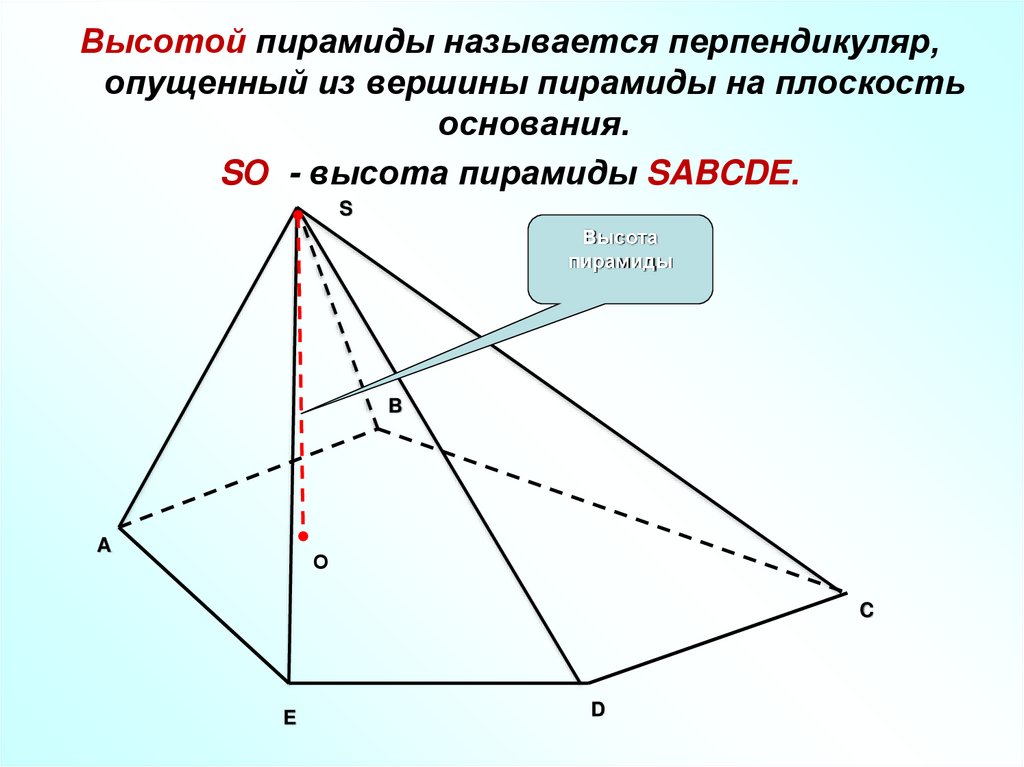
Высотой пирамиды называется перпендикуляр,
опущенный из вершины пирамиды на плоскость
основания.
SО - высота пирамиды SABCDЕ.
S
Высота
пирамиды
B
A
О
C
E
D

14.

F
S
C
P
K
O
M
B
A
N
O
M
C
P
R
K
S
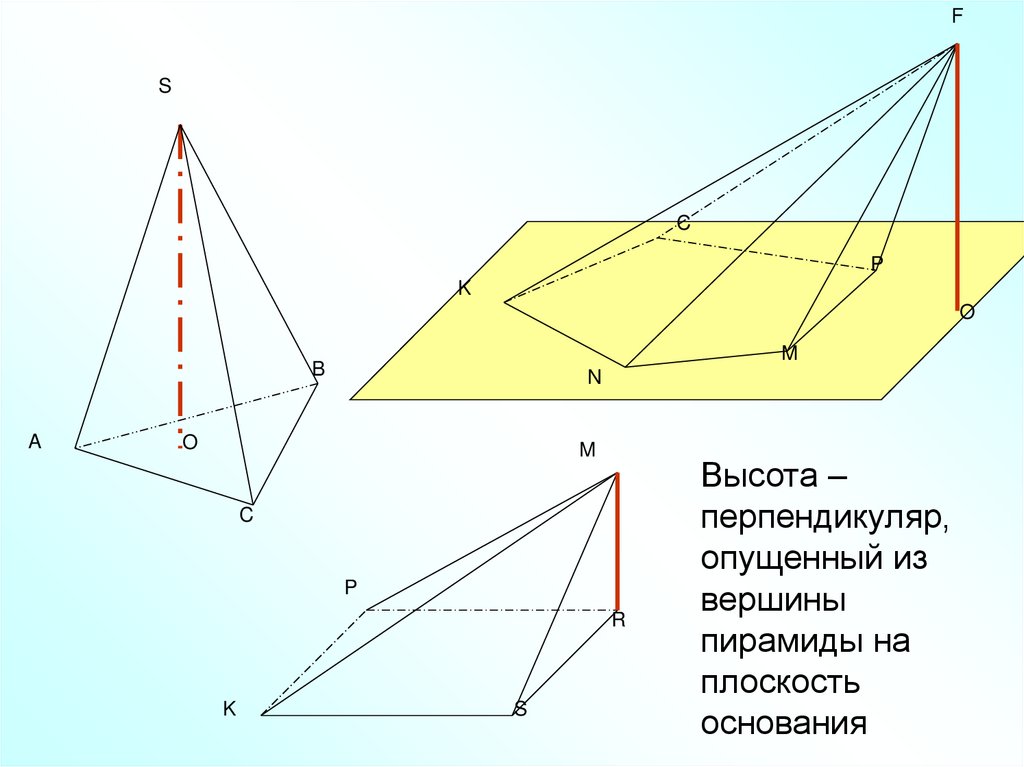
Высота –
перпендикуляр,
опущенный из
вершины
пирамиды на
плоскость
основания

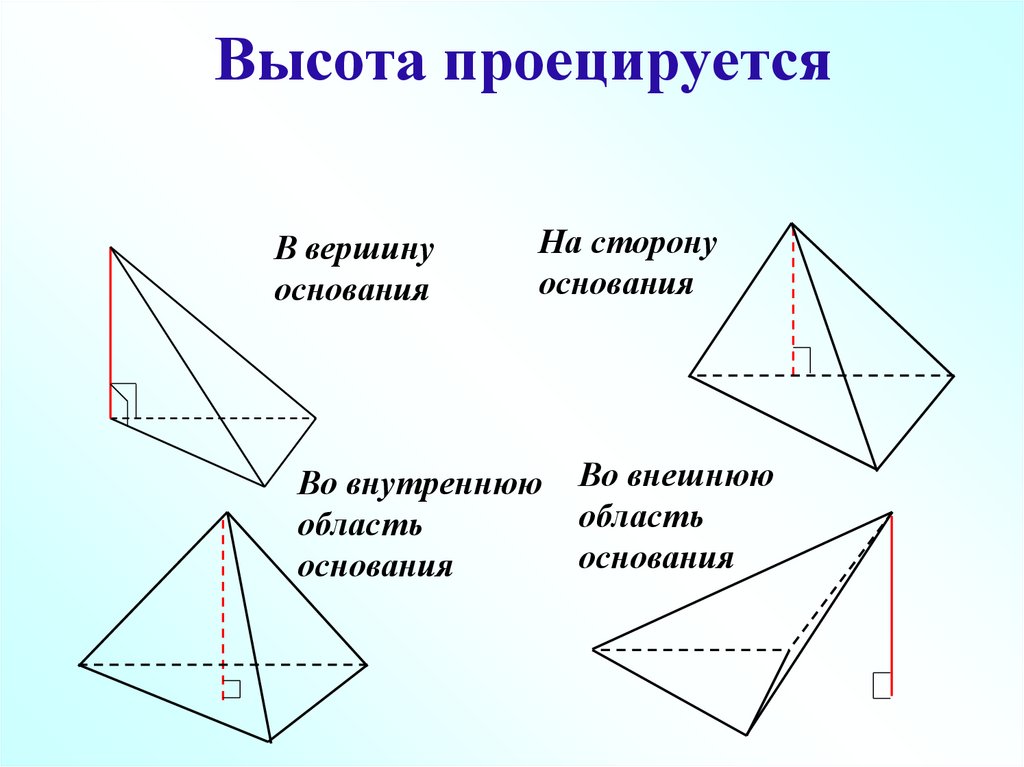
15. Высота проецируется

В вершину
основания
На сторону
основания
Во внутреннюю
область
основания
Во внешнюю
область
основания

16.

S
S
D
C
Н
А
B
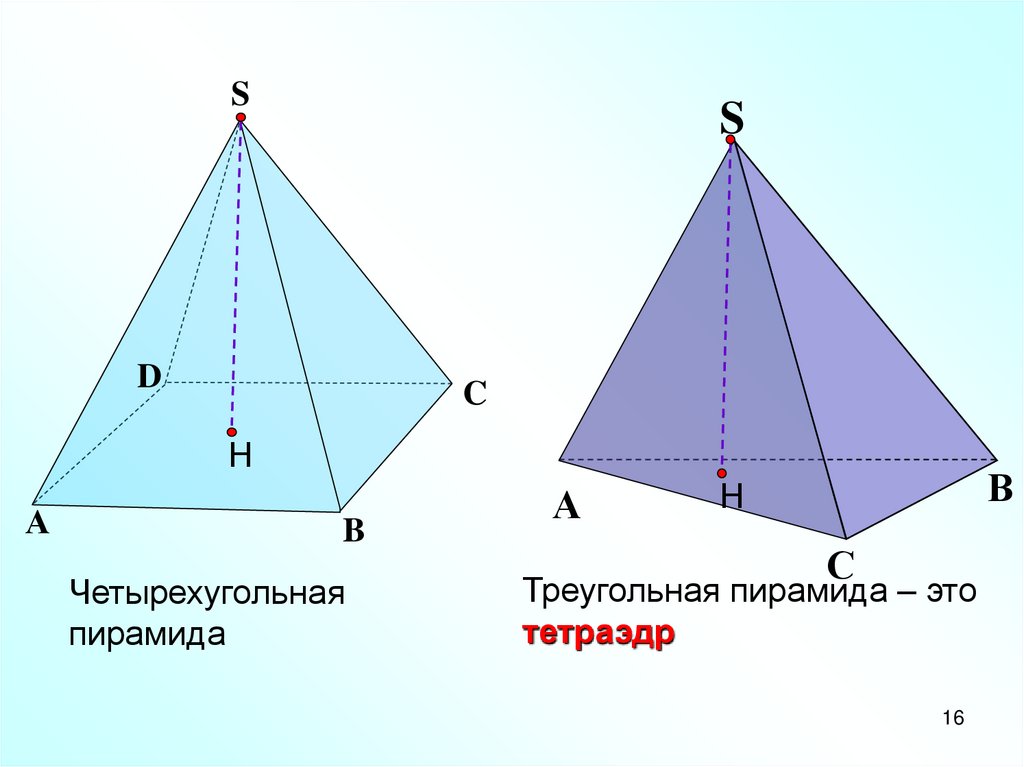
Четырехугольная
пирамида
А
В
Н
С
Треугольная пирамида – это
тетраэдр
16

17.

Пятиугольная
пирамида
Р
Шестиугольная
пирамида
Аn
Н
А1
А3
А2
Н
17

18.

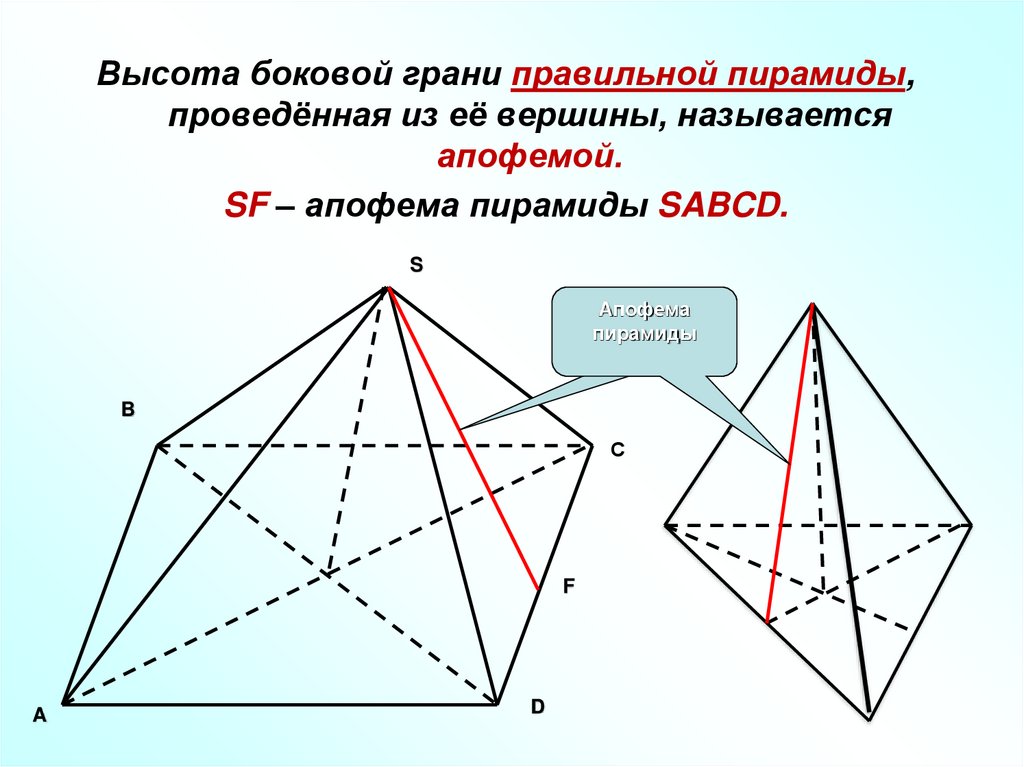
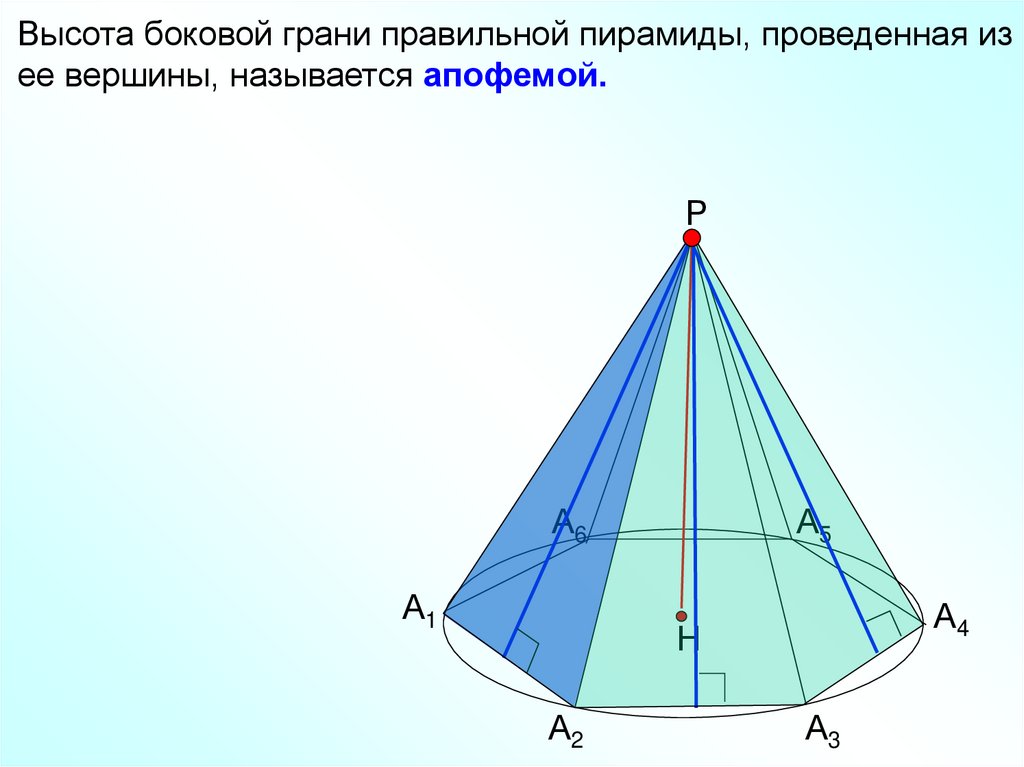
Высота боковой грани правильной пирамиды,
проведённая из её вершины, называется
апофемой.
SF – апофема пирамиды SABCD.
S
Апофема
пирамиды
B
С
F
A
D

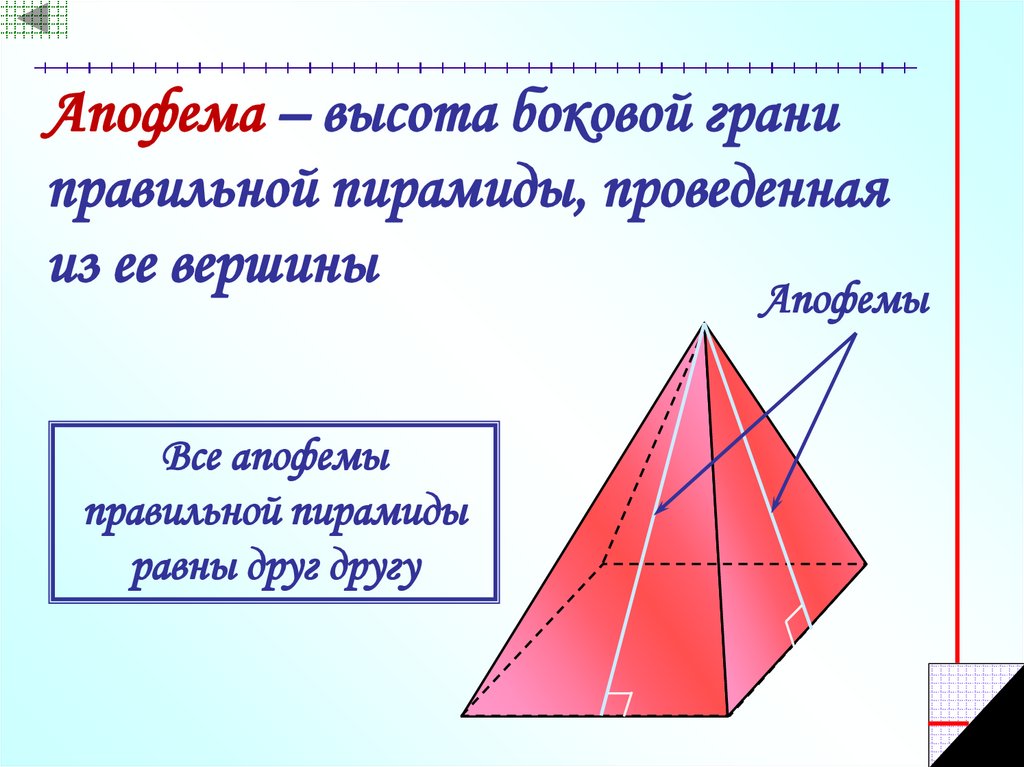
19. Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины

Апофемы
Все апофемы
правильной пирамиды
равны друг другу

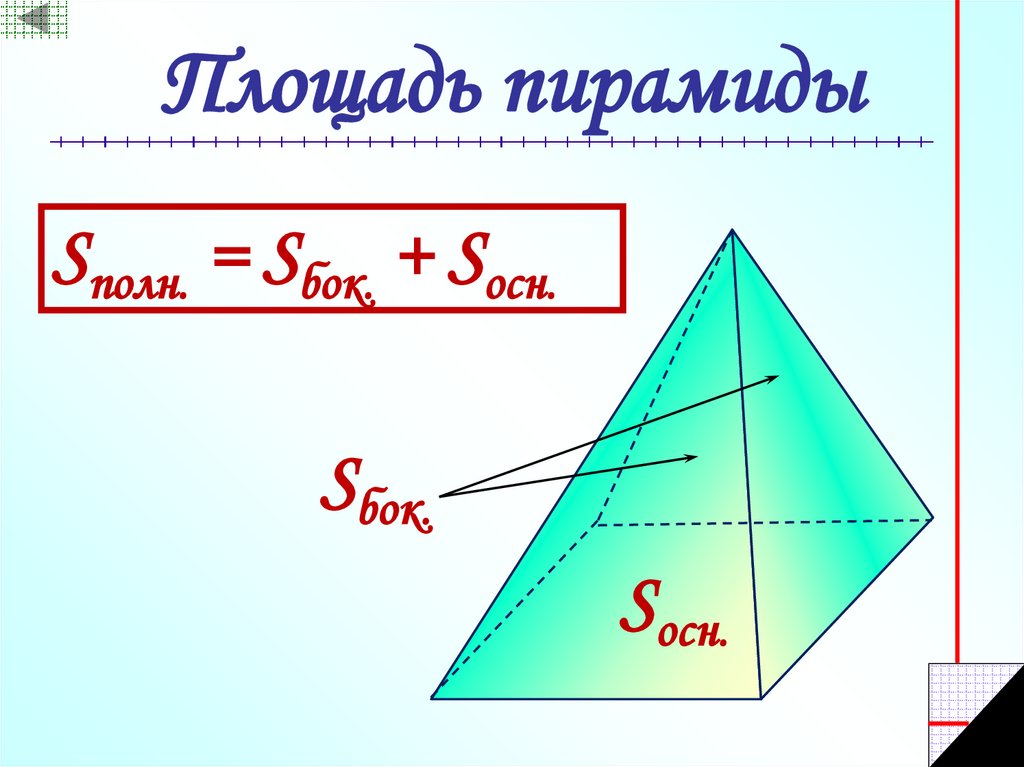
20. Площадь пирамиды

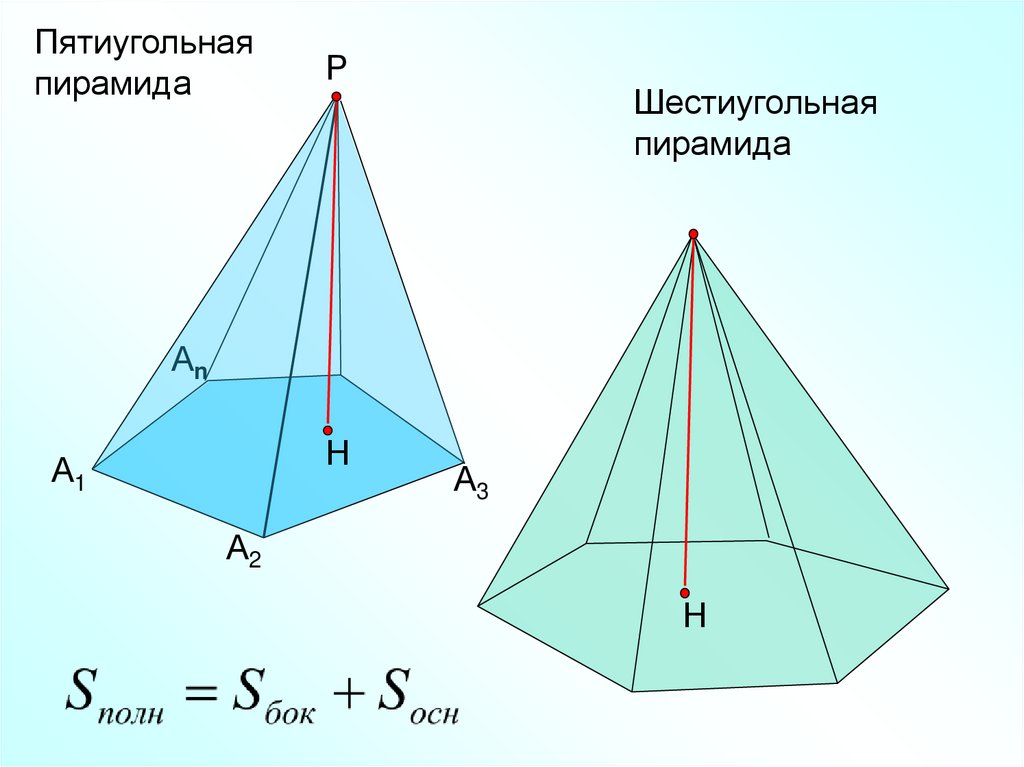
Sполн. = Sбок. + Sосн.
Sбок.
Sосн.

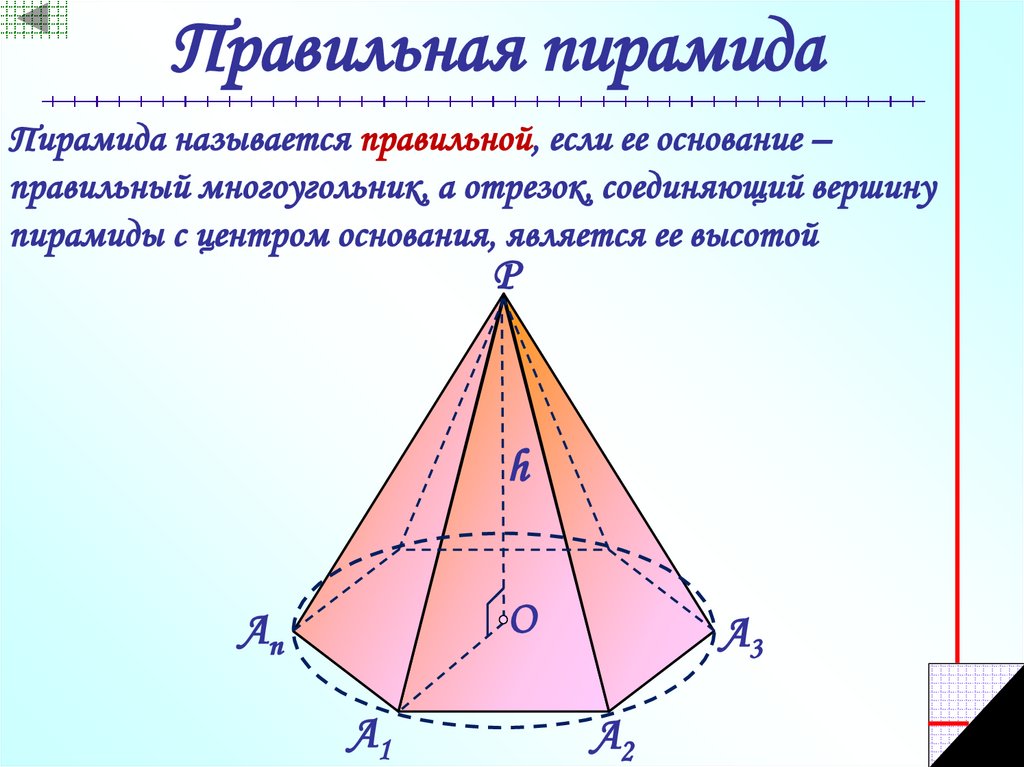
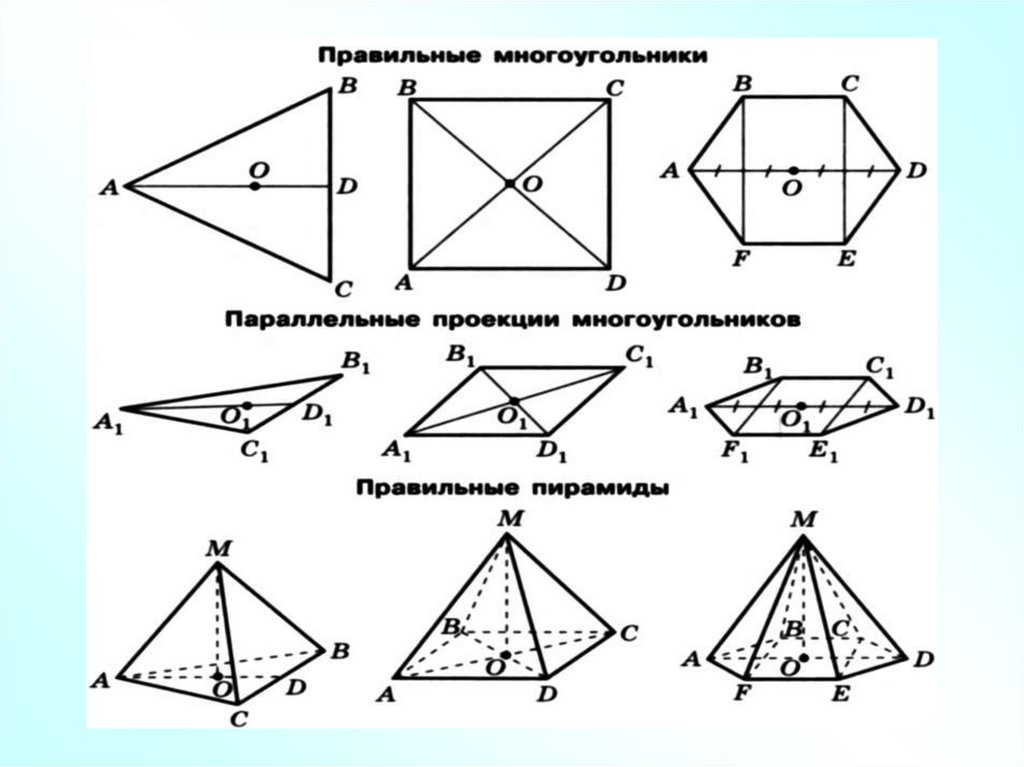
21. Правильная пирамида

Пирамида называется правильной, если ее основание –
правильный многоугольник, а отрезок, соединяющий вершину
пирамиды с центром основания, является ее высотой
P
h
O
Аn
А1
А3
А2

22.

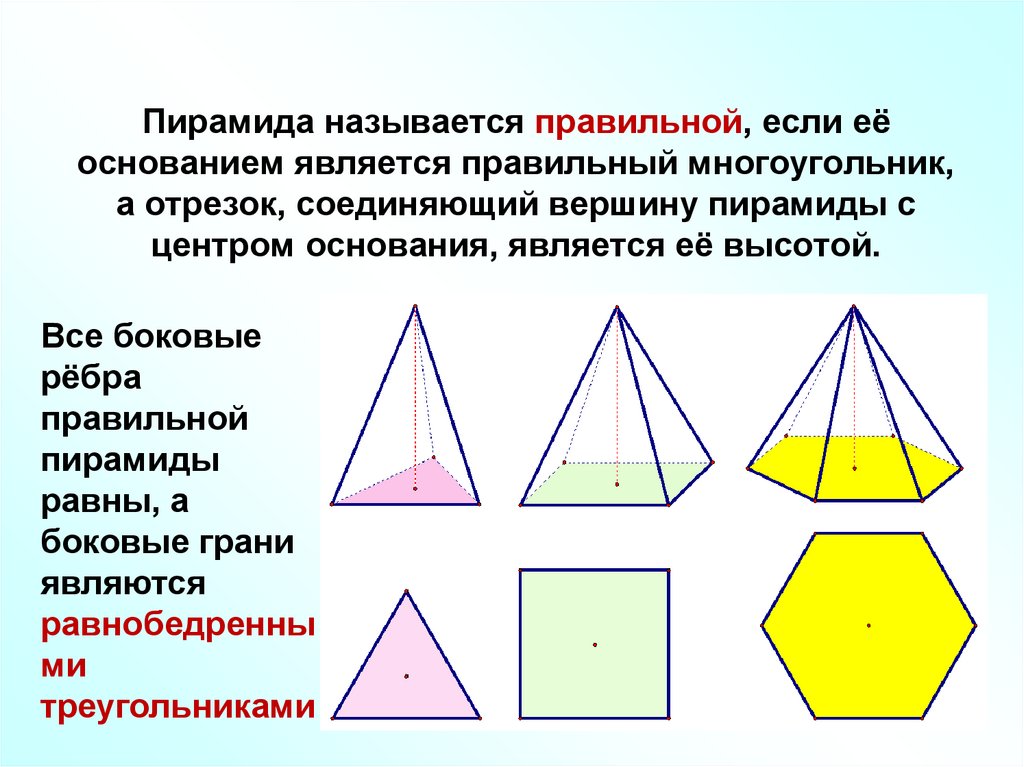
Пирамида называется правильной, если её
основанием является правильный многоугольник,
а отрезок, соединяющий вершину пирамиды с
центром основания, является её высотой.
Все боковые
рёбра
правильной
пирамиды
равны, а
боковые грани
являются
равнобедренны
ми
треугольниками

23.

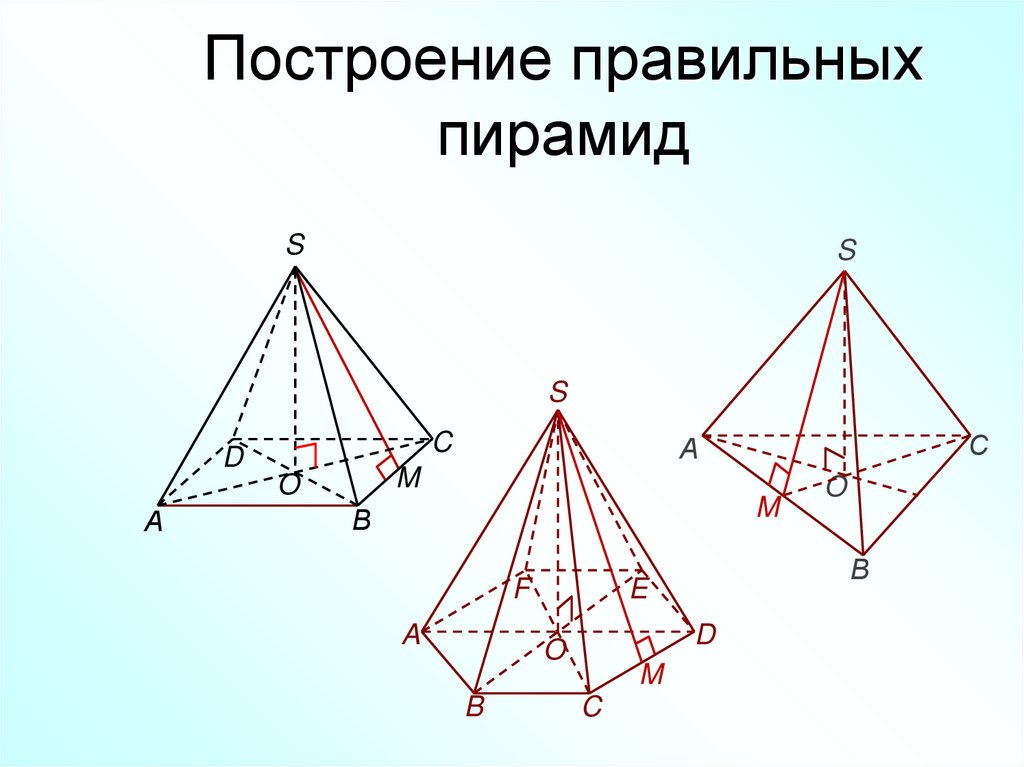
24. Построение правильных пирамид

S
S
S
C
D
M
O
А
С
А
M
В
F
A
B
В
E
D
O
M
C
O

25.

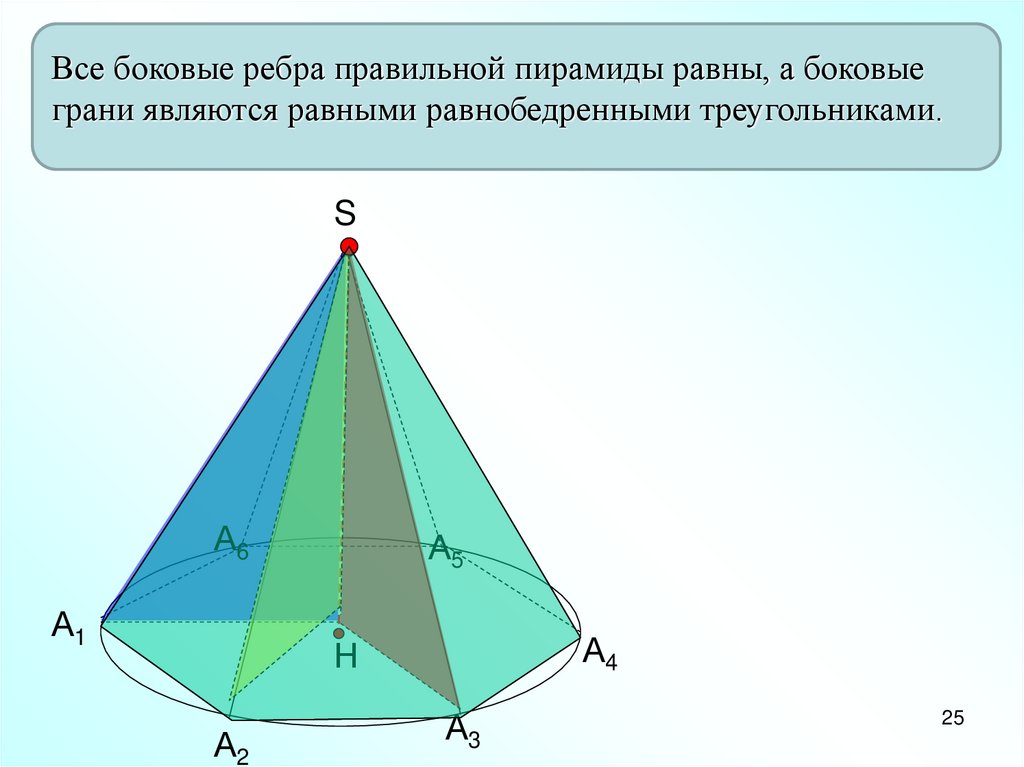
Все боковые ребра правильной пирамиды равны, а боковые
грани являются равными равнобедренными треугольниками.
S
А6
А1
А5
А4
Н
А2
А3
25

26.

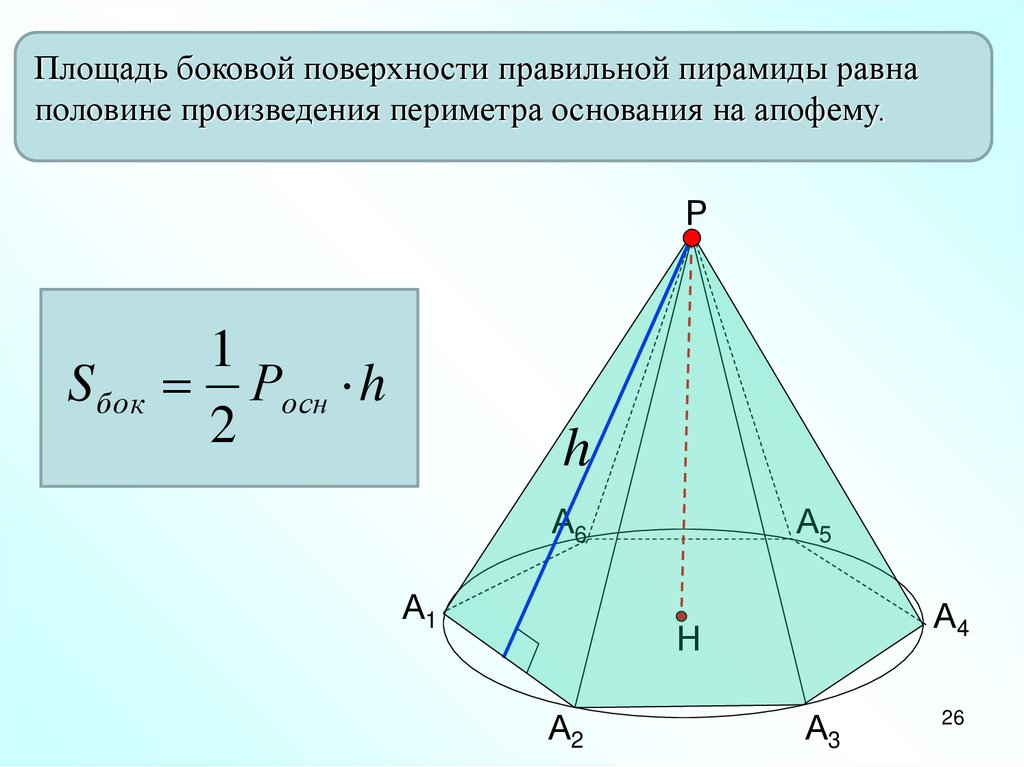
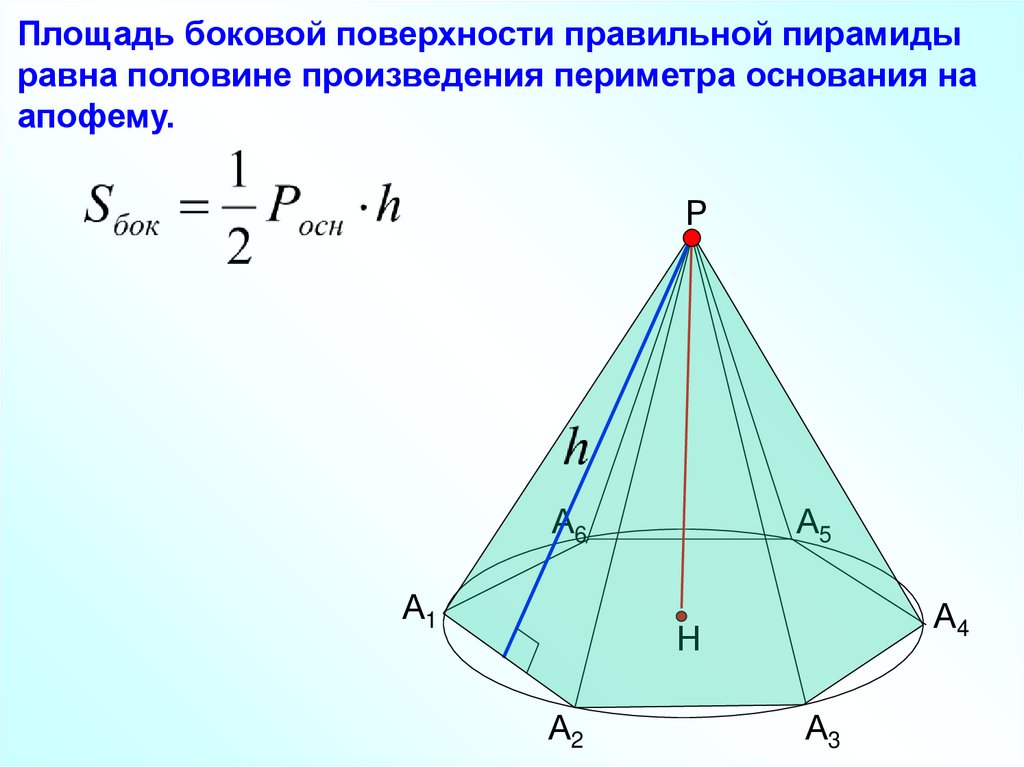
Площадь боковой поверхности правильной пирамиды равна
половине произведения периметра основания на апофему.
Р
1
S бок Росн h
2
h
А6
А1
А5
А4
Н
А2
А3
26

27.

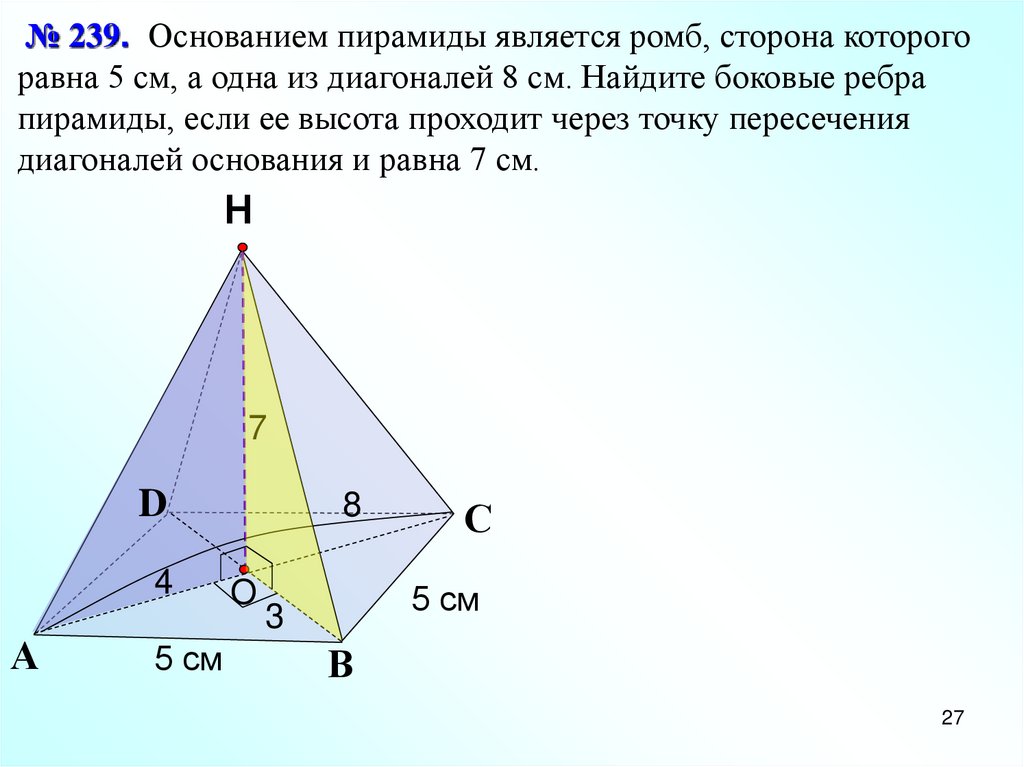
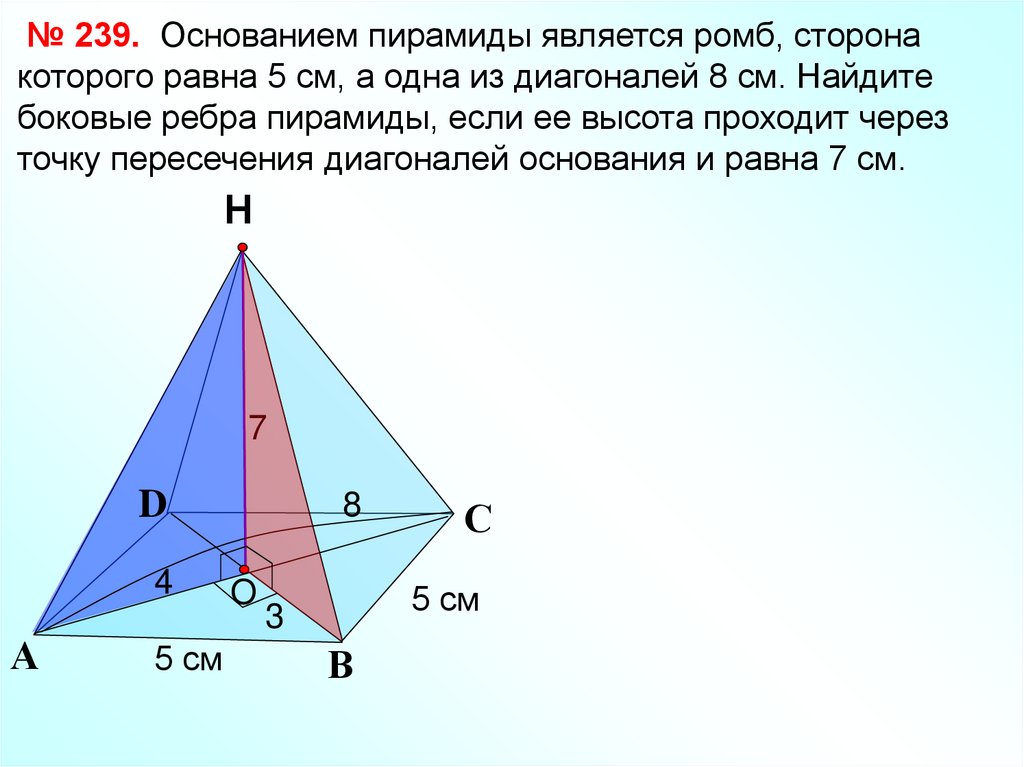
№ 239. Основанием пирамиды является ромб, сторона которого
равна 5 см, а одна из диагоналей 8 см. Найдите боковые ребра
пирамиды, если ее высота проходит через точку пересечения
диагоналей основания и равна 7 см.
Н
7
D
4
А
5 см
8
O
С
5 см
3
В
27

28.

№ 243. Основанием пирамиды DАВС является треугольник АВС, у
которого АВ = АС = 13 см, ВС = 10 см; ребро АD перпендикулярно
к плоскости основания и равно 9 см. Найдите площадь боковой
поверхности пирамиды.
D
9
13
В
10
M
А
13
С
28

29.

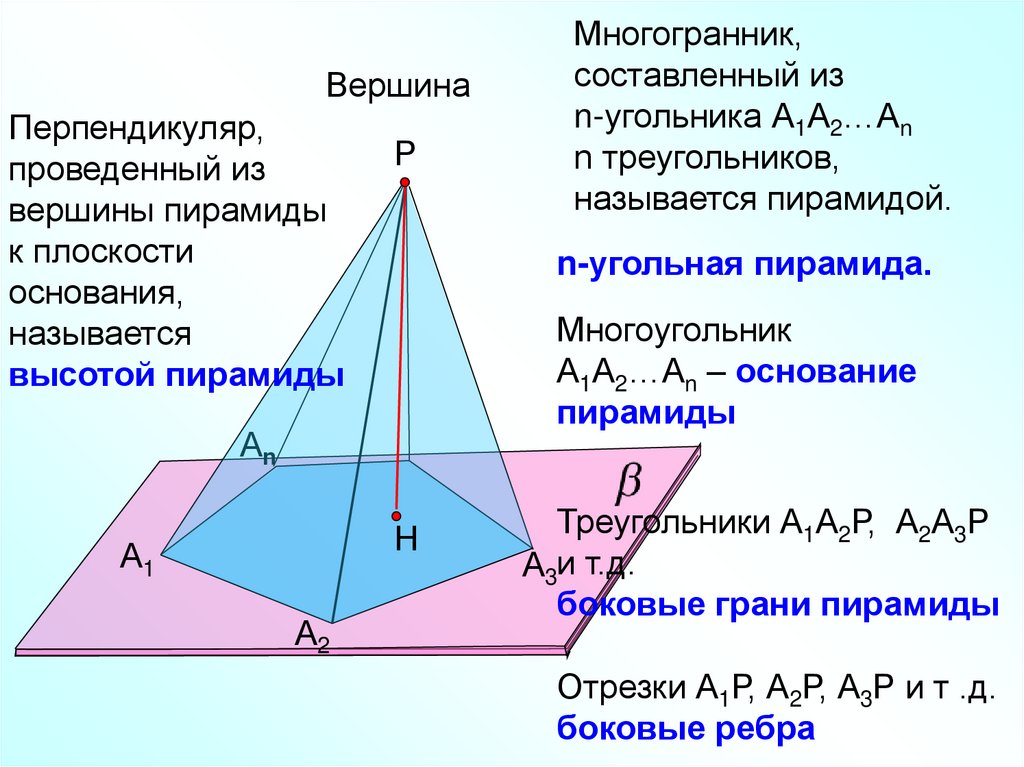
Вершина
Перпендикуляр,
проведенный из
вершины пирамиды
к плоскости
основания,
называется
высотой пирамиды
Р
n-угольная пирамида.
Многоугольник
А1А2…Аn – основание
пирамиды
Аn
Н
А1
А2
Многогранник,
составленный из
n-угольника А1А2…Аn
n треугольников,
называется пирамидой.
Треугольники А1А2Р, А2А3Р
А3и т.д.
боковые грани пирамиды
Отрезки А1Р, А2Р, А3Р и т .д.
боковые ребра

30.

Пятиугольная
пирамида
Р
Шестиугольная
пирамида
Аn
Н
А1
А3
А2
Н

31.

Пирамида называется правильной, если ее основаниеправильный многоугольник, а отрезок, соединяющий вершину
с центром основания, является ее высотой.
Центром правильного
многоугольника называется центр
вписанной (или описанной около
него окружности).
Н

32.

Докажем, что все боковые ребра правильной пирамиды
равны, а боковые грани являются равными
равнобедренными треугольниками.
Р
А6
А1
А5
А4
Н
А2
А3

33.

Высота боковой грани правильной пирамиды, проведенная из
ее вершины, называется апофемой.
Р
А6
А1
А5
А4
Н
А2
А3

34.

Площадь боковой поверхности правильной пирамиды
равна половине произведения периметра основания на
апофему.
Р
А6
А1
А5
А4
Н
А2
А3

35.

№ 239. Основанием пирамиды является ромб, сторона
которого равна 5 см, а одна из диагоналей 8 см. Найдите
боковые ребра пирамиды, если ее высота проходит через
точку пересечения диагоналей основания и равна 7 см.
Н
7
D
4
А
5 см
8
O
С
5 см
3
В