Похожие презентации:
Корреляция и свертка
1.
Корреляция и свертка:функция корреляции,
коэффициент корреляции,
циклическая корреляция,
линейная корреляция,
быстрая корреляция,
импульсная характеристика системы,
теорема о свертке,
обращение свертки...
2.
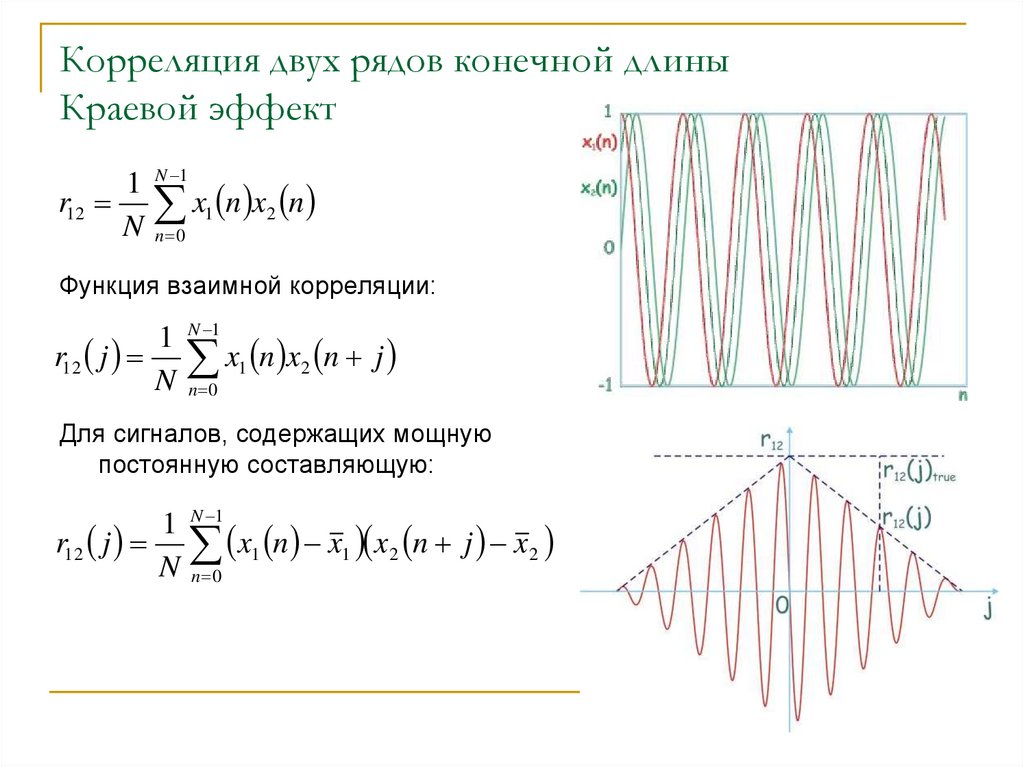
Корреляция двух рядов конечной длиныКраевой эффект
1 N 1
r12 x1 n x2 n
N n 0
Функция взаимной корреляции:
1 N 1
r12 j x1 n x2 n j
N n 0
Для сигналов, содержащих мощную
постоянную составляющую:
1 N 1
r12 j x1 n x1 x 2 n j x 2
N n 0
3.
Нормированная функция корреляцииКоэффициенты корреляции
коэффициент взаимной корреляции
N 1
12 j
x n x n j
n 0
1
2
N 1
N 1
n 0
n 0
x12 n x22 n
r12 j
x1
11
r
функция автокорреляции
1 N 1
r11 j x1 n x1 n j
N n 0
коэффициент автокорреляции
r j
, 11 1
r11 0
11 j 11
0 r 0
x2
11
,
12 1
4.
Циклическая и линейная корреляцииx1 x 2 x3 x4
r(j)
x={x1,x2,x3,x4}
y3 y1 y2 y3 x1y3+x2y1+x3y2+x4y3
y={y1,y2,y3}
y1 y2 y3 y1 x1y1+x2y2+x3y3+x4y1
Циклическая корреляция
периодична с периодом,
равным длине более короткой
реализации
y2 y3 y1 y2 x1y2+x2y3+x3y1+x4y2
y3 y1 y2 y3 x1y3+x2y1+x3y2+x4y3
y1 y2 y3 y1 x1y1+x2y2+x3y3+x4y1
Для получения линейной корреляции
последовательности необходимо
дополнить нулями:
x1 x2 x3 x4
x={x1,x2,x3,x4,0,0}
y3
y1 y2 y3
N1 – длина первого вектора
N2 – длина второго вектора
x1y1+x2y2+x3y3
y2 y3
y3 x1y2+x2y3
y2 y3 x1y3
y={y1,y2,y3,0,0,0}
Длина конечного вектора: N1+N2-1
r(j)
y1 y2 y3 x4y1
y1 y2 y3
y1 y2 y3
y1 y2 y3
x3y1+x4y2
x2y1+x3y2+x4y3
x1y1+x2y2+x3y3
5.
Быстрая корреляцияРасчет быстрой корреляции методом БПФ
Теорема о корреляции:
r12 j DFT 1 X 1 k X 2 k
Это выражение для циклической корреляции. Для получения линейной
корреляции нужно использовать дополняющие нули.
Расчет быстрой корреляции рекурсивным методом
1 N 1
r12 x1 n x 2 n
N n 0
(новое значение) = (предыдущее значение) +
+1/N(произведение двух новых членов)-1/N(произведение первых двух членов)
6.
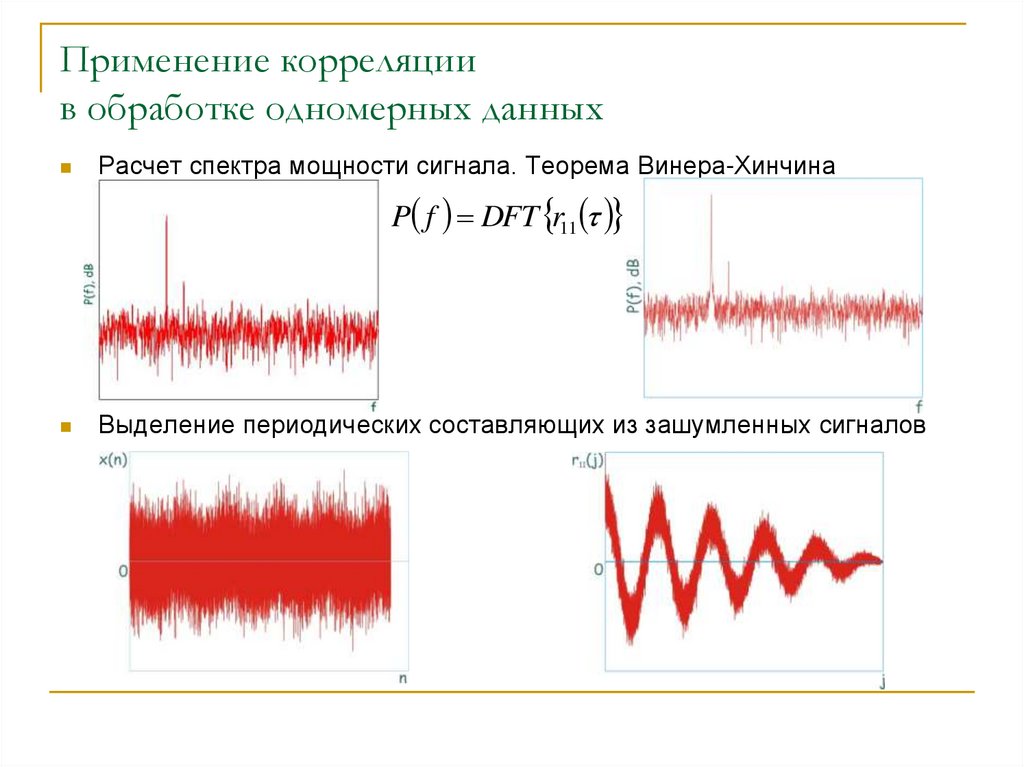
Применение корреляциив обработке одномерных данных
Расчет спектра мощности сигнала. Теорема Винера-Хинчина
P f DFT r11
Выделение периодических составляющих из зашумленных сигналов
7.
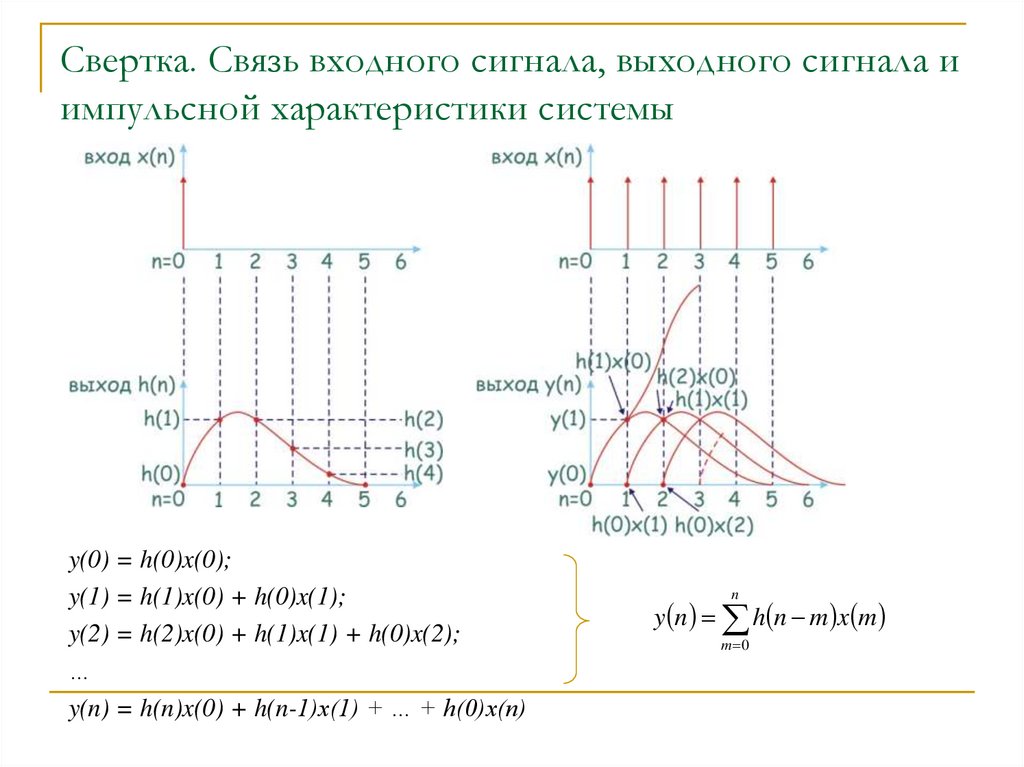
Свертка. Связь входного сигнала, выходного сигнала иимпульсной характеристики системы
y(0) = h(0)x(0);
y(1) = h(1)x(0) + h(0)x(1);
y(2) = h(2)x(0) + h(1)x(1) + h(0)x(2);
…
y(n) = h(n)x(0) + h(n-1)x(1) + … + h(0)x(n)
n
y n h n m x m
m 0
8.
Графическая интерпретация операции сверткиx(m)
h(m)
x(m)
h(t-m)
x(m)
h(-m)
9.
Свертка во временной и частотной областяхТеорема о свертке
X f DFT x n
Y f DFT y n
H f DFT h n
y n x n h n
y n x n h n
Y f X f H f
Y f X f H f
Свойства свертки
Коммутативность
x1 n x2 n x2 n x1 n
Дистрибутивность
x1 n x2 n x3 n x1 n x2 n x1 n x3 n
Ассоциативность
x1 n x2 n x3 n x1 n x2 n x3 n
10.
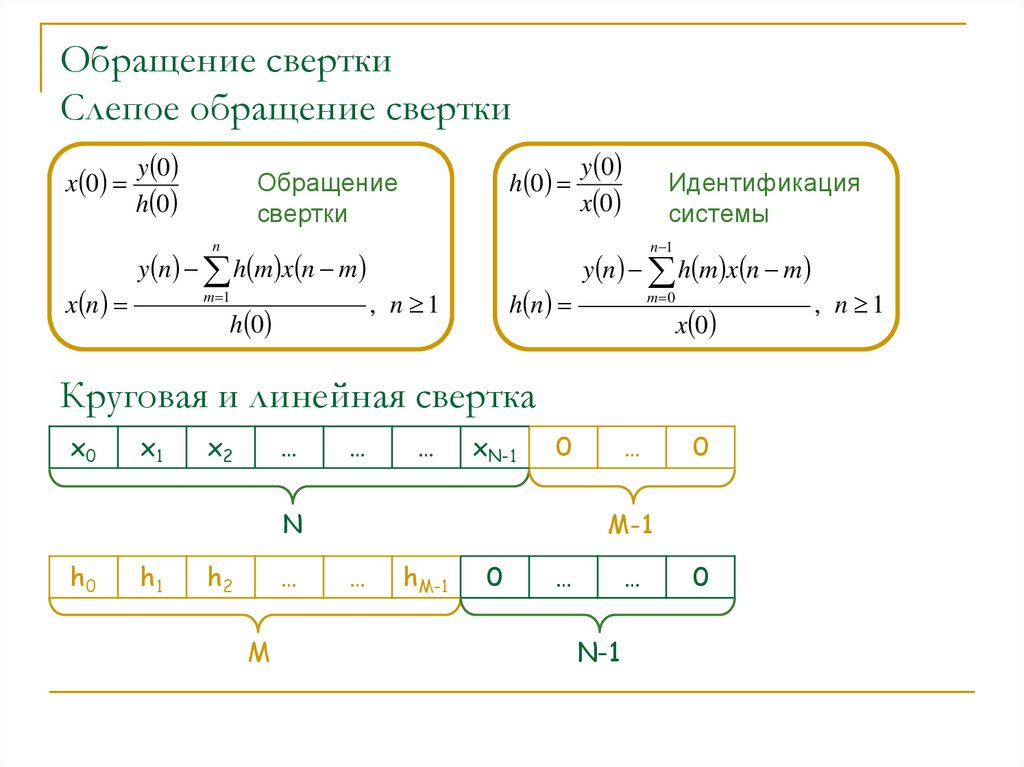
Обращение сверткиСлепое обращение свертки
x 0
y 0
h 0
h 0
Обращение
свертки
x n
m 1
h 0
Идентификация
системы
n 1
n
y n h m x n m
y 0
x 0
h n
, n 1
y n h m x n m
m 0
x 0
Круговая и линейная свертка
x0
x1
x2
…
…
…
xN-1
0
N
h0
h1
h2
…
M
…
0
M-1
…
hM-1
0
…
…
N-1
0
, n 1
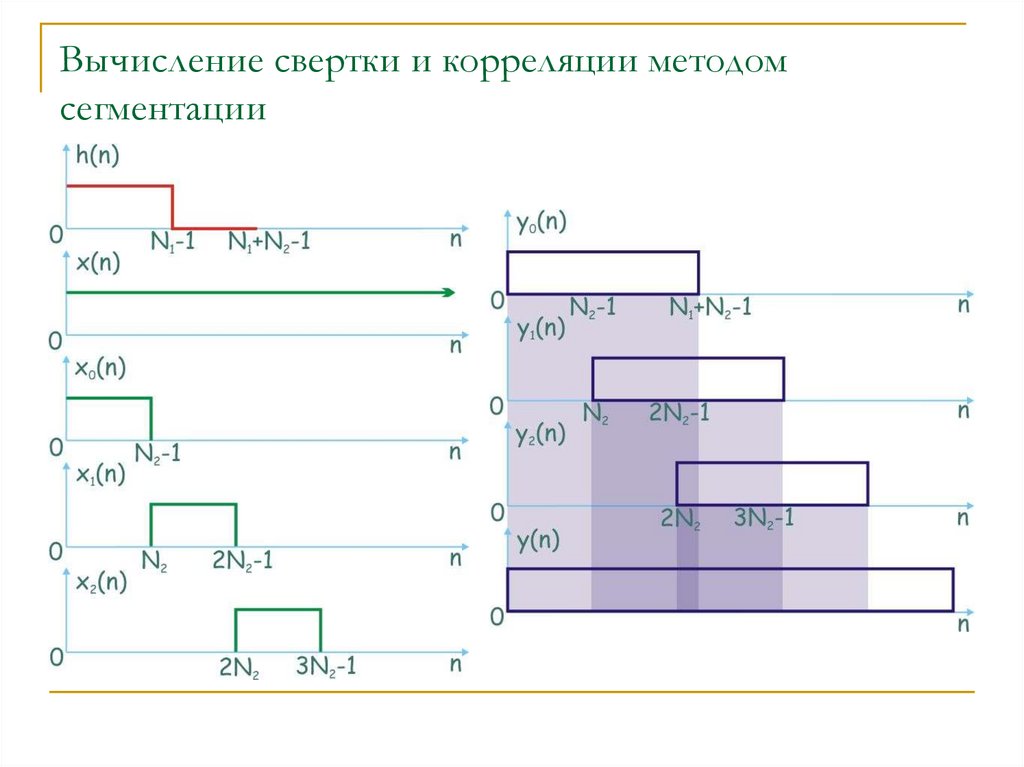
11.
Вычисление свертки и корреляции методомсегментации






 Математика
Математика








