Переходный процесс в цепи с R-L- C элементами

1.

Переходный процесс
в цепи с R-L- C элементами

2.

Переходный процесс в цепи с R-L-C элементами
1) ННУ t = 0–
при t = 0+
iL (0 ) 0
uC (0 ) 0
uC (0 ) uC (0 ) 0
iL (0 ) iL (0 ) 0
t
di (0 )
1
L
Ri (0 ) i (0 )dt E
dt
C
0
di (0 ) Е
dt
L
Зависимые
НУ

3.

2) После коммутации
di
1
L Ri idt E
dt
C
2
d i
di 1
L 2 R i 0
dt C 3) Характеристическое
dt
уравнение
1
R
1
2
Lp Rp 0 p p
0
C
L
LC
2
Корни характеристического
уравнения
2
R
1
R
p1,2
2L
LC
2L

4.

2
R
1
R
p1,2
2L
LC
2L
2
2
0
p1,2
R
Затухание
2L
Угловая частота
0
1
LC
Критическое сопротивление
2
Rкр
1
0
LC
2L
Rкр 2 L
C
2
Волновое сопротивление
L
C

5.

При R = RКР
Свободная составляющая
R
p
2L
icв e pt ( А1 A2t )
При R > RКР
p1,2
2
2
0
При R < RКР
iсв A1e p1t A2 e p2t
p1, 2 j св
св
2
2
0
4) Принужденная
составляющая
iпр 0
5) Общее решение
i icв

6.

6) Найдем Ai для R>RКР
i A1e
p1t
A2 e
p2t
di
p1t
p2t
A1 p1e A2 p2 e
dt
при t = 0+
i (0 ) A1 A2 0
p1,2 2 02
di
E
(0 ) A1 p1 A2 p2
dt
L
E
E
A1 A2
L( p1 p2 ) 2 L 2 2
0

7.

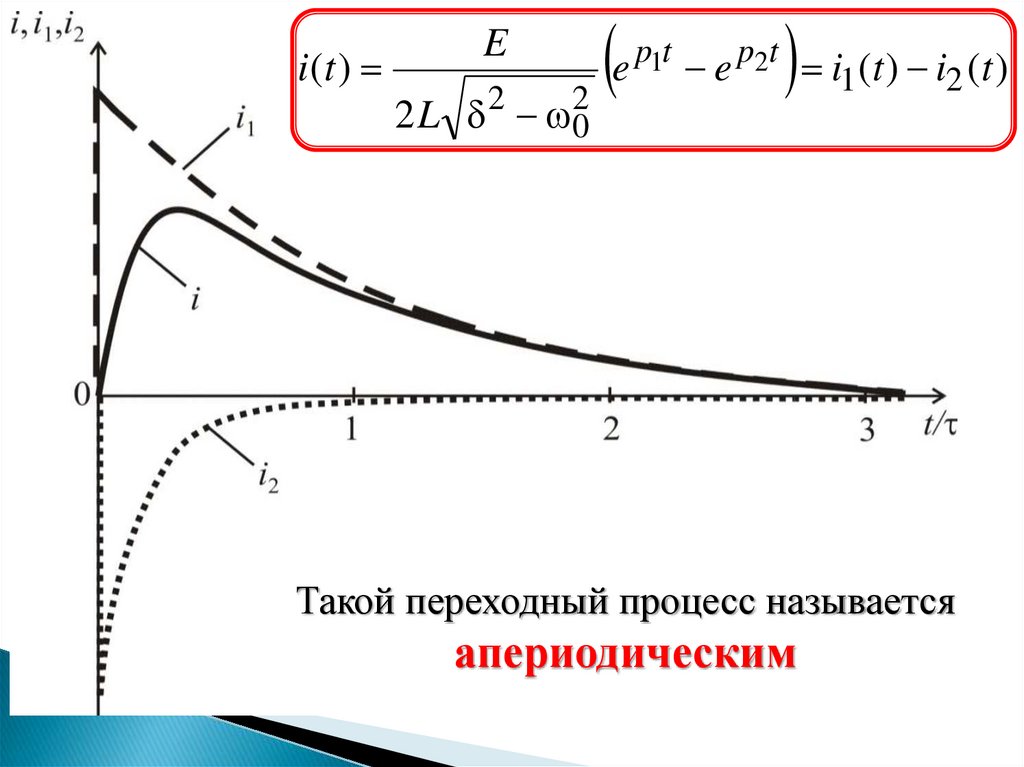
i (t )
E
e p t e p t i1 (t ) i2 (t )
2
1
2
2 L 2 0
Такой переходный процесс называется
апериодическим

8.

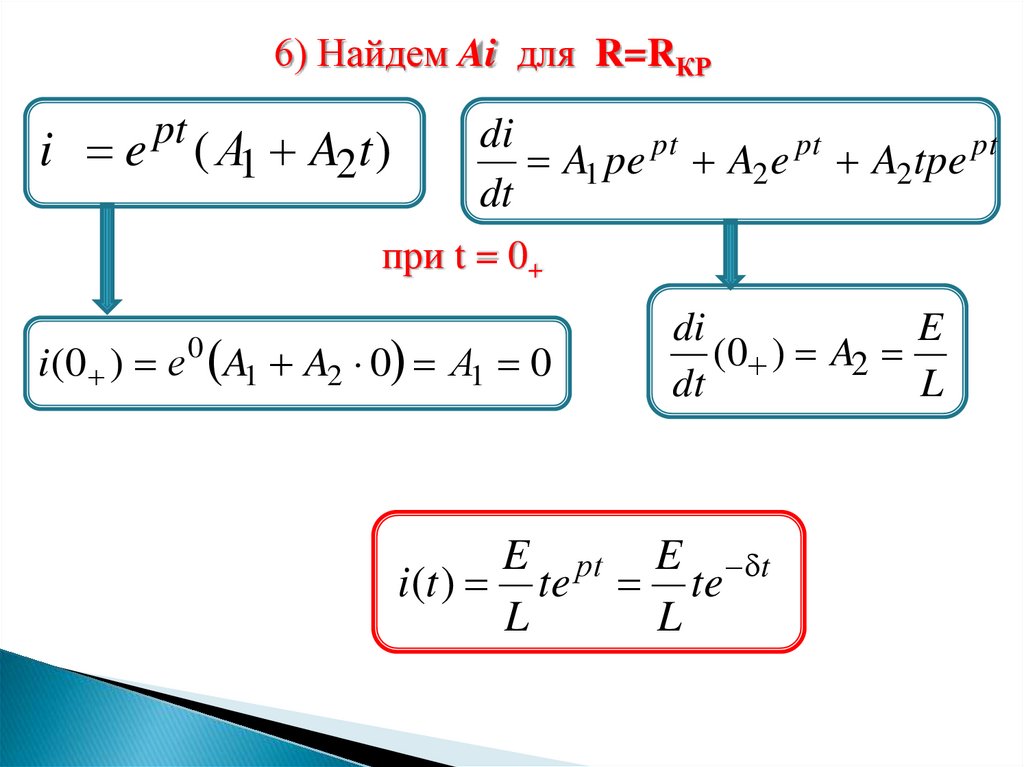
6) Найдем Ai для R=RКР
pt
i e ( А1 A2t )
di
A1 pe pt A2 e pt A2tpe pt
dt
при t = 0+
i(0 ) е A1 A2 0 А1 0
0
di
E
(0 ) A2
dt
L
E рt E t
i (t ) te te
L
L

9.

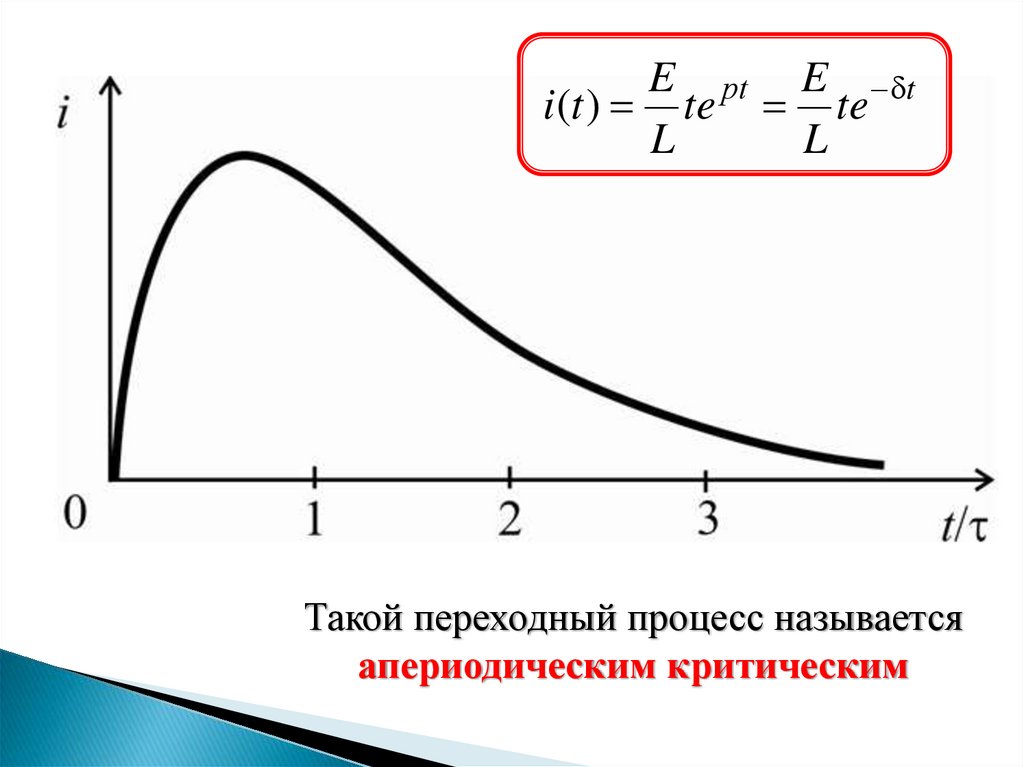
E рt E t
i (t ) te te
L
L
Такой переходный процесс называется
апериодическим критическим

10.

t
Ee
e
i (t )
L св
j св t
e
2j
j св t
t
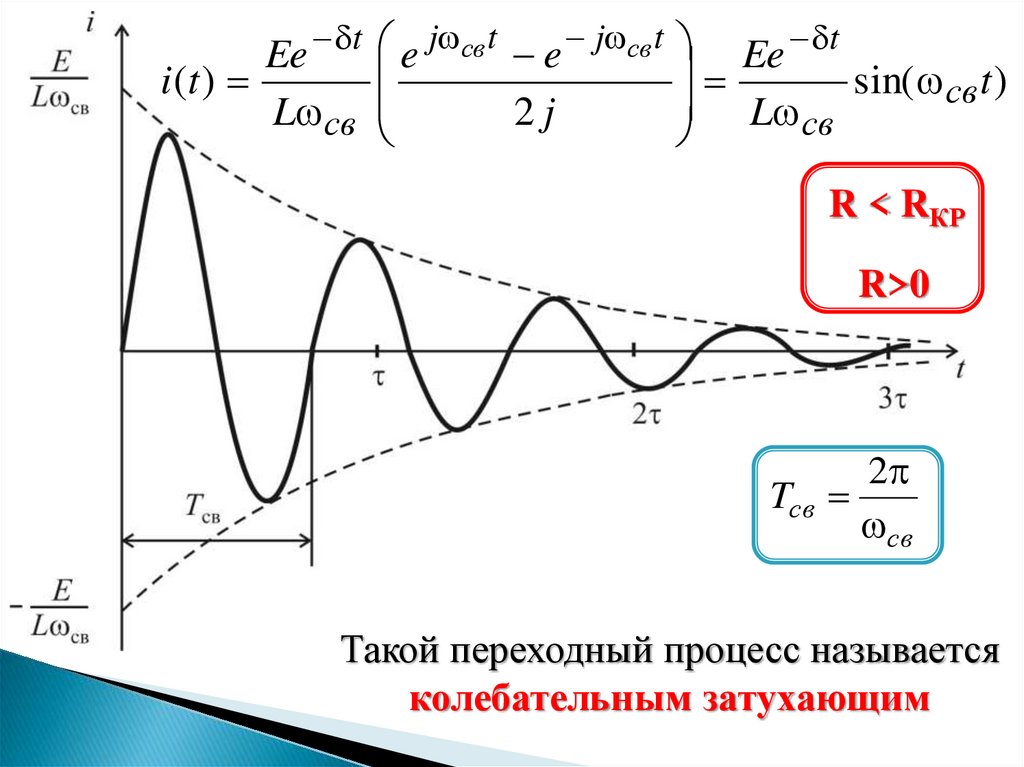
Ee
sin( св t )
L св
R < RКР
R>0
2
Tсв
св
Такой переходный процесс называется
колебательным затухающим

11.

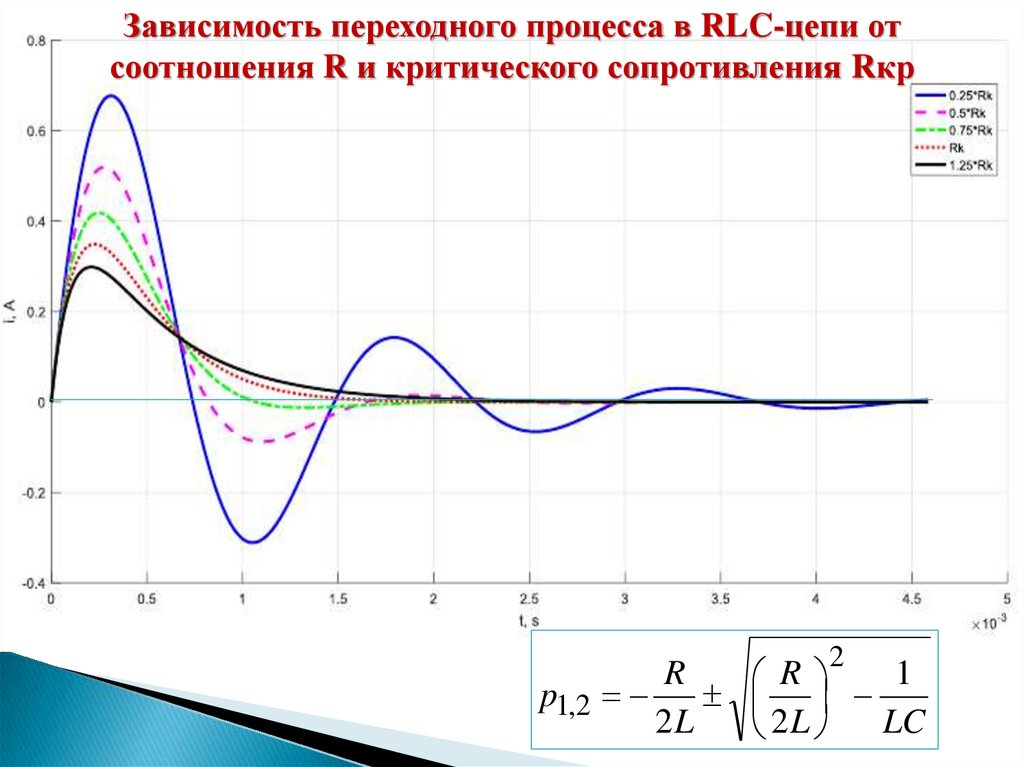
Зависимость переходного процесса в RLC-цепи от
соотношения R и критического сопротивления Rкр
p1,2
2
R
1
R
2L
LC
2L

12.

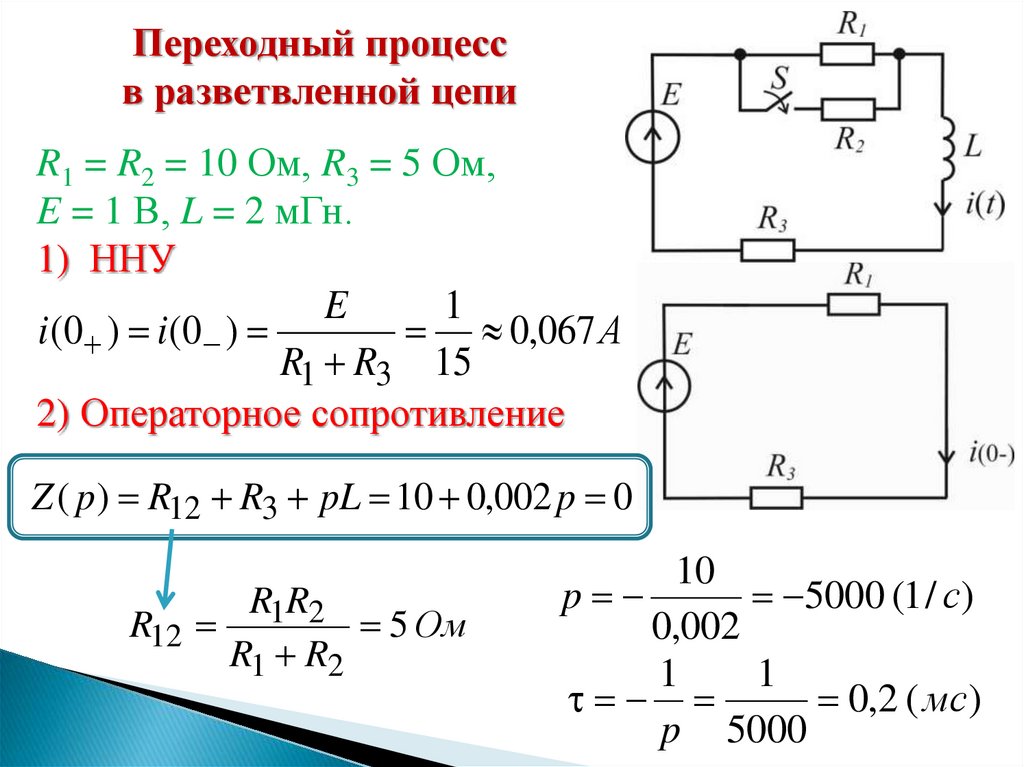
Переходный процесс
в разветвленной цепи
R1 = R2 = 10 Ом, R3 = 5 Ом,
E = 1 В, L = 2 мГн.
1) ННУ
E
1
i (0 ) i (0 )
0,067 А
R1 R3 15
2) Операторное сопротивление
Z ( p ) R12 R3 pL 10 0,002 p 0
R1R2
R12
5 Ом
R1 R2
10
p
5000 (1 / с )
0,002
1
1
0,2 ( мс)
p 5000

13.

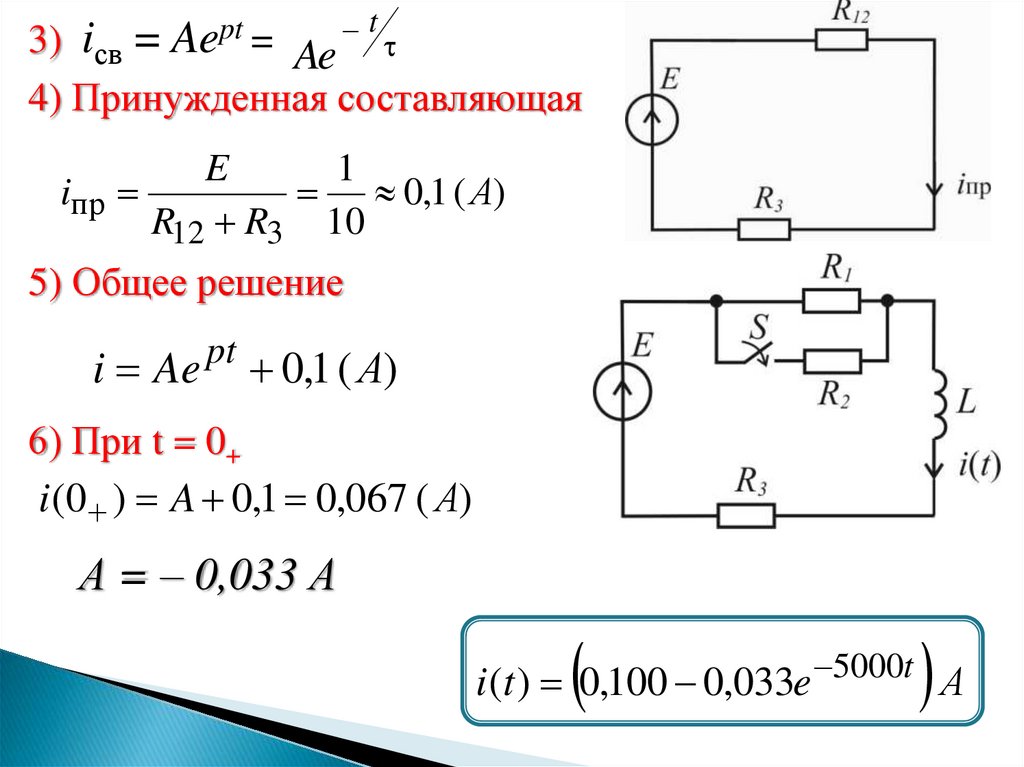
= Aept =
t
3) iсв
Ae
4) Принужденная составляющая
E
1
iпр
0,1 ( А)
R12 R3 10
5) Общее решение
i Ae
pt
0,1 ( А)
6) При t = 0+
i (0 ) A 0,1 0,067 ( А)
А = – 0,033 А
i (t ) 0,100 0,033e
5000t
А

14.

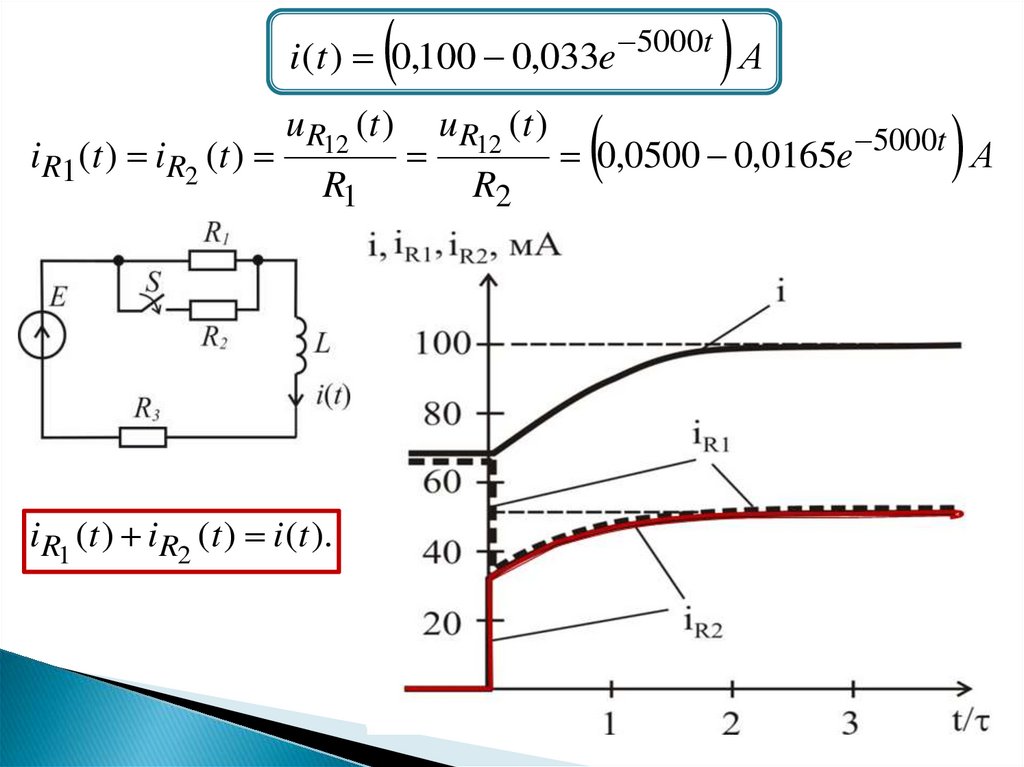
i (t ) 0,100 0,033e 5000t А
iR1 (t ) iR2 (t )
u R12 (t )
R1
iR1 (t ) iR2 (t ) i (t ).
u R12 (t )
R2
0,0500 0,0165e 5000t А

15.

i (t ) 0,100 0,033e 5000t А
di
u L (t ) L 0,002 ( 0.033) 5000 e 5000t
dt
0,330e
5000t
В
u R12 (t ) u R3 (t ) R12 i (t )
5 0,100 0,033 e 5000t
0,500 0,165 e 5000t В

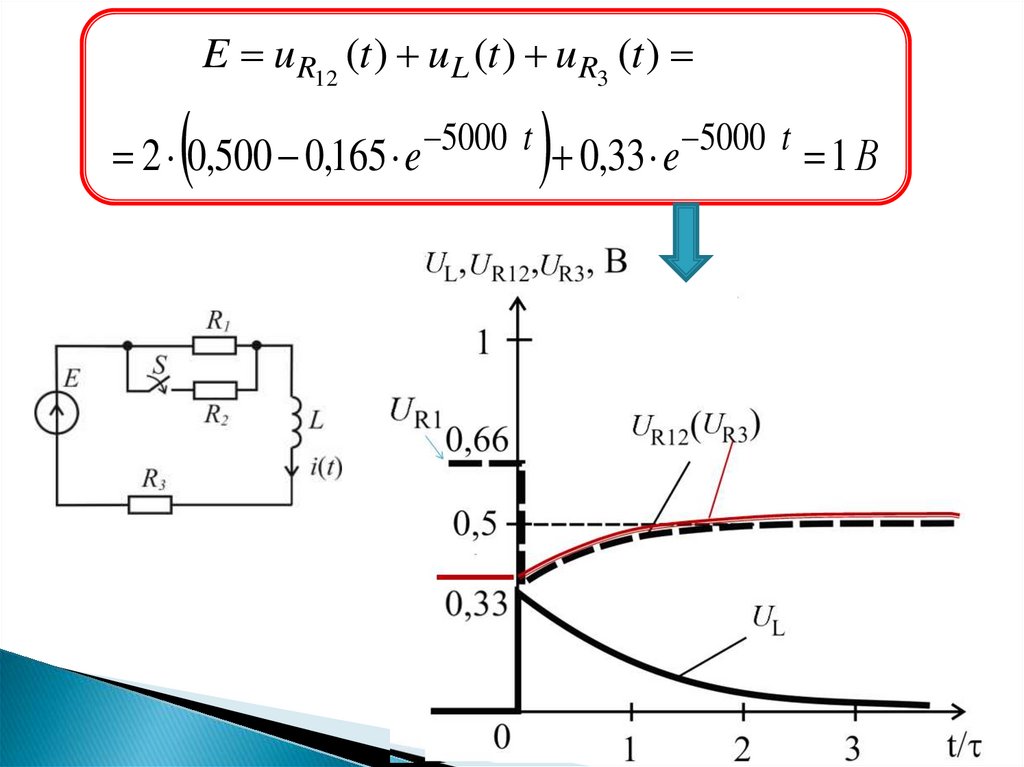
16.

E u R12 (t ) u L (t ) u R3 (t )
2 0,500 0,165 e
5000 t
0,33 e 5000 t 1 В

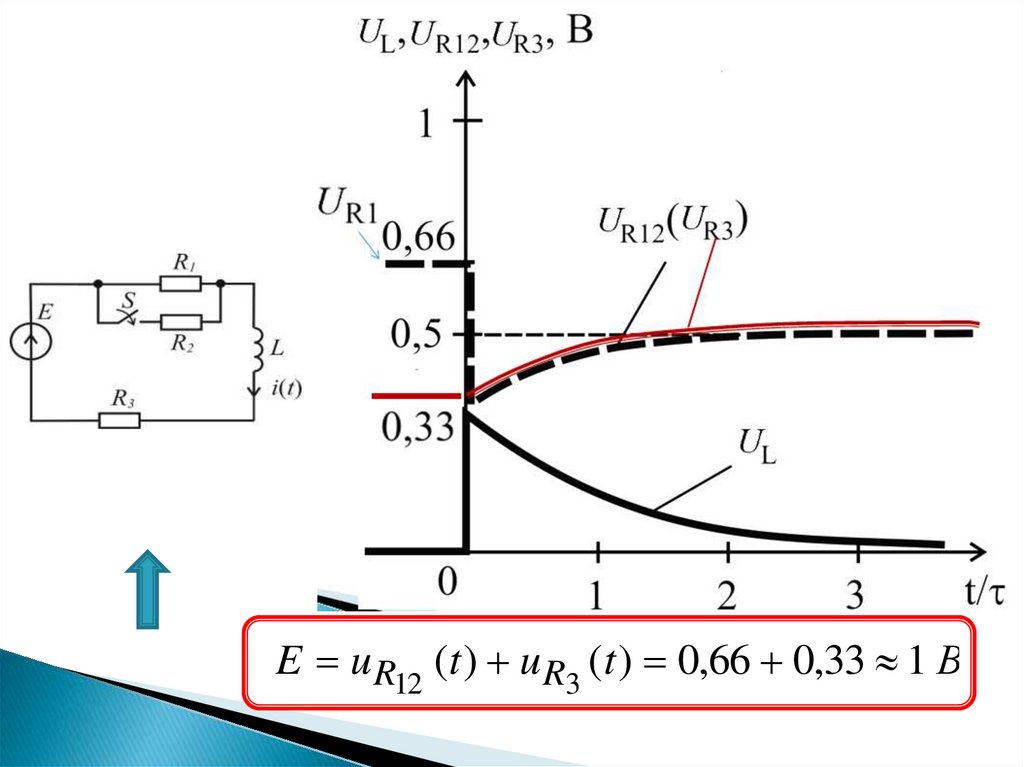
17.

E u R12 (t ) u R3 (t ) 0,66 0,33 1 В

18.

Особенности расчета переходных процессов в
нелинейных цепях
Для расчета переходных процессов в нелинейных цепях:
• нельзя применять классический метод расчета;
• нельзя применять операторный метод расчета;
• требуется определять динамических характеристик
нелинейных элементов, зависящих от происходящих в них
динамических процессов.
В различные интервалы
времени переходный процесс
в нелинейной цепи может
протекать с различной
скоростью.

19.

Методы расчета переходных процессов
нелинейный электрических цепей
можно разделить на три группы:
1) аналитические методы:
метод условной линеаризации
метод аналитической аппроксимации
метод кусочно-линейной аппроксимации
2) графические методы
3) численные методы

20.

Метод условной
линеаризации
1) ННУ. Определяем независимые начальные условия в цепи
до коммутации : iL(0_) или uC(0_ ) .
2) ЗНУ. Определяем искомую величину при t(0+ ): – i(0 +)
или u(0 +) .
3) Из расчета установившегося режима после коммутации
находим установившиеся значения при t = ∞: iуст или uуст

21.

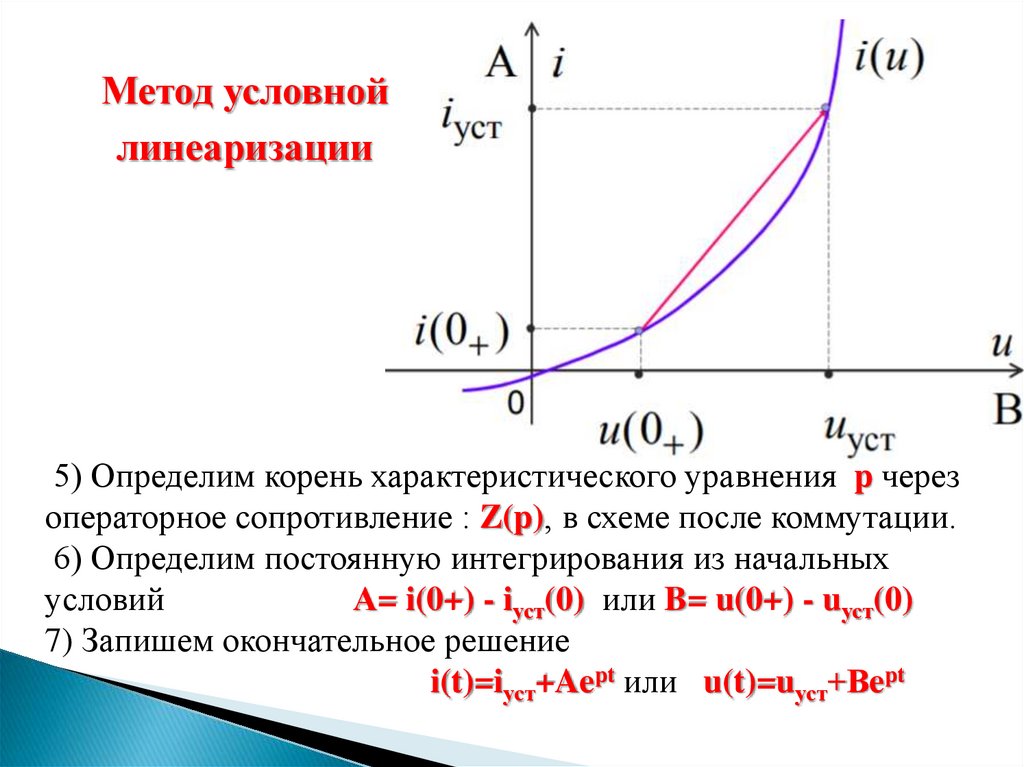
Метод условной
линеаризации
4) Линеаризуем участок
характеристики НЭ

22.

Метод условной
линеаризации
5) Определим корень характеристического уравнения p через
операторное сопротивление : Z(p), в схеме после коммутации.
6) Определим постоянную интегрирования из начальных
условий
А= i(0+) - iуст(0) или B= u(0+) - uуст(0)
7) Запишем окончательное решение
i(t)=iуст+Aept или u(t)=uуст+Вept