Переходные процессы в цепях с сосредоточенными параметрами

1.

Переходные процессы в цепях с сосредоточенными параметрами
Стационарный (установившийся) режим – это режим при котором распределение электромагнитной
энергии между элементами цепи постоянно (цепи постоянного тока) или меняется во времени по
периодическому закону (цепи синусоидального и периодического несинусоидального тока.
Переходные процессы – это явление изменения во времени напряжений, токов или
производных от них величин, обусловленное переходом от одного стационарного
состояния цепи к другому.
Коммутациями называют скачкообразные изменения элементов цепи.

2.

Законы коммутации
WM ( 0 )
Энергия, накопленная в катушке индуктивности:
L i(20 )
2
L i(20 )
WM ( 0 )
2
(0 ) (0 )
Потокосцепление
1й закон коммутации – ток в катушке индуктивности скачком измениться не может
i L (0 ) i L (0 )
Энергия, накопленная конденсатором:
Заряд
WЭ( 0 )
C u(20 )
2
C u(20 )
2
Q( 0 ) Q( 0 )
2й закон коммутации – напряжение на емкости скачком измениться не может
u C (0 ) u C (0 )
WЭ( 0 )

3.

Классический метод расчета переходных процессов
Подключение последовательной RL-цепи к источнику постоянного напряжения
u L uR U
i iпр iсв
i пр
i св
i пр
U
R
- принужденная составляющая
- свободная составляющая
L
di
iR U
dt

4.

di
L iR 0
dt
iсв Ae pt
А – постоянная интегрирования
р – корень характеристического уравнения
Характеристическое уравнение:
iсв Ae
R
R
t
L
t
U
i iпр iсв Ae L
R
Начальные условия:
U
0 A
R
1 L
p R
R
p
L
pL R 0
i(0 ) i L (0 ) i L (0 ) 0
U
A
R
- постоянная времени
R
U U Lt
i e
R R

5.

R
U U Lt
i e
R R
U R iR U (1 e
R
t
L
R
)
t
di
U L L Ue L
dt

6.

Короткое замыкание последовательной RL - цепи
Подключение последовательной RL-цепи к источнику
синусоидального напряжения

7.

Подключение последовательной RС-цепи к источнику постоянного напряжения
u R uC U
U R iR
duC
iC C
dt
duC
RC
uC U
dt
uC uC пр uC св
uC пр U
RC
du C
uC 0
dt
u C св Ae pt
Характеристическое уравнение:
uC U Ae
1
t
RC
RCp 1 0
p
1
RC

8.

uC U Ae
1
t
RC
Начальные условия:
A U
0 U A
uC U Ue
1
RC
p
u C (0 ) u C (0 ) 0
1
t
RC
- постоянная времени
1
du C
1 RC t U RC1 t
iC C
CU (
)e
e
dt
RC
R
U R iR Ue
1
t
RC
Uc
U
U/R
Ur
t

9.

Разрядка емкости через конденсатор

10.

Свободные колебания в последовательной RLC-цепи
Начальные условия:
SA
R
uC (0 ) U
UR
С
UL
Uc
U
iL (0 ) 0
L
i
uL uR uc 0
L
di
iR uc 0
dt
iC C
duC
dt
d 2 u c R du c
1
uc 0
dt
L dt
LC
R
2
L
1
0
LC
p 2 2 p 02 0
p1,2 2 02

11.

1 вариант
0
R
2L
p1 2 02
u C A1e p1t A2 e p2t
1
LC
R 2
L
C
du C
CA1e p1t CA2 e p2t
dt
i,u
Uo
uc
0
t
uL
-Uo
1
Q
2
- отрицательные, действительные числа
p2 2 02
i C
R 2
i
Свободный процесс носит апериодический характер
uL L
di
dt

12.

2 вариант
0
R
2L
1
LC
1
Q
2
p1 p2
Свободный процесс носит граничный апериодический характер

13.

3 вариант
0
Q
1
2
2
R2
C 0 1 2 0 1 2
0
4
2
0
С
2
-собственная частота последовательного колебательного контура
p1 j C
p 2 j C
uC A1e t e j Ct A2 e
t
arcsin
где
i
U
C L
e
t
e j Ct U
0
e
C
t
sin( C t )
c
0
sin( C t )
Свободный процесс носит колебательный характер

14.

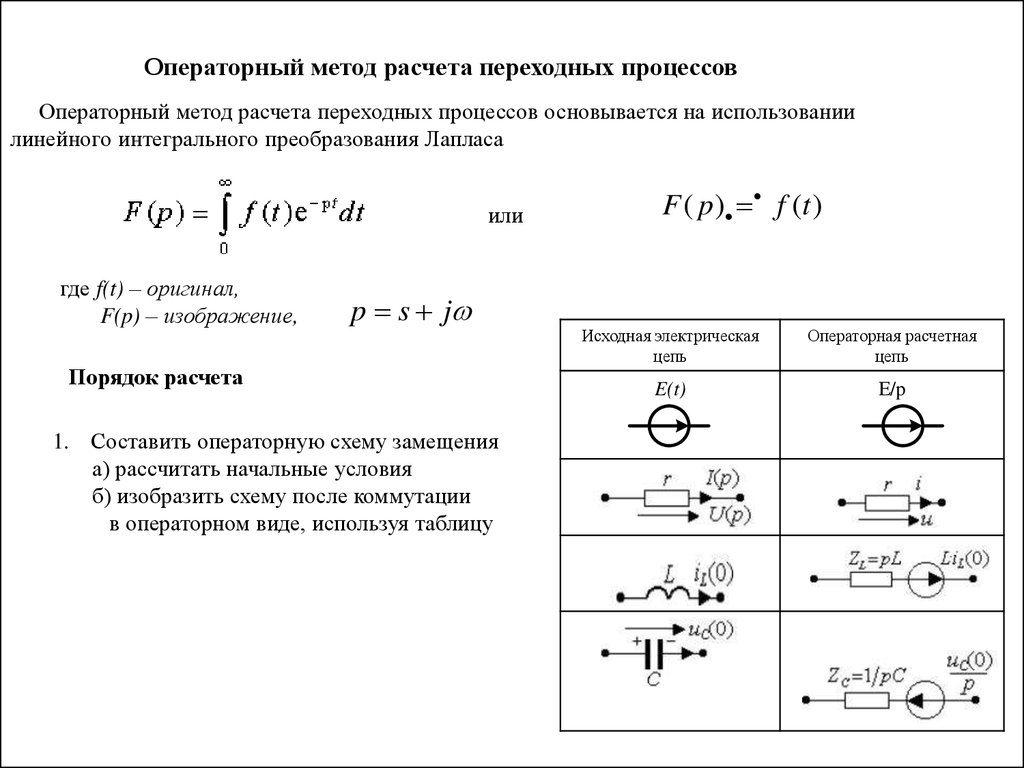
Операторный метод расчета переходных процессов
Операторный метод расчета переходных процессов основывается на использовании
линейного интегрального преобразования Лапласа
или
где f(t) – оригинал,
F(p) – изображение,
p s j
Порядок расчета
1. Составить операторную схему замещения
а) рассчитать начальные условия
б) изобразить схему после коммутации
в операторном виде, используя таблицу
F ( p ) f (t )
Исходная электрическая
цепь
Операторная расчетная
цепь
E(t)
E/p

15.

2. Рассчитать операторную схему, используя методы теории электрических цепей.
3. Определить оригинал по изображению, используя теорему разложения.
Если
F ( p)
F1 ( p )
F2 ( p )
, то найти оригинал можно по формуле:
n
F1 ( p к ) pкt
e
'
к 1 F2 ( p к )
f (t )
где
pk
- корни уравнения
F2 ( р) 0

16.

Пример расчета
Для цепи второго порядка найти операторным методом ток после размыкания ключа SА.
Параметры цепи: E=40 B; r =40 Ом; L = 1 Гн; C = 1/300 Ф.
Решение задачи начинаем с изображения операторной цепи,
которая соответствует послекоммутационному состоянию цепи .
Начальные условия для внутренних источников энергии находятся
для момента времени t = 0- так же, как это было сделано при решении задачи
классическим методом: iL (0-) = E/r = 1 A; uC(0-) = E = 40 B.
В операторной одноконтурной цепи протекает операторный ток I(p)
под действием операторных источников напряжения
SA
Е
С
r
L

17.

Формально рассматривая эту цепь как цепь постоянного тока, найдем
После подстановки численных значений параметров получим
Приравнивая нулю знаменатель, найдем корни
Следует заметить, что знаменатель совпадает с характеристическим уравнением для
исследуемой цепи.. Далее найдем производную знаменателя
Применим Теорему разложения и найдем оригинал тока как функцию времени

18.

e t 10e 200t 1 t
E p
10
p
E p 200
.
E p
10
p 200
E p 10 sin p 200
E p
10p
p 2 2002
Яким є операторне зображення цього
джерела напруги?