Похожие презентации:
Переходные процессы в линейных электрических цепях
1.
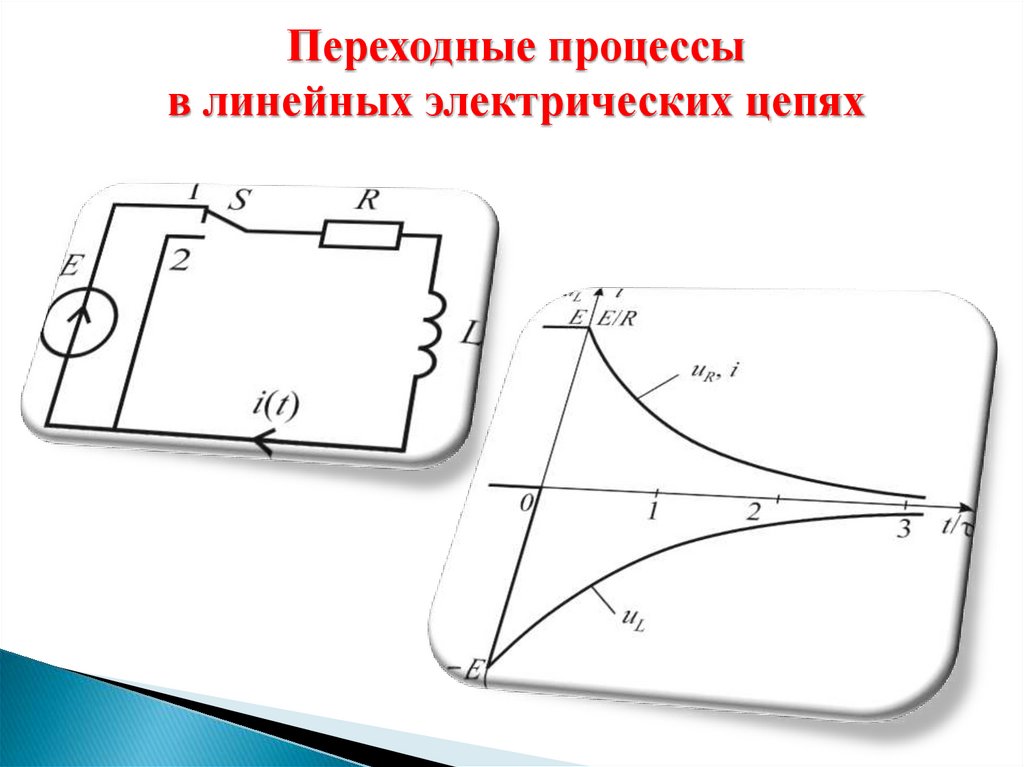
Переходные процессыв линейных электрических цепях
2.
Коммутация скачкообразное изменения структурыцепи, параметров ее элементов, а также подключением
или отключением источников энергии.
Момент времени непосредственно до коммутации t = 0–
Момент времени сразу же после коммутации t = 0+
Ключевые элементы
Замыкающий Размыкающий Переключающий
3.
законкоммутации. Если
в процессе
коммутации индуктивность элемента не изменяется, то
значение тока в ней до коммутации iL(0–) равно
значению тока сразу же после коммутации iL(0+), а
затем плавно изменяется от этого значения
1
iL(0+) = iL(0–)
закон
коммутации.
при L = const.
Если в процессе
коммутации емкость элемента не изменяется, то
значение напряжения в ней до коммутации uC(0–)
равно значению напряжения сразу же после
коммутации uC(0+), а затем плавно изменяется от этого
значения
uC(0+) = uC(0–)
при C = const.
2
4.
Значения токов и напряжений в момент времениt = 0– называются начальными значениями.
Независимые начальные значения: ННУ
iL(0–) , uC(0–).
Зависимые начальные значения: ЗНУ
uL(0–) , iC(0–), uR(0–) , iR(0–).
Установившиеся значения
значения токов и напряжений в цепи после
переходного процесса, т.е. при t .
.
5.
Классический метод расчета переходных процессовn
an
d i
dt
n
an 1
d
n 1
i
dt
n 1
... a0i f (t )
i iпр icв
an
d nicв
dt
n
an 1
d n 1icв
dt
n 1
... a0icв 0
6.
and nicв
dt
n
an 1
d n 1icв
dt
n 1
...a0icв 0
Характеристическое уравнение
an p an 1 p
n
n 1
... a1 p a0 0
Для простых корней
icв An e
pn t
An 1e
p n 1t
Для кратных корней
icв An t
n 1
An 1t
n 2
... A1e
... A1 e
p1t
pt
7.
d nicвd n 1icв
an n an 1 n 1 ... a0icв f (t )
dt
dt
Общее решение дифференциального уравнения
Для простых корней
i iпр An e pnt An 1e pn 1t ... A1e p1t
Для кратных корней
i iпр An t n 1 An 1t n 2 ... A1 e pt
8.
Для нахождения постоянных интегрирования Аiзаписывают выражения для искомого тока i(t) и его
(n 1) производных в момент t = 0+.
Для простых корней
An An 1 ... A1 i (0 ) iпр ;
di (0 ) di пр
;
pn An pn 1 An 1 ... p1 A1
dt
dt
n 1
n 1
d
i пр
d i (0 )
n 1
n 1
n 1
pn An pn 1 An 1 ... p1 A1
.
dt n 1
dt n 1
9.
A=CA1
A
A= 2
...
An
Решение системы
A = 1 C
1
p1
p1n 1
1
p2 ...
...
p2n 1
1
pn
pnn 1
i (0 ) iпр
di (0 ) di пр
dt
dt
C=
...
n 1
n 1
d
i
пр
d i (0 )
dt n 1
dt n 1
10.
Рекомендуемую последовательность расчетаклассическим методом
1. Анализ цепи до коммутации и определение
независимых начальных условий;
2. Составление гармонических уравнений Кирхгофа для
цепи после коммутации;
3. Составление и решение характеристического уравнения.
Определение свободной составляющей решения;
4. Составление уравнений Кирхгофа для цепи после
коммутации и определение принужденной составляющей
решения;
5. Нахождение общего вида решения в виде суммы
принужденной и свободной составляющих;
6. Определение постоянных интегрирования.
11.
Переходный процесс в цепи с R и L элементами1) До коммутации i(0–) = 0
i(0+) = i(0–) = 0.
2) После коммутации:
di
uL (t ) uR (t ) L Ri E
dt
12.
Переходный процесс в цепи с R и L элементамиdi
u L (t ) u R (t ) L Ri E
dt
3) Характеристическое
уравнение:
Lp + R = 0
R
p
L
t
iсв Ae pt Aе
1 L
p R
13.
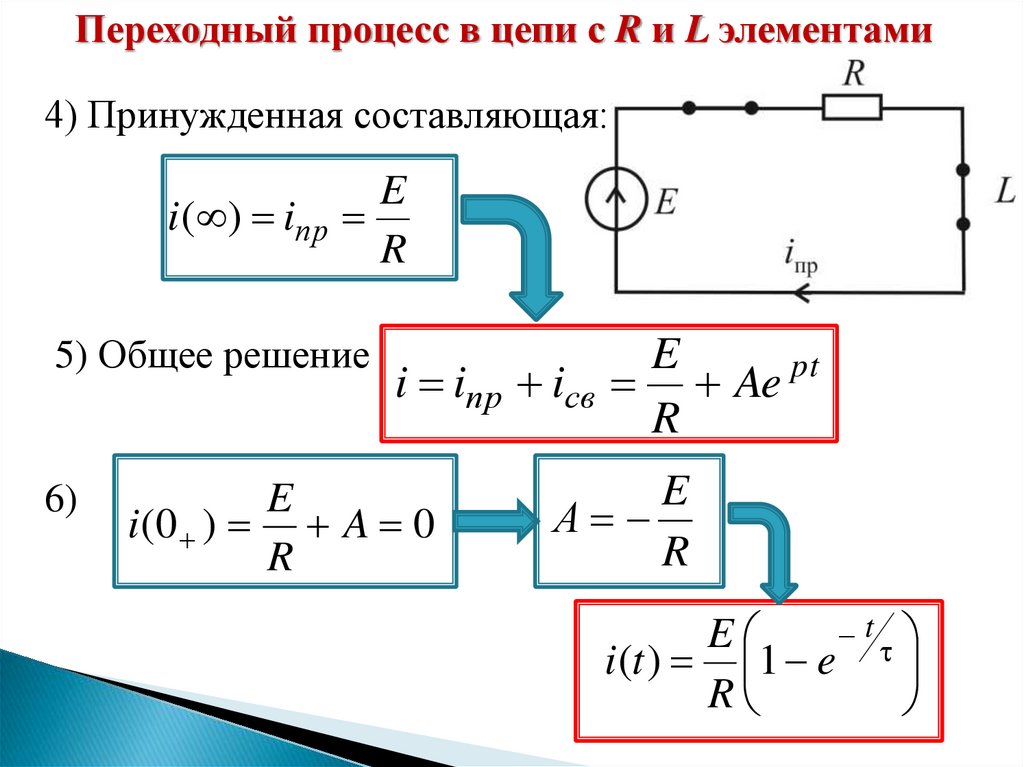
Переходный процесс в цепи с R и L элементами4) Принужденная составляющая:
E
i ( ) iпр
R
5) Общее решение
6)
E
i iпр iсв Ae pt
R
E
i (0 ) A 0
R
E
А
R
t
E
i (t ) 1 e
R
14.
tE
i (t ) 1 e
R
15.
E 1 tE R t
t
di
L
Ee .
u L (t ) L L e
e
dt
R
R L
t
E
i (t ) 1 e
R
u L (t ) u R (t )
Ee
t
Е E
t
Е
t
u R (t ) Ri E 1 e
16.
Комплекс полного сопотивленияZ = j L + R
Операторное сопротивление
Z(p) = pL + R
Характеристическое уравнение цепи
pL + R = 0
17.
1)E
i (0 ) i (0 )
R
3)
pL + R = 0
R
p
L
2)
di
L Ri 0
dt
iсв Ae
pt
A
t
18.
4) i ( ) i 0пр
5)
6)
i iпр iсв Ae
E
i (0 ) A
R
pt
E
А
R
E t
i (t ) e
R
19.
E ti (t ) e
R
u R (t ) Ri (t ) Ee
t
u L (t ) u R (t )
Ee
t
Eе
t
0
t
di
E R t
u L (t ) L L e
Ee
dt
R L
20.
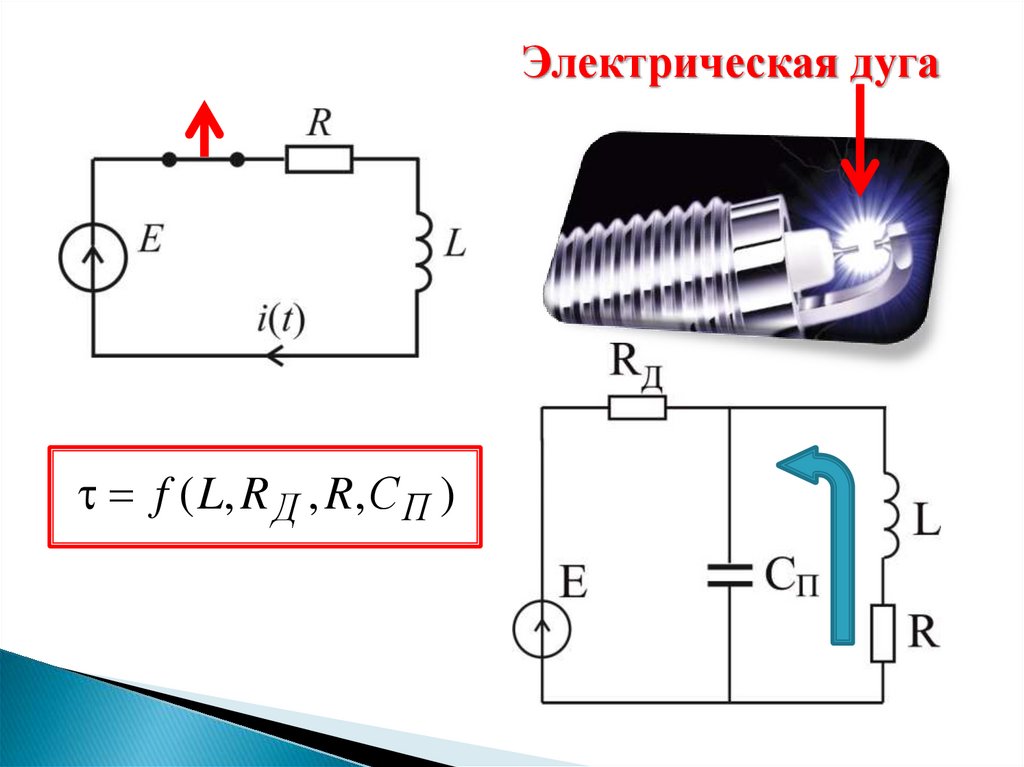
Электрическая дугаf ( L, R Д , R, С П )
21.
Ei (0 ) i (0 )
R
RV
Е
uV (0 ) RV i(0 ) RV E
R
R
u L (0 ) Ri(0 ) RV i(0 ) 0
RV
u L (0 ) ( R RV )i(0 ) E 1
R
RV >> R
Во избежание возникновения больших
перенапряжений при отключении цепей
постоянного тока с большой индуктивностью
(например, обмоток возбуждения генераторов
постоянного тока) эти цепи предварительно
замыкают на малое сопротивление.
22.
e Em sin( t е )Ток после коммутации
i iпр iсв iпр Ae
iпр
Em
R 2 ( L) 2
pt
sin( t e ) I m sin( t e )
L
arctg
R
23.
e Em sin( t е )Ток до коммутации и сразу
же после коммутации = 0
i (0 _) i (0 ) I m sin( е ) A 0
А I m sin( е )
i iпр iсв I m sin( t e ) I m sin( e )e
t /
Полный ток в цепи после коммутации
24.
25.
= e +(k+1/2)(k = 0, 1, 2 …)
26.
= e +(k-1/2)27.
e= +k(k = 0, 1, 2 …)
28.
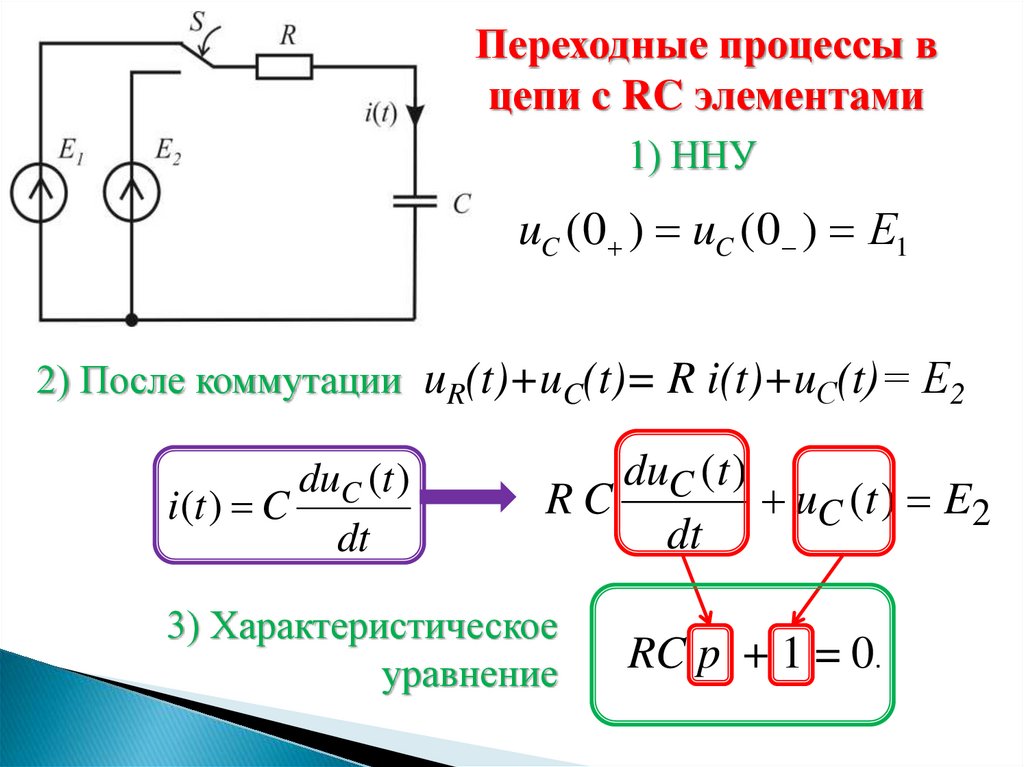
Переходные процессы вцепи c RC элементами
1) ННУ
uC (0 ) uC (0 ) Е1
2) После коммутации uR(t)+uC(t)= R i(t)+uС(t)= Е2
duC (t )
i(t ) C
dt
duC (t )
RC
uC (t ) E2
dt
3) Характеристическое
уравнение
RC p + 1 = 0.
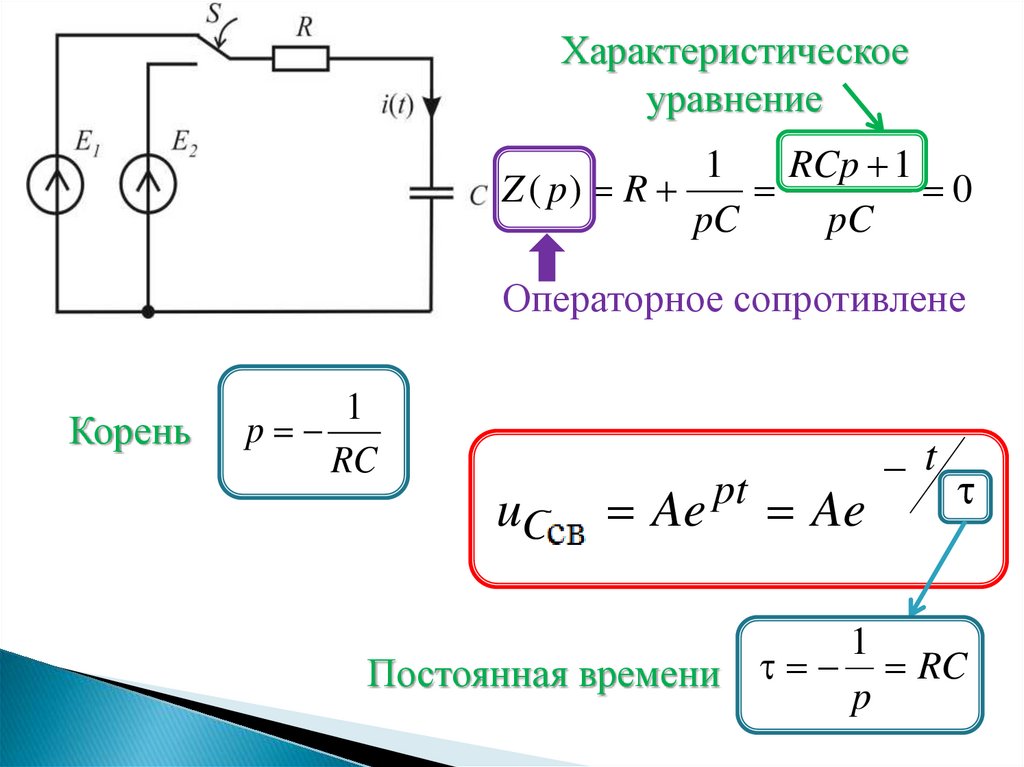
29.
Характеристическоеуравнение
1
RCp 1
Z ( p) R
0
pC
pC
Операторное сопротивлене
Корень
1
p
RC
uCсс Ae
pt
Ae
t
1
Постоянная времени RC
p
30.
4) Установившийся режим t=.
uС пр = Е2.
5) Общее решение ДУ
uС (t) = uС св + uС пр = Ae
6)
uС (0+) = А+ E2 = Е1
t
+ E2.
А Е1 E2
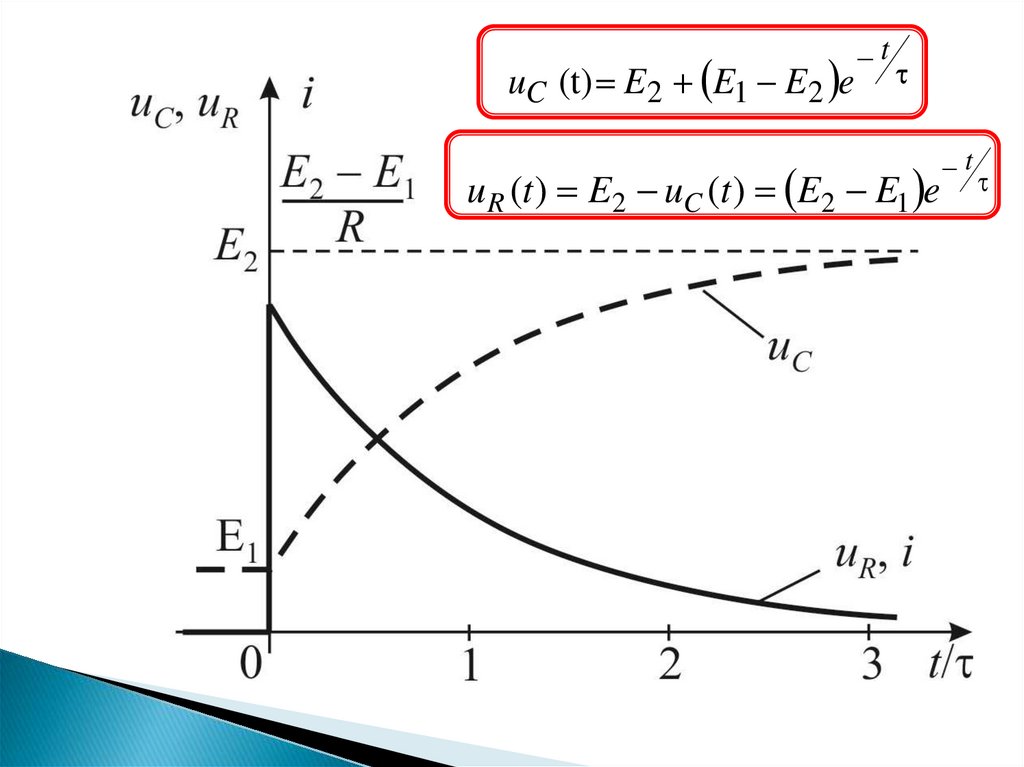
uC (t) E2 E1 E2 e
t
31.
uC (t) E2 E1 E2 et
u R (t ) E2 uC (t ) E2 E1 e
t
32.
ПриЕ2 = 0
uC (t) E1e
t
u R (t ) 0 uC (t ) E1e
t


























 Физика
Физика








