Уравнения Лагранжа II рода. Занятие №3

1. Уравнения Лагранжа II рода

Занятие №3

2.

• Пусть имеется механическая система, имеющая N степеней
свободы. Тогда ее состояние в любой момент времени можно
определить N соответствующим образом выбранными
независимыми параметрами q1, …, qN. Эти параметры
называются обобщенными координатами системы.
• С помощью этих обобщенных координат можно преобразовать
общее уравнение динамики; в результате преобразований
получается система дифференциальных уравнений вида
d T T
Qi
dt qi qi
(i = 1, 2, …, N)
• Величина Т – кинетическая энергия системы. Она должна
быть представлена формулой вида:
T T t , qi , qi
(i = 1, 2, …, N)
• Величина Qi – обобщенная сила, действующая вдоль
координаты qi.

3.

• В результате подстановки и последующих преобразований
получается система обыкновенных дифференциальных
уравнений II порядка для обобщенных координат qi. Решая эту
систему, определяют зависимость всех обобщенных координат
от времени, а значит – состояние всей системы в любой момент
времени.
• Для определения обобщенной силы используется понятие
работы внешних сил на виртуальном перемещении системы.
1. Необходимо определить все внешние силы, действующие на
систему.
2. Дать системе виртуальное перемещение вдоль обобщенной
координаты qi.
3. Необходимо на этом перемещении определить работу всех
внешних сил Аi.
4. Последнее – представить работу в следующем виде:
Ai Qi qi
Коэффициент при вариации обобщенной координаты qi и будет
обобщенной силой Qi.

4.

В случае потенциальных внешних сил
U
Qi
qi
(U – потенциал силы)
Уравнение Лагранжа II рода в этом случае принимает вид:
d L L
0
dt qi qi
Величина L = T + U – кинетический потенциал (функция
Лагранжа).

5. Примеры решения задач

6. Задача №1

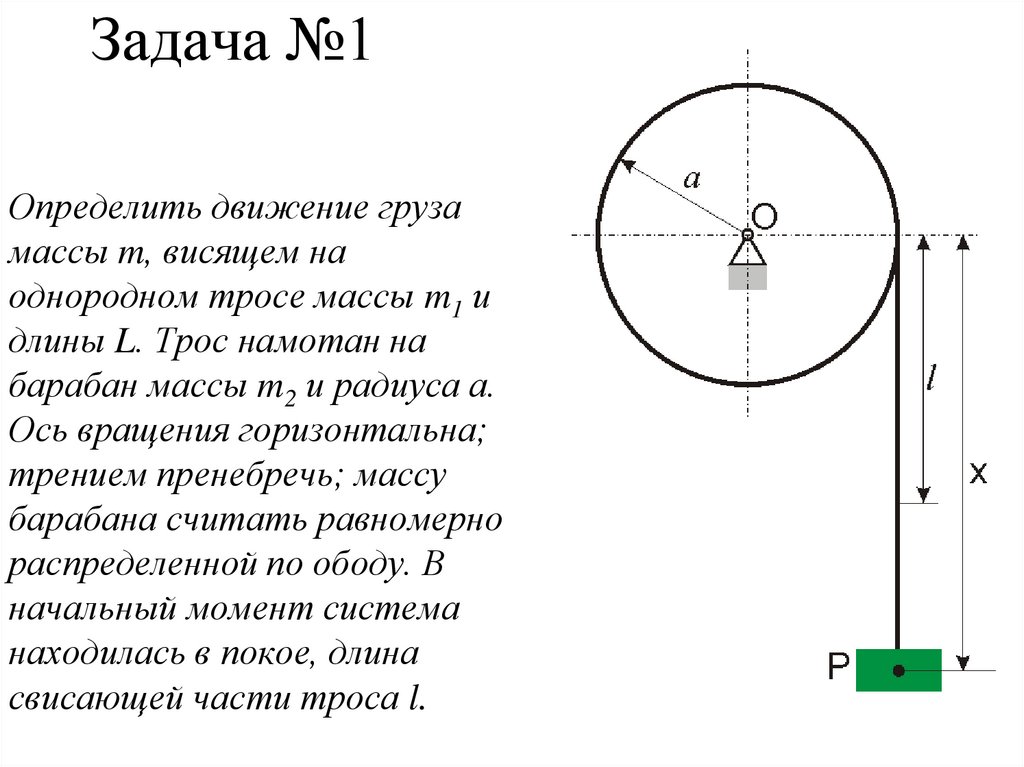
Определить движение груза
массы m, висящем на
однородном тросе массы m1 и
длины L. Трос намотан на
барабан массы m2 и радиуса а.
Ось вращения горизонтальна;
трением пренебречь; массу
барабана считать равномерно
распределенной по ободу. В
начальный момент система
находилась в покое, длина
свисающей части троса l.

7.

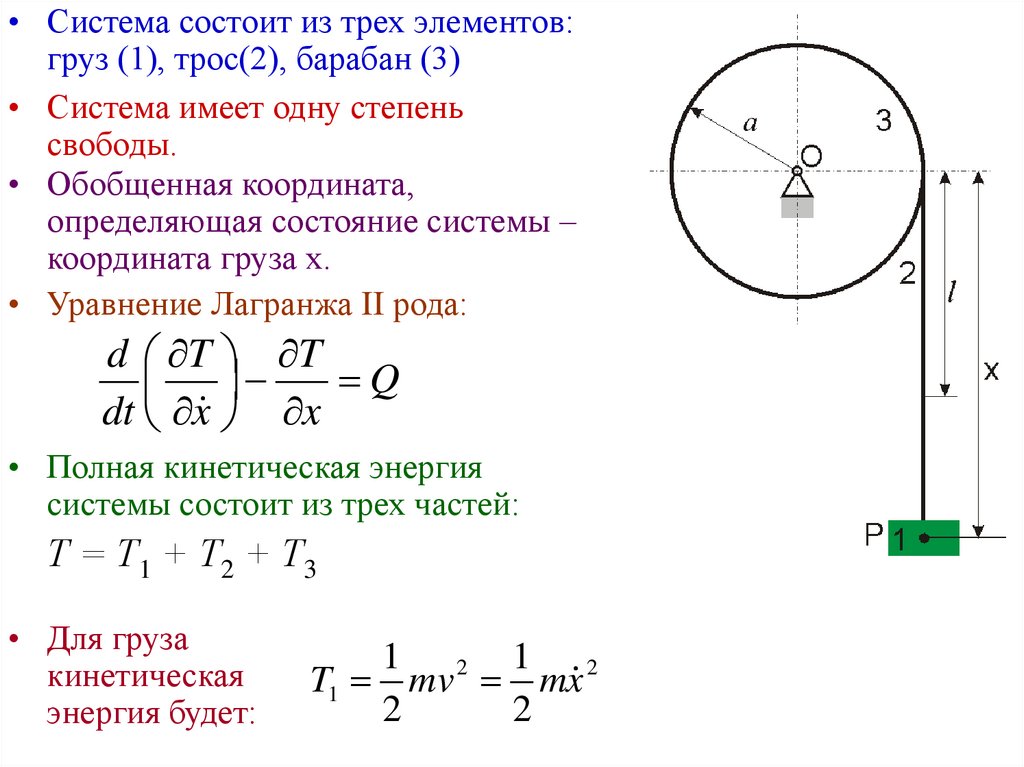
• Система состоит из трех элементов:
груз (1), трос(2), барабан (3)
• Система имеет одну степень
свободы.
• Обобщенная координата,
определяющая состояние системы –
координата груза х.
• Уравнение Лагранжа II рода:
d T T
Q
dt x x
• Полная кинетическая энергия
системы состоит из трех частей:
Т = Т1 + Т2 + Т 3
• Для груза
кинетическая
энергия будет:
1 2 1 2
T1 mv mx
2
2

8.

• Так как все точки троса двигаются со
скоростью, равной скорости груза, то
1
1
2
T2 m1v m1 x 2
2
2
1
• Кинетическая энергия барабана T3 I 2
2
2
Момент инерции I m2 a
v
Угловая скорость
a
После
2
подстановки
1
1
1
2 v
2
T3 m2 a m2 v m2 x 2
2
2
2
a
• Окончательное выражение для кинетической
энергии системы
1 2 1
1
1
2
2
T mx m1 x m2 x m m1 m2 x 2
2
2
2
2
• Выражения для производных
x2
T 1
m m1 m2
x 2
x
m m1 m2 x;
T
0
x

9.

• Для определения обобщенной силы
необходимо показать все внешние
силы, действующие
на систему:
вес груза mg вес барабана m2 g
вес намотанной части троса m1 g
вес свисающей части троса m1 g
N
реакция опоры барабана
• Системе дается виртуальное
перемещение.
Как видно из рисунка
A mg x m1 g x m m1 g x
• Согласно правилу, обобщенная
сила – коэффициент при вариации
обобщенной координаты:
x
Q m m1 g m m1 g
L

10. Подстановка в уравнение Лагранжа II рода дает:

d
x
m m1 m2 x 0 m m1 g ;
dt
L
m1 g
m m1 m2 x mg
x;
L
m1 g
m m1 m2 x
x mg.
L
Линейное неоднородное уравнение с постоянными
коэффициентами решается по стандартной схеме: сумма
общего решения однородного уравнения и частного
решения неоднородного уравнения.

11.

1. Общее решение соответствующего однородного уравнения
m1 g
m m1 m2 x
x 0
L
a. Характеристическое уравнение:
m m1 m2 2 m1 g 0;
L
m1 g
12
.
m m1 m2 L
b. Решение
~
x A e t B e t
2. Частное решение неоднородного уравнения ищется в виде
постоянной:
m1 g
mL
x C m m1 m2 C
C mg C
L
m1
*
3. Общее решение исходного уравнения
mL
*
t
t
~
x x x A e B e
m1

12.

Постоянные А и В определяются из начальных условий:
x(0) l ; x (0) 0
t
x A e B e
t
mL
mL
0
0
x(0) A e B e
m1
m1
mL
mL
l A B
A B l
m1
m1
x A e t B e t x(0) A e 0 B e 0
0 A B A B 0
Окончательно
mL
1 mL
A B l
m1 A B l
2
m1
A B 0

13. Подстановка в общее решение приводит к окончательному ответу:

1 mL t t mL mL
mL
x l
l
;
e e
ch( t )
2
m1
m1
m1
m1
m1 g
m m1 m2 L

14. Задача №2

Составить уравнение
движения маятника,
состоящего из
материальной точки
массы m, подвешенной на
нити, длина которой
изменяется по
произвольно заданному
закону l = l(t)

15.

• В систему входит только один элемент, имеющий массу и
скорость - груз
• Система имеет одну степень свободы (изменение длины нити
происходит по заданному закону и степенью свободы не
является).
• Обобщенная координата, определяющая состояние системы –
угол отклонения нити с грузом от вертикали .
• Уравнение Лагранжа II рода:
d T T
Q
dt
• Для груза кинетическая энергия будет:
1 2
T1 mv
2

16.

• На рисунке видно, что полная скорость груза
складывается из двух перпендикулярных
компонент:
V1 – продольная (вызвана изменением длины
нити)
V2 – окружная (вызвана поворотом нити)
• Их модули равны:
v1 l ; v2 l
• Квадрат модуля полной скорости
v v v l
2
2
1
2
2
2
l l 2 l 2 2
2
• Кинетическая энергия груза
и ее производные:
1
T m l 2 l 2 2
2
T
T
2
m l ;
0

17.

• Для определения обобщенной силы
необходимо показать все внешние силы,
действующие
на систему:
вес груза mg
• Системе дается виртуальное перемещение,
перемещение груза х, его модуль равен
х = l
Как видно из рисунка
A mg x mg x cos 90
0
mg l sin
• Согласно правилу, обобщенная сила – коэффициент при
вариации обобщенной координаты:
Q mg l sin

18.

Подстановка в уравнение Лагранжа II рода дает:
d
2
m
l
0 mgl sin ;
dt
d 2
l gl sin ;
dt
2
l 2l l gl sin ;
l
2 g sin 0.
l

19. Задача №3

Призма B массы m скользит по гладкой боковой
грани призмы A массы М, образующей угол с
горизонтом. Определить ускорение призмы A.
Трением между призмой A и горизонтальной
плоскостью пренебречь.

20.

21.

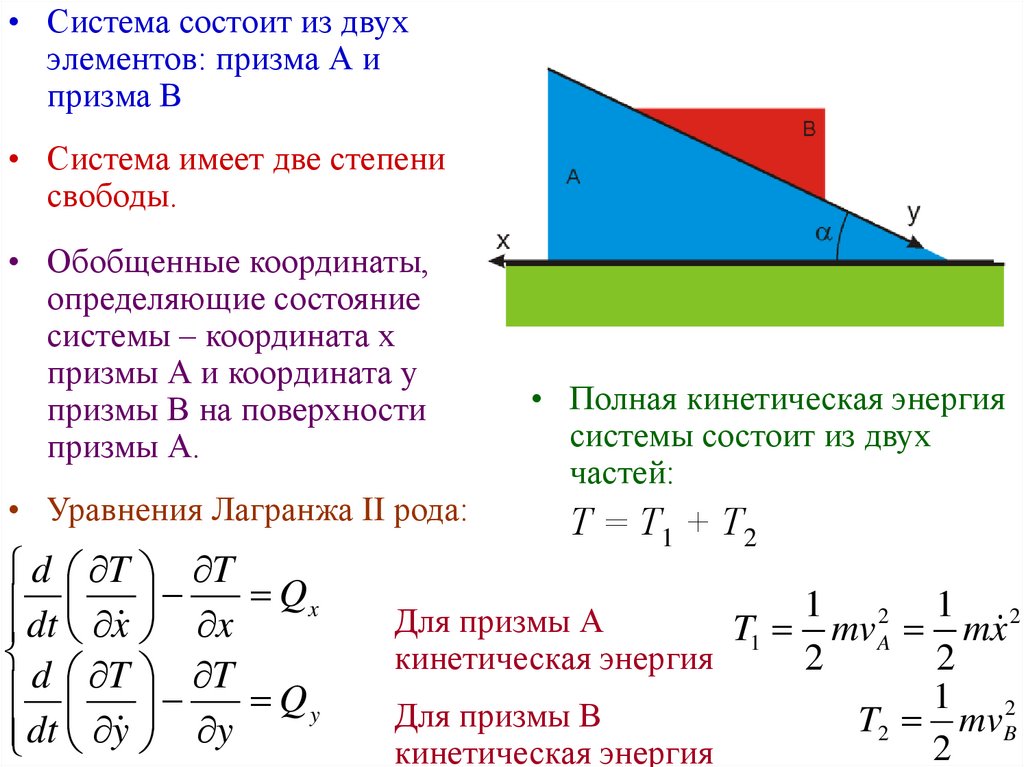
• Система состоит из двух
элементов: призма А и
призма В
• Система имеет две степени
свободы.
• Обобщенные координаты,
определяющие состояние
системы – координата х
призмы А и координата у
призмы В на поверхности
призмы А.
• Уравнения Лагранжа II рода:
d T T
dt x x Qx
d T T Q y
dt y y
• Полная кинетическая энергия
системы состоит из двух
частей:
Т = Т1 + Т 2
1 2 1 2
Для призмы А
T1 mv A mx
кинетическая энергия
2
2
Для призмы В
кинетическая энергия
1 2
T2 mvB
2

22.

Из условия задачи следует,
что призма В совершает
сложное движение: вместе с
призмой А и относительно
призмы
А. Поэтому
vB v A vr
Величины скоростей
v A x ; vr y
По теореме косинусов
2
2
v v v 2 v A vr cos x y 2 x y cos
2
B
2
A
2
r
Окончательное выражение для кинетической энергии системы
1
1
2
T Mx m x 2 y 2 2 x y cos
2
2
T
Mx m x y cos ;
Выражения для
x
производных
T
m y x cos ;
y
T
0
x
T
0
y

23.

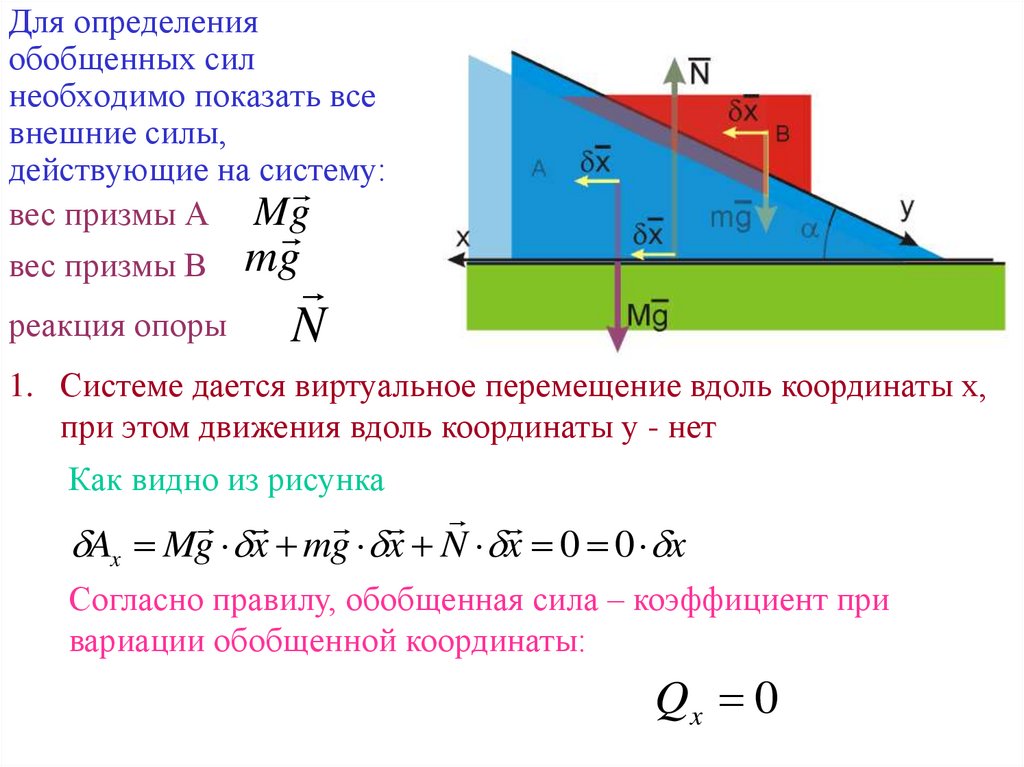
Для определения
обобщенных сил
необходимо показать все
внешние силы,
действующие на систему:
вес призмы А M g
вес призмы В mg
реакция опоры
N
1. Системе дается виртуальное перемещение вдоль координаты х,
при этом движения вдоль координаты у - нет
Как видно из рисунка
Ax Mg x mg x N x 0 0 x
Согласно правилу, обобщенная сила – коэффициент при
вариации обобщенной координаты:
Qx 0

24.

2. Системе дается виртуальное перемещение вдоль координаты у,
при этом движения вдоль координаты х - нет
Как видно из рисунка
Ay mg y mg y cos 900 mg sin y
Согласно правилу, обобщенная сила – коэффициент при
вариации обобщенной координаты:
Q y mg sin

25.

Подстановка в систему уравнений Лагранжа приводит к следующей
системе уравнений:
d
dt Mx m x y cos 0 0
d m y x cos 0 mg sin
dt
Mx m x y cos 0
M m x m cos y 0
m y x cos mg sin
y x cos g sin
Искомое неизвестное – ускорение призмы А:
y x cos g sin
M m x m cos x cos g sin 0
M m m cos 2 x mg sin cos
mg sin cos
mg sin 2
x
2
2
M
m
m
c
os
2
M
m
si
n

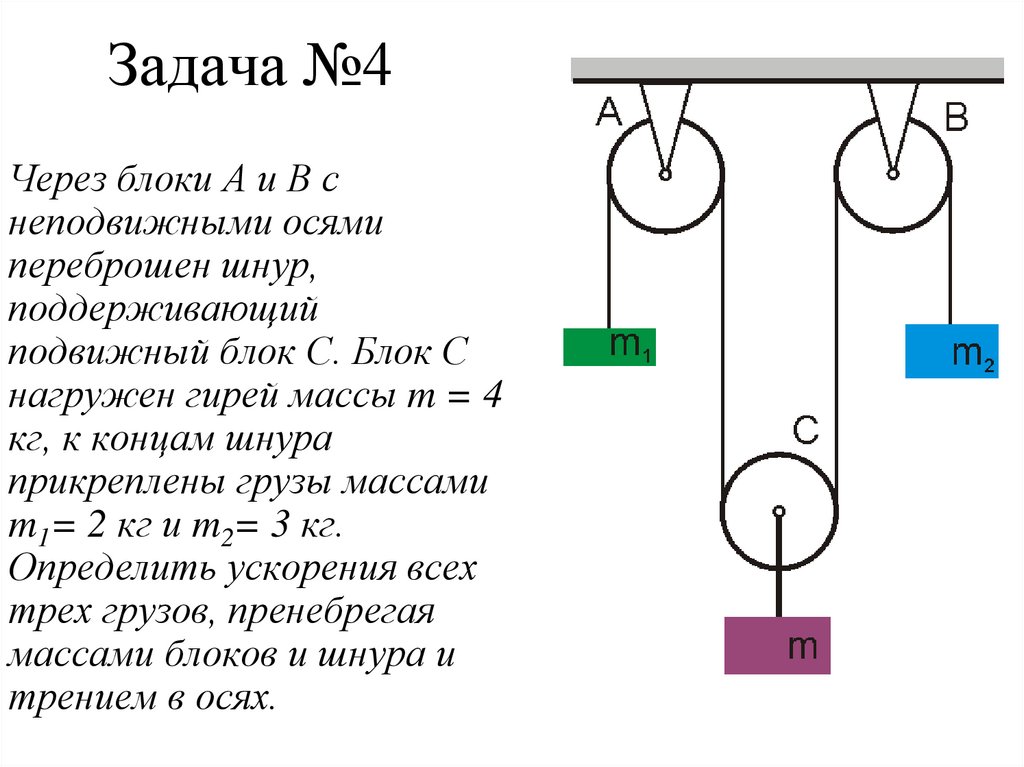
26. Задача №4

Через блоки А и В с
неподвижными осями
переброшен шнур,
поддерживающий
подвижный блок С. Блок С
нагружен гирей массы m = 4
кг, к концам шнура
прикреплены грузы массами
m1= 2 кг и m2= 3 кг.
Определить ускорения всех
трех грузов, пренебрегая
массами блоков и шнура и
трением в осях.

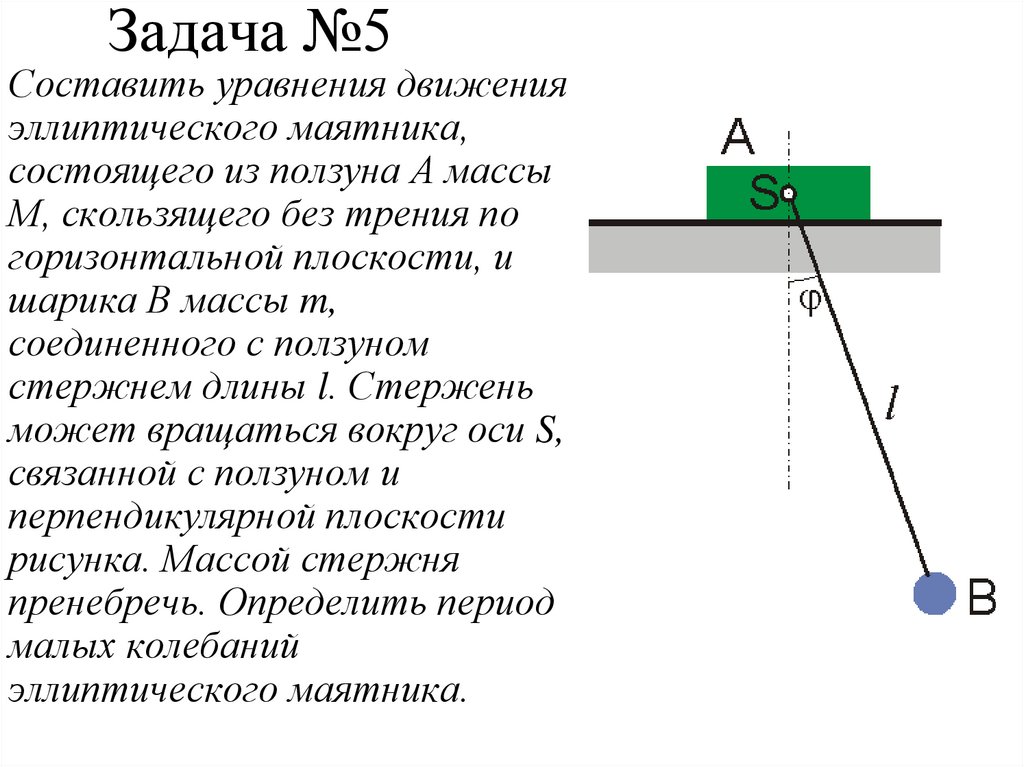
27. Задача №5

Составить уравнения движения
эллиптического маятника,
состоящего из ползуна А массы
М, скользящего без трения по
горизонтальной плоскости, и
шарика В массы m,
соединенного с ползуном
стержнем длины l. Стержень
может вращаться вокруг оси S,
связанной с ползуном и
перпендикулярной плоскости
рисунка. Массой стержня
пренебречь. Определить период
малых колебаний
эллиптического маятника.

28.

29.

• Система состоит из двух
элементов: ползун А и груз В
• Система имеет две степени
свободы.
• Обобщенные координаты,
определяющие состояние
системы – координата х
ползуна А и угол отклонения
маятника В от вертикали
• Уравнения Лагранжа II рода:
• Полная кинетическая энергия
системы состоит из двух
частей:
Т = Т1 + Т 2
d T T
1
1
2
2
Q
x
dt x
T
Mv
M
x
Для ползуна А
1
A
x
2
2
кинетическая энергия:
1 2
d T T Q Для груза В
T2 mvB
dt
2
кинетическая энергия

30.

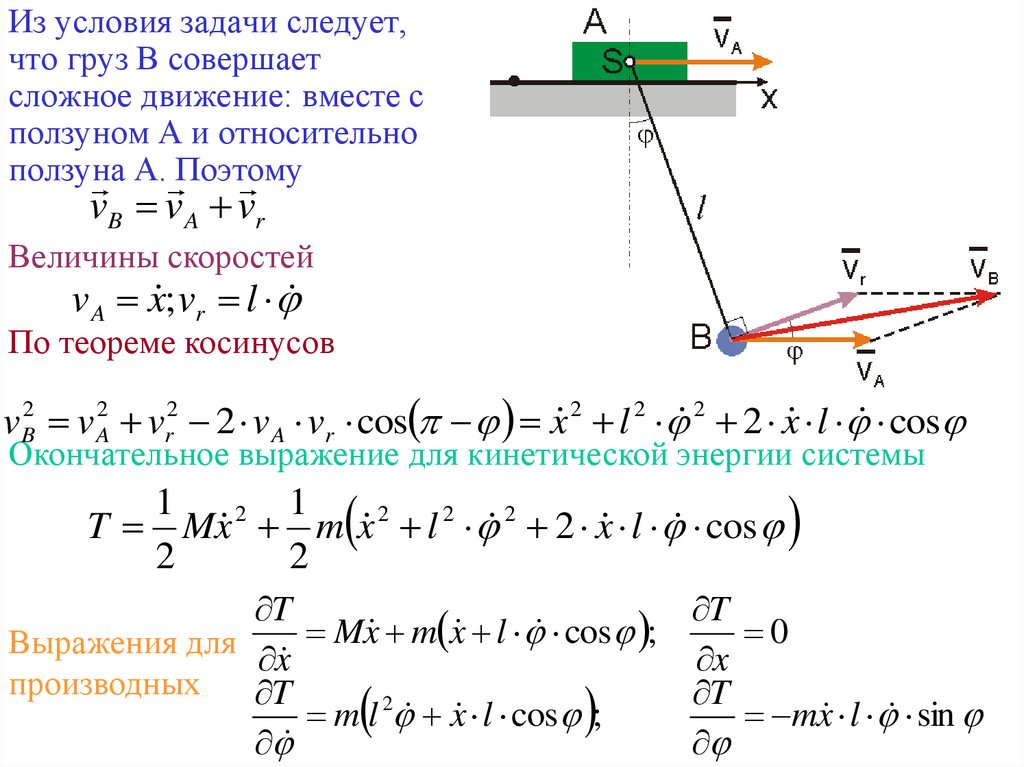
Из условия задачи следует,
что груз В совершает
сложное движение: вместе с
ползуном А и относительно
ползуна
А. Поэтому
vB v A vr
Величины скоростей
v A x ; vr l
По теореме косинусов
vB2 v A2 vr2 2 v A vr cos x 2 l 2 2 2 x l cos
Окончательное выражение для кинетической энергии системы
1
1
2
T Mx m x 2 l 2 2 2 x l cos
2
2
T
T
M
x
m
x
l
cos
;
0
Выражения для
x
x
производных
T
T
2
m l x l cos ;
mx l sin

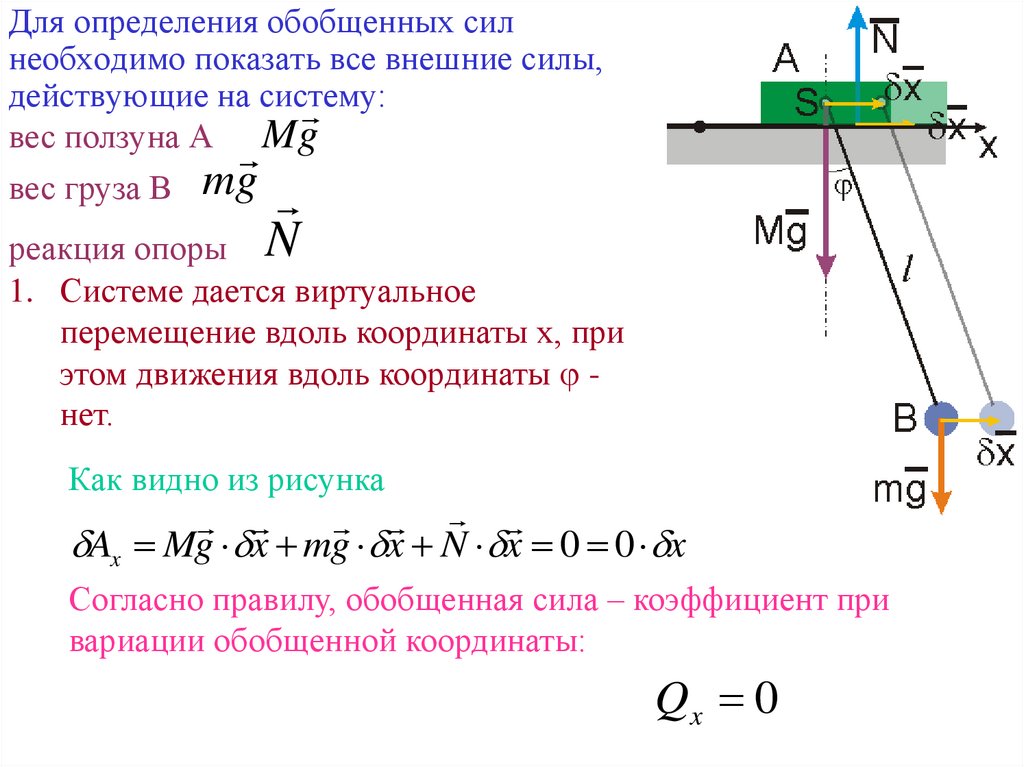
31.

Для определения обобщенных сил
необходимо показать все внешние силы,
действующие на систему:
вес ползуна А Mg
вес груза В mg
реакция опоры N
1. Системе дается виртуальное
перемещение вдоль координаты х, при
этом движения вдоль координаты нет.
Как видно из рисунка
Ax Mg x mg x N x 0 0 x
Согласно правилу, обобщенная сила – коэффициент при
вариации обобщенной координаты:
Qx 0

32.

2. Системе дается виртуальное
перемещение вдоль координаты ,
при этом движения вдоль
координаты х - нет
Как видно из рисунка
Ay mg y mg y cos 900 mg sin l
Согласно правилу, обобщенная сила – коэффициент при
вариации обобщенной координаты:
Q mgl sin

33.

Подстановка в систему уравнений Лагранжа приводит к следующей
системе уравнений:
d
dt Mx m x l cos 0 0
d
m l 2 x l cos mx l sin mgl sin
dt
M x m x l cos sin 0
ml l x cos x sin mx l sin mgl sin
M m x ml cos 2 sin 0
l x cos g sin 0
Эти уравнения и являются уравнениями движения эллиптического
маятника
Аналитического решения данная система не имеет. Однако в случае
малых колебаний ее можно существенно упростить.

34.

При малых колебаниях можно отбросить все произведения,
содержащие обобщенные координаты и их производные в степени
выше первой, а также воспользоваться приближениями:
cos 1; sin
Тогда система уравнений примет следующий вид:
M m x ml 0
l x g 0
Полученную систему можно преобразовать:
ml
ml
x
l
g 0
M m
M m
Ml
g M m
g 0
0
M m
l
M
Последнее равенство совпадает с
2 0
уравнением колебаний:
Отсюда легко получается
формула для периода
малых колебаний
g M m 2
l
M
TK 2
l
M
TK
g M m