Потенциальное векторное поле. Лекция 3

1. Лекция 3. Потенциальное векторное поле

2013

2.

Работа сил поля по перемещению заряда
(энергетическая характеристика поля)
Из механики: любое потенциальное поле центральных сил является
консервативным. Работа сил такого поля зависит не от пути, а только
от начального и конечного положения тел.
2
2
A Fdl qEdl q Edl q El dl
l
l
1
1
Сходство законов всемирного тяготения и Кулона позволяет
предположить, что и электростатические силы консервативные
Работа силы по замкнутому контуру:
A q Edl 0
Edl циркуляция E
El E cos проекция E на направление перемещения
L
L
В противном случае был бы вечный двигатель
2
2

3.

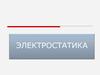
Теорема о циркуляции вектора E
Циркуляция
вектора
напряженности
любого
электростатического поля всегда равна нулю
Edl 0
Доказательство:
2 1 2 2
Edl Edl Edl 0
1
2
1
1
Следствия из теоремы о циркуляции:
1. Линии напряженности поля
не могут быть замкнуты
2. Невозможна представленная
конфигурация поля
3
3

4.

Потенциал электрического поля
Работа А, совершаемая силами электростатического поля
при перенесении заряда q, равна убыли потенциальной
энергии этого заряда dA = - dW
2
A q Edl W1 W2
1
W1, W2 – потенциальная энергия заряда в точках 1 и 2.
Потенциал электрического поля: энергетическая характеристика
электрического поля; скалярная величина, численно равная
потенциальной энергии единичного положительного заряда в данной
точке поля.
W [ ] В
q (вольт)
Разность потенциалов между двумя
точками равна одному вольту (СИ), если для
перемещения между ними одного кулона эл-ва
нужно совершить работу, равную одному джоулю.
A q( 1 2 ),
4
( 1 2 )
-разность потенциалов
4

5.

Потенциал электрического поля
2
Edl 1 2
1
Потенциал электрического поля определяется с
точностью до аддитивной постоянной. Потенциал
точки поля численно равен работе по перемещению
точечного положительного заряда из бесконечности в
данную точку поля:
A
A q( ) q
q
Потенциал на бесконечности равен нулю:
0
5
5

6.

Взаимосвязь напряженности и потенциала
2
Edl 1 2
1
Для элементарных перемещений dl:
Edl El dl d
В проекциях на координатные оси:
Ex ; E y ; Ez
x
y
z
E i
j k grad
y
z
x
Напряженность в некой точке Е-поля равна градиенту
потенциала в этой точке, взятому с обратным знаком.
Через оператор набла естественным способом выражаются
основные операции векторного анализа: grad (градиент), div
(дивергенция), rot (ротор)
6
6

7.

Взаимосвязь напряженности и потенциала
для однородного поля (E=const)
1 2 El cos
α – угол между направлением перемещения и
линиями напряженности электрического поля.
7
7

8.

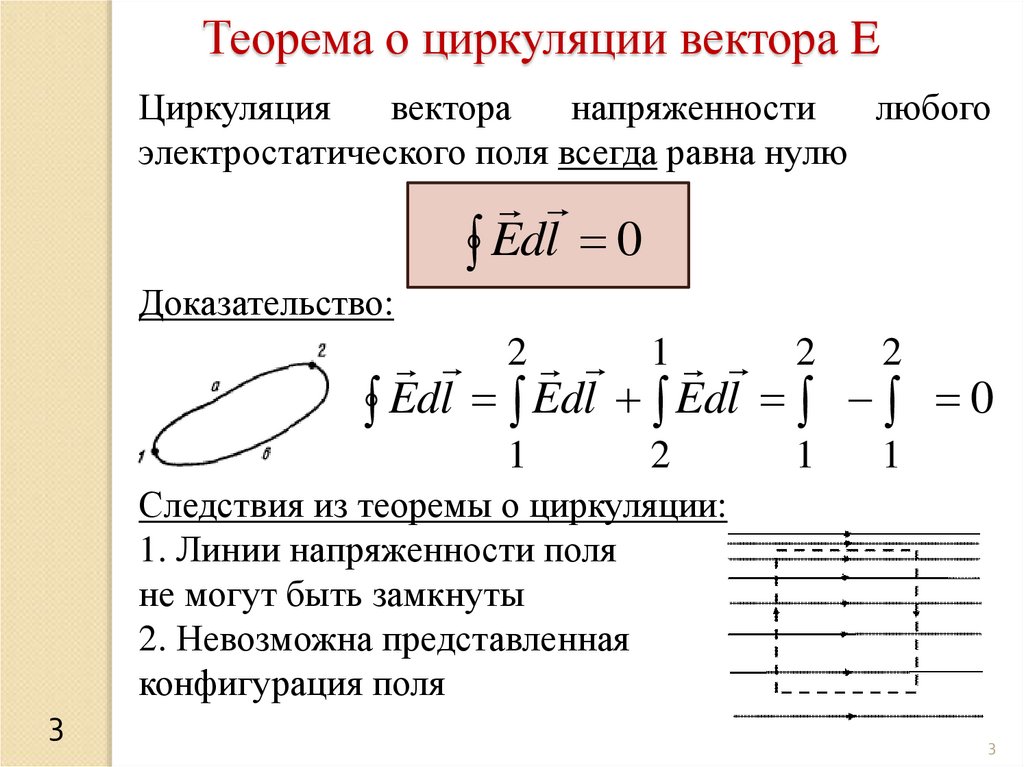
Потенциал точечного заряда
Напряженность поля точечного заряда:
E
kq
r
2
kq
2
kq
Edl dr
2
r r
1
rr
kq kq kq
r
r
kq
r
8
8

9.

Потенциал системы зарядов
Принцип суперпозиции для вектора напряженности:
E E1 E2 ... En
Принцип суперпозиции для потенциала системы
зарядов:
1 2 ... n
Непрерывное распределение зарядов:
1
1
1
dl
dS
dV
4 0
4 0
4 0
9
9

10.

Потенциал поля, создаваемого различными
заряженными телами
1. Бесконечная равномерно заряженная плоскость с
поверхностной плотностью σ.
E
const
2 0
U 1 2 El cos
l cos
2 0
2. Потенциал электрического поля цилиндра (нити)
радиусом R, равномерно заряженного с линейной
плотностью τ.
2
2 1
r2
ln
U El dl
dr
2 0
r1
1
1 2 0 r
10
10

11.

Потенциал поля, создаваемого различными
заряженными телами
3.
11
Потенциал электрического поля равномерно
заряженной сферы радиусом R с зарядом Q
11

12.

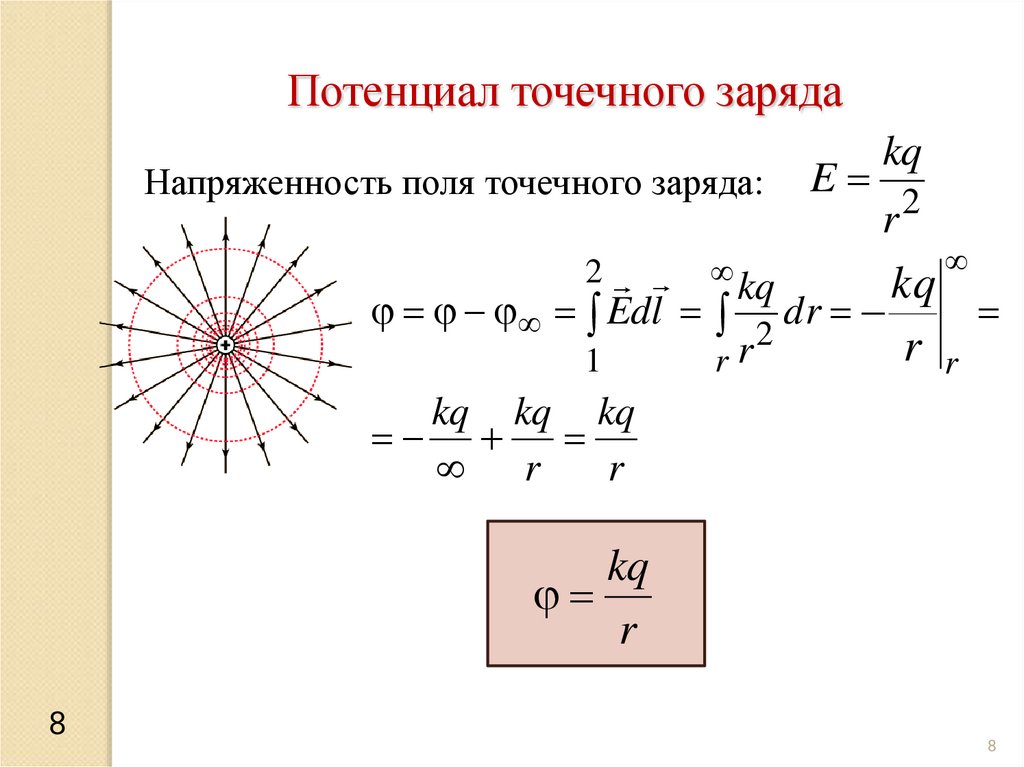
Эквипотенциальные поверхности
- поверхности, в каждой точке которых потенциал имеет
одно и тоже значение.
Свойства эквипотенциальных поверхностей:
1. Линии напряженности всегда
перпендикулярны эквипотенциальным
поверхностям.
2. Густота эквипотенциальных
поверхностей пропорциональна напряженности поля.
3.
Работа
по
перемещению
заряда
вдоль
эквипотенциальной поверхности равна нулю.
A q( 1 2 ) 0
12
12

13.

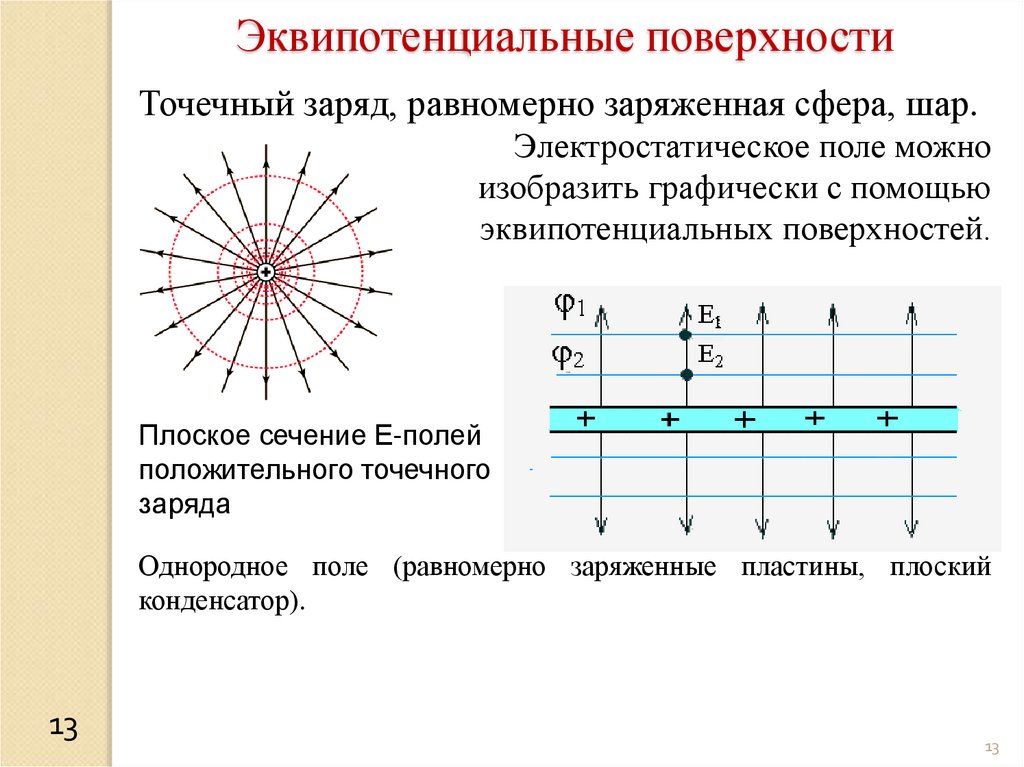
Эквипотенциальные поверхности
Точечный заряд, равномерно заряженная сфера, шар.
Электростатическое поле можно
изобразить графически с помощью
эквипотенциальных поверхностей.
Плоское сечение Е-полей
положительного точечного
заряда
Однородное поле (равномерно заряженные пластины, плоский
конденсатор).
13
13

14.

Энергия взаимодействия системы зарядов
Система из n точечных зарядов.
Работа всех сил
взаимодействия произвольной
системы зарядов равна убыли
энергии взаимодействия зарядов этой системы:
dA dW
Найдем выражение для энергии взаимодействия W:
W W12 W13 W23 ...
14
Энергия взаимодействия пары зарядов
1
W12 W12 W21
2
14

15.

Энергия взаимодействия системы зарядов
Для n зарядов:
1
W (W12 W13 ... W1n ) (W22 W23 ... W2n ) ...
2
В каждой скобке – энергия взаимодействия i–го
заряда со всеми остальными.
1 n
W Wi
2 i 1
Учитывая что W q ,
получаем
1 n
W qi i
2 i 1
i - потенциал, создаваемый всеми зарядами
15
системы кроме в месте его нахождения.
15

16.

Энергия взаимодействия системы зарядов
Энергия взаимодействия пары зарядов
Заряды qi находятся на расстоянии r друг от друга.
Найдем энергию взаимодействия q1 и q2
1
1
kq2
kq1
W (q1 1 q2 2 ) (q1
q2
)
2
2
r
r
kq1q2
kq1q2
W
r
r
С точки зрения современной физики все электрические явления
сводятся к изменениям полей зарядов в пространстве с конечной
скоростью, равной скорости света.
16
16