Похожие презентации:
Циркуляция вектора напряженности. Расчеты потенциальных полей. (Лекция 15)
1.
ЭЛЕКТРОСТАТИКАЛекция 15.
Тема: Циркуляция вектора напряженности.
Расчеты потенциальных полей.
Учебник:
Трофимова Т.И. Курс физики : учеб. пособ. для вузов / Т. И.
Трофимова. - М.: Академия, 2007.- с. 155-160.
к.ф.-м.н.
Курочкин А.Р.
2.
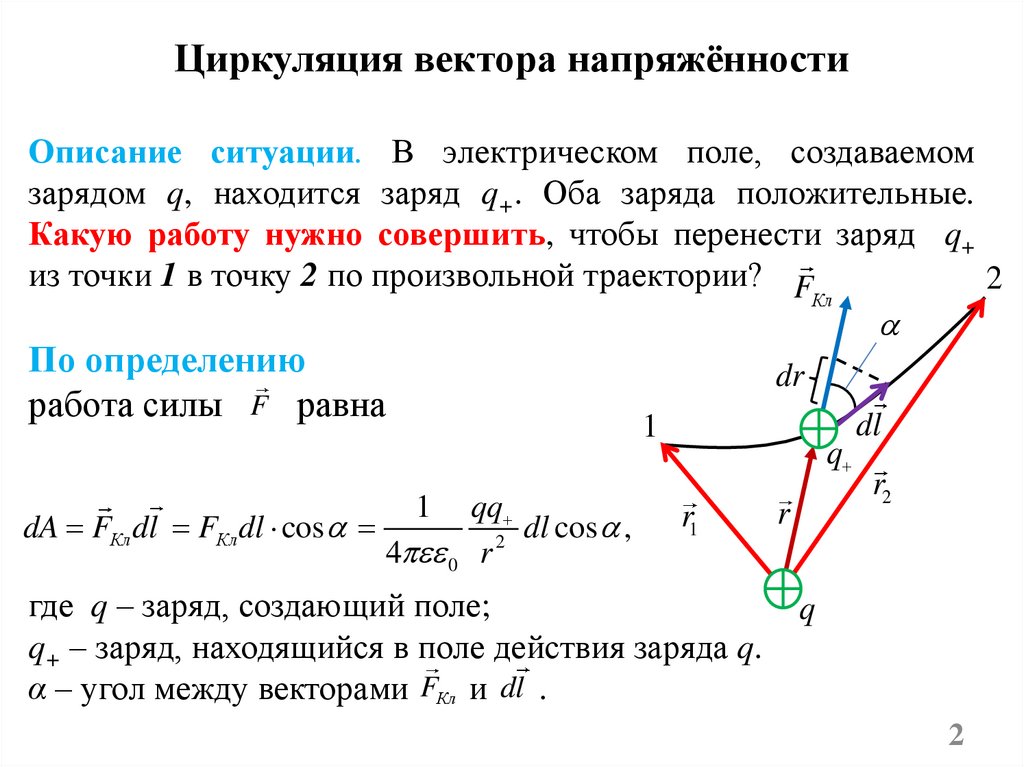
Циркуляция вектора напряжённостиОписание ситуации. В электрическом поле, создаваемом
зарядом q, находится заряд q+. Оба заряда положительные.
Какую работу нужно совершить, чтобы перенести заряд q+
из точки 1 в точку 2 по произвольной траектории? F
2
Кл
По определению
dr
работа силы F равна
dl
1
q
r2
1 qq
r
r1
dA FКл dl FКл dl cos
dl
cos
,
4 0 r 2
где q – заряд, создающий поле;
q+ – заряд, находящийся в поле действия заряда q.
α – угол между векторами FКл и dl .
q
2
3.
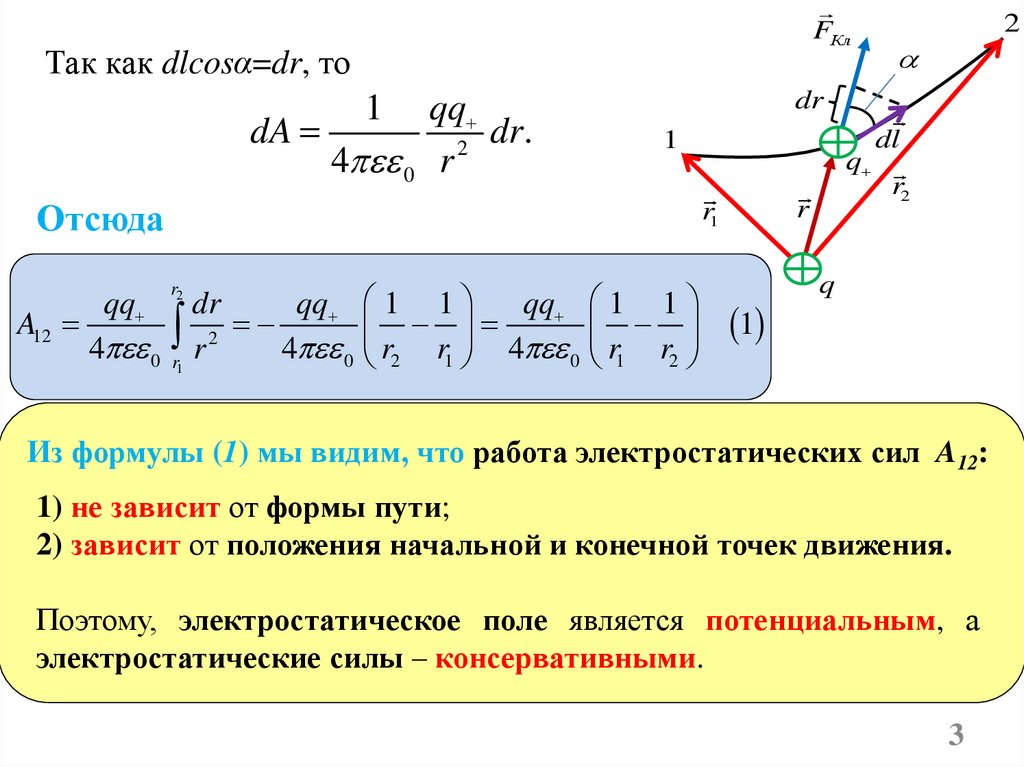
FКлТак как dlcosα=dr, то
dA
dr.
2
4 0 r
dr
1
1
Отсюда
q
r
r1
qq dr
qq 1 1
qq 1 1
A12
2
4 0 r1 r
4 0 r2 r1 4 0 r1 r2
r2
2
1
dl
r2
q
Из формулы (1) мы видим, что работа электростатических сил A12:
1) не зависит от формы пути;
2) зависит от положения начальной и конечной точек движения.
Поэтому, электростатическое поле является потенциальным, а
электростатические силы – консервативными.
3
4.
3) будет равна нулю при перемещении электрического заряда вовнешнем электростатическом поле по любому замкнутому пути L
(является следствием потенциальности электростатического поля).
dA 0 2
L
т.к.
F
dA F dl E
F q E q E dl ,
q
то в соответствии с утверждением (2)
q E dl
q E dl 0.
L
Поэтому
L
E dl 0
L
4
5.
Таким образом,Edl
0.
3
L
Интеграл (3) называется циркуляцией вектора напряжённости.
Теорема о циркуляции вектора напряжённости
электростатического поля
Циркуляция вектора напряжённости электростатического поля
вдоль любого замкнутого контура равна нулю.
Важно!
Любое силовое поле, обладающее свойством
называется потенциальным.
Edl
0,
L
5
6.
Освежим воспоминания из раздела «Механика».Вопрос №1. Что называется потенциальной энергией?
Ответ. Потенциальная энергия Ep – СФВ, являющаяся мерой
взаимодействия тел или частей тела и зависящая от расстояния
между ними.
Если в системе действуют потенциальные силы, то может быть
определена некоторая функция координат взаимодействующих тел
Ep (x,y,z), которая называется потенциальной энергией системы.
Вопрос №2. Как формулируется теорема о потенциальной энергии?
Ответ. Убыль потенциальной энергии взаимодействия тел равна
работе всех консервативных сил, действующих на тела системы в
процессе перехода из начального состояния в конечное.
n
E p1 E p 2 E Aiконс
i 1
4
6
7.
Вопрос №3. В чем особенность потенциальной энергии, чтоотличает её от кинетической энергии?
Ответ.
1) Потенциальная энергия определяется с точностью до
произвольной постоянной С, значение которой зависит от выбора
нулевого уровня потенциальной энергии.
2) Потенциальная энергия может иметь как положительное, так и
отрицательное числовое значение.
Согласно уравнению (1)
qq 1 1
A12
.
4 0 r1 r2
Отсюда, с учётом уравнения (4)
A12
4 0 r1
4 0 r2
E p1 E p 2 .
5
7
8.
Следовательно, потенциальная энергия взаимодействия двух точечныхзарядов определяется выражением:
Ep
4 0 r
C.
6
Важно!
1) Значение постоянной С зависит от выбора нулевого уровня
потенциальной энергии.
2) Заряды, находящиеся на бесконечно большом расстоянии, не
взаимодействуют, поэтому при r→∞ Ep(r→∞)=0, откуда С=0. В этом
случае
Ep
4 0 r
.
7
3) Потенциальная энергия взаимодействия одноименных зарядов
(энергия отталкивания) положительна, а разноименных (энергия
притяжения) – отрицательна. По мере уменьшения взаимного
расстояния энергия взаимодействия (7) растет по модулю.
8
9.
Новый вопрос. Как определить потенциальную энергию заряда q0,находящегося в поле n зарядов?
Ответ. Если поле создаётся системой n точечных зарядов q1, q2,…, qn,
то работа электростатических сил, совершаемая над зарядом q0, равна
алгебраической сумме работ сил, обусловленных каждым из зарядов в
отдельности. Поэтому потенциальная энергия Ep заряда q0,
находящегося в этом поле, равна сумме потенциальных энергий Epi,
каждого из зарядов:
n
n
E p E pi q0
i 1
i 1
qi
4 0 ri
.
8
9
10.
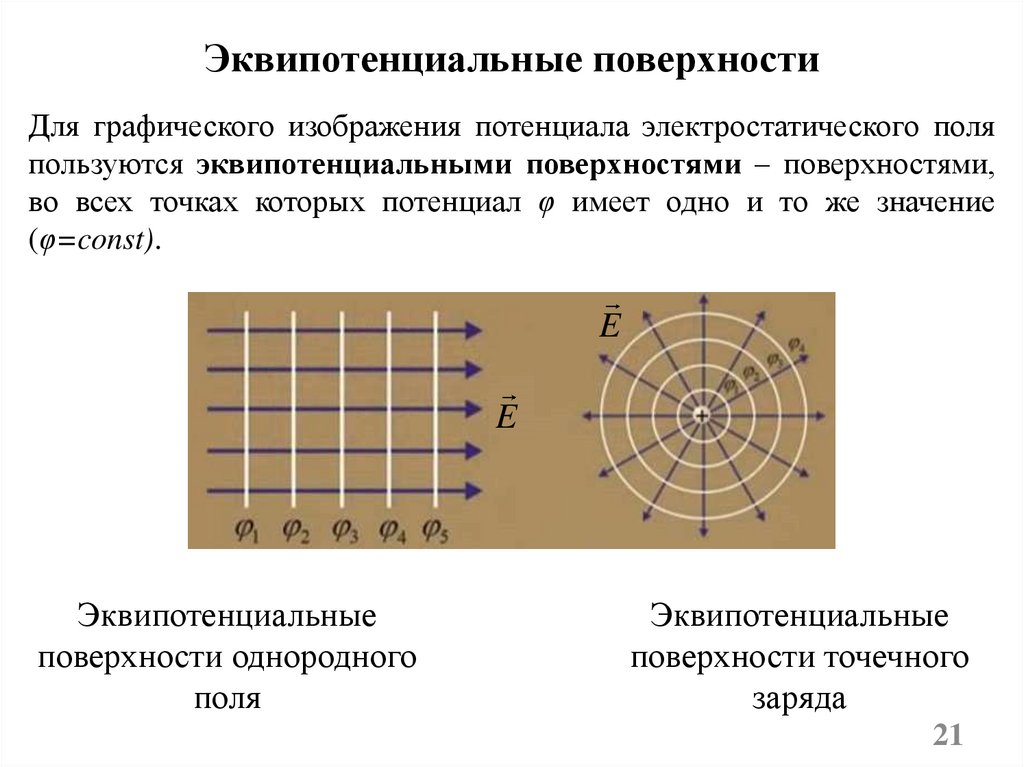
Потенциал φ электрического поляДля характеристики полей удобно ввести в рассмотрение
энергетическую характеристику – потенциал.
Обсудим уравнение*:
q
q – заряд, создающий поле;
r – расстояние от этого заряда до той точки
поля A, в которой помещён пробный заряд q+.
*E p
4 0 r
r
A
q+
C.
Различные пробные заряды q1, q2, … будут обладать в т. А
различной потенциальной энергией.
Ep
Отношение q не зависит от величины пробного заряда q+ и
может
служить
энергетической
характеристикой
электрического поля в данной точке. Эта характеристика
называется потенциалом φ электрического поля.
10
11.
Потенциал электрического поля φ – СФВ, энергетическаяхарактеристика поля, равная потенциальной энергии, которой
обладал бы в данной точке поля единичный положительный заряд.
Ep
q
Дж
В
Кл
.
9
Свойства потенциала.
1) Потенциал – величина алгебраическая (как и заряд q). Может
быть положительной и отрицательной.
2) Числовое значение потенциала зависит от выбора нулевого
уровня φ. Нулевой уровень потенциала – геометрическое место
точек поля, потенциал которых принимается равным нулю.
Выбирается произвольно.
11
12.
Потенциал φ поля точечного зарядаЕсли поле создаётся точечным зарядом q, то пробный заряд q+
обладает в точке A потенциальной энергией (6).
Ep
4 0 r
C.
q
r
A
q+
Следовательно, потенциал электрического поля φ, созданного
точечным зарядом q, в точке A равен:
Ep
q
q
4 0 r
C.
Примем, что φ=0 при r→∞. Тогда С=0 и
1
q
.
4 0 r
10
12
13.
Принцип суперпозиции для потенциалаЕсли поле создано совокупностью точечных зарядов q1, q2, … , qi, … qn ,
то его потенциал в т. А равен алгебраической сумме потенциалов φi
создаваемых в т. А каждым из зарядов qi в отдельности:
A
q1
n
n
qi
i
.
4 0 i 1 ri
i 1
1
11
q2
qi
q3
qn
Пример. Найти результирующий потенциал в точке B.
B
2а
-q
1B 2 B
а +4q
q
1 4q
1 3q 8q
1 5q
4 0 2a 4 0 3a 4 0 6a 4 0 6a
1
13
14.
Энергия взаимодействия системы зарядовN
N
1
1
qi k qi i .
2 i 1 k 1 2 i 1
k i
N
Ep
12
N
i k - суммарный потенциал, создаваемый всеми зарядами,
k 1
кроме qi , в точке, где помещается заряд qi
k i
1
Множитель 2 в (12) появился потому, что в результате суммирования
энергий зарядов все парные взаимодействия оказались учтены
дважды.
14
15.
Пример. Найти энергию взаимодействия системы зарядов.q3
E p
1
q1 2 3 q2 1 3 q3 1 2
2
3
2
1
a
a
q1
q2
a
q3
q3
q2
1 q2
q1
q1
q1 k k q2 k k q3 k k
2 a
a
a
a
a
a
1 q1q2 q1q3 q2 q1 q2 q3 q3q1 q3q2
k
2 a
a a
a a
a
k
q1q2 q1q3 q2 q3
a
15
16.
Работа, совершаемая силами электростатическогополя
С учётом формулы (5)
1 q
1
q
A12
q
4 0 r1 4 0 r2
4 0 r1 4 0 r2
1
2
A12 q 1 2 ,
13
т.е. работа, совершаемая силами электростатического поля
при перемещении заряда q+ из точки 1 в точку 2 равна
произведению
перемещаемого
заряда
на
разность
потенциалов в начальной и конечной точках.
16
17.
Представим (13) в видеA12
1 2
,
q
14
т.е. разность потенциалов между точками 1 и 2 - это скалярная
физическая величина, равная работе сил электростатического поля по
перемещению единичного (q+=1Кл) пробного заряда из точки 1 в
точку 2.
Разность потенциалов между двумя точками равняется 1В, если при
перемещении пробного заряда в 1Кл из одной точки в другую силы
электрического поля совершают работу 1Дж.
Важный нюанс! При решении конкретных задач физический
смысл имеет разность потенциалов между двумя точками
электростатического поля.
17
18.
Напряжённость как градиент потенциалаНеобходимо:
найти
взаимосвязь
между
напряжённостью
электростатического поля – силовой характеристикой поля и
потенциалом – энергетической характеристикой поля.
Мы знаем, что сила электрического взаимодействия является
консервативной. Эта сила взаимосвязана с потенциальной энергией:
dA Fdr dE p
F Fx i Fy j Fz k























 Физика
Физика








